• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 11.1 Class 10 Maths Chapter 11 - Constructions

NCERT Solutions for Exercise 11.1 Class 10 Maths Chapter 11 - Constructions

Edited By Ramraj Saini | Updated on Nov 27, 2023 04:09 PM IST | #CBSE Class 10th
Upcoming Event
CBSE Class 10th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 11 Exercise 11.1

NCERT Solutions for Exercise 11.1 Class 10 Maths Chapter 11 Constructions are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 11.1 enlists a few practice problems on the construction of triangles with given measurements base and heights. In the later section some more questions, terms related to the property of triangles, and how its construction can be made in two-dimensional geometry will be discussed.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 11 Exercise 11.1
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 11 exercise 11.1
  3. Assess NCERT Solutions for Class 10 Maths chapter 11 exercise 11.1
  4. More About NCERT Solutions for Class 10 Maths Chapter 11 Exercise 11.1
  5. Benefits of NCERT Solutions for Class 10 Maths Chapter 11 Exercise 11.1
  6. NCERT Solutions Subject Wise
NCERT Solutions for Exercise 11.1 Class 10 Maths Chapter 11 - Constructions
NCERT Solutions for Exercise 11.1 Class 10 Maths Chapter 11 - Constructions

10th class Maths exercise 11.1 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 11 exercise 11.1

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 11 exercise 11.1

Constructions Class 10 Chapter 11 Exercise: 11.1

In each of the following, give the justification of the construction also:
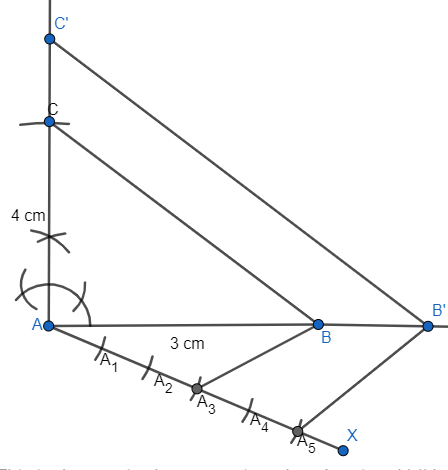
Q1 Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.

Answer:

Steps of construction:-

(i) Draw a line segment AB of measurement 7.6 cm (length).

(ii) Now draw an acute angle AC with line segment AB.

(iii) Now cut 13 equal points on the line AC where the zeroth point is A.

(iv) Join the 13th point with point B. So the new line is BA 13 .

(v) Now, from point A 5 draw a line parallel to BA 13 on line AB. Name the point as D.

The point D is the required point which divides the line segment in the ratio of 5: 8.

The length of the two parts obtained is 2.9 cm and 4.7 cm for AD and DB respectively.


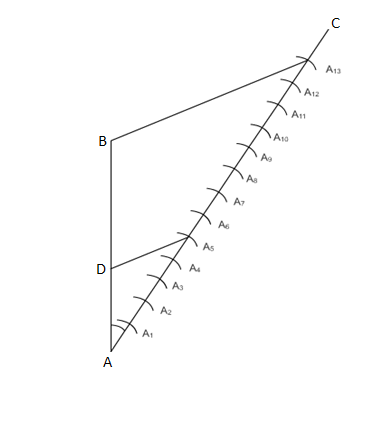
Constructions, 24670

Justification:- In the figure, we can see two similar triangles: \Delta ADA_5 and \Delta ABA_{13}

Thus \frac{AA_5}{A_5A_{13}}\ =\ \frac{AD}{DB}\ =\ \frac{5}{8} .

Q2 Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.

Answer:

Steps of construction are:-

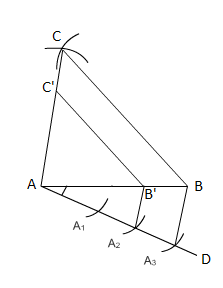
(i) Firstly draw a line segment AB of length 4 cm.

(ii) Now cut an arc of radius 5 cm from point A and an arc of 6 cm from point B.

(iii) Name the point of intersection of arcs to be point C.

(iv) Now join point AC and BC. Thus \Delta ABC is the required triangle.

(v) Draw a line AD which makes an acute angle with AB and is opposite of vertex C.

(vi) Cut three equal parts of line AD namely AA 1 , AA 2 , AA 3 .

(vii) Now join A 3 to B. Draw a line A 2 B' parallel to A 3 B.

(viii) And then draw a line B'C' parallel to BC.

Hence \Delta AB'C' is the required triangle.

1636090329369

Q3 Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are 7 / 5 of the corresponding sides of the first triangle.

Answer:

Steps of construction are:-

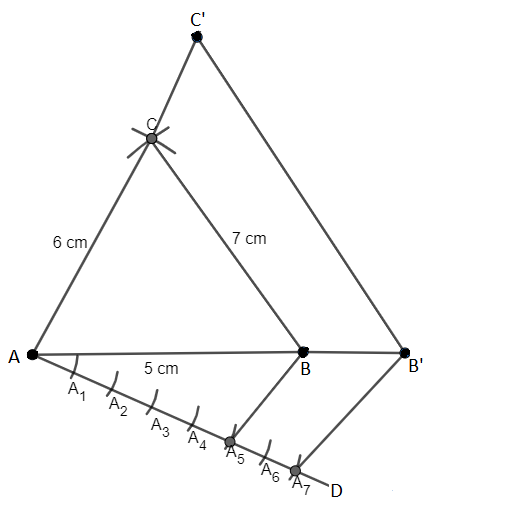
(i) Firstly draw a line segment AB of length 5 cm.

(ii) Now cut an arc of radius 6 cm from point A and an arc of 7 cm from point B.

(iii) Name the point of intersection of arcs to be point C.

(iv) Now join point AC and BC. Thus \Delta ABC is the required triangle.

(v) Draw a line AD which makes an acute angle with AB and is opposite of vertex C.

(vi) Cut seven equal parts of line AD namely AA 1 , AA 2 , AA 3 , AA 4 , AA 5 , AA 6 , AA 7 ,.

(vii) Now join A 5 to B. Draw a line A 7 B' parallel to A 5 B.

(viii) And then draw a line B'C' parallel to BC.

Hence \Delta AB'C' is the required triangle.

1636090397260

Q4 Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/ 2 times the corresponding sides of the isosceles triangle.

Answer:

Steps of construction:-

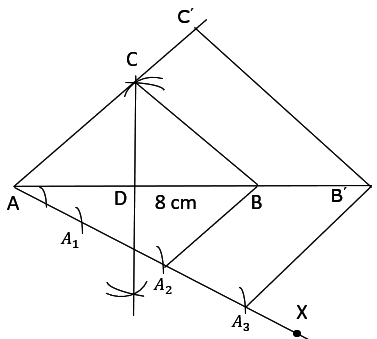
(i) Draw a line segment AB of length 8 cm.

(ii) Cut arcs taking point A and point B as the center. Draw the line to intersect on line segment AB. Mark the intersecting point as point D.

(iii) Cut arc of length 4 cm on the same line which will be the altitude of the triangle.

(iv) Name the point as C. Then \Delta ABC is the isosceles triangle.

(v) Draw a line AX which makes an acute angle with AB and is opposite of vertex C.

(vi) Cut seven equal parts of line AX namely AA 1 , AA 2 , AA 3 .

(vii) Now join A 2 to B. Draw a line A 3 B' parallel to A 2 B.

(viii) And then draw a line B'C' parallel to BC.

Hence \Delta AB'C' is the required triangle.

1636090408707

Q5 Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and \angle ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.

Answer:

Steps of construction:-

(i) Draw a line segment BC with a measurement of 6 cm.

(ii) Now construct angle 60 o from point B and draw AB = 5 cm.

(iii) Join point C with point A. Thus \Delta ABC is the required triangle.

(iv) Draw a line BX which makes an acute angle with BC and is opposite of vertex A.

(v) Cut four equal parts of line BX namely BB 1 , BB 2 , BB 3 , BB 4.

(vi) Now join B 4 to C. Draw a line B 3 C' parallel to B 4 C.

(vii) And then draw a line B'C' parallel to BC.

Hence \Delta AB'C' is the required triangle.

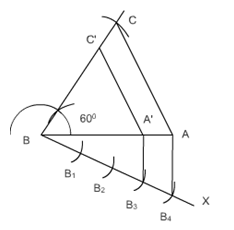
1636090424003

Q6 Draw a triangle ABC with side BC = 7 cm, \angle B = 45°, \angle A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of D ABC.

Answer:

Steps of construction:-

(i) Draw a line segment BC.

(ii) Now draw an angle \angle B = 45 o and \angle C = 30 o and draw rays in these directions.

(iii) Name the intersection of these lines as A.

(iv) Thus \bigtriangleup ABC is the required triangle.

(v) Draw a line BX which makes an acute angle with BC and is opposite of vertex A.

(vi) Cut four equal parts of line BX namely BB 1 , BB 2 , BB 3 , BB 4.

(vii) Now join B 3 to C. Draw a line B 4 C' parallel to B 3 C.

(viii) And then draw a line B'C' parallel to BC.

Hence \Delta AB'C' is the required triangle.

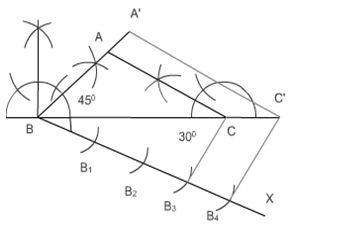
1636090438268

Q7 Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.

Answer:

Steps of construction:-

(i) Draw a line segment AB having a length of 4 cm.

(ii) Now, construct a right angle at point A and make a line of 3 cm.

(iii) Name this point C. Thus \Delta ABC is the required triangle.

(iv) Draw a line AX which makes an acute angle with AB and is opposite of vertex C.

(v) Cut four equal parts of line AX namely AA 1 , AA 2 , AA 3 , AA 4 , AA 5 .

(vi) Now join A 3 to B. Draw a line A 5 B' parallel to A 3 B.

(vii) And then draw a line B'C' parallel to BC.

Hence \Delta AB'C' is the required triangle.

1636090455562



More About NCERT Solutions for Class 10 Maths Chapter 11 Exercise 11.1

This section contains the extra information the source and scenario of content present in exercise 11.1 Class 10 Maths. Starting from the first. This exercise 11.1 Class 10 is there to represent the problems based on building triangles over conditions provided and given measurements i.e. AB and AC in triangle ABC. As the number increases in ascending for the questions, concepts get changed like here will be discussing other questions based on the property of the triangle mentioned in the previous chapter. So in simple words, we say Class 10 Maths chapter 11 exercise 11.1 is basically a Platform in the roadmap to learn more about 2D Geometry for beginners.

Also Read| Constructions Class 10 Notes

Benefits of NCERT Solutions for Class 10 Maths Chapter 11 Exercise 11.1

  • NCERT solutions for Class 10 Maths chapter 11 exercise 11.1 are important as to get better understanding over the subject.

  • Another benefit of exercise 11.1 Class 10 Maths is makes students understand terminologies like construction procedures and justification of the given diagram.

  • Student can solve most of the question provided to him/her in his HW, exams or test.

Also see-

NCERT Solutions Subject Wise

Frequently Asked Questions (FAQs)

1. What is the sum of all angles of the triangle?

The sum of all angles of triangle is 180 degrees 

2. A point A is 8 cm from the center of a circle with a radius of 10 cm. What is the maximum number of tangents that may be traced from point A to the circle?

The radius of the given circle is  10cm and point A is 8 cm from center of circle hence

The point lies inside of the circle hence no tangents can be traced from that point

3. A perpendicular line segment traced from the vertex of a triangle to the opposite side is called a

A perpendicular line segment traced from the vertex of a triangle to the opposite side is called an Altitude

4. How many Exercises are there in chapter 11 Class 10 Maths?

There are a total of 2 exercises in chapters 11 ie exercise 11.1 and 11.2

5. Is Exercise 11.1 Tough?

 Toughness of any chapter exercise and topic is based on the amount of hard work required to master that thing. As far as this chapter is concerned students need to follow definite path in order to solve each and every question of maths

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

View All School Exams

Certifications By Top Providers

Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:18 PM IST :
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST

Stay up-to date with CBSE Class 10th News

Back to top