NCERT Class 9 Maths Chapter 12 Notes Heron's Formula (Download PDF)

Class 9 Chapter 10 Heron's Formula Notes PDF – Download Free Study Material

Careers360 brings you NCERT Class 9 Maths Chapter 10 Heron's Formula notes, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.

Download PDF

NCERT Notes Class 9 Maths Chapter 10 Heron's Formula

Triangle: A geometrical closed figure that has three sides, three angles and three corners. The three corners are also called the vertices of the triangle.

Types of Triangles

Triangles can be divided into two categories:
1. Based on sides
2. Based on angels

Based on Sides

1. Equilateral Triangle
2. Isosceles Triangle
3. Scalene Triangle

Equilateral Triangle

A triangle in which all sides are equal is called an equilateral triangle.

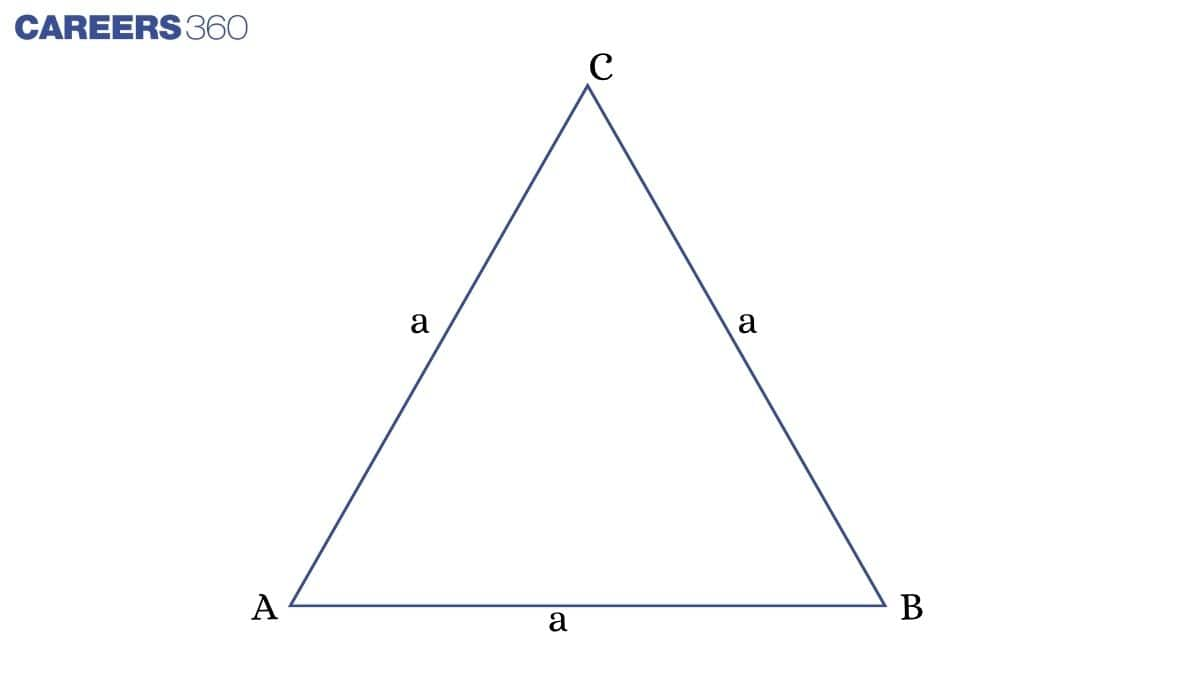
Area of equilateral triangle = $\frac{\sqrt3}{4}a^2$

Perimeter of equilateral triangle = $3a$

Where,

a is the side of the triangle.

Example: Find the area and perimeter of the equilateral triangle, in which the length of the side is 10cm.

Area of equilateral triangle = $\frac{\sqrt3}{4}10^2$

= $25\sqrt3$$cm^2$

Perimeter of equilateral triangle = $3 × 10$

= $30$

Isosceles Triangle

A triangle in which any two sides are equal is called an isosceles triangle.

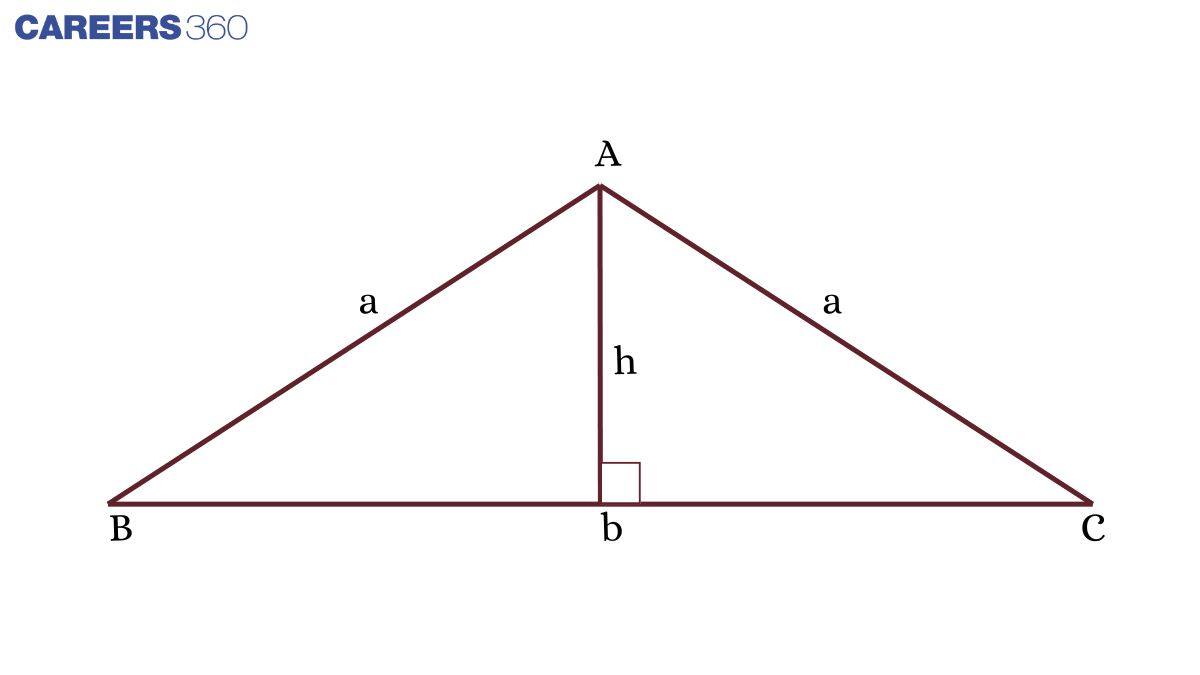
Area of isosclales triangle = $\frac{1}{2}bh$

Perimeter of an isosceles triangle = $2a + b$

Example: Find the area and perimeter of the triangle whose base is 12 cm long and each equal side is 16 cm long.

Area of isosclales triangle = $\frac{1}{2}12 × 16$

Area of isosclales triangle = $96$

Perimeter of an isosceles triangle = $2 × 16 + 12$

Perimeter of an isosceles triangle = $44$

Scalene Triangle

A triangle where the length of each side is different is known as a scalene triangle.

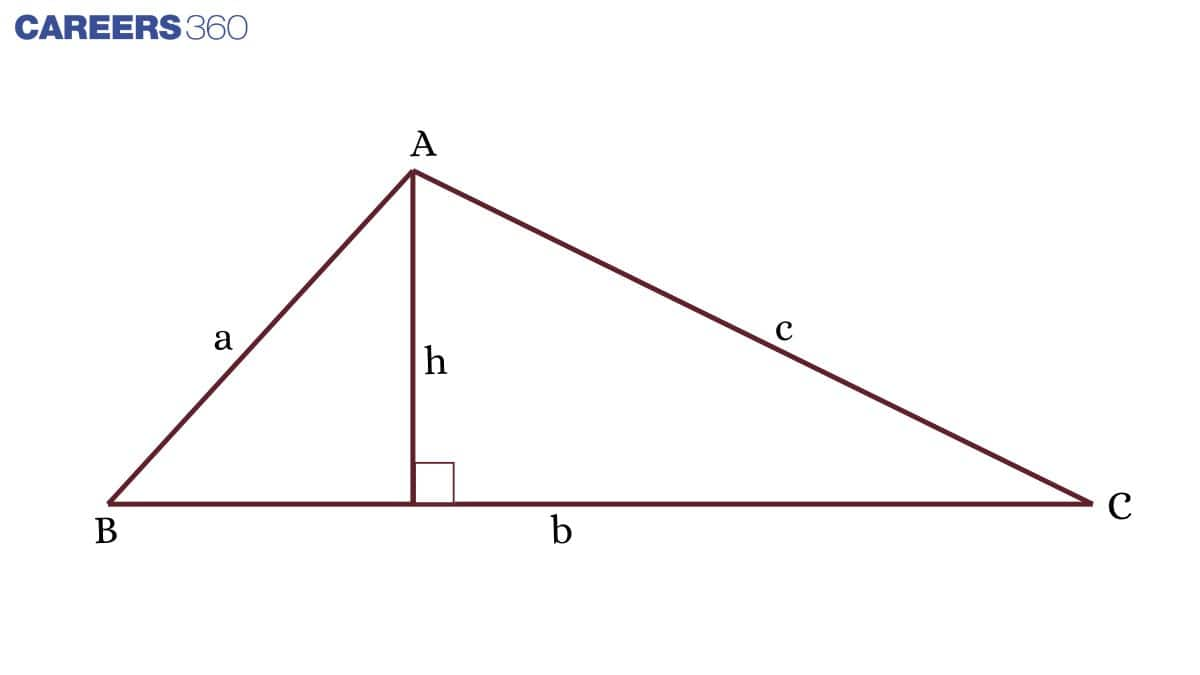
Area of scalene triangle = $\frac{1}{2}bh$

Perimeter of an scalene triangle = $a + b + c$

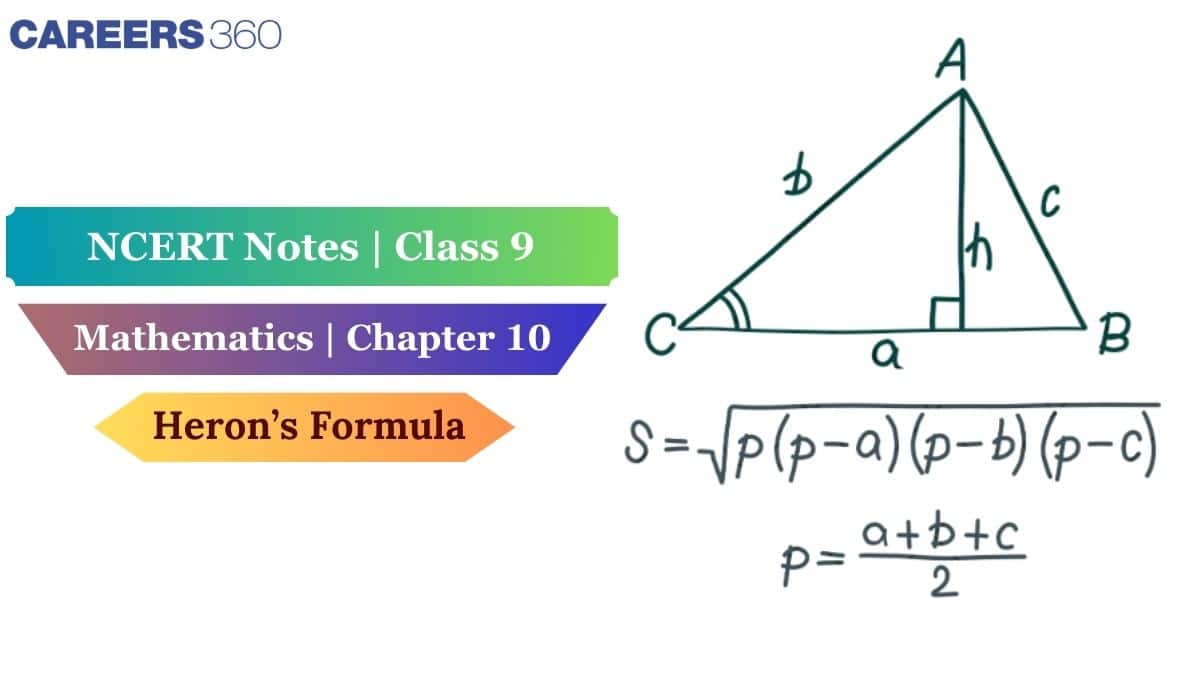
Area of a Triangle by Heron's Formula

Heron was a mathematician and an engineer in Alexandria in Egypt. He defined a formula to determine the area of a triangle when all three sides are known. The Heron's formula for determining the area of a triangle is as follows:

Semiperimeter (S) = $\frac{(a + b + c)}{2}$

Where a, b, and c are the sides of the triangle.

Area of triangle = $\sqrt {s(s - a)(s - b)(s - c)}$

Example: Find the area of a triangle whose sides are 4 cm, 5 cm and 7cm, respectively.

Semiperimeter (S) = $\frac{(a + b + c)}{2}$

Semiperimeter (S) = $\frac{(4 + 5 + 7)}{2}$

Semiperimeter (S) = $8$

Area of triangle = $\sqrt {8(8 - 4)(8 - 5)(8 - 7)}$

Area of triangle = $\sqrt {96}$$cm^2$

Heron's Formula: Previous Year Question and Answer

Question 1:
The three sides of a triangle are 7 cm, 9 cm, and 8 cm. What is the area of the triangle?

Solution:

Using the formula:
$s = \frac{(a + b + c)}{2}$
$s = \frac{(7 + 9 + 8)}{2}$
$s = \frac{24}{2}$
$s = 12$ cm
Now, plug the values of a, b, c, and s into Heron's formula to find the area of the triangle:
$\sqrt{(s(s - a)(s - b)(s - c))}$
$=\sqrt{(12(12 - 7)(12 - 9)(12 - 8))}$
$=\sqrt{(12 × 5 × 3 × 4)}$
$=12\sqrt{5}$ Sq. cm
Therefore, the area of the triangle with side lengths 7 cm, 9 cm, and 8 cm is approximately $12\sqrt{5}$ Sq. cm
Hence, the correct answer is $12 \sqrt{5} \;\mathrm{Sq}. \mathrm{cm}$.

Question 2:
The sides of a triangle are 8 cm, 12 cm, and 16 cm. What is the area of the triangle?

Solution:

The sides of the triangle are 8 cm, 12 cm, and 16 cm.
Semi perimeter = $\frac{8+12+16}{2}$ = 18
Area of the triangle = $\sqrt{18×(18 - 8)×(18 - 12)×(18 -16)}$
= $\sqrt{18×10×6×2}$
= $\sqrt{2160}$
= $12\sqrt{15}\ \text{cm}^2$
Hence, the correct answer is $12\sqrt{15}~\text{cm}^2$.

Question 3:
Find the area of a triangle whose sides are 10 cm, 12 cm, and 18 cm.

Solution:

The area of a triangle by Heron's formula = $\sqrt{s(s - a)(s - b)(s - c)}$
where $a$, $b$, and $c$ are the sides of the triangle, and $s$ is the semi-perimeter of the triangle.
Now, $s = \frac{a + b + c}{2}= \frac{10 + 12 + 18}{2} = 20$
So, the area $=\sqrt{20(20 - 10)(20 - 12)(20 - 18)} = \sqrt{20 \times 10 \times 8 \times 2} = 40 \sqrt{2} \text{ cm}^2$
Hence, the correct answer is $40 \sqrt{2} \text{ cm}^2$.

NCERT Class 9 Maths Notes – Chapter-Wise Links

Access all NCERT Class 9 Maths notes from one place using the links below.

NCERT Solutions for Class 9

Students must check the NCERT solutions for Class 9 Maths and Science given below:

• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Science

NCERT Exemplar Solutions for Class 9

Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:

• NCERT Exemplar Class 9 Maths Solutions
• NCERT Exemplar Class 9 Science Solutions

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books Class 9 Maths
• NCERT Syllabus Class 9 Maths
• NCERT Books Class 9
• NCERT Syllabus Class 9
• NCERT Books for Class 9 Science