• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Class 6 Maths Chapter 11 Algebra

NCERT Solutions for Class 6 Maths Chapter 11 Algebra

Edited By Ramraj Saini | Updated on Nov 30, 2023 10:11 AM IST

NCERT Solutions for Class 6 Maths Chapter 11 Algebra are discussed in this article. These NCERT solutions are created by expert team at careers360 considering the latest CBSE syllabus 2023. This is a very important branch of mathematics comprising 5 exercises and 27 questions. You will get NCERT Class 6 Maths solutions of chapter 11 for these all questions. In this NCERT solutions for Algebra class 6 Maths chapter 11, you will study algebraic expressions. This chapter of NCERT will give you some basics of algebra. These CBSE NCERT solutions for Class 6 Maths chapter 11 algebra are very useful in solving many real-life problems using variables.

This Story also Contains
  1. NCERT Solutions for Class 6 Maths Chapter 11 Algebra - Important Formulae
  2. NCERT Solutions for Class 6 Maths Chapter 11 Algebra - Important Points
  3. NCERT Solutions for Class 6 Maths Chapter 11 Algebra
  4. NCERT Solutions for Class 6 Maths Chapter 11 Algebra (Intext Questions and Exercise)
  5. NCERT Solutions for Class 6 Maths Chapter 11 Exercise 11.1
  6. NCERT Solutions for Class 6 Maths Chapter 11 E xercise 11.2
  7. NCERT Solutions for Class 6 Maths Chapter 11 E xercise 11.3
  8. NCERT Solutions for Class 6 Maths Chapter 11 Exercise 11.4
  9. NCERT Solutions for Class 6 Maths Chapter 11 Exercise 11.5
  10. Key Features of NCERT Solutions for Class 6 Maths Chapter 11 Algebra
  11. NCERT Solutions for Class 6 Mathematics Chapter Wise
  12. NCERT Solutions for Class 6 - Subject Wise
NCERT Solutions for Class 6 Maths Chapter 11 Algebra
NCERT Solutions for Class 6 Maths Chapter 11 Algebra

There are many questions in solutions of NCERT for Class 6 Maths chapter 11 algebra where you will learn to form an equation and solve them. Apart from that, there are some practice questions given at the end of every topic for conceptual clarity. NCERT Solutions for Class 6 are prepared by expert faculty to clear doubts which will aid you to understand the concepts given in NCERT 6 Class Maths Syllabus. Scroll down to access NCERT solutions for Class 6 Maths chapter 11. Also, Check NCERT Solutions to get class 6 to 12 solutions for Science and Maths. Understanding the concept of variables and equations are mandatory for our higher studies. So solving all the NCERT questions are mandatory. Solve as many questions as possible from this chapter.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra - Important Formulae

  1. literal numbers or literals = Letters to represent numbers

  2. Commutative property of addition, a + b = b + a, where variables a and b can represent any number.

  3. Consider two literal numbers x and y

  • x∗y = xy

  • 5∗x = 5x

  • x∗3 = 3x

  1. a∗a∗.............∗a (12 times ) = a12

  2. In expressions like this x9, the number 9 is called the index or exponent, and the letter x is called the base.

  3. Constant = Same numerical value

NCERT Solutions for Class 6 Maths Chapter 11 Algebra - Important Points

Patterns using matchsticks: Exploring the arrangement of matchsticks to create letters and shapes, identifying the number of matchsticks required for repeating a given shape.

Variable: A symbol or letter (e.g., n) that represents a quantity or value that can vary or change. The value of a variable is not fixed and can take on different values.

Fixed value: Some quantities, like the number of angles in a triangle, have a specific and unchanging value. They are not variables.

Expressing relations: Variables allow us to express relationships and connections between quantities in various practical situations.

Operations on variables: Variables can be manipulated using operations such as addition, subtraction, multiplication, and division, similar to fixed numbers. Expressions involving variables can be formed, such as x - 3, x + 3, 2n, 5m, 3p, 2y + 3, 3l - 5, etc.

General rules: Variables enable us to express general rules and principles in both geometry and arithmetic. For example, the

Equation: A mathematical statement that equates two expressions or quantities. It states that the expression on the left-hand side (LHS) is equal to the expression on the right-hand side (RHS), using the equal (=) sign. For example, x - 3 = 10 is an equation.

LHS and RHS: An equation has two sides, the left-hand side (LHS) and the right-hand side (RHS), with the equal (=) sign in between.

Solution of an equation: The specific value(s) of the variable that satisfy the equation, making both the LHS and RHS of the equation equal. These values are called the solutions of the equation.

Trial and error method: A method for finding the solution(s) of an equation by systematically trying different values for the variable and checking if they satisfy the equation. Different values are tested until the correct value that satisfies the equation is found.

Free Download NCERT Solutions for Class 6 Maths Chapter 11 Algebra For CBSE Exam

NCERT Solutions for Class 6 Maths Chapter 11 Algebra

Download PDF

NCERT Solutions for Class 6 Maths Chapter 11 Algebra (Intext Questions and Exercise)

NCERT Solutions for Class 6 Maths Chapter 11 Exercise 11.1

Question: 1 Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.

(a) A pattern of letter T as aa1_SOFwWIh .

(b) A pattern of letter Z as aa2 .

(c) A pattern of letter U as aa3 .

(d) A pattern of letter V as aa4 .

(e) A pattern of letter E as aa5 .

(f) A pattern of letter S as aa6 .

(g) A pattern of letter A as aa7 .

Answer:

(a) A pattern of letter T as aa1_5U6igJs =2n ( because 2 matchsticks are used )

(b) A pattern of letter Z as aa2_jFEE3vz =3n ( because 3 matchsticks are used )

(c) A pattern of letter U as aa3_gZToPAu =3n ( because 3 matchsticks are used )

(d) A pattern of letter V as aa4_qXKYuht =2n ( because 2 matchsticks are used )

(e) A pattern of letter E as aa4_DHmWqZl =5n ( because 5 matchsticks are used )

(f) A pattern of letter S as aa6_dhsN9JN =5n ( because 5 matchsticks are used )

(g) A pattern of letter A as aa7_PfRCZcN =6n ( because 6 matchsticks are used )

Question: 2 We already know the rule for the pattern of letters L,C and F . Some of the letters from Q.1 (given above) give us the same rule as that given by L. Which are these? Why does this happen?

Answer: Letter "T" and "v" has pattern 2n because 2 matchsticks are used in these two letters.

Question: 3 Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use n for the number of rows.)

Answer: Cadets in a row = 5

number of rows = n

Thus, the total number of cadets = 5n

Question: 4 If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b for the number of boxes.)

Answer: Mangoes in a box = 50

Number of boxes = b

Thus, the total number of mangoes = 50b

Question: 5 The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use s for the number of students.)

Answer: pencils per student = 5

number of students = s

Thus, the total pencils needed = 5s

Question: 6 A bird flies 1 kilometer in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (Use t for flying time in minutes.)

Answer: Time taken by bird = t minutes

Speed of bird = 1 km per minute

Thus, distance covered by bird =speed\times time

=1\times t=t \,\, \, \, km

Question: 7 Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots) with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?

Answer: Number of rows = r

Number of dots in each row = 9 dots

Thus, the total number of dots = 9r

When the number of rows is 8, then the total number of dots are 9\times8 =72 dots.

When the number of rows is 10, then the total number of dots are 9\times 10=90 dots.

Question: 8 Leela is Radha's younger sister. Leela is 4 years younger than Radha. Can you write Leela's age in terms of Radha's age? Take Radha's age to be x years

Answer: Radha's age = x years

Thus, age of Leela = (x-4) years

Question: 9 Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is l, how many laddus did she make?

Answer: Number of laddus given = l

Number of laddus remaining = 5

Thus,tota number of laddus = (l+5)

Question: 10 Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x. what is the number of oranges in the larger box?

Answer: Number of oranges in one box = x

Number of box = 2

So, the total number of oranges = 2x

Remaining number of oranges = 10

Thus, the number of oranges = 2x+10

Question: 11 (a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks

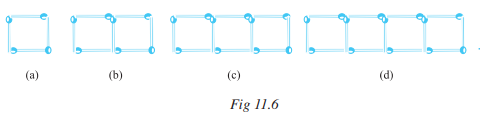
1643095732551

in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)

Answer:

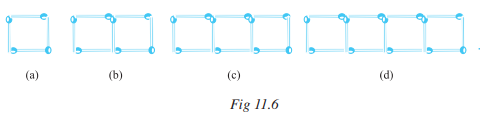
1643095802819

(a) 4 matchsticks

(b) 7 matchsticks

(c) 10 matchsticks

(d) 13 matchsticks

If we remove 1 matchstick from each then it forms a table of 3 i.e.,3,6,9,12,.....

So, required equation = 3x+1 , x= number of squares

Question: 11 (b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.

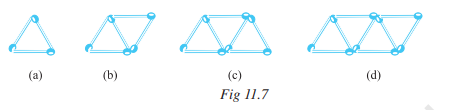
1643095869541

Answer:

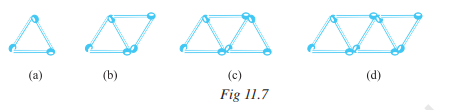
1643095901644

(a) 3 matchsticks

(b) 5 matchsticks

(c) 7 matchsticks

(d) 9 matchsticks

If we remove 1 matchstick from each then it forms a table of 2 i.e., 2,4,6,8............

So, required equation = 2x+1 , x= number of triangles

NCERT Solutions for Class 6 Maths Chapter 11 E xercise 11.2

Question: 1 The side of an equilateral triangle is shown by l . Express the perimeter of the equilateral triangle using

l.

Answer: The side of an equilateral triangle is l .

Therefore, the perimeter of the equilateral triangle =3 \times side=3l

Question: 2 The side of a regular hexagon (Fig 11.10) is denoted by l. Express the perimeter of the hexagon using l. (Hint: A regular hexagon has all its six sides equal in length.)

1643095953342

Answer: The side of a hexagon is l.

Therefore, the perimeter of the hexagon =6 \times side=6l

Question: 3 A cube is a three-dimensional figure as shown in Fig 11.11. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.

1643096005864

Answer: Length of one edge of cube = l

Number of edges in a cube = 12

So, total length = 12 \times l=12l

Question:4 The diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius

(r).

1643096072960

Answer: Length of diameter is double the length of the radius.
Thus,d = 2r

Question: 5 To find sum of three numbers 14, 27 and 13, we can have two ways:

(a) We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or

(b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus, (14+27)+13=14+(27+13)

This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on Whole Numbers, in a general way, by using variables a, b and c.

Answer: According to the given condition,

(a+b)+c=a+(b+c)

NCERT Solutions for Class 6 Maths Chapter 11 E xercise 11.3

Question: 1 Make up as many expressions with numbers (no variables) as you can from three numbers 5,7 and 8. Every number should be used not more than once. Use only addition, subtraction and multiplication.(Hint: Three possible expressions are 5+(8-7),\ 5-(8-7), \ (5\times8)+7 make the other expressions.)

Answer: The other expressions are :

(i) (8\times 5)-7

(ii)(8+5)-7

(iii)(8+7)-5

(iv)(8\times 7)-5

(v) 5\times (7+8)

(vi) 5\times (7\times 8)

(vii) 5-(7+ 8)

(viii) 5+(8-7)

Question: 2 Which out of the following are expressions with numbers only?

(a) y+3

(b) (7\times 20)-8z

(c) 5(21-7)+7\times 2

(d) 5

(e) 3x

(f) 5-5n

(g) (7\times 20)-(5\times 10)-45+p

Answer: Option (c) and (d) are with numbers only. All other expression contains alphabets

Question: 3 Identify the operations (addition, subtraction, division, multiplication) in forming the following expressions and tell how the expressions have been formed.

(a) z+1,z-1,y+17,y-17

(b) 17y,\frac{y}{17},5z

(c) 2y+17,2y-17

(d) 7m,-7m+3,-7m-3

Answer:

(a) z+1\rightarrow addition y-17\rightarrow subtraction

z-1\rightarrow subtraction y+17\rightarrow addition

(b) 17y\rightarrow multiplication \frac{y}{17}\rightarrow division

5z\rightarrow multiplication

(c) 2y+17\rightarrow multiplication \, \, and\, \, \, addition

2y-17\rightarrow multiplication \, \, and\, \, \, subtraction

(d) 7m\rightarrow multiplication

-7m+3\rightarrow multiplication\, \, and\, \, addition

-7m-3\rightarrow multiplication\, \, and\, \, subtraction

Question: 4(i) Give expressions for the following cases.

(a) 7 added to p

(b) 7 subtracted from p

(c) p multiplied by 7

(d) p divided by 7

(e) 7 subtracted from -m

(f) -p multiplied by 5

(g) -p divided by 5

(h) p multiplied by -5

Answer:

(a) 7 added to p =p+7

(b) 7 subtracted from p =p-7

(c) p multiplied by 7 =p\times 7=7p

(d) p divided by 7 =\frac{p}{7}

(e) 7 subtracted from -m =-m-7

(f) -p multiplied by 5 =-5p

(g) -p divided by 5 =\frac{-p}{5}

(h) p multiplied by -5 =-5p

Question: 4(ii) Give expressions for the following cases.

(e) 7 subtracted from -m

(f) -p multiplied by 5

(g) -p divided by 5

(h) p multiplied by -5

Answer:

(e) 7 subtracted from -m = -m-7

(f) -p multiplied by 5

(g) -p divided by 5

(h) p multiplied by -5

Question:5(i) Give expressions in the following cases.

(a) 11 added to 2m

(b) 11 subtracted from 2m

c) 5 times y to which 3 is added

(d) 5 times y from which 3 is subtracted

(e) y is multiplied by -8

Answer:

(a) 11 added to 2m =2m+11

(b) 11 subtracted from 2m =2m-11

c) 5 times y to which 3 is added =5y+3

(d) 5 times y from which 3 is subtracted =5y-3

(e) y is multiplied by -8 =-8y

Question: 5(ii) Give expressions in the following cases.

(f) y is multiplied by -8 and then 5 is added to the result

(g) y is multiplied by 5 and the result is subtracted from 16

(h) y is multiplied by -5 and the result is added to 16.

Answer:

(f) y is multiplied by -8 and then 5 is added to the result= -8y+5

(g) y is multiplied by 5 and the result is subtracted from 16 =16-5y

(h) y is multiplied by -5 and the result is added to 16. =-5y+16

Question: 6 (a) Form expressions using t and 4. Use not more than one number operation. Every expression must have t in it.

Answer: According to given condition,

t+4,t-4,4-t,4t,\frac{t}{4},\frac{4}{t}

Question: 6 (b) Form expressions using y, 2 and 7 . Every expression must have y in it. Use only two number operations. These should be different.

Answer: According to the given condition,

2y+7,2y-7,7y+2,7y-2

NCERT Solutions for Class 6 Maths Chapter 11 Exercise 11.4

Question:1 Answer the following:

(a) Take Sarita’s present age to be y years

(i) What will be her age 5 years from now?

(ii) What was her age 3 years back?

(iii) Sarita’s grandfather is 6 times her age. What is the age of her grandfather?

(iv) Grandmother is 2 years younger than grandfather. What is grandmother's age?

(v) Sarita’s father’s age is 5 years more than 3 times Sarita’s age. What is her father's age?

Answer: According to the given condition,

(a) (i) y+5

(ii) y-3

(iii) 6y

(iv) 6y-2

(v) 3y+5

Question: 1 (b) The length of a rectangular hall is 4 meters less than 3 times the breadth of the hall. What is the length, if the breadth is b meters?

Answer: Breadth = b

And length = (3b-4) meters

Question: 1 (c) A rectangular box has height h\; cm. Its length is 5 times the height and breadth is 10\; cm less than the length. Express the length and the breadth of the box in terms of the height.

Answer: Height of box = h cm

Length of box = 5 times height = 5h cm

Breadth of box = 10 cm less than length = (5h-10) cm

Question: 1 (d) Meena, Beena and Leena are climbing the steps to the hill top. Meena is at step s, Beena is 8 steps ahead and Leena 7 steps behind. Where are Beena and Meena? The total number of steps to the hilltop is 10 less than 4 times what Meena has reached. Express the total number of steps using s.

Answer: Meena's position = s

Beena's position = 8 steps ahead = s+8

Leena's position =7 steps behind = s-7

Total steps = 4s-10

Question: 1 (e) A bus travels at per hour. It is going from Daspur to Beespur. After the bus has travelled hours, Beespur is still away. What is the distance from Daspur to Beespur? Express it using v?

Answer: Speed of bus = v km\h

Distance travelled in 5 hours = 5v km

Remaining distance = 20 km

Totsl distance = (5v+20)km

Question: 2 Change the following statements using expressions into statements in ordinary language. (For example, Given Salim scores r runs in a cricket match, Nalin scores (r + 15) runs. In ordinary language – Nalin scores 15 runs more than Salim.)

(a) A notebook costs ` Rs.p .A book costs Rs.3p.

(b) Tony puts q marbles on the table. He has 8\; q marbles in his box.

(c) Our class has n students. The school has 20\; n students.

(d) Jaggu is z years old. His uncle is 4\; z years old and his aunt is (4\; z-3) years old.

(e) In an arrangement of dots there are r rows. Each row contains 5 dots.

Answer:

(a) A book cost 3 times the cost of a notebook.

(b) The number of marbles in the box is 8 times marbles on the table.

(c) The total number of students in school is 20 times that in our class.

(d) Jaggu's uncle's age is 4 times the age of Jaggu. Jaggu's aunt is 3 years younger than his uncle.

(e) The total number of dots is 5 times the number of rows.

Question: 3 (a) Given Munnu’s age to be x years, can you guess what (x-2) may show? (Hint : Think of Munnu’s younger brother.)

Can you guess what (x+4) may show? What (3x+7) may show?

Answer:

(a) Munnu's age = x years

Munnu’s younger brother is 2years younger than him = (x-2) years

Munnu’s elder brother is 4years older than him = (x+4) years

His father is 7 years more than thrice of his age = (3x+7)years

Question: 3 (b) Given Sara’s age today to be y years. Think of her age in the future or in the past. What will the following expression indicate?

y+7, y-3, y+4\frac{1}{2}, y-2\frac{1}{2}.

Answer:

Her age in past = (y-3),(y-2\frac{1}{2})

Her age in future = (y+7),(y+4\frac{1}{2})

Question: 3 (c) Given n students in the class like football, what may 2n show? What may \frac{n}{2} show? (Hint : Think of games other than football).

Answer:

Number of students like hockey is twice the students like football, i.e.,2n

Number of students like tennis is half the students like football, i.e., \frac{n}{2}

NCERT Solutions for Class 6 Maths Chapter 11 Exercise 11.5

Question: 1(a) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

17=x+7

Answer: (a) It is an equation of variable as both sides are equal. The variable is x.

Question: 1(b ) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

(t-7)> 5

Answer: (b) It is not an equation as LHS is greater than RHS.

Question: 1(c) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

\frac{4}{2}=2

Answer: (c) It is an equation with no variable. We may call this a numerical equation

Question: 1(d) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

(7\times 3)-19=8

Answer: (d) It is an equation with no variable. It is a numerical equation.

Question: 1(e) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable. 5\times 4-8=2\; x

Answer: (e) It is an equation of variable as both sides are equal. The variable is x.

Question: 1(f) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

x-2=0 .

Answer: (f) It is an equation of variable x.

Question: 1 (g) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

2m< 30

Answer: (g) It is not an equation because LHS is less than RHS.

Question: 1(h) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

2n+1=11

Answer: (h) It is an equation of variable as both sides are equal. The variable is n.

Question: 1(i) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable

7=(11\times 5)-(12\times 4)

Answer: (i) It is an equation with no variable as both sides are equal.

Question: 1(j) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

7=(11\times 2)+p

Answer: (j) It is equation of variable p.

Question: 1(k) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

20=5y

Answer: (k) It is an equation of varaible y.

Question: 1(l) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

\frac{3q}{2}< 5

Answer: (l) It is not an equation as LHS is less than RHS.

Question: 1(m) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

z+12> 24

Answer: (m) It is not an equation as LHS is greater than RHS.

Question: 1(n) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

20-(10-5)=3\times 5

Answer: (n) It is an equation with no variable.

Question:1(o) State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.

7-x=5

Answer: (o) It is an equation of variable x.

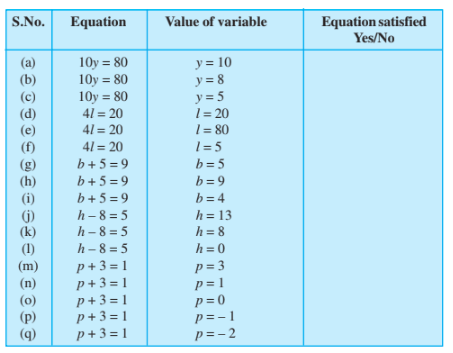
Question: 2 Complete the entries in the third column of the table.

1643096149145

Answer:

S. no.

Equation

Value of variable

Equ.satisfied Yes/No

Sol. of LHS

(a)

10 y =80

y = 10

No

10\times 10=100

(b)

10 y = 80

y = 8

Yes

10\times 8=80

(c)

10 y = 80

y = 5

No

10\times 5=50

(d)

4l = 20

l = 20

No

4\times 20=80

(e)

4l = 20

l = 80

No

4\times 80=320

(f)

4l = 20

l =5

Yes

4\times 5=20

(g)

b + 5 =9

b = 5

No

5+5=10

(h)

b + 5=9

b = 9

Yes

9+5=14

(i)

b+5=9

b = 4

Yes

13-8=5

(j)

h -8 =5

h =13

Yes

8-8=0

(k)

h -8 =5

h = 8

No

0-8=-8

(l)

h -8 =5

h = 0

No

3+3=6

(m)

p+3=1

p = 3

No

1+3= 4

(n)

p+3=1

p = 1

No

0+3= 3

(o)

p+3=1

p = 0

No

-1+3= 2

(p)

p+3=1

p = -1

Yes

-2+3= 1

(q)

p+3=1

p = -2



Question: 3 Pick out the solution from the values given in the bracket next to each equation. Show that the other values do not satisfy the equation.

(a) 5m=60 (10,5,12,15)

(b) n+12=20 (12,8,20,0)

(c) p-5=5 (0,10,5,-5)

(d) \frac{q}{2}=7 (7,2,10,14)

(e) r-4=0 (4,-4,8,0)

(f) x+4=2 (-2,0,2,4)

Answer:

(a) 5m=60

Putting given values in LHS.

5\times 10=50 5\times 12=60

\therefore LHS\neq RHS \therefore LHS= RHS

m = 10 is not a solution. m = 12 is a solution.

5\times 5=50 5\times 15=75

\therefore LHS\neq RHS \therefore LHS\neq RHS

m = 5 is not a solution. m = 15 is not a solution.

(b) n+12=20

Putting given values in LHS.

12+12=24 20+12=32

\therefore LHS\neq RHS \therefore LHS\neq RHS

n = 12 is not a solution. n = 20 is not a solution.

8+12=20 0+12=12

\therefore LHS= RHS \therefore LHS\neq RHS

n = 8 is a solution. n =0 is not a solution.

(c) p-5=5

Putting given values in LHS.

0-5=-5 10-5=5

\therefore LHS\neq RHS \therefore LHS= RHS

p =0 is not a solution. p = 10 is a solution.

5-5=0 -5-5=-10

\therefore LHS\neq RHS \therefore LHS\neq RHS

p = 5 is not a solution. p = -5 is not a solution

(d) \frac{q}{2}=7

Putting given values in LHS.

\frac{7}{2} \frac{2}{2}=1

\therefore LHS\neq RHS \therefore LHS\neq RHS

q =7 is not a solution. q = 2 is not a solution.

\frac{10}{2}=5 \frac{14}{2}=7

\therefore LHS\neq RHS \therefore LHS= RHS

q = 10 is not a solution. q = 14 is a solution.

(e) r-4=0

Putting given values in LHS.

4-4=0 -4-4=-8

\therefore LHS= RHS \therefore LHS\neq RHS

r =4 is a solution. r = -4 is not a solution.

8-4=4 0-4=-4

\therefore LHS\neq RHS \therefore LHS\neq RHS

r = 8 is not a solution. r = 0 is not a solution

(f) x+4=2

Putting given values in LHS.

-2+4=2 0+4=4

\therefore LHS= RHS \therefore LHS\neq RHS

x = -2 is a solution. x = 0 is a solution.

2+4=6 4+4=8

\therefore LHS\neq RHS \therefore LHS\neq RHS

x = 2 is not a solution. x = 4 is not a solution

Question: 4 (a) Complete the table and by inspection of the table find the solution to the equation

m+10=16.

1643096194400

Answer: (a)

m

1

2

3

4

5

6

7

8

9

10

11

12

13

m+10

11

12

13

14

15

16

17

18

19

20

21

22

23

At m = 6, m+10=16

Thus, m =6 is a solution.

Question: 4 (b) Complete the table and by inspection of the table, find the solution to the equation

5t=35.

1643096251145

Answer: (b)

t

3

4

5

6

7

8

9

10

11

12

13

14

15

16

5t

15

20

25

30

35

40

45

50

55

60

65

70

75

80

At t=7, 5t = 35

Thus, t = 7 is the solution.

Question: 4 (c) Complete the table and find the solution of the equation z/3=4 using the table.

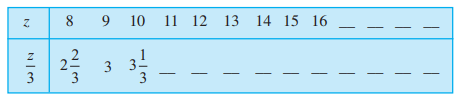
1643096323002

Answer: (c)

z

8

9

10

11

12

13

14

15

16

17

18

19

20

\frac{z}{3}

\frac{8}{3}

3

\frac{10}{3}

\frac{11}{3}

4

\frac{13}{3}

\frac{14}{3}

5

\frac{16}{3}

\frac{17}{3}

6

\frac{19}{3}

\frac{20}{3}

At z = 12 , \frac{z}{3}=4

Thus, z= 12 is a solution.

Question: 4 (d) Complete the table and find the solution to the equation

m-7=3.

1643096365427

Answer: (d)

m

5

6

7

8

9

10

11

12

13

14

15

m - 7

-2

-1

0

1

2

3

4

5

6

7

8

At m=10, m-7 = 3
Thus, m=10 is the solution

Question:5 Solve the following riddles, you may yourself construct such riddles.

(i) Go round a square Counting every corner Thrice and no more! Add the count to me To get exactly thirty four!

(ii) For each day of the week Make an upcount from me If you make no mistake You will get twenty three!

(iii) I am a special number Take away from me a six! A whole cricket team You will still be able to fix!

(iv) Tell me who I am I shall give a pretty clue! You will get me back If you take me out of twenty two!

Answer:

(i) Square has 4 sides.

Counting every corner Thrice and no more!

Implies we go around square thrice,i.e. 12 times.

Add the count to me To get exactly thirty - four!

Let us assume the number as y, we get 34.

12+y=34

y=34-12=22

So, 22 is the number .

(ii) If 23 is number for Sunday.

Then counting up, Saturday is 22, Friday is 21, Thursday is 20.

Wednesday is 19, Tuesday is 18, Monday is 17 and Sunday is 16.

Therefore, the number considered is 16.

(iii) Let the number be x.

If we take away 6 from x, we get a cricket team.

x - 6 = 11

x=11+6=17

Special number is 17.

(iv) Let the number be x.

22 - x = x

22 = 2x

x=\frac{22}{2}=11

The number is 11.

Key Features of NCERT Solutions for Class 6 Maths Chapter 11 Algebra

Additional Tips and Tricks: The class 6 maths algebra often provide additional tips and tricks to simplify calculations and improve efficiency. These insights can help students save time and enhance their problem-solving abilities.

Comprehensive Coverage: The class 6 chapter 11 maths solutions cover all the major topics in the chapter, including variables, constants, algebraic expressions, like terms, coefficients, equations, and solving equations using the trial and error method. Students can be confident that they are learning all the essential concepts required for a strong foundation in algebra.

Conceptual Clarity: The chapter 11 maths class 6 explain the fundamental concepts of algebra in a clear and concise manner. They break down complex topics into simpler steps, making it easier for students to understand.

Step-by-Step Approach: Each exercise in the chapter is solved step-by-step, ensuring that students can follow along and grasp the solution methodology. The solutions include detailed explanations for each step, making it easier for students to learn and apply the concepts.

Also Check

NCERT Books and NCERT Syllabus

NCERT Solutions for Class 6 Mathematics Chapter Wise

Chapters No. Chapters Name
Chapter - 1 Knowing Our Numbers
Chapter - 2 Whole Numbers
Chapter - 3 Playing with Numbers
Chapter - 4 Basic Geometrical Ideas
Chapter - 5 Understanding Elementary Shapes
Chapter - 6 Integers
Chapter - 7 Fractions
Chapter - 8 Decimals
Chapter - 9 Data Handling
Chapter -10 Mensuration
Chapter -11 Algebra
Chapter -12 Ratio and Proportion
Chapter -13 Symmetry
Chapter -14 Practical Geometry

NCERT Solutions for Class 6 - Subject Wise

NCERT Solutions for Class 6 Maths
NCERT Solutions for Class 6 Science

Benefits of NCERT Solutions for Class 6 Maths Chapter 11 Algebra

  • You will learn NCERT Class 6 Maths solutions chapter 11 very easily.
  • You can develop an algebraic expression of some real-life problems and solve them which you have learnt in this chapter.
  • It is going to help you with your homework as you can get detailed explanations of practice questions given at the end of every topic in the CBSE NCERT solutions for class 6 maths chapter 11 algebra.
  • You will get some short tricks and tips to solve some specific problems.
  • Tip- Mathematics required more practice to get conceptual clarity. So, you should solve all the NCERT questions including examples and practice questions on your own.

Happy learning!!!

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
MP: Private schools to pay back illegally collected tuition fees worth Rs 31 crores
Tamil Nadu teacher fatally stabbed in school, violence erupts; assailant detained
Bihar govt puts hold on new teachers transfer policy
Youth stabs teacher on school premises; now detained, says police
Air Pollution: Schools in Rajasthan's Khairthal-Tijara go online for classes 1 to 5
Govt informs SC about NCERT guidelines for development of e-content for children with disabilities
Government school principal in Andhra chops off girl students' hair for coming late
Back to top