NCERT Solutions for Class 6 Maths Chapter 5 Prime Time - Free PDF Download
Numbers are the music of the universe, silently keeping everything in flow. Numbers are all around us. We experience the presence of numbers in our daily lives in various forms. We are familiar with various types of numbers, such as whole numbers, natural numbers, fractions, etc. In this article, we will explore a specific category of numbers known as prime numbers. Every prime number is a VIP in the world of mathematics. We will learn about factor tree, co-prime numbers, composite numbers and much more. These NCERT Solutions for Class 6 Maths contain the step-by-step, comprehensive solutions for all the questions in this chapter on prime numbers. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 5 Prime Time: Download Free PDF
- Class 6 Maths Chapter 5 Prime Time: Exercise
- NCERT Prime Time Class 6 Maths Chapter 5 - Topics
- Class 6 Maths Chapter 5 Prime Time solutions: Extra Question
- NCERT Solutions for Class 6 Maths Chapter 5 Prime Time: Notes
- Class 6 Maths Chapter 5 Prime Time Solutions: Points to Remember
- Why are Class 6 Maths Chapter 5 Prime Time question answers important?
- NCERT Class 6 Maths Chapter Wise Solutions
- NCERT Books and the NCERT Syllabus

A prime number is a lonely hero in the number world, divisible only by 1 and itself. These NCERT Solutions for class 6 are one of the important study resources for students as they provide trustworthy and reliable step-by-step, comprehensive solutions for all the questions asked in each chapter of the NCERT textbook. Students can refer to these solutions during exam preparation to practice more problems and check their answers to find their weaknesses and work on those further. If you need notes, syllabus breakdown, or practice materials, this NCERT article has it all.
NCERT Solutions for Class 6 Maths Chapter 5 Prime Time: Download Free PDF
Careers360 brings you Class 6 Maths Chapter 5 Prime Time solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
Class 6 Maths Chapter 5 Prime Time: Exercise
Below are the detailed Class 6 Maths Chapter 5 Prime Time question answers provided in the textbook.
| Prime Time Class 6 Question Answers Page number: 108 Number of Questions: 4 |
Children sit in a circle and play a game of numbers. One of the children starts by saying ‘1’. The second player says ‘2’, and so on. But when it is the turn of 3, 6, 9, … (multiples of 3), the player should say ‘idli’ instead of the number. When it is the turn of 5, 10, … (multiples of 5), the player should say ‘vada’ instead of the number. When a number is both a multiple of 3 and a multiple of 5, the player should say ‘idli-vada’! If a player makes any mistake, they are out. The game continues in rounds till only one person remains. For which numbers should the players say ‘idli’ instead of saying the number? These would be 3, 6, 9, 12, 18, … and so on. For which numbers should the players say ‘vada’? These would be 5, 10, 15, 20, … and so on. Which is the first number for which the players should say, ‘idli-vada’? It is 15, which is a multiple of 3 and also a multiple of 5. Find out other such numbers that are multiples of both 3 and 5. These numbers are called _______Least Common Multiple (LCM)_____________________.
Question 1: At what number is ‘idli-vada’ said for the 10th time?
Solution: LCM of 3 and 5 is 15. (3 × 5 = 15)
So, “idli-vada” will be said 10th time at the number = 15 × 10 = 150
Hence, the correct answer is 150.
Question 2: If the game is played for the numbers 1 to 90, find out:
a. How many times would the children say ‘idli’ (including the times they say ‘idli-vada’)?
b. How many times would the children say ‘vada’ (including the times they say ‘idli-vada’)?
c. How many times would the children say ‘idli-vada’?
Solution:
a. Multiples of 3 are said to be “idli”.
Within 90 , the number of multiples of $3=\frac{90}{3}=30$
"Idli-vada" will be said when the number is both a multiple of 3 and 5.
LCM of 3 and 5 is $15. (3 \times 5=15)$
Within 90 , the number of multiples of $15=\frac{90}{15}=6$
$\therefore$ The number of times students will say "Idli" $=30+6=36$
Hence, the correct answer is 36.
b. Multiples of 5 are said to be "Vada".
Within 90 , the number of multiples of $5=\frac{90}{5}=18$
"Idli-vada" will be said when the number is both a multiple of 3 and 5.
LCM of 3 and 5 is $15. (3 \times 5=15)$
Within 90 , the number of multiples of $15=\frac{90}{15}=6$
$\therefore$ The number of times students will say "Idli" $=18+6=24$
Hence, the correct answer is 24.
c. "Idli-vada" will be said when the number is both a multiple of 3 and 5.
LCM of 3 and 5 is $15. (3 \times 5=15)$
Within 90 , the number of multiples of $15=\frac{90}{15}=6$
That will be the number of times children will say “Idli-vada”.
Hence, the correct answer is 6.
Question 3: What if the game was played till 900? How would your answers change?
Solution:
a. Multiples of 3 are said to be “idli”.
Within 900 , the number of multiples of $3=\frac{900}{3}=300$
"Idli-vada" will be said when the number is both a multiple of 3 and 5.
LCM of 3 and 5 is $15. (3 \times 5=15)$
Within 90 , the number of multiples of $15=\frac{900}{15}=60$
$\therefore$ The number of times students will say "Idli" $=300+60=360$
So, the value will be 10 times greater than the previous answer.
b. Multiples of 5 are said to be "Vada".
Within 90 , the number of multiples of $5=\frac{900}{5}=180$
"Idli-vada" will be said when the number is both a multiple of 3 and 5.
LCM of 3 and 5 is $15. (3 \times 5=15)$
Within 90 , the number of multiples of $15=\frac{900}{15}=60$
$\therefore$ The number of times students will say "Idli" $=180+60=240$
So, the value will be 10 times greater than the previous answer.
c. "Idli-vada" will be said when the number is both a multiple of 3 and 5.
LCM of 3 and 5 is $15. (3 \times 5=15)$
Within 90 , the number of multiples of $15=\frac{900}{15}=60$
That will be the number of times children will say "Idli-vada".
So, the value will be 10 times greater than the previous answer.
Question 4: Is this figure somehow related to the ‘idli-vada’ game?
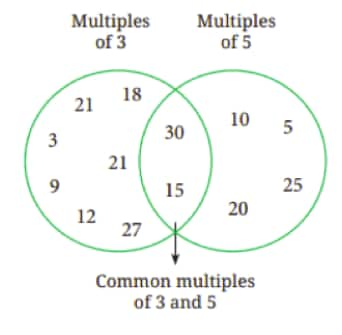
Hint: Imagine playing the game till 30. Draw the figure if the game is played till 60.
Solution:
Yes.
This figure is correct when the game is played till 30.
On the left side, we can see the multiples of 3 till 30 and on the right side, we can see the multiples of 5 till 30.
In the middle, we can see the common multiples of 3 and 5 till 30.
When the game is played till 60.
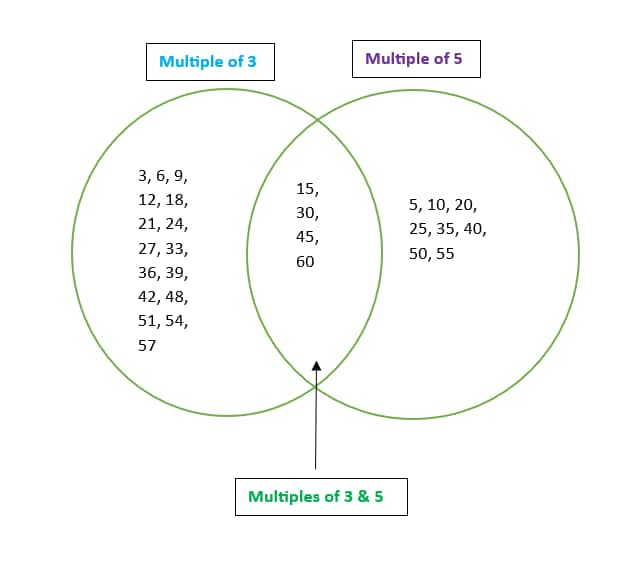
| Prime Time Class 6 Question Answers Page number: 110-111 Number of Questions: 10 |
Question 1: Find all multiples of 40 that lie between 310 and 410.
Solution:
Multiples of 40 are:
40 × 1 = 40
40 × 2 = 80
40 × 3= 120
40 × 4 =160
40 × 5 = 200
40 × 6 = 240
40 × 7 = 280
40 × 8 = 320
40 × 9 = 360
40 × 10 = 400
Hence, the correct answer is 320, 360, and 400.
Question 2: Who am I?
-
I am a number less than 40. One of my factors is 7. The sum of my digits is 8.
-
I am a number less than 100. Two of my factors are 3 and 5. One of my digits is 1 more than the other.
Solution:
a. Numbers less than 40 that are divisible by 7 :
7, 14, 21, 28, 35
Now, let's check whose digits sum to 8:
| Number | Sum of Digits |
| 7 | 7 |
| 14 | 5 |
| 21 | 3 |
| 28 | 10 |
| 35 | 8 |
Hence, the correct answer is 35.
b. If it's divisible by 3 and 5, it's divisible by 15.
Multiples of 15 less than 100 are:
15, 30, 45, 60, 75, 90
Let's check which number "One digit is 1 more than the other".
| Number | Difference between the digits |
| 15 | 4 |
| 30 | 3 |
| 45 | 1 |
| 60 | 6 |
| 75 | 2 |
| 90 | 9 |
Hence, the correct answer is 45.
Question 3: A number for which the sum of all its factors is equal to twice the number is called a perfect number. The number 28 is a perfect number. Its factors are 1, 2, 4, 7, 14, and 28. Their sum is 56, which is twice 28. Find a perfect number between 1 and 10.
Solution:
Factors of 6 are: 1, 2, 3, and 6
Their sum = 1 + 2 + 3 + 6 = 12, which is twice 6.
Hence, the correct answer is 6.
Question 4: Find the common factors of:
-
20 and 28
-
35 and 50
-
4, 8, and 12
-
5, 15, and 25
Solution:
a.
Factors of 20 = 1, 2, 4, 5, 10, 20
Factors of 28 = 1, 2, 4, 7, 14, 28
Common factors = 1, 2, and 4
b.
Factors of 35 = 1, 5, 7, 35
Factors of 50 = 1, 2, 5, 10, 25, 50
Common factors = 1, 5
c.
Factors of 4 = 1, 2, 4
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
Common factors = 1, 2, 4
d.
Factors of 5 = 1, 5
Factors of 15 = 1, 3, 5, 15
Factors of 25 = 1, 5, 25
Common factors = 1, 5
Question 5: Find any three numbers that are multiples of 25 but not multiples of 50.
Solution:
25 × 1 = 25
25 × 2 = 50
25 × 3 = 75
25 × 4 = 100
25 × 5 = 125
Here, 25, 75, 125 are multiples of 25, but not 50.
Hence, the correct answer is 25, 75, and 125.
Question 6: Anshu and his friends play the ‘idli-vada’ game with two numbers, which are both smaller than 10. The first time anybody says ‘idlivada’ is after the number 50. What could the two numbers be which are assigned ‘idli’ and ‘vada’?
Solution:
The two numbers are 7 and 9.
As the first common multiple of 7 & 9 is 63.
Hence, the correct answer is 7 and 9.
Question 7: In the treasure hunting game, Grumpy has kept treasures on 28 and 70. What jump sizes will land on both the numbers?
Solution:
Factors of 28 = 1, 2, 4, 7, 14, 28
Factors of 70 = 1, 2, 5, 7, 10, 14, 35, 70
Common factors = 1, 2, and 7
Hence, the jump sizes 1, 2, and 7 will land on both numbers.
Question 8: In the diagram below, Guna has erased all the numbers except the common multiples. Find out what those numbers could be and fill in the missing numbers in the empty regions.
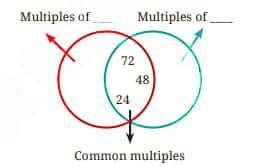
Solution:
Common multiples are 24, 48, and 72
The possible pairs are: (3, 8), (6, 8)
LCM(Least Common Multiple) of all these pairs is 24.
Let's see the diagrams.
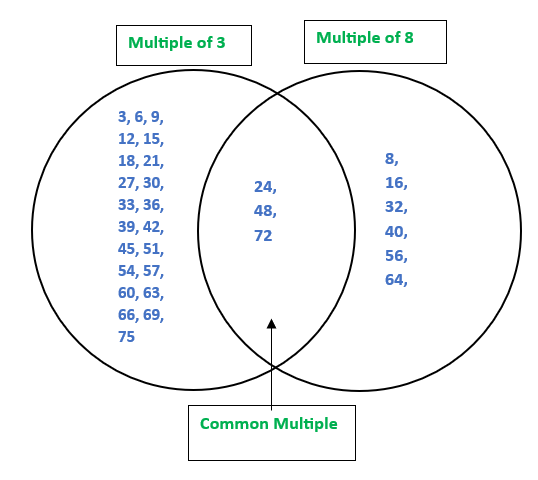
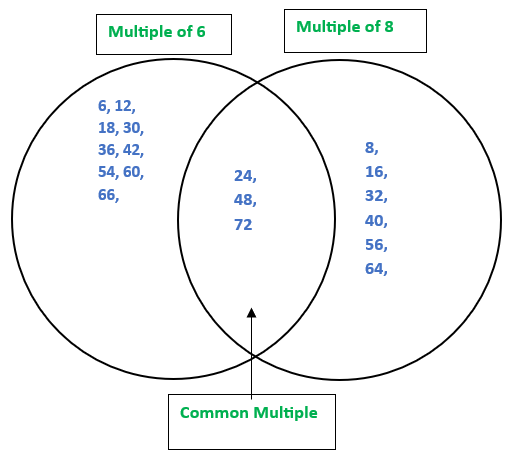
Question 9: Find the smallest number that is a multiple of all the numbers from 1 to 10, except for 7.
Solution:
1
2
3
4 = 2 × 2
5
6 = 2 × 3
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
So, least of multiple (LCM) = 1 × 2 × 3 × 2 × 5 × 3 × 2 = 360
Hence, the correct answer is 360.
Question 10: Find the smallest number that is a multiple of all the numbers from 1 to 10.
Solution:
1
2
3
4 = 2 × 2
5
6 = 2 × 3
7
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
So, least of multiple (LCM) = 1 × 2 × 3 × 2 × 5 × 3 × 2 × 7 = 2520
Hence, the correct answer is 2520.
| Prime Time Class 6 Question Answers Page number: 114-115 Number of Questions: 12 |
Question 1: We see that 2 is a prime and also an even number. Is there any other even prime?
Solution:
Every other even number is divisible by 2, so it will have more than two factors.
All other even numbers are composite.
Hence, the correct answer is “No”.
Question 2: Look at the list of primes till 100. What is the smallest difference between two successive primes? What is the largest difference?
Solution:
The differences between successive primes till 100:
-
3 - 2 = 1
-
5 - 3 = 2
-
7 - 5 = 2
-
11 - 7 = 4
-
13 - 11 = 2
-
17 - 13 = 4
-
19 - 17 = 2
-
23 - 19 = 4
-
29 - 23 = 6
-
31 - 29 = 2
-
37 - 31 = 6
-
41 - 37 = 4
-
43 - 41 = 2
-
47 - 43 = 4
-
53 - 47 = 6
-
59 - 53 = 6
-
61 - 59 = 2
-
67 - 61 = 6
-
71 - 67 = 4
-
73 - 71 = 2
-
79 - 73 = 6
-
83 - 79 = 4
-
89 - 83 = 6
-
97 - 89 = 8
$\therefore$ The smallest possible difference between any two primes till 100 is 1.
And the largest possible difference between any two primes till 100 is 8.
Question 3: Are there an equal number of primes occurring in every row in the table on the previous page? Which decades have the least number of primes? Which have the most number of primes?
Solution:
No, there is no equal number of primes occurring in every row in the table.
In 91-100, there is only one prime number, which is the least number of primes in a decade.
In 1-10 and 11-20, there are 4 prime numbers each, which is the largest number of primes in a decade.
Question 4: Which of the following numbers are prime: 23, 51, 37, 26?
Solution:
Factors of 23 = 1, 23
Factors of 51 = 1, 3, 17, 51
Factors of 37 = 1, 37
Factors of 26 = 1, 2, 13, 26
Hence, 23 and 37 are prime numbers.
Question 5: Write three pairs of prime numbers less than 20 whose sum is a multiple of 5.
Solution:
First pair:
2 + 3 = 5 (5 is a multiple of 5 )
Second pair:
7 + 13 = 20 (20 is a multiple of 5 )
Third pair:
11 + 19 = 30 (30 is a multiple of 5)
Question 6: The numbers 13 and 31 are prime numbers. Both these numbers have the same digits 1 and 3. Find such pairs of prime numbers up to 100.
Solution:
List of prime numbers till 100:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
Such pairs are: (17, 71), (37, 73), (79, 97)
Question 7: Find seven consecutive composite numbers between 1 and 100.
Solution:
List of prime numbers till 100:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
As we can see, the gap between the two prime numbers 89 and 97 is 8.
So, in between, there are 7 consecutive composite numbers: 90, 91, 92, 93, 94, 95, 96.
Question 8: Twin primes are pairs of primes having a difference of 2. For example, 3 and 5 are twin primes. So are 17 and 19. Find the other twin primes between 1 and 100.
Solution:
List of prime numbers till 100:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
The twin primes between 1 and 100 are:
5 and 7, 11 and 13, 29 and 31, 41 and 43, 59 and 61, 71 and 73
Question 9: Identify whether each statement is true or false.
Explain.
a. There is no prime number whose unit's digit is 4.
b. A product of primes can also be prime.
c. Prime numbers do not have any factors.
d. All even numbers are composite numbers.
e. 2 is a prime, and so is the next number, 3. For every other prime, the next number is composite.
Solution:
a. Prime numbers generally end with 1, 3, 7, or 9 (except for 2 and 5).
A number ending with 4 would be even and greater than 2, so it would be divisible by 2.
Hence, it can't be a prime number.
∴ This statement is True.
b. If we multiply two primes, the result is a composite number, not a prime.
Example: 2 × 3 = 6; 11 × 13 = 143; 5 × 7 = 35 and so on.
A prime number has only two factors: 1 and itself.
∴ This statement is not True.
c. A prime number has two factors: 1 and itself.
∴ This statement is not True.
d. 2 is an even number and also a prime number.
All even numbers greater than 2 are composite.
∴ This statement is not True.
e. After 2 and 3, the next number after any prime is always composite.
Example: 7 and 8, 11 and 12, 13 and 14, and so on.
No two primes after 2 and 3 are consecutive integers.
∴ This statement is True.
Question 10: Which of the following numbers is the product of exactly three distinct prime numbers: 45, 60, 91, 105, 330?
Solution:
45 = 3 × 3 × 5
60 = 2 × 2 × 3 × 5
91 = 7 × 13
105 = 3 × 5 × 7
330 = 2 × 3 × 5 × 11
As we can see, the product of three distinct primes, 3, 5, and 7, is 105.
Hence, the correct answer is 105.
Question 11: How many three-digit prime numbers can you make using each of 2, 4 and 5 once?
Solution:
List all possible numbers using 2, 4, and 5 exactly once:
-
245 (It is not a prime number)
-
254 (It is not a prime number)
-
425 (It is not a prime number)
-
452 (It is not a prime number)
-
524 (It is not a prime number)
-
542 (It is not a prime number)
As we can see, none of the six numbers formed using the digits 2, 4, and 5 are prime numbers.
Hence, the correct answer is 0.
Question 12: Observe that 3 is a prime number, and 2 × 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Solution:
Yes, there are other primes for which doubling and adding 1 gives another prime.
These types of examples are:
2 × 2 + 1 = 5 (Prime number)
2 × 5 + 1 = 11 (Prime number)
2 × 11 + 1 = 23 (Prime number)
2 × 23 + 1 = 47 (Prime number)
2 × 29 + 1 = 59 (Prime number)
| Prime Time Class 6 Question Answers Page number: 120 Number of Questions: 5 |
Question 1: Find the prime factorisations of the following numbers:
64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Solution:
Prime factorization of 64 = 2 × 2 × 2 × 2 × 2 × 2
Prime factorization of 104 = 2 × 2 × 2 × 13
Prime factorization of 105 = 3 × 5 × 7
Prime factorization of 243 = 3 × 3 × 3 × 3 × 3
Prime factorization of 320 = 2 × 2 × 2 × 2 × 2 × 2 × 5
Prime factorization of 141 = 3 × 47
Prime factorization of 1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
Prime factorization of 729 = 3 × 3 × 3 × 3 × 3 × 3
Prime factorization of 1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Prime factorization of 1331 = 11 × 11 × 11
Prime factorization of 1000 = 2 × 2 × 2 × 5 × 5 × 5
Question 2: The prime factorisation of a number has one 2, two 3s, and one 11. What is the number?
Solution:
The required number = 2 × 3 × 3 × 11 = 198
Hence, the correct answer is 198.
Question 3: Find three prime numbers, all less than 30, whose product is 1955.
Solution:
1955 = 5 × 17 × 23
Hence, the correct answers are 5, 17, and 23.
Question 4: Find the prime factorisation of these numbers without multiplying first:
a. 56 × 25
b. 108 × 75
c. 1000 × 81
Solution:
a. 56 × 25 = 2 × 2 × 2 × 7 × 5 × 5
b. 108 × 75 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
c. 1000 × 81 = 2 × 2 × 2 × 5 × 5 × 5 × 3 × 3 × 3 × 3
Question 5: What is the smallest number whose prime factorisation has:
a. Three different prime numbers?
b. Four different prime numbers?
Solution:
a. The smallest three prime numbers are: 2, 3, 5
So, the number is: 2 × 3 × 5 = 30
b. The smallest four prime numbers are: 2, 3, 5, 7
So, the number is: 2 × 3 × 5 × 7 = 210
| Prime Time Class 6 Question Answers Page number: 122 Number of Questions: 4 |
Question 1: Are the following pairs of numbers co-prime? Guess first and then use prime factorisation to verify your answer.
a. 30 and 45
b. 57 and 85
c. 121 and 1331
d. 343 and 216
Solution:
a. 30 and 45 are not co-prime.
30 = 2 × 3 × 5
45 = 3 × 3 × 5
As 3 and 5 are common factors between 30 and 45.
b. 57 and 85 are co-prime.
57 = 3 × 19
85 = 5 × 17
As there is no common factor between 57 and 85.
c. 121 and 1331 are not co-prime.
121 = 11 × 11
1331 = 11 × 11 × 11
As 11 is a common factor between 121 and 1331.
Question 2: Is the first number divisible by the second? Use prime factorisation.
a. 225 and 27
b. 96 and 24
c. 343 and 17
d. 999 and 99
Solution:
a. 225 = 5 × 5 × 3 × 3
27 = 3 × 3 × 3
If we divide 225 by 27, we get $\frac{5 \times 5}{3}$, which is not an integer. $\therefore 225$ is not divisible by 27.
b. 96 = 2 × 2 × 2 × 2 × 2 × 3
24 = 2 × 2 × 2 × 3
If we divide 96 by 24, we get 4, which is an integer.
∴ 96 is divisible by 24.
c. 343 = 7 × 7 × 7
17 = 1 × 17
If we divide 343 by 17, we get $\frac{343}{17}$, which is not an integer.
$\therefore 343$ is not divisible by 17.
d. 999 = 3 × 3 × 3 × 37
99 = 3 × 3 × 11If we divide 999 by 99 , we get $\frac{3 \times 37}{11}$, which is not an integer.
$\therefore 999$ is not divisible by 99.
Question 3: The first number has prime factorisation 2 × 3 × 7, and the second number has prime factorisation 3 × 7 × 11. Are they co-prime? Does one of them divide the other?
Solution:
The first number has prime factorisation 2 × 3 × 7,
And the second number has prime factorisation 3 × 7 × 11.
So, they are not co-prime as there are two common factors, 3 and 7.
2nd number is the bigger number, and it can’t be completely divided by the 1st number as there are uncommon factors, 11 and 2.
Question 4: Guna says, “Any two prime numbers are co-prime?”. Is he right?
Solution:
Co-prime numbers are two numbers that have no common factors other than 1.
Prime numbers are numbers that have only two factors: 1 and itself.
So, Guna is right.
Example: 11 and 13, 13 and 17, and so on.
|
Prime Time Class 6 Question Answers |
Question 1: 2024 is a leap year (as February has 29 days). Leap years occur in the years that are multiples of 4, except for those years that are evenly divisible by 100 but not 400.
a. From the year you were born till now, which years were leap years?
b. From the year 2024 till 2099, how many leap years are there?
Solution:
a. Let us say I was born in 1995. From 1995 to 2025, leap years are:
1996, 2000, 2004, 2008, 2012, 2016, 2020, 2024 [8 leap years]
b. From the year 2024 till 2099, leap years are:
2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076, 2080, 2084, 2088, 2092, 2096 [Total 19 leap years]
Hence, the correct answer is 19
Question 2: Find the largest and smallest 4-digit numbers that are divisible by 4 and are also palindromes.
Solution:
A palindrome number is a number that remains the same when its digits are reversed.
The largest 4-digit palindrome is 9999. But if the unit digit is 9, the number is not divisible by 4.
Let's check numbers whose unit digit is 8.
-
$8998 \rightarrow$ Not a palindrome.
-
$8888 \rightarrow$ Last two digits $=88 \rightarrow 88 \div 4=22$ [Divisible]
∴ The largest 4-digit palindrome divided by 4 is 8888.
The smallest 4-digit palindrome is 1001. But if the unit digit is 1, the number is not divisible by 4.
Let's check numbers whose unit digit is 2.
-
$2002 \rightarrow 2 \div 4=0.5$ (Not divisible)
-
$2112 \rightarrow 12 \div 4=3$ [Divisible]
∴ The smallest 4-digit palindrome divided by 4 is 2112.
Question 3: Explore and find out if each statement is always true, sometimes true or never true. You can give examples to support your reasoning
a. Sum of two even numbers gives a multiple of 4.
b. Sum of two odd numbers gives a multiple of 4.
Solution:
a. This statement is sometimes true.
When two even numbers are added, the sum is always an even number. However, whether the sum is a multiple of 4 depends on the specific even numbers being added.
- Example 1: 2 + 4 = 6 (which is not a multiple of 4 )
- Example 2: 4 + 8 = 12 (which is a multiple of 4 )
- Example 3: 6 + 10 = 16 (which is a multiple of 4 )
b. This statement is sometimes true. When two odd numbers are added, the result is always an even number, but not necessarily a multiple of 4.
- Example 1: 1 + 3 = 4 (which is a multiple of 4 )
- Example 2: 1 + 5 = 6 (which is not a multiple of 4 )
- Example 3: 7 + 9 = 16 (which is a multiple of 4 )
- Example 4: 3 + 11 = 14 (which is not a multiple of 4 )
Question 4: Find the remainders obtained when each of the following numbers are divided by:
(a) 10, (b) 5, (c) 2.
78, 99, 173, 572, 980, 1111, 2345
Solution:
|
Number |
Remainder when Divided by 10 |
Remainder when Divided by 5 |
Remainder when Divided by 2 |
|
78 |
8 |
3 |
0 |
|
99 |
9 |
4 |
1 |
|
173 |
3 |
3 |
1 |
|
572 |
2 |
2 |
0 |
|
980 |
0 |
0 |
0 |
|
1111 |
1 |
1 |
1 |
|
2345 |
5 |
0 |
1 |
Question 5: The teacher asked if 14560 is divisible by all of 2, 4, 5, 8 and 10. Guna checked for the divisibility of 14560 by only two of these numbers and then declared that it was also divisible by all of them. What could those two numbers be?
Solution:
- The last digit is 0, so 14560 is divisible by 2, 5, and 10.
- The last three digits are 560, and 560 is divisible by 8, so 14560 is divisible by 8.
Guna checked only the divisibility by 5 and 8, which 5 ensures divisibility by 10, and Divisibility by 8 ensures divisibility by 2 and 4 (2 × 4 = 8).
Hence, the correct numbers are 5 and 8.
Question 6: Which of the following numbers are divisible by all of 2, 4, 5, 8 and 10:
572, 2352, 5600, 6000, 77622160.
Solution:
LCM of 2, 4, 5, 8, and 10 = 40
So, if the number is divisible by 40, then it is divisible by all these numbers.
Also, if a number is divisible by 5 and 8, it is divisible by 40.
Now, the Divisibility rule of 5: A number is divisible by 5 if its last digit is 0 or 5.
Divisibility rule of 8: A number is divisible by 8 if the last three digits form a number divisible by 8.
572: Last digit is not 0 or 5. So, it is not completely divisible by 40.
2352: Last digit is not 0 or 5. So, it is not completely divisible by 40.
5600: Last digit is 0, and 600 is divisible by 8. So it is completely divisible by 40.
6000: Last digit is 0, and 000 is divisible by 8. So, it is completely divisible by 40.
77622160: Last digit is 0, and 160 is divisible by 8. So, it is completely divisible by 40.
Alternate method:
|
Number |
Divisibility by 2 |
Divisibility by 4 |
Divisibility by 5 |
Divisibility by 8 |
Divisibility by 10 |
Divisible by All (2, 4, 5, 8, 10)? |
|
572 |
Yes |
Yes |
No |
No |
No |
No |
|
2352 |
Yes |
Yes |
No |
Yes |
No |
No |
|
5600 |
Yes |
Yes |
Yes |
Yes |
Yes |
Yes |
|
6000 |
Yes |
Yes |
Yes |
Yes |
Yes |
Yes |
|
77622160 |
Yes |
Yes |
Yes |
Yes |
Yes |
Yes |
Question 7: Write two numbers whose product is 10000. The two numbers should not have 0 as the unit's digit.
Solution:
Prime factorization of 10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5
So, the two numbers can be:
2 × 2 × 2 × 2 = 16
5 × 5 × 5 × 5 = 625
Hence, the unit digit is not zero.
NCERT Prime Time Class 6 Maths Chapter 5 - Topics
Topics you will learn in NCERT Class 6 Maths Chapter 5 Prime Time include:
5.1 Common Multiples and Common Factors
5.2 Prime Numbers
5.3 Co-prime Numbers for Safekeeping Treasures
5.4 Prime Factorisation
5.5 Divisibility Tests
Class 6 Maths Chapter 5 Prime Time solutions: Extra Question
Question:
Is 156 divisible by 3 and 4? Explain using divisibility rules.
Solution:
We know that a number is divisible by 3 if the sum of its digits is divisible by 3.
For 156, the sum of the digits is: 1+5+6=12
Since 12 is divisible by 3, 156 is divisible by 3.
Also, A number is divisible by 4 if the last two digits form a number that is divisible by 4.
The last two digits of 156 are 56.
Since 56 is divisible by 4 ( $56 \div 4=14$ ), 156 is divisible by 4.
Hence, 156 is divisible by both 3 and 4.
NCERT Solutions for Class 6 Maths Chapter 5 Prime Time: Notes
Careers360 has prepared these Class 6 Prime Time Notes to make your revision smoother and faster. Additionally, these notes will help students understand the class 6 maths Prime Time solutions and solve them independently from next time.
Prime Numbers
Prime numbers are those numbers in mathematics that have only two factors. For example, primes 2, 11, 13, 17, etc.
Factors of a prime number: The number itself and 1.
Prime numbers from 1 to 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Composite Numbers
Composite numbers are defined as those that have more factors apart from 1 and the number itself. The first few composite numbers are—4, 6, 8, 9, 14, 15, 12, 20, etc.
Note: The number 1 is neither a prime nor a composite number.
Method to find prime numbers:
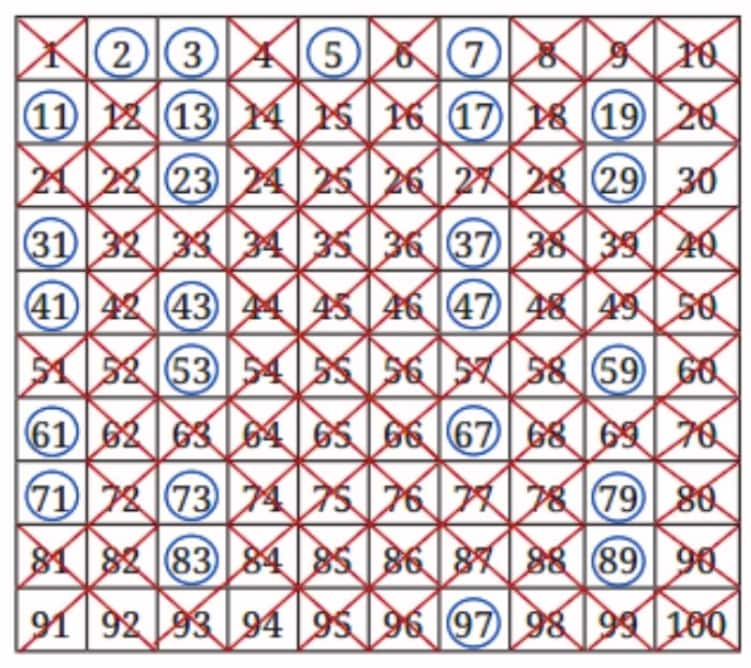
Sieve of Eratosthenes:
.jpg)
Step 1: We cancel the number 1 as it belongs to neither category.
Step 2: Next, we circle 2, and subsequently cross out all multiples of 2.
Step 3: Now, we circle 3 and then cross out all the multiples of 3 after that.
Step 4: We continue this process till all the numbers in the list are either circled or crossed out.
We hence observe that all the circled numbers are prime numbers and all the crossed-out numbers, other than 1, are composite numbers. This is the Sieve of Eratosthenes.
Prime Factorisation
This method helps us to break a number into its factors to check whether it is prime or not.
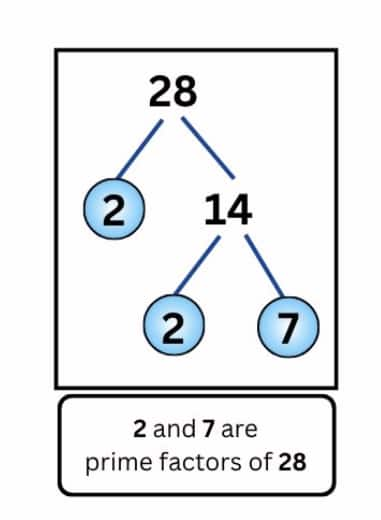
For example, check whether 56 and 63 are co-prime.
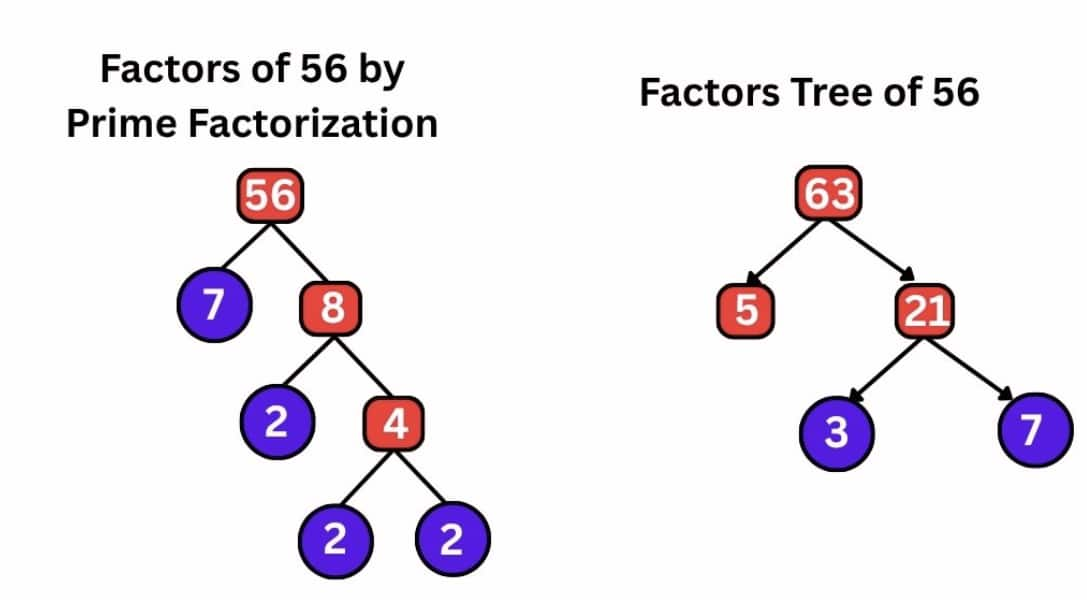
56 can be written as 14 × 4 and 63 as 21 × 3. We observe carefully that there are no common factors initially.
But we can also write 56 as 7 × 8 and 63 as 9 × 7. We see that 7 is a factor of both numbers, so they are not co-prime. And hence composite.
56 = 2 × 2 × 2 × 7. All the factors appearing here, 2 and 7, are prime numbers. So, we cannot divide them further.
In conclusion, we have written 56 as a product of prime numbers.
This is called the prime factorisation of 56. The individual factors are called prime factors. For example, the prime factors of 56 are 2 and 7.
Every number greater than 1 has a prime factorisation.
Note: The order of prime factors does not matter while writing, since multiplication is commutative.
Prime factorisation of a product of two numbers
When we find the prime factorisation of a number, we first write it as a product of two factors. For example, 100 = 10 × 10. Next, we find the prime factorisation of each of the factors. In the above example, 10 = 2 × 5 and 10 = 2 × 5.
The prime factorisation of the original number is obtained by putting these together.
100 = 2 × 2 × 5 × 5
Example: Find out if 168 is divisible by 12? First, we find the prime factorisations of both:
168 = 2 × 2 × 2 × 3 × 7 and 12 = 2 × 2 × 3
Since we can multiply in any order, it is now clear that,
168 = 2 × 2 × 3 × 2 × 7 = 12 × 14
Therefore, 168 is divisible by 12.
Divisibility tests
Divisibility by 10
Is 8560 divisible by 10?
We list the first few multiples of 10 are: 10, 20, 30, 40, and so on.
Hence, we can conclude and say that Numbers that are divisible by 10 are those that end with ‘0’. Eg 100,10
Divisibility by 5
Following the similar trend seen above and listing multiples of 5, we can say that Numbers that are divisible by 5 are those that end with either a ‘0’ or a ‘5’. Eg 25,30
Divisibility by 2
Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, etc.
We observe that numbers that are divisible by 2 are those that end with ‘0’, ‘2’, ‘4, ‘6’ or ‘8’. Means they have an even digit at one's place.
Divisibility by 4
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, and so on
Results :
1. We see the last 2 digits of a number to check its divisibility by 4. If so, then it passes the test.
2. In case the original number is divisible by 4, then the number formed by the last two digits is also divisible by 4. For example, 512, 4824, 7996
Divisibility by 8
1. We see only the last three digits to check this test. If they are divisible by 8, they pass the test.
2. When the original number is divisible by 8, then the number formed by the last three digits is divisible by 8. For example, 936, 4528, 8976
Class 6 Maths Chapter 5 Prime Time Solutions: Points to Remember
Check the following important points to understand and solve Class 6 Maths Chapter 5 Prime Time question answers effectively.
Prime Numbers: Prime numbers are numbers that are divisible only by themselves and 1.
Composite Numbers: Composite numbers are numbers that are divisible not only by themselves and 1 but also by certain numbers.
Prime Factorisation: Prime factorisation is a method of expressing numbers as a product of prime numbers.
Why are Class 6 Maths Chapter 5 Prime Time question answers important?
As the name of the chapter suggests, this chapter focuses on some important concepts of number systems, such as prime numbers, composite numbers, factors and multiples. These are the building blocks of number systems in higher classes. Here are some more points on why we should practice Class 6 Maths Prime time question answers efficiently.
- These question answers will help a student to understand an important concept for this class, as well as higher classes: Divisibility rules.
- Also, this chapter becomes fundamental to learn the basics of some important chapters of algebra and arithmetic in higher classes, such as HCF, LCM, and prime factorisation.
- Regular practice of these questions will help to improve a student’s accuracy as well as time management skills during the exam.
NCERT Class 6 Maths Chapter Wise Solutions
We at Careers360 compiled all the NCERT class 6 Maths solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and the NCERT Syllabus
Students can also check the NCERT Books and the NCERT Syllabus for Class 6 here:
Frequently Asked Questions (FAQs)
Prime factorisation helps to find the HCF and LCM of numbers easily and forms the basis for simplifying fractions.
Prime factorisation is the process of expressing a number as the product of its prime factors.
Example: 60 = 2 × 2 × 3 × 5
Factors are numbers that divide a given number exactly.
Multiples are obtained by multiplying a number by whole numbers.
Yes, every number is both a factor and a multiple of itself.
For example, 6 is a factor of 6 as 6/6 = 1
Also, 6 is a multiple of 6 as 6 × 1 = 6
Yes, free downloadable PDFs are available on various educational websites, such as Careers360, for practice and revision.
A prime number is a number greater than 1 that has exactly two factors – 1 and itself.
Prime numbers are the building blocks of numbers, as every number can be expressed in terms of prime factors.
The smallest prime number is 2, and it is also the only even prime number.
This chapter covers topics such as:
- Prime numbers
- Co-prime numbers
- Prime factorisation
- Divisibility tests
HCF (Highest Common Factor) is the largest number that divides two or more numbers.
LCM (Lowest Common Multiple) is the smallest common multiple of two or more numbers.
These are used in real-life problems like sharing items and arranging events.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
