NCERT Solutions for Class 6 Maths Chapter 8 - Playing with Constructions
With just a compass and a ruler, one can create magic and draw lines, angles, and shapes, bringing them alive when someone is playing with constructions. In the NCERT Class 6 Maths Chapter 8, students will learn about “Playing with constructions” as it is the entry path to geometry. This chapter focuses more on drawing geometrical figures with a compass and ruler. Various important topics such as Constructing Squares and Rectangles, exploring their diagonals, and drawing points Equidistant from two given points are discussed in Chapter 8 of Class 6. The primary benefit of NCERT Solutions for Class 6 Maths is that they provide clear explanations, making learning simpler and more effective.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Download Free PDF
- NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Exercise Questions
- NCERT Playing with Constructions Class 6 Maths Chapter 8: Topics
- Class 6 Maths Chapter 8 Playing with Constructions solutions: Extra Question
- NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Notes
- NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Points to Remember
- Why are Class 6 Maths Chapter 8 Playing with Constructions question answers important?
- NCERT Solutions for Class 6 Mathematics Chapter-wise
- NCERT Books and NCERT Syllabus

Through the art of construction, we shape not only important geometric figures but also our understanding of space and form. These NCERT Solutions for Class 6 are curated by experienced subject matter experts of Careers360. All the solutions are well-detailed and explained in a student-friendly manner. Many teachers recommend NCERT Solutions because they closely match the exam pattern. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Download Free PDF
Careers360 brings you Class 6 Maths Chapter 8 Playing with Constructions NCERT solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Exercise Questions
Given below are the detailed Class 6 Maths Chapter 8 Playing with Constructions question answers given in the textbook.
|
Playing with Constructions Class 6 Question Answers |
Figure it Out
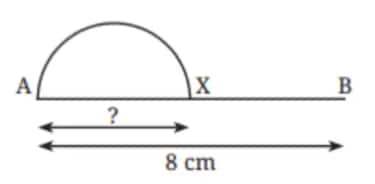
Q1. What radius should be taken in the compass to get this half circle? What should be the length of AX?
Answer:
Length of AB = 8 cm
X is the mid-point of AB, i.e. AX = XB
Length of AX = $\frac{AB}{2}$ = $\frac{8}{2}$ = 4 cm
Radius of the half circle = $\frac{AX}{2}$ = $\frac{4}{2}$ = 2 cm.
Q2. Take a central line of a different length and try to draw the wave on it.
Answer:
Step 1. Draw a central line AB = 10 cm

Step 2. Since half of AB is 5 cm, mark a point X on AB such that AX = XB = 5 cm.

Step 3. Mark a point C on AX such that AC = CX = 2.5 cm. Mark another point D on XB such that XD = DB =2.5 cm.

Step 4. With C as the centre and radius equal to AC, draw a semicircle above the line AB. Again, with D as centre and radius equal to XD, draw another semicircle below the line AB.
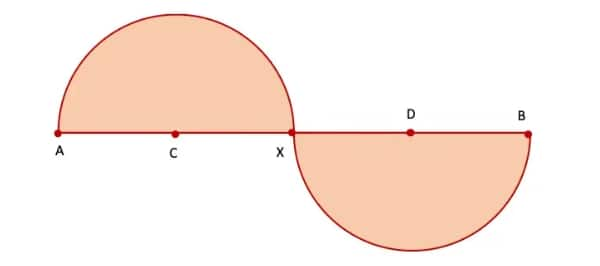
Step 5. The resultant figure is the required wavy wave with a central line of length 10 cm.
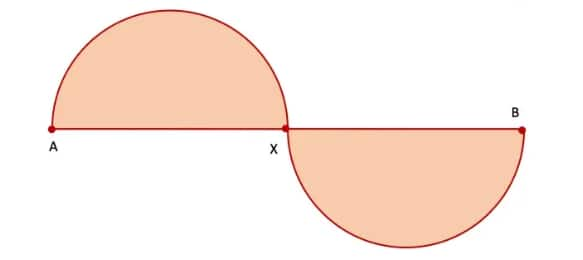
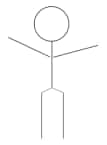
Q3. Try to recreate the figure where the waves are smaller than a half circle (as appearing in the neck of the figure, ‘A Person’). The challenge here is to get both the waves to be identical. This may be tricky!
Answer:
Step 1. Draw a central line AB = 8 cm

Step 2. Since half of AB is 4 cm, mark a point X on AB such that AX = XB = 4 cm

Step 3. Mark a point C on AX such that AC = CX = 2 cm. Mark another point D on XB such that:
XD = DB = 2 cm.

Step 4. Draw perpendiculars at points C and D.
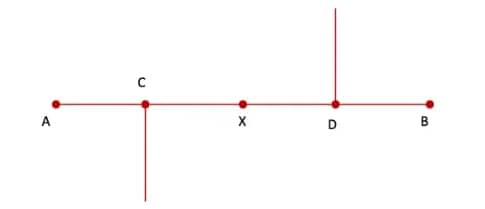
Step 5. Mark point E on a perpendicular at C and mark point F on a perpendicular at D such that
CE = DF = 1 cm. Join AE and BF.
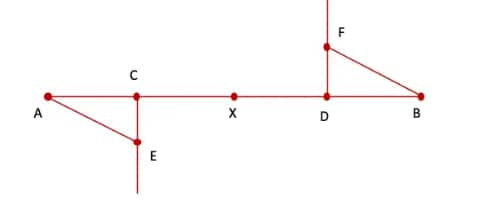
Step 6. With E as centre and radius equal to AE, draw an arc from A to X. Also, with F as the centre and radius equal to BF, draw another arc from B to X.
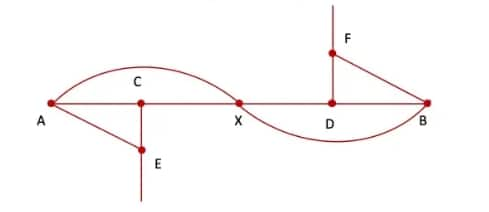
Step 7. Erase all the extra lines and marked points from the above figure; the resultant figure is the required wavy wave.
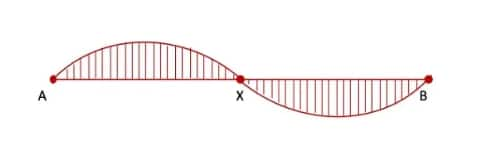
| Playing with Constructions Class 6 Question Answers Page number: 194 Number of Questions: 3 |
Figure it Out
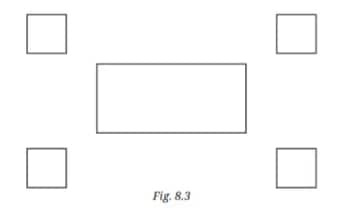
Q1. Draw the rectangle and four squares configuration (shown in Fig. 8.3) on a dot paper. What did you do to recreate this figure so that the four squares are placed symmetrically around the rectangle? Discuss with your classmates.
Answer:
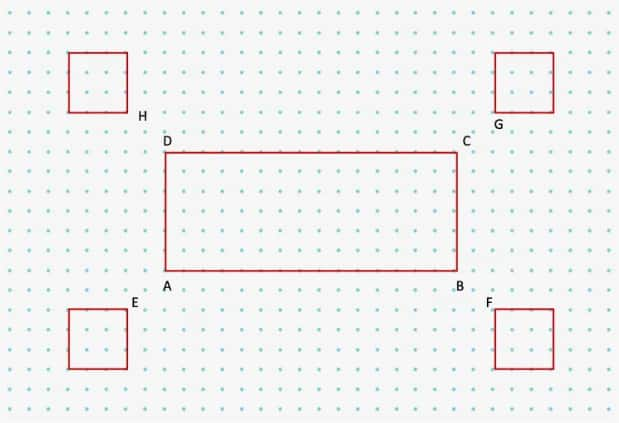
(i) Take a dot on dot-paper and mark it as A. Starting from A, move 15 dots to the right and mark the 15th dot as point B.
(ii) Starting from point B, move 6 dots upwards and mark the 6th dot as point C. Similarly, starting from point A, move 6 dots upwards and mark the 6th dot as point D.
(iii) Join points A to B, B to C, C to D, and D to A.
(iv) Take points E, F, G, and H on the dot paper as shown in the figure.
(v) At points E, F, G, and H, draw four squares, each with sides consisting of 4 dots, as shown in the figure.
(vi) The resultant figure is the required rectangle and square configuration on a dot paper.
Q2. Identify if there are any squares in this collection. Use measurements if needed.
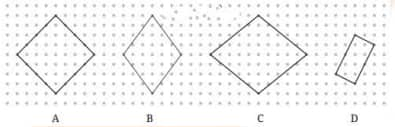
Think: Is it possible to reason out if the sides are equal or not, and if the angles are right or not, without using any measuring instruments in the above figure? Can we do this by only looking at the position of corners in the dot grid?
Answer:
(i) In Fig. A, each side has an equal number of dots, and each angle, when measured with a protractor, is 90°. So fig. A is a square.
(ii) In Fig. B, each side has an equal number of dots, but the angles, when measured with a protractor, are not 90°. Therefore, Fig. B cannot be a square, as a square has all its angles equal to 90°.
(iii) In Fig. C, each side has an equal number of dots, and each angle, when measured with a protractor, is 90°. So, fig. C is a square.
(iv) In Fig. D, not all sides have an equal number of dots, though each angle, when measured with a protractor, is 90°. Therefore, Fig. D cannot be a square, as a square has all sides equal.
Q3. Draw at least 3 rotated squares and rectangles on a dot grid. Draw them such that their corners are on the dots. Verify if the squares and rectangles that you have drawn satisfy their respective properties.
Answer:
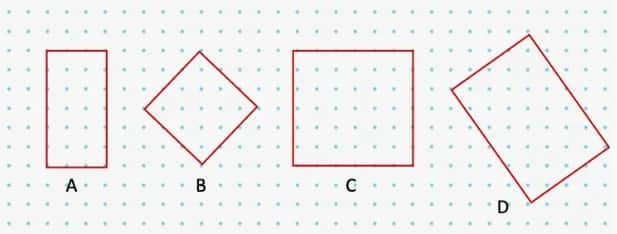
In Fig. A, one pair of sides has 4 dots, while the other pair has 7 dots. Additionally, all the angles measure 90°. Therefore, Fig. A is a rectangle.
In Fig. B, all sides have 4 dots each, and all angles are 90°. Therefore, Fig. B is a square.
In Fig. C, all sides have 7 dots each, and all angles are 90°. Therefore, Fig. C is a square.
In Fig. D, one pair of sides has 5 dots, while the other pair has 8 dots. Additionally, all the angles measure 90°. Therefore, Fig. D is a rectangle.
Hence, Figures B and C are squares while Figures A and D are rectangles satisfying their respective properties.
| Playing with Constructions Class 6 Question Answers Page number: 197 Number of Questions: 3 |
Construct
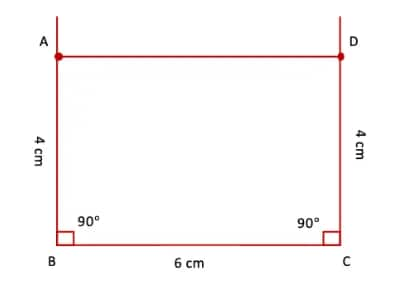
Q1. Draw a rectangle with sides of length 4 cm and 6 cm. After drawing, check if it satisfies both the rectangle properties.
Answer:
Steps of construction:
(i) Draw a line segment BC = 6 cm.
(ii) At B and C, draw perpendiculars with the help of a protractor.
(iii) Mark point A on the perpendicular at point B and point D on the perpendicular at point C such that BA = 4 cm and CD = 4 cm.
(iv) Join AD.
(v) Verify with the help of a ruler that AB = 6 cm.
Also, with the help of a protractor, verify that ∠A = ∠D = 90°.
(vi) Thus, we have
AB = DC = 4 cm, BC =AD = 6 cm and ∠A = ∠B = ∠C = ∠D = 90°
Hence, ABCD is the required rectangle satisfying both the properties of a rectangle.
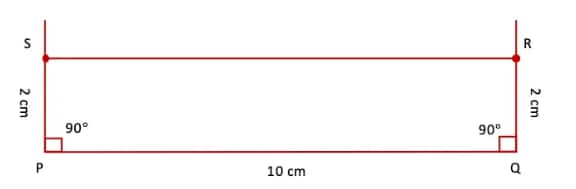
Q2. Draw a rectangle of sides 2 cm and 10 cm. After drawing, check if it satisfies both the rectangle properties.
Answer:
Steps of construction:
(i) Draw a line segment PQ = 10 cm.
(ii) At P and Q, draw perpendiculars with the help of a protractor.
(iii) Mark point S on the perpendicular at P and point R on the perpendicular at Q such that PS = 2 cm and QR = 2 cm.
(iv) Join SR.
(v) Verify with the help of a ruler that SR = 10 cm.
Also, with the help of a protractor, verify that ∠S = ∠R = 90°.
(vi) Thus, we have
PQ = SR = 10 cm, PS = QR = 2 cm and ∠P = ∠Q = ∠R = ∠S = 90°.
Hence, PQRS is the required rectangle satisfying both the properties of a rectangle.
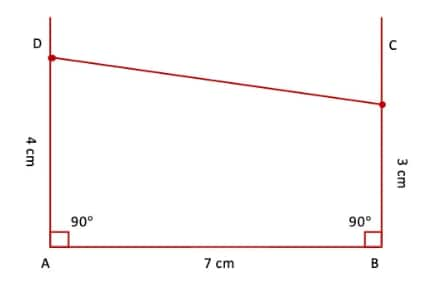
Q3. Is it possible to construct a 4-sided figure in which-
-
All the angles are equal to 90º, but
-
Opposite sides are not equal?
Answer:
(i) Draw a line segment AB = 7 cm.
(ii) At A and B, draw perpendiculars with the help of a protractor.
(iii) Take two points C and D on the two perpendiculars such that AD = 4 cm and BC = 3 cm.
(iv) Join DC.
Since the opposite sides AD and BC are not equal, it is found that neither ∠D nor ∠C is 90°. Hence, we conclude that it is not possible to draw a four-sided figure with all angles equal to 90° when opposite sides are not equal.
| Playing with Constructions Class 6 Question Answers Page number: 211 Number of Questions: 4 |
Construct
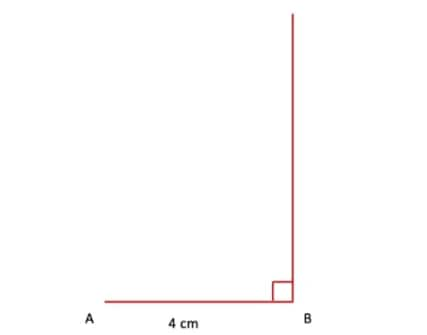
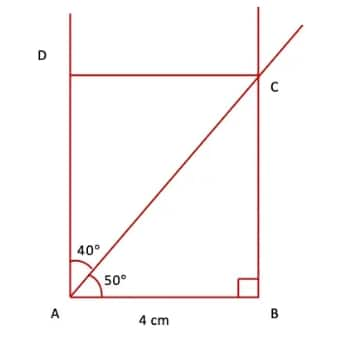
Q1. Construct a rectangle in which one of the diagonals divides the opposite angles into 50° and 40°.
Answer:
Step 1. Draw a line segment AB = 4 cm. At point B, draw a line perpendicular to AB.
Step 2. At point A, draw a line AC making an angle of 50° with AB and intersecting the perpendicular drawn in Step(1) at point C.
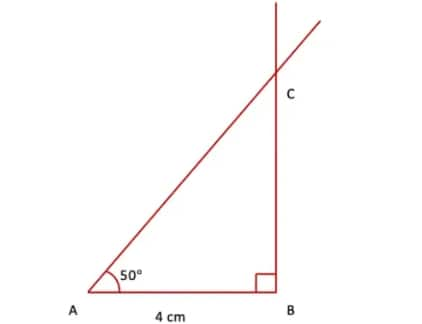
Step 3. At point A, draw a line perpendicular to AB and parallel to BC. Mark a point D on this perpendicular such that AD = BC. Join CD. Therefore, ABCD is the required rectangle in which diagonal AC divides ∠A such that ∠CAB = 50° and ∠DAC = 40°.
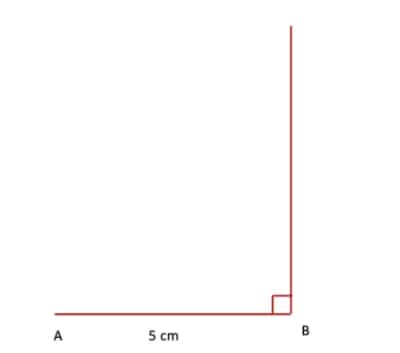
Q2. Construct a rectangle in which one of the diagonals divides the opposite angles into 45° and 45°. What do you observe about the sides?
Answer:
Step 1. Draw a line segment AB = 5 cm. At point B, draw a line perpendicular to AB.
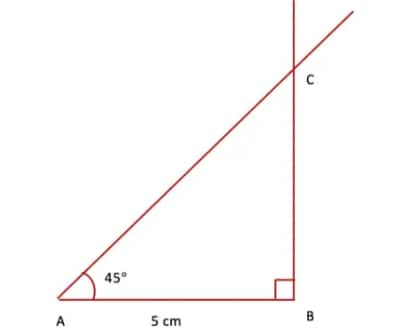
Step 2. At point A, draw a line AC making an angle of 45° with AB and intersecting the perpendicular line drawn in Step(1) at point C.
Step 3. At point A, draw a line perpendicular to AB, parallel to BC. Mark a point D on this perpendicular such that AD = BC. Join CD.
Therefore, ABCD is the required rectangle in which diagonal AC divides ∠A such that ∠CAD = ∠CAB = 45°.
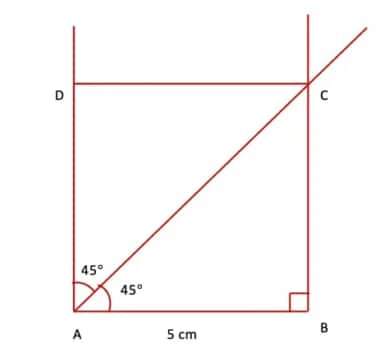
Here, the sides of the rectangle obtained are equal in length, making the resultant figure a square.
Q3. Construct a rectangle one of whose sides is 4 cm and the diagonal is of length 8 cm.
Answer:
Step 1. Draw a line segment AB = 4 cm. Draw perpendicular lines at points A and B.
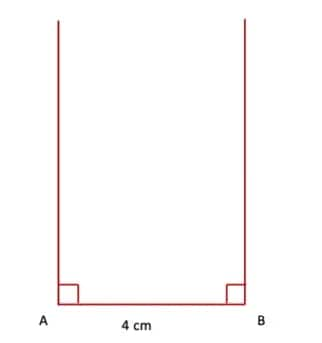
Step 2. With A as the centre and radius equal to 8 cm, draw an arc intersecting the perpendicular at B. Similarly, with B as the centre and radius equal to 8 cm, draw an arc intersecting the perpendicular at A.
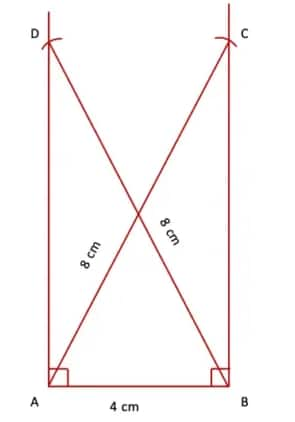
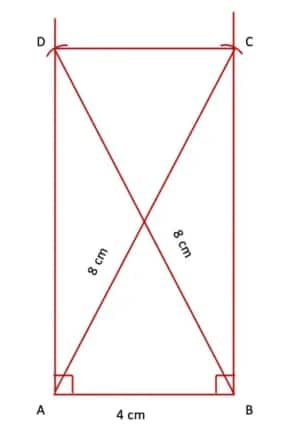
Step 3. Join points D and C.
ABCD is the required rectangle.
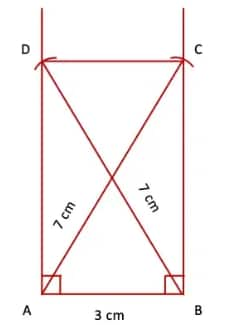
Q4. Construct a rectangle one of whose sides is 3 cm and the diagonal is of length 7 cm.
Answer:
Step 1. Draw a line segment AB = 3 cm. Draw perpendicular lines at points A and B.
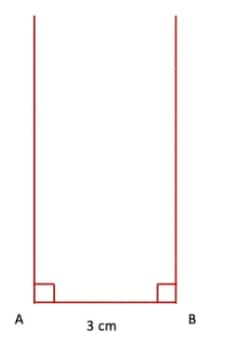
Step 2. With A as the centre and radius equal to 7 cm, draw an arc intersecting the perpendicular at B. Similarly, with B as the centre and radius equal to 7 cm, draw an arc intersecting the perpendicular at A.
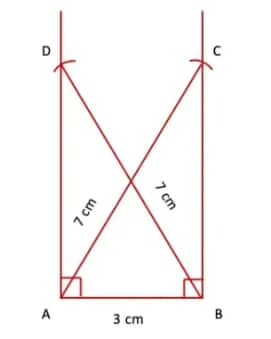
Step 3. (iii) Join points D and C.
ABCD is the required rectangle.
| Playing with Constructions Class 6 Question Answers Page number: 215 Number of Questions: 3 |
Construct
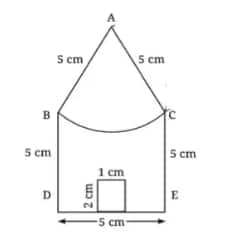
Q1. Construct a bigger house in which all the sides are of length 7 cm.
Answer:
Step 1. Draw a line segment DE = 7 cm. At points D and E, draw perpendicular lines.
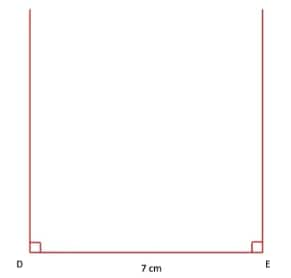
Step 2. Mark two points, B and C, on perpendiculars at points D and E such that DB = EC = 7 cm. With B and C as centres and a radius equal to 7 cm, draw arcs and let them intersect at point A. Join AB and AC.
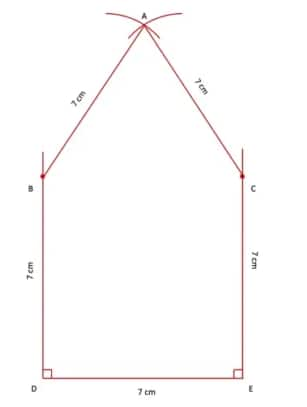
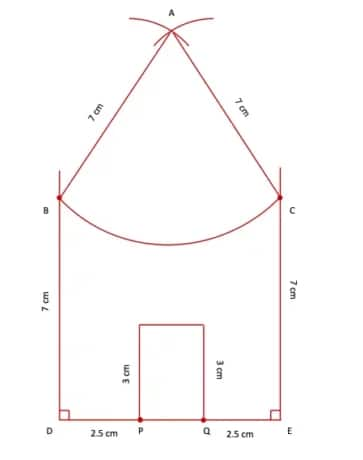
Step 3. With A as the centre and a radius equal to AB, draw an arc from point B to point C. Mark two points, P and Q, on DE such that DP = 2.5 cm and QE = 2.5 cm. Draw perpendicular lines at points P and Q, each of length 3 cm. Join the endpoints of both perpendiculars. The resultant figure is the required house.
Q2. Try to recreate ‘A Person’, ‘Wavy Wave’, and ‘Eyes’ from the section ‘Artworkʼ, using ideas involved in the ‘House’ construction.
Answer:
A Person
Wavy Wave

Eyes
Q3. Is there a 4-sided figure in which all the sides are equal in length but is not a square? If such a figure exists, can you construct it?
Answer:
Yes, a rhombus is a four-sided figure with all sides equal, but it is not a square.
A rhombus can be constructed by following the given steps:
(i) Draw a line segment AB = 6 cm. At point A, draw a ray ‘AX’ making an angle of 70° with AB. Similarly, at point B, draw a ray 'BY’ making an angle of 110° with AB.
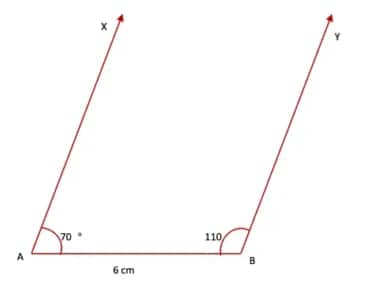
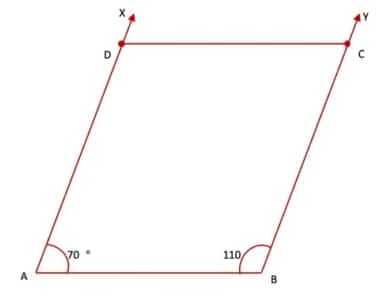
(ii) Mark a point D on ray AX such that AD = 6 cm. Also, mark another point C on ray ‘BY’ such that BC = 6 cm. Join points D and C.
Hence, ABCD is the required rhombus with all four sides equal, but it is not a square.
NCERT Playing with Constructions Class 6 Maths Chapter 8: Topics
Students will explore the following topics in the NCERT Class 6 Maths Chapter 8 Playing with Constructions:
8.1 Artwork
8.2 Squares and Rectangles
8.3 Constructing Squares and Rectangles
8.4 An Exploration in Rectangles
8.5 Exploring Diagonals of Rectangles and Squares
8.6 Points Equidistant from Two Given Points
Class 6 Maths Chapter 8 Playing with Constructions solutions: Extra Question
Question:
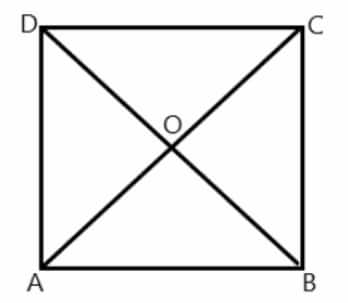
In a square, how do the diagonals behave? Draw a square and its diagonals, then explain how the diagonals are related to each other.
Answer:
In a square, both diagonals have the following properties:
-
They are equal in length.
-
They bisect each other, meaning they divide each other into two equal parts.
-
They intersect at right angles, i.e., they meet at a 90-degree angle.
NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Notes
Careers360 has prepared these Class 6 Playing with Constructions Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Playing with Constructions NCERT solutions and solve them independently from next time.
Important tools that are used in this chapter are:
Compass: It is a drawing instrument used for drawing circles or arcs.
Ruler: It is used for measuring and drawing straight lines.
Protractor: It is a measuring instrument, usually semicircular, used to measure and draw angles
How to construct a circle?
Imagine a point “x” on your notebook and adjust your compass as needed. If you need a bigger circle, then take a bigger length; if you need a smaller circle, take a smaller length.
Place the pointed end of the compass at the centre of the circle. Rotate the compass around to draw a full circle.
Draw a line from the centre of the circle to any point on the border of the circle using a ruler. This line is called the radius of the circle.
Some tips about the compass:
- Use sharp pencils for an accurate circle.
- Make sure the compass legs are not too tight or too loose.
Drawing a rectangle:
A rectangle has four sides, and the opposite sides are equal.
Use the ruler to draw the longest side of the rectangle. It is called the length of the rectangle.
From the endpoint of the first line, draw a straight line smaller than the first line. It is called the width of the rectangle.
From the other endpoint of the length, draw the same parallel line.
Now connect the endpoints of two parallel lines.
All the angles of the rectangle are right angles, i.e., 90 degrees.
Always use the protractor to measure exactly 90 degrees between adjacent sides.
Diagonals:
A rectangle has two diagonals, which are equal in length but not necessarily perpendicular.
If we connect the opposite corners of the rectangle, we will get the diagonal. Both diagonals will intersect at the midpoint of the rectangle.
Drawing a square:
A square is a special type of rectangle where all sides are of equal length.
Draw a straight line using the ruler of any length.
Then, from one endpoint of the length, draw another line of the same length. Do the same process from the other endpoint and connect the lines.
All the angles of the square are also right angles, i.e., 90 degrees
Always use the protractor to measure exactly 90 degrees between adjacent sides.
Diagonals:
A square also has two diagonals, and both diagonals are perpendicular.
They bisect each other at right angles and are also equal in length.
If we connect the opposite corners of the square, we will get the diagonal.
NCERT Solutions for Class 6 Maths Chapter 8 Playing with Constructions: Points to Remember
Check the following important points to understand and deal with Class 6 Maths Chapter 8 Playing with Constructions question answers effectively.
- Basic Geometrical Tools:
A ruler (Scale) is used for measuring lengths.
A compass is used for drawing circles and arcs.
A Protractor is used for measuring angles.
Setsquares are used for drawing perpendicular and parallel lines. - Drawing a Line Segment:
By using a ruler, we can draw a line segment of a given length.
Example: To draw a line segment 5 cm, mark points at 0 cm and 5 cm, then join these points. - Drawing a Circle:
We can use a compass with a fixed radius and then place the compass point at the centre and draw a circle. - Perpendicular Bisector of a Line Segment
First, use a compass to draw arcs above and below the line segment from both endpoints of the line segment, then we can draw a line through the intersection points of the arcs and get the perpendicular bisector of the line segment. - Perpendicular from a Point
Point on the line: Use a compass to draw arcs and then perpendicular lines.
Point outside the line: Draw arcs and connect to form a perpendicular line. - Angle Bisector
Draw arcs from the vertex of the angle.
Draw two intersecting arcs inside the angle.
Connect the vertex to this intersection point to get the bisector.
Why are Class 6 Maths Chapter 8 Playing with Constructions question answers important?
Playing with Constructions is an important chapter in class 6, as in this chapter, students will connect with geometry by drawing several geometrical figures using a ruler, a compass, and a protractor. Here are some more points on why the Class 6 Maths Playing with Constructions question answers are important.
- This chapter builds a strong base in identifying properties like sides, angles, and symmetry of quadrilaterals.
- These question answers introduce students to the concept of perpendicular bisectors and basic locus, useful in higher geometry.
- Also, practising questions from this chapter helps understand the properties of diagonals, symmetry, and congruency.
- Questions from this chapter often appear on several board exams and math Olympiads.
NCERT Solutions for Class 6 Mathematics Chapter-wise
We at Careers360 compiled all the NCERT class 6 Maths solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and NCERT Syllabus
Students can also check the NCERT Books and the NCERT Syllabus for Class 6 here:
Frequently Asked Questions (FAQs)
First, place the centre of the protractor on the vertex, align one side with the base line, and mark the required degree measure to draw the other side.
A triangle can be constructed when any of the following are known:
Three sides
Two sides and an included angle
Two angles and the included side
Because even small errors can make figures incorrect. Accuracy ensures that angles, sides, and shapes are drawn correctly.
Yes, many educational platforms, such as Careers360, offer free downloadable PDFs of NCERT Playing with Constructions Class 6 Chapter 8 Question Answers. Students can find the free downloadable PDF in this article itself.
Squares and rectangles are fundamental shapes used in drawings, designs, and architecture; understanding their properties helps ensure accurate construction.
Instruments like a compass, ruler, protractor, and divider are mainly used for constructions in this chapter.
Yes, these solutions give clear steps with diagrams to guide the construction process.
This chapter focuses on using geometric instruments to construct basic figures, such as angles, bisectors, and simple shapes, with accuracy.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
