NCERT Solutions for Class 6 Maths Chapter 6 - Perimeter and Area

Perimeter and area are one of the fundamental concepts in mathematics that help students understand the way to calculate the length of the boundary and the area enclosed within the boundary. Perimeter refers to the length of the boundary, while area refers to the surface area enclosed within the boundary. These perimeter and area play a major role in many real-life situations, like calculating the amount of paint required to paint a wall and the length of the fence required, etc. This articles consist of the solutions for all the questions in this chapter. NCERT Solutions Class 6 Maths Chapter 6 Perimeters and Areas will help you to understand all the concepts related to it.

Latest: Important Maths Formulas for Class 6 - Chapterwise

This Story also Contains

1. NCERT Solutions for Class 6 Maths Chapter 6 Exercise
2. Perimeter and Area Class 6 Maths Chapter 6-Topics
3. NCERT Solutions for Class 6 Maths Chapter 6 Perimeter and Area - Notes
4. NCERT Solutions for Class 6 Maths Chapter 6 Perimeter and Area - Points to Remember
5. NCERT Solutions for Class 6 Maths Chapter Wise
6. NCERT Solutions for Class 6 Subject Wise

These solutions provide comprehensive step-by-step solutions for all the questions in this chapter. These reliable NCERT Solutions for Class 6 Maths can be used by the students for exam preparation as they are created by the subject matter experts of Careers360. Students can refer to the NCERT Solutions for Class 6 to access the subject-wise solutions of Class 6.

NCERT Solutions for Class 6 Maths Chapter 6 Exercise

Page no: 132

1. Find the missing terms:

a. Perimeter of a rectangle $=14\mathrm{cm}$; breadth $=2\mathrm{cm}$; length $=$ ?

b. Perimeter of a square $=20\mathrm{cm}$; side of a length $=$ ?

c. Perimeter of a rectangle $=12\mathrm{m}$; length $=3\mathrm{m}$; breadth $=$ ?

Solution:

a. Given: Perimeter of a rectangle $=14\mathrm{cm}$, breadth $=2\mathrm{cm}$ Perimeter of Rectangle = $2\times (L+B)$, where $L$ is the length and $B$ is the breadth of the rectangle.

$\Rightarrow 14=2\times (L+2)$

$\Rightarrow 7=L+2$

$\Rightarrow L=5$ cm

b. Given: Perimeter of a Square $=20\mathrm{cm}$

Perimeter of square $=4\times (side)$

$20=4\times (sides)$

$\Rightarrow \Rightarrow \frac{20}{4}=side$

$\Rightarrow side=5$ cm

c. Given: Perimeter of a rectangle $=12\mathrm{m}$; length $=3\mathrm{m}$

The perimeter of a rectangle is $P=2(l+b)$, where $l$ is the length and $b$ is the breadth of the rectangle.

$\Rightarrow 12=2(3+b)$

$\Rightarrow 6=3+b$

$\Rightarrow b=6-3=3$ cm

2. A rectangle having sidelengths 5 cm and 3 cm is made using a piece of wire. If the wire is straightened and then bent to form a square, what will be the length of a side of the square?

Solution:
Perimeter of the rectangle $=2\times (l+b)$, where $l$ is the length and $b$ is the breadth of the rectangle.

Here perimeter of the rectangle $=2(5+3)$

$=2\times 8$

$=16\mathrm{cm}$

Now the wire is straightened and then bent to form a square.

Perimeter of Square $=4\times a$, where $a$ is the side of the square.

$\therefore$ Perimeter of square $=16\mathrm{cm}$

$\Rightarrow 4a=16\mathrm{cm}$

$\Rightarrow a=4\mathrm{cm}$, the required length of the side of the square.

3. Find the length of the third side of a triangle having a perimeter of 55 cm and having two sides of length 20 cm and 14 cm, respectively.

Solution:
Perimeter of Triangle $=$ Sum of all three sides of the triangle

First side of the triangle $=20\mathrm{cm}$

Second side of the triangle $=14\mathrm{cm}$

Let the third side of the triangle be ' $x$ '

Perimeter of the triangle $=55\mathrm{cm}$

$\therefore 20+14+x=55cm$

$\Rightarrow 34+x=55cm$

$\Rightarrow x=55-34$

$\Rightarrow x=21$

$\therefore$ the length of the third side of the triangle is 21 cm.

4. What would be the cost of fencing a rectangular park whose length is 150 m and breadth is 120 m, if the fence costs ₹ 40 per metre?

Solution:
Perimeter of the rectangle $=2(l+b)$ [Where ‘l’ is the length of the Park and ‘b’ is the breadth of the Park]

The length of the fence is the perimeter of the rectangular park.

Given that the length of the rectangular park $=150\mathrm{m}$ and breadth $=120\mathrm{m}$

$=2\times (150+120)$

$=2\times (270)$

$=540m$

Now the cost of fencing per meter $=Rs.40$

The cost of fencing the rectangular park is $=Rs.40\times 540=Rs.21600$

5. A piece of string is 36 cm long. What will be the length of each side, if it is used to form:

a. A square

b. A triangle with all sides of equal length, and

c. A hexagon (a six-sided closed figure) with sides of equal length?

Solution:
Given: A piece of string is 36 cm long

a. Given that a piece of string is 36 cm long

$\therefore$ length of each side of the square $=a$,

Perimeter of a Square $=4\times a$

Perimeter $=36$
$\Rightarrow 4a=36$
$\Rightarrow a=\frac{36}{4}$
$\Rightarrow a=9$ cm

b. Length of each side of the triangle $=a$ (Given)

Perimeter of a triangle $=$ Sum of all sides of a Triangle

Perimeter $=36$
$\Rightarrow 3a=36$
$\Rightarrow a=\frac{36}{3}$
$\Rightarrow a=12$ cm

c. Length of each side of hexagon $=x$

Perimeter of Hexagon $=$ Sum of all sides of a hexagon

Perimeter $=36$
$\Rightarrow 3a=36$
$\Rightarrow a=\frac{36}{3}$
$\Rightarrow a=12$ cm

6. A farmer has a rectangular field with a length of 230 m and a breadth of 160 m. He wants to fence it with 3 rounds of rope as shown. What is the total length of rope needed?

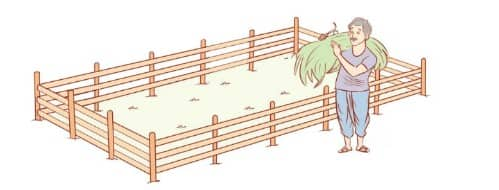
Solution: Perimeter of the rectangular field $=2(l+b)$

Given $\mathrm{l}=230\mathrm{m},\mathrm{b}=160\mathrm{m}$
$\therefore P=2\times (230+160)$
$=2\times 390$
$=780$ m

Distance covered in one round $=780\mathrm{m}$

$\therefore$ Required length of rope $=3\times 780=2340\mathrm{m}$

Page no: 133

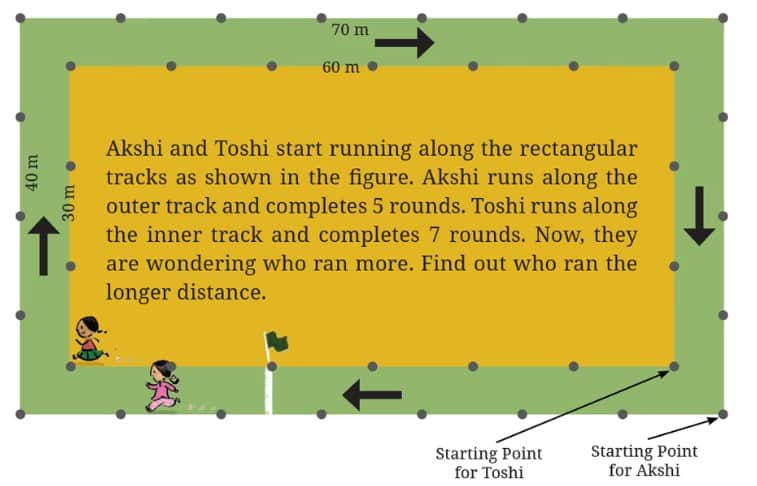
Each track is a rectangle. Akshi's track has a length of 70 m and a breadth of 40 m. Running one complete round on this track would cover 220 m, i.e., $2\times (70+40)\mathrm{m}=220\mathrm{m}$. This is the distance covered by Akshi in one round.

1. Find out the total distance Akshi has covered in 5 rounds.

Solution:
Distance covered by Akshi in 5 rounds $=5\times$ perimeter of outer rectangle

$=5\times 220$

$=1100$ m

2. Find out the total distance Toshi has covered in 7 rounds. Who ran a longer distance?

Solution :
Distance covered by Toshi in 7 rounds $=7\times 180=1260\mathrm{m}$ $\therefore 1260\mathrm{m}>1100\mathrm{m}$

Hence, Toshi ran the longer distance.

3. Think and mark the positions as directed-

a. Mark 'A' at the point where Akshi will be after she has run 250 m.

b. Mark 'B' at the point where Akshi will be after she has run 500 m.

c. Now, Akshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as 'C'.

d. Mark ' $X$ ' at the point where Toshi will be after she has run 250 m.

e. Mark ' Y ' at the point where Toshi will be after she has run 500 m.

f. Now, Toshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ' $Z$ '.

Solution:

a. Here, one round of a rectangular field is $=220$ meters.

The distance Akshi has run is $=250$ meters.

Extra distance beyond one round $=250-220=30$ meters.

Since Akshi has already completed one full round, she will be 30 meters into her second round.

Thus, after running an additional 30 meters, she will be on the length side of the track, 30 meters from the starting point. Therefore, mark 'A' at the point 30 meters along the length of the track from the starting point.

b. Distance per round $=220$ meters

Total distance Akshi runs = $500$ meters.

First, we will find out how many complete rounds she runs:

Number of complete rounds $=\frac{500}{220}=2.27$ (approx)

This means Akshi completes 2 full rounds and then runs an additional distance $=500-(2\times 220)=60\mathrm{m}$ Therefore, Akshi will be 60 meters along the length of the track from the starting point, we can mark point ' B ' at this position on the track.

c. Now, Akshi ran 1000 meters.

Number of full rounds $=\frac{1000}{220}=4.545$ rounds.

Akshi has completed 4 full rounds and is partway through her 5th round.

To find her position on the track, we calculate the remaining distance after 4 full rounds:

Remaining distance $=1000\mathrm{m}-(4\times 220\mathrm{m})$

$=1000-880$

$=120$ m

Since she has run an additional 120 meters after completing 4 full rounds, her position will be 120 meters from the starting point. If we mark her starting point as 'P', her position after running 1000 meters can be marked as ' $C$ ', which is 120 meters from ' $A$ ' along the track.

d. Perimeter of the track $=180$ meters

Distance Toshi runs $=250$ meters

Since 250 meters is more than one complete round ( 180 meters), Toshi will have completed one full round and will have 70 meters left to run ( $250-180=70$ meters). So, Toshi will be 70 meters along the length of the track from the starting point. You can mark ' $X$ ' at this point on the track.

e. Given that Toshi has run an additional 140 meters after completing 2 rounds, her position will be 140 meters from the starting point. If we mark her starting point as ' A ', her position after running 500 meters can be marked as ' $Y$ '.

f. Number of full rounds $=\frac{1000}{180}=5.56$

Toshi has finished 5 full rounds.

Remaining distance $=1000$ meters $-(5\times 180$ meters $)$

$=1000$ meters $-900$ meters

$=100$ meters

Starting from the initial point, Toshi would be 100 meters into her 6th round. Since the track is 60 meters long and 30 meters wide, she would be somewhere along the length of the track.

Let's mark this position as ' $Z$ '.

Page no: 138

1. The area of a rectangular garden 25 m long is 300 sq m. What is the width of the garden?

Solution:
Given, area of rectangular garden $=300$ sq.m and length $=25\mathrm{m}$

area of rectangular field $=\mathrm{l}\times \mathrm{b}$
$\Rightarrow 300=25\times b$
$\Rightarrow b=\frac{300}{25}$ m
$\Rightarrow b=12$ m

2. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of $Rs.8$ per hundred sq m?

Solution: Length $=500\mathrm{m}$ and breadth $=200\mathrm{m}$

Hence the area of the rectangular plot $=$ length $\times$ breadth
$=500\times 200$
$=1,00,000$ m²

Now the cost of tilling a rectangular plot is Rs. $\frac{8}{100}$ per sq. m

Hence, the cost of tilling 1,00,000 sq. m of rectangular plot $=\frac{8}{100}\times 100000=$ Rs. 8,000

3. A rectangular coconut grove is 100 m long and 50 m wide. If each coconut tree requires 25 sq m, what is the maximum number of trees that can be planted in this grove?

Solution: Area of rectangular coconut grove $=100\times 50=5000$ sq. m

Given each coconut tree requires 25 sq. m, then the maximum no. of trees that can be planted in this grove is $=\frac{5000}{25}=200$

4. By splitting the following figures into rectangles, find their areas (all measures are given in metres).

a.

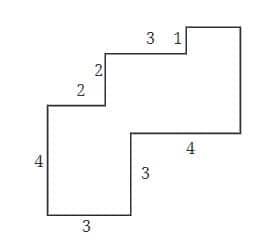
Solution:
a.

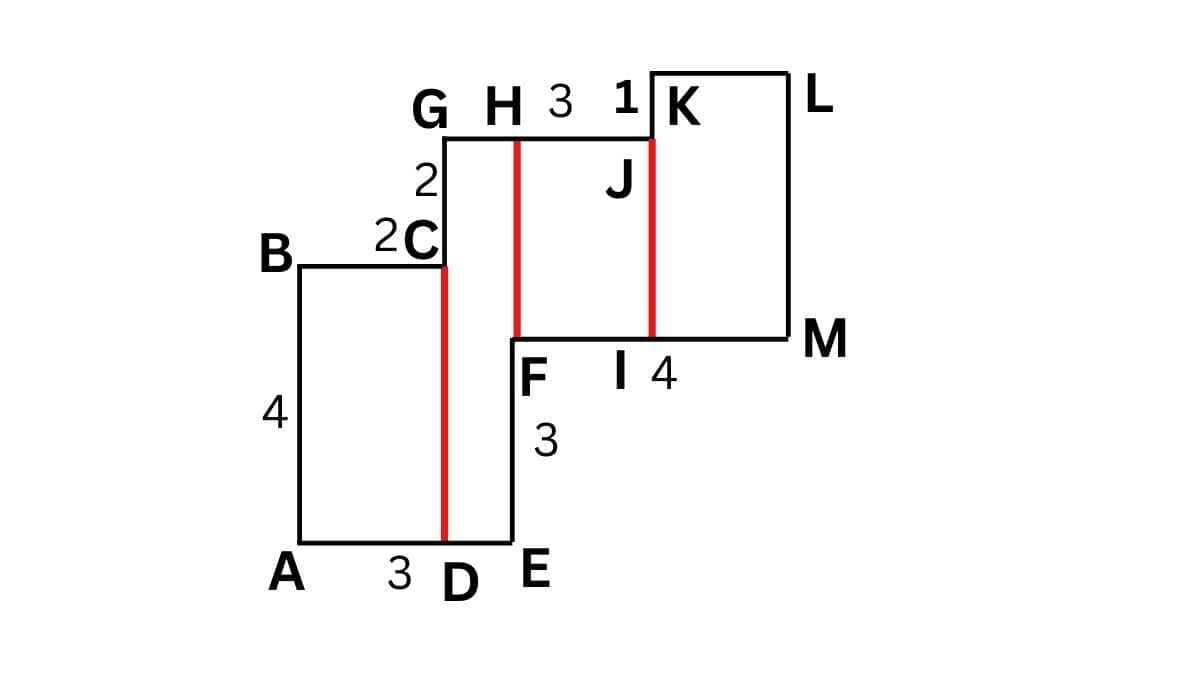
There will be four rectangles as shown in the figure.
Total Area = Area of rectangle ABCD + Area of rectangle DGHE + Area of rectangle FHKI + Area of rectangle KLMI
= $AB\times BC+DG\times DE+HF\times JH+LM\times KL$
= $4\times 2+(4+2)\times (3-2)+(4+2-3)\times (3-1)+(3+1)\times (1+4-3)$
= $8+6+6+8$
= 28 m²

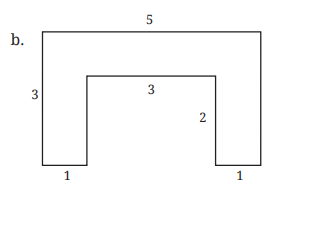
b.

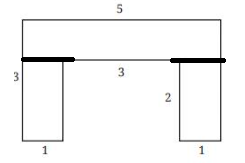
There are three rectangles as shown in the figure
So, the required area = Area of the sum of three triangles
= $5\times 1+2\times 1+2\times 1$
= $5+2+2$
= $9$ m²

Page no: 139

Cut out the tangram pieces given at the end of your textbook.

1. Explore and figure out how many pieces have the same area.

Solution:
Shapes C and E are the two pieces with the same area. Similarly, A and B also have the same area.

2. How many times bigger is Shape D as compared to Shape C? What is the relationship between Shapes C, D, and E?

Solution:
As you can see in the figure, shape $D$ is twice the size of Shape C.

The area of Shape D is equal to the sum of the areas of Shape C and Shape E.

$\Rightarrow$ Shape C + Shape E = Shape D.

3. Which shape has more area: Shape D or F? Give reasons for your answer.

Solution:
Both Shape D and Shape $F$ have equal area.

It's because Shape C and Shape E together fit perfectly into both Shape D and Shape F.

4. Which shape has more area: Shape F or G? Give reasons for your answer.

Solution:
Both Shape F and Shape G have equal area.

It's because Shape C and Shape E together fit perfectly into both Shape F and Shape G.

5. What is the area of Shape A as compared to Shape G? Is it twice as big? Four times as big?

(Hint: In the tangram pieces, by placing the shapes over each other, we can find out that Shapes A and B have the same area, Shapes C and E have the same area. You would have also figured out that Shape D can be exactly covered using Shapes C and E, which means Shape D has twice the area of Shape C or Shape E, etc.)

Solution:
The area of Shape A is twice as big as Shape G.

6. Can you now figure out the area of the big square formed with all seven pieces in terms of the area of Shape C?

Solution:
The area of the big square is 16 times the area of Shape C.

7. Arrange these 7 pieces to form a rectangle. What will be the area of this rectangle in terms of the area of Shape C now? Give reasons for your answer.

Solution:
The area of the rectangle formed by combining all 7 pieces will be 16 times the area of Shape C. This is because the total area of all the pieces will remain the same, regardless of how they are aligned.

8. Are the perimeters of the square and the rectangle formed from these 7 pieces different or the same? Explain your answer.

Solution:
The perimeter of the square and the rectangle formed from these 7 pieces will be different. This is because the distance around the outside of the shape is different.

Page no: 144

1. Find the areas of the figures below by dividing them into rectangles and triangles.

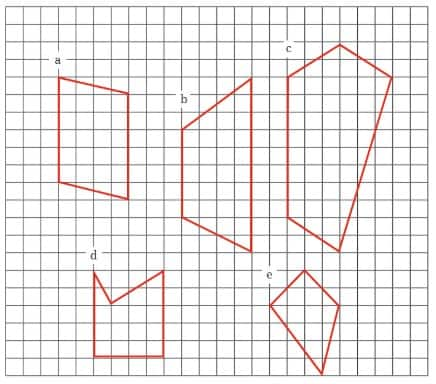
Solution:

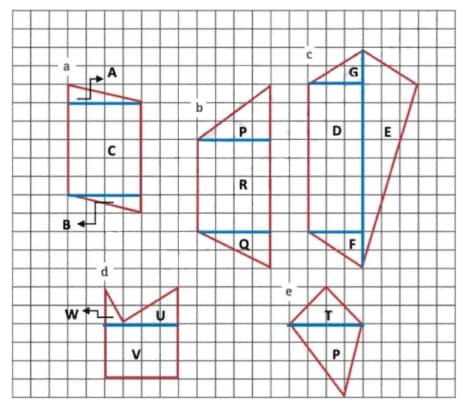
(a) Area of the figure $=$ Area of triangle $A+$ Area of triangle $B+$ Area of rectangle $C$
$=\frac{1}{2}\times$ Base $\times$ Height + $\frac{1}{2}\times$ Base $\times$ Height + Length $\times$ Breadth
$=(2+20+2)$ sq. units
$=24$ sq. units.

(b) Area of the figure $=$ Area of triangle $\mathrm{P}+$ Area of triangle $\mathrm{Q}+$ Area of rectangle $R$

$=\frac{1}{2}\times$ Base $\times$ Height + $\frac{1}{2}\times$ Base $\times$ Height + Length $\times$ Breadth
$=6$ sq. units +4 sq. units +20 sq. units
$=30$ sq. units.

(c) Area $=$ Area of triangle G + Area of triangle E + Area of triangle F + Area of rect. D
$=\frac{1}{2}\times$ Base $\times$ Height + $\frac{1}{2}\times$ Base $\times$ Height + Length $\times$ Breadth
$=3$ sq. units +18 sq. units +3 sq. units +24 sq. units
$=48$ sq. units.

(d) Area of the figure $=$ Area of triangle $\mathrm{W}+$ Area of triangle $\mathrm{U}+$ Area of rectangle $V$
$=\frac{1}{2}\times$ Base $\times$ Height + $\frac{1}{2}\times$ Base $\times$ Height + Length $\times$ Breadth
$=1$ sq. units +3 sq. units +12 sq. units
$=16$ sq. units.

(e) Area of the figure $=$ Area of triangle $T+$ Area of triangle $P$
$=\frac{1}{2}\times$ Base $\times$ Height + $\frac{1}{2}\times$ Base $\times$ Height
$=4$ sq. units +7 sq. units
$=11$ sq. units.

Page no: 149

1. Give the dimensions of a rectangle whose area is the sum of the areas of these two rectangles having measurements: $5\mathrm{m}\times 10\mathrm{m}$ and $2\mathrm{m}\times 7\mathrm{m}$.

Solution:
The sum of the areas of these two rectangles $=(5\times 10+2\times 7)\mathrm{sq}\mathrm{m}=64\mathrm{sq}\mathrm{m}$

Now, the rectangle has an area of $64m^2$

So, the dimensions of rectangle $=16\mathrm{m}\times 4\mathrm{m}$

2. The area of a rectangular garden that is 50 m long is 1000 sq m. Find the width of the garden.

Solution:
Length of a rectangular garden $=50\mathrm{m}$
Area of the rectangular garden $=1000$ sq m

Now,
$\therefore$ Area of the rectangular garden $=$ length $\times$ width
$\therefore 1000=50\times$ width
$\therefore$ Width $=\frac{1000}{50}=20$
So, the width of the rectangular garden $=20\mathrm{m}$

3. The floor of a room is 5 m long and 4 m wide. A square carpet whose sides are 3 m in length is laid on the floor. Find the area that is not carpeted.

Solution:
Length of a room $=5\mathrm{m}$
Width of the room $=4\mathrm{m}$

So, area of the room $=\text{Length of a room}\times \text{Width of the room}=5\times 4\mathrm{sq}\mathrm{m}=20\mathrm{sq}\mathrm{m}$

Now, the length of the sides of a square carpet is $=3\mathrm{m}$

Area of the carpet $={\text{(length of the sides of a square carpet)}}^2=3\times 3\mathrm{sq}\mathrm{m}=9\mathrm{sq}\mathrm{m}$

The area that is not carpeted is $=(20-9)\mathrm{sq}\mathrm{m}=11\mathrm{sq}\mathrm{m}$

4. Four flower beds, having sides 2 m long and 1 m wide, are dug at the four corners of a garden that is 15 m long and 12 m wide. How much area is now available for laying down a lawn?

Solution:
Length of garden = 15 m

Width of garden $=12\mathrm{m}$

So, the area of the garden $=\text{Length of Garden}\times \text{Width of Garden}=15\times 12\mathrm{sq}\mathrm{m}=180\mathrm{sq}\mathrm{m}$

Now, length of flower bed $=2\mathrm{m}$

Width of flower bed $=1\mathrm{m}$

Area of the flower bed $=\text{Length of flower bed}\times \text{Width of flower bed}=2\times 1\mathrm{sq}\mathrm{m}=2\mathrm{sq}\mathrm{m}$

Since, the area of four flower beds $=2\times 4\mathrm{sq}\mathrm{m}=8\mathrm{sq}\mathrm{m}$

Now the area is available for laying down a lawn $=(180-8)$ sq $\mathrm{m}=172\mathrm{sq}\mathrm{m}$

5. Shape A has an area of 18 square units, and Shape B has an area of 20 square units. Shape A has a longer perimeter than Shape B. Draw two such shapes satisfying the given conditions.

Solution:

Shape A

Area = $9\times 2=18$ square units
Perimeter = 9 + 9 + 2 + 2 = 22 units

Shape B

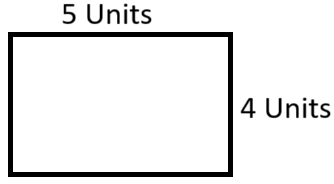
Area = $5\times 4=20$ square units
Perimeter = 5 + 5 + 4 + 4 = 20 units

Clearly, shape A has more perimeter than that of B.

6. On a page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides. What is the perimeter of the border?

Solution:
Let the width of the page $=W$ cm
Width of the border $=W-1.5\mathrm{cm}$ (left margin) $-1.5$ cm (right margin) $=\mathrm{W}-3\mathrm{cm}$.

Let the height of the page $=H$ cm
Height of the border $=\mathrm{H}-1\mathrm{cm}$ (top margin) $-1$ cm (bottom margin) $=\mathrm{H}-2\mathrm{cm}$.

Perimeter of the border $=2\times$(Width of the border + Height of the border)
$=2\times ((W-3)+(H-2))=2\times (W+H-5)$
$=2(W+H)-10$

The perimeter of the border is $2(W+H)-10$ cm.

7. Draw a rectangle of size 12 units $\times 8$ units. Draw another rectangle inside it, without touching the outer rectangle that occupies exactly half the area.

Solution: Area of rectangle $=12\times 8$ sq units $=96$ sq units

The area of the new rectangle is half of this rectangle, so the area of the new rectangle $=\frac{1}{2}\times 96sq\mathrm{m}=48\mathrm{sq}\mathrm{m}$

The possible dimensions of new rectangle $=8$ units $\times 6$ units

8. A square piece of paper is folded in half. The square is then cut into two rectangles along the fold. Regardless of the size of the square, one of the following statements is always true. Which statement is true here?

a. The area of each rectangle is larger than the area of the square.

b. The perimeter of the square is greater than the perimeter of both the rectangles added together.

c. The perimeters of both the rectangles added together are always $1\frac{1}{2}$ times the perimeter of the square.

d. The area of the square is always three times as large as the areas of both rectangles added together.

Solution:

(a) False because the area of each rectangle is exactly half of the area of the square.

(b) False because the perimeter of the two resulting rectangles combined is greater than the perimeter of the square, as now we have two extra edges.

(c) True.
Let the side of the square be $x$ units.
After cutting it into two equal parts, the dimensions of each rectangle will be $x$ and $\frac{x}{2}$ units.
Perimeter of square = 4$x$
Perimeter of each rectangle = $2\times (x+\frac{x}{2})=3x$
Sum of the perimeter of two rectangles = $6x=\frac{3}{2}\times 4x$
Clearly, Sum of the perimeter of two rectangles = $1\frac{1}{2}\times$ perimeter of square

(d) False because the area of the square is equal to the sum of the areas of both the rectangles combined.

Perimeter and Area Class 6 Maths Chapter 6-Topics

• Perimeter
• Area

NCERT Solutions for Class 6 Maths Chapter 6 Perimeter and Area - Notes

Perimeter and Area: Perimeter is defined as the boundary that is covered by a 2-dimensional shape, while Area is the space enclosed within the boundary of the specific shape.

In class fifth, we have learned about the perimeter and area of some simple shapes like rectangles and squares. In class sixth, we will take our journey further and enhance our conceptual knowledge regarding the perimeter and area of triangles and other polygons that we commonly come across in geometry.

Perimeter and Area of Different Shapes

Rectangle

A rectangle is defined as a two-dimensional shape that has two pairs of equal and opposite sides.

Perimeter of a rectangle: The perimeter of a rectangle is given by P = 2(length + breadth)

Area of a rectangle: The area of a rectangle is given by the formula, length $\times$ breadth (i.e,) $l\times b$.

Square

A square is a two-dimensional figure that has all its sides equal in measurement. All the angles of a square are equal to 90 degrees.

Perimeter of a Square: The perimeter of a square is given by P = 4 $\times$ side (i.e,) $4\times s$

Area of a square: The area of a square is given by the formula, side $\times$ side (i.e,) $s\times s$.

Triangle

A triangle is a three-sided polygon.

Perimeter of a triangle: The perimeter of a triangle is given by P = the sum of all three sides. (i.e.) P = a+b+c

Regular Polygon

Like squares, closed figures that have all sides and all angles equal are called regular polygons. A few examples of regular polygons are the equilateral triangle (where all three sides and all three angles are equal), regular pentagon (where all five sides and all five angles are equal).

Perimeter of a regular polygon: The perimeter of a regular polygon is given by P = number of sides $\times$ length of sides

For example, the perimeter of an equilateral triangle = 3 $\times$ the length of a side.

NCERT Solutions for Class 6 Maths Chapter 6 Perimeter and Area - Points to Remember

Perimeter:

Perimeter of a square: P = 4 $\times$ side
Perimeter of a rectangle: P = length $\times$ breadth
Perimeter of a triangle: P = sum of all three sides
Perimeter of a regular polygon: P = number of sides $\times$ length of the side

Area:

Area of a square: A = side $\times$ side
Area of a rectangle: A = length $\times$ breadth

NCERT Solutions for Class 6 Maths Chapter Wise

NCERT Solutions for Class 6 Subject Wise

It is very important for the students to practice the exercise questions during the exam preparation. So, the students can refer to the subject-wise solutions prepared by the subject matter experts at Careers360 using the link below.

• NCERT Solutions for Class 6 Maths
• NCERT Solutions for Class 6 Science

Students can also check the NCERT Books and the NCERT Syllabus here:

• NCERT Syllabus Class 6 Maths
• NCERT Books Class 6
• NCERT Syllabus Class 6