NCERT Solutions for Class 6 Maths Chapter 9 - Symmetry
In the world of mathematics, symmetry is the art of balance and beauty hidden in shapes. Symmetry helps us create neat and accurate figures. We find many objects around us in various forms. The sun, nature, stars, moon, birds, and humans are all a part of this beautiful universe. We, as humans, tend to analyse these objects with our eyes and find similar patterns in them. We observe that certain patterns are repeated in some figures, such as flowers and bees. This is known as symmetry. In NCERT Class 6 Chapter 9 Symmetry, students will learn about all these topics. These NCERT Solutions are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Download Free PDF
- NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Exercise Questions
- NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Notes
- NCERT Symmetry Class 6 Maths Chapter 9: Topics
- Class 6 Maths Chapter 9 Symmetry solutions: Extra Question
- NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Points to Remember
- Why are Class 6 Maths Chapter 9 Symmetry question answers important?
- NCERT Solutions for Class 6 Maths Chapter Wise
- NCERT Books and Syllabus
Symmetry helps us understand patterns in nature. These NCERT solutions help students understand this concept in a better and practical way. These NCERT Solutions for Class 6 Maths are a crucial study resource that helps students understand various topics, including symmetry, lines of symmetry, rotational symmetry, and reflection. Students can refer to the NCERT Solutions for Class 6 to practice more problems during exam preparation. For detailed solutions, complete syllabus notes, and a free PDF download, refer to this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Download Free PDF
Careers360 brings you NCERT Solutions for Class 6 Maths Chapter 9 Symmetry, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Exercise Questions
Below are the detailed Class 6 Maths Chapter 9 Symmetry question answers provided in the textbook.
| Symmetry Class 6 Question Answers Page number: 219 Number of Questions: 2 |
Question 1: Do you see any line of symmetry in the figures at the start of the chapter? What about in the picture of the cloud?

Solution:
There is a line of symmetry in a flower, a butterfly, and a rangoli.
This flower has 6 lines of symmetry.
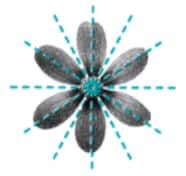
Butterfly has 1 line of symmetry.

This rangoli has 4 lines of symmetry.
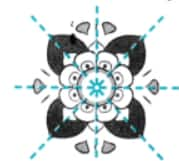
But no line of symmetry can be found in the clouds or the pinwheel.
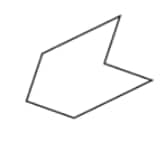
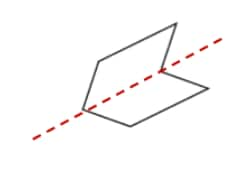
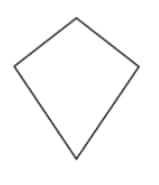
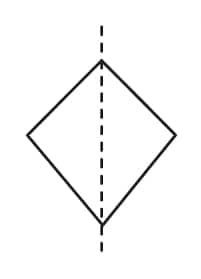
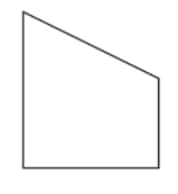
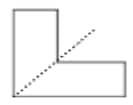
Question 2: For each of the following figures, identify the line(s) of symmetry if they exist.
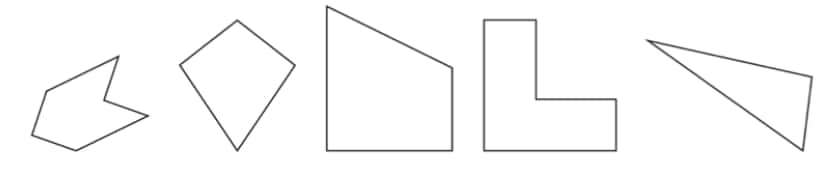
Solution:
|
Shapes |
Number of lines of symmetry |
Graphical design |
|
|
1 line of symmetry. |
|
|
|
1 line of symmetry. |
|
|
|
No lines of symmetry. | |
|
|
1 line of symmetry. |
|
|
|
No lines of symmetry. |
|
Symmetry Class 6 Question Answers |
Punching Game: The fold is a line of symmetry. Punch holes at different locations of a folded square sheet of paper using a punching machine and create different symmetric patterns.
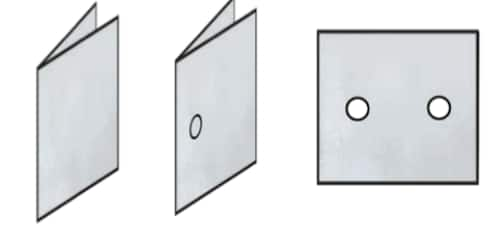
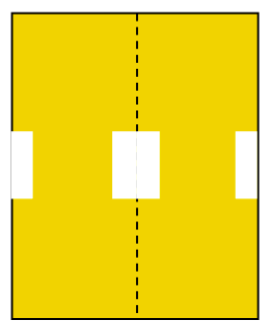
Question 1: In each of the following figures, a hole was punched in a folded square sheet of paper, and then the paper was unfolded. Identify the line along which the paper was folded. Figure (d) was created by punching a single hole. How was the paper folded?
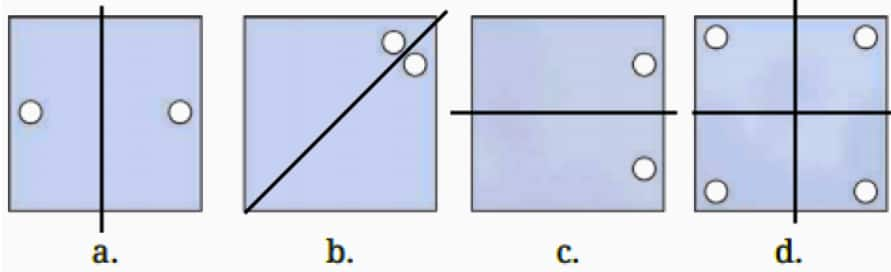
Solution:
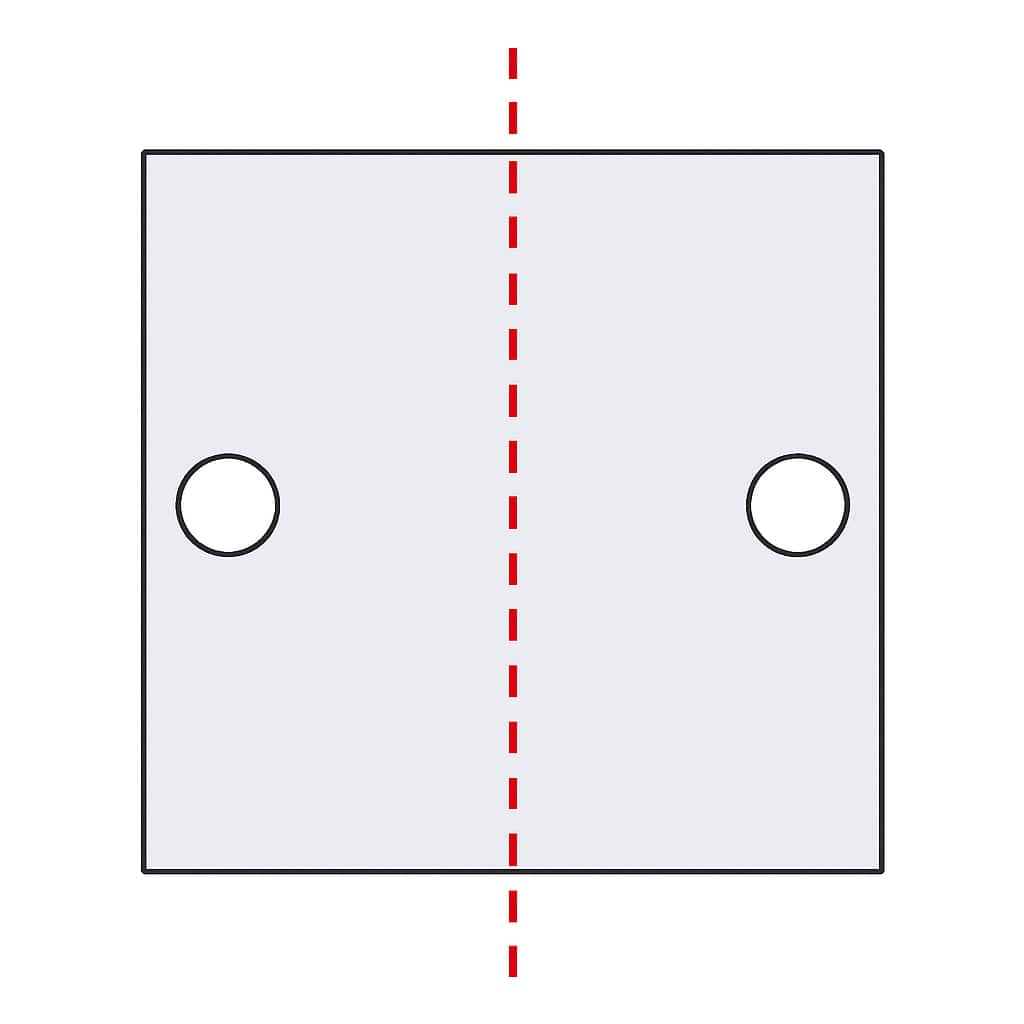
a.
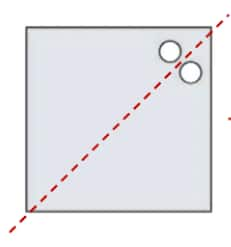
b.
c.

d.
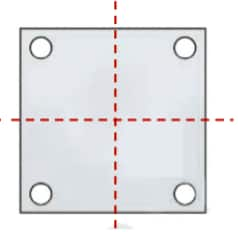
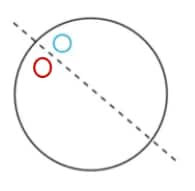
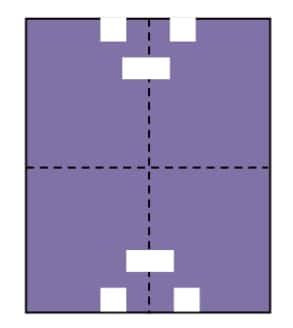
Question 2: Given the line(s) of symmetry, find the other hole(s):
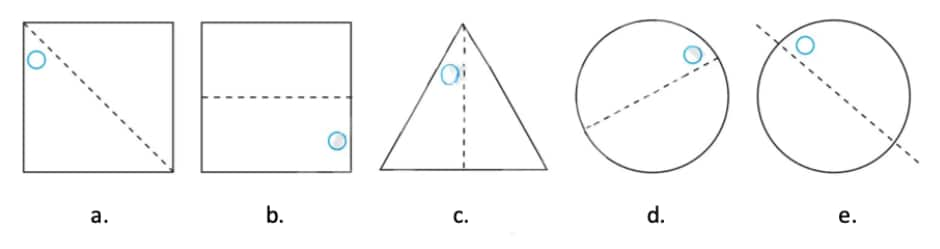
Solution:
a.
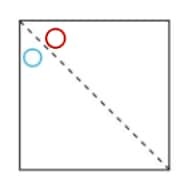
b.
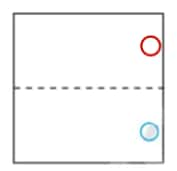
c.
d.
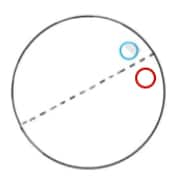
e.
Question 3: Here are some questions on paper cutting. Consider a vertical fold. We represent it this way:

Similarly, a horizontal fold is represented as follows:

Solution:
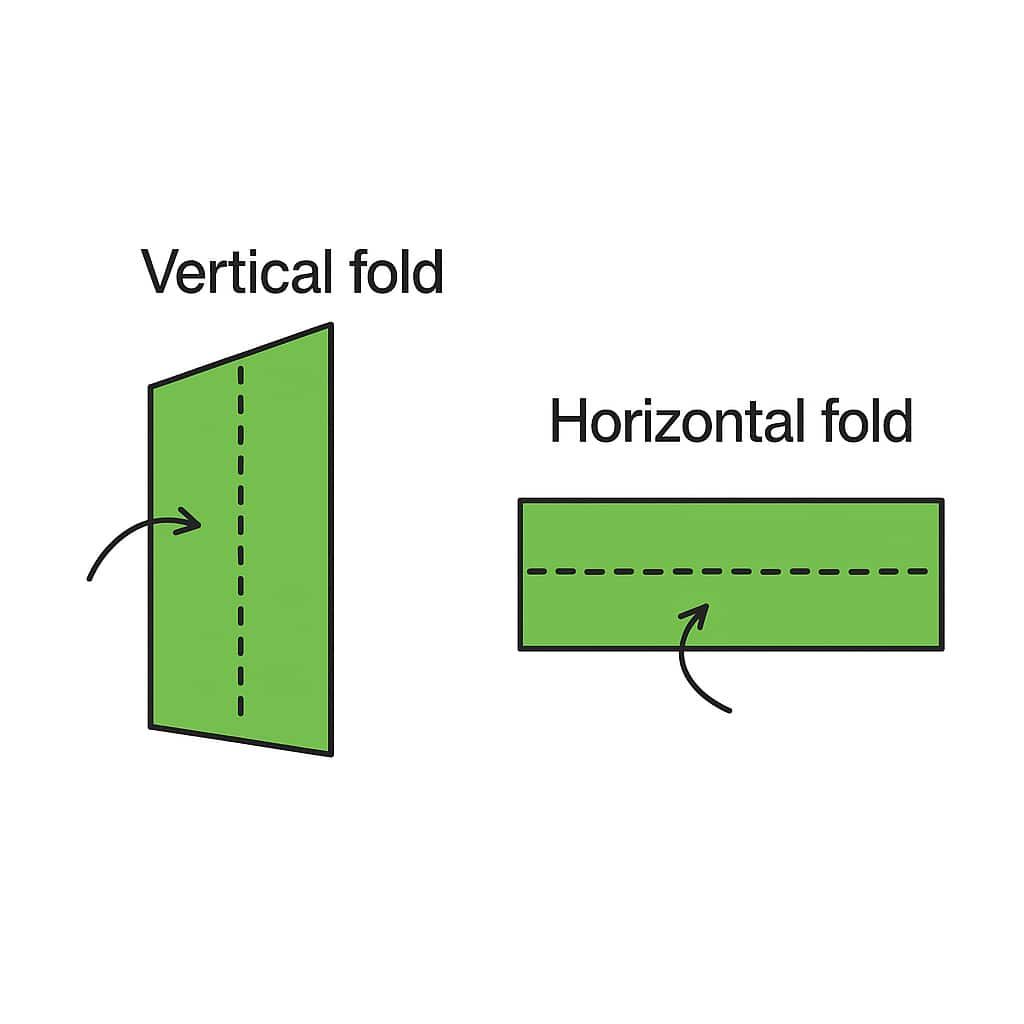
Question 4: After each of the following cuts, predict the shape of the hole when the paper is opened. After you have made your prediction, make the cutouts and verify your answer.
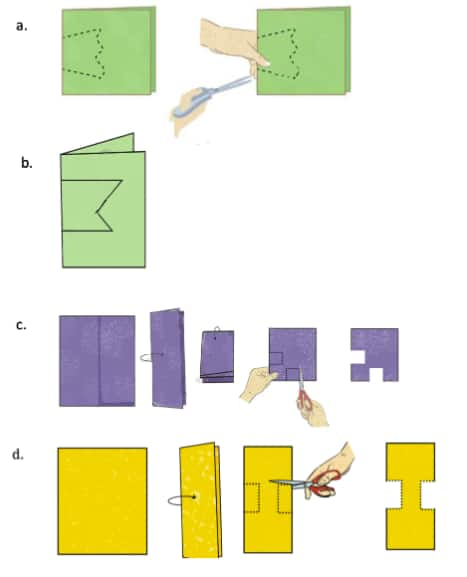
Solution:
a.
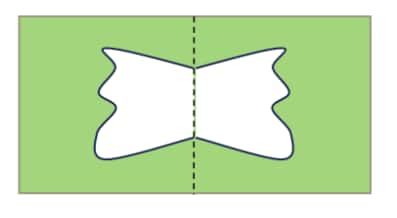
b.
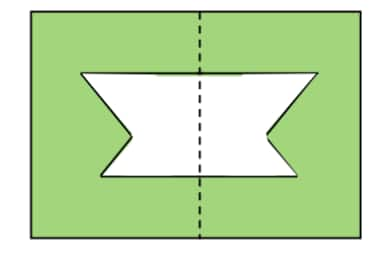
c.
d.
Question 5: Suppose you have to get each of these shapes with some folds and a single straight cut. How will you do it?
a. The hole in the centre is a square.

b. The hole in the centre is a square.

Note: For the above two questions, check if the 4-sided figures in the centre satisfy both the properties of a square.
Solution:
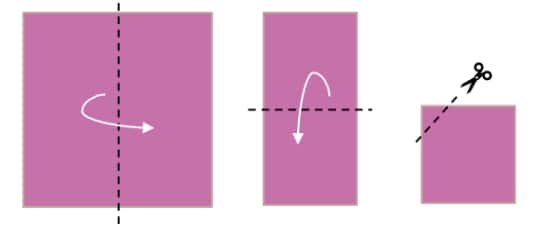
a.
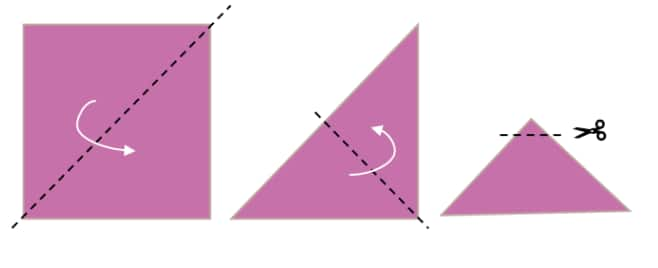
b.
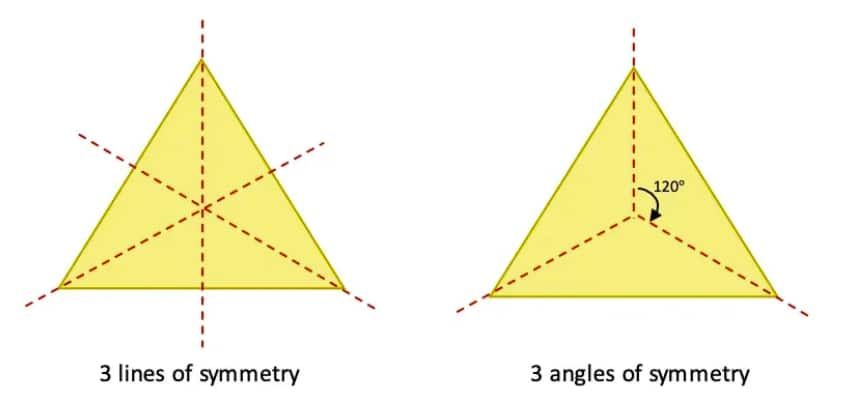
Question 6: How many lines of symmetry do these shapes have?
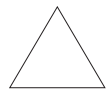
a. 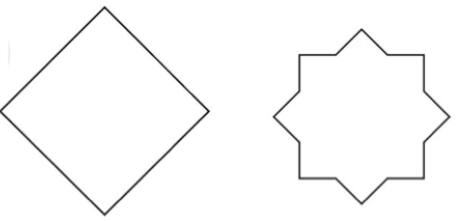
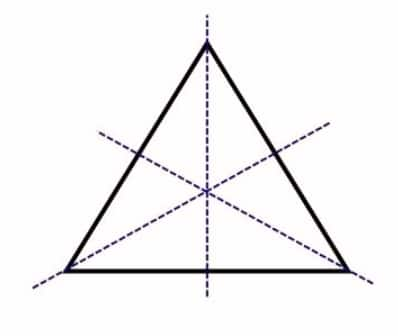
b. A triangle with equal sides and equal angles.
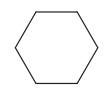
c. A hexagon with equal sides and equal angles.
Solution:
a. 
b. 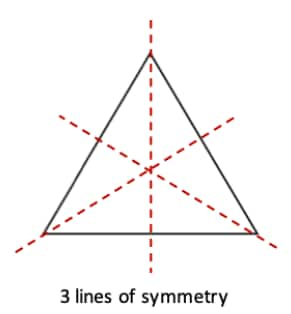
c. 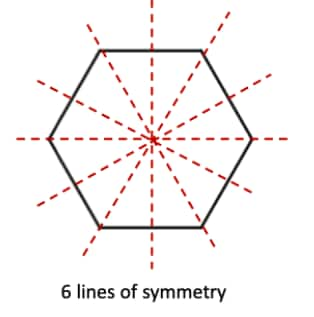
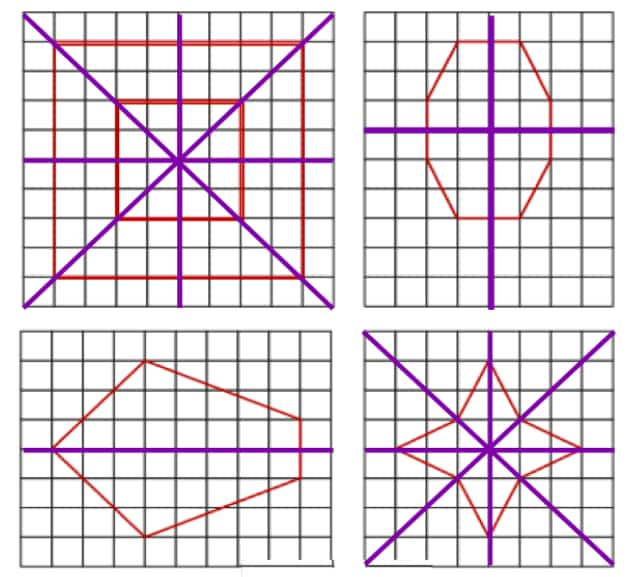
Question 7: Trace each figure and draw the lines of symmetry, if any
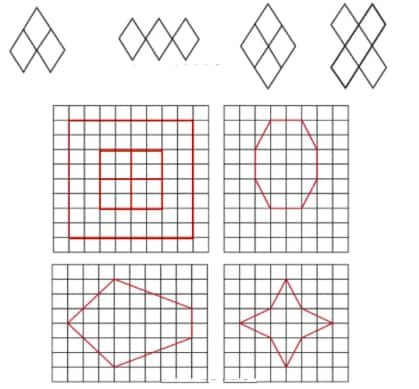
Solution:
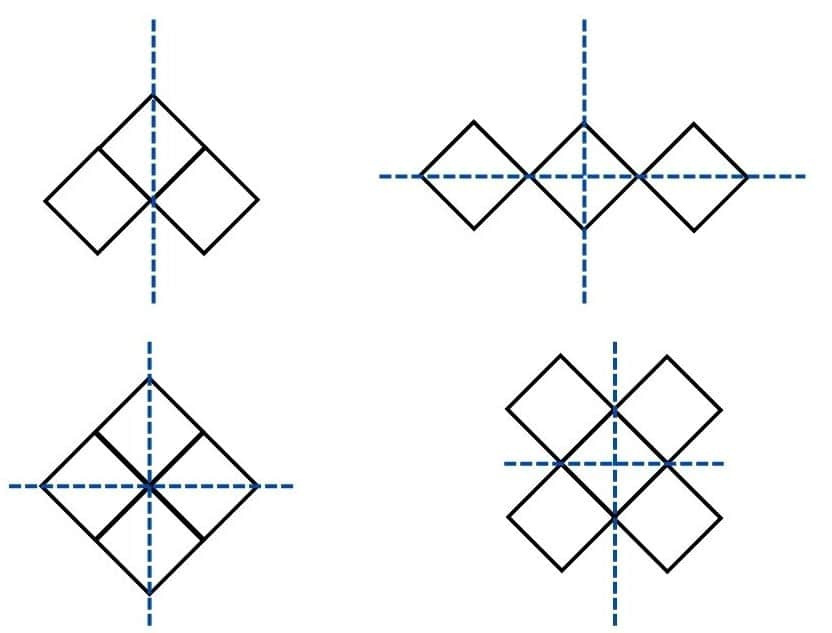
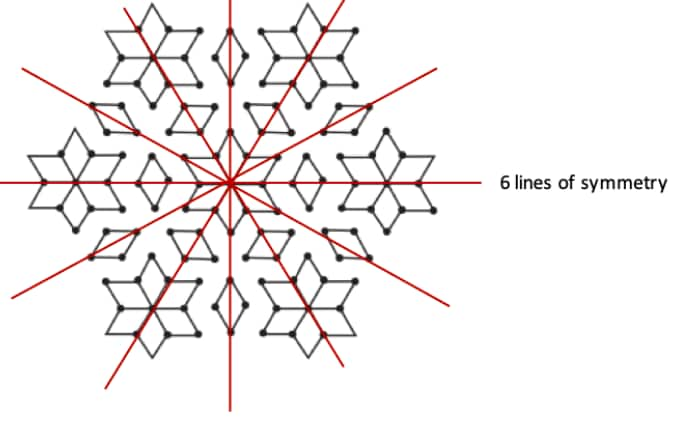
Question 8: Find the lines of symmetry for the kolam below.
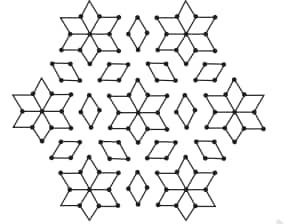
Solution:
Question 9: Draw the following.
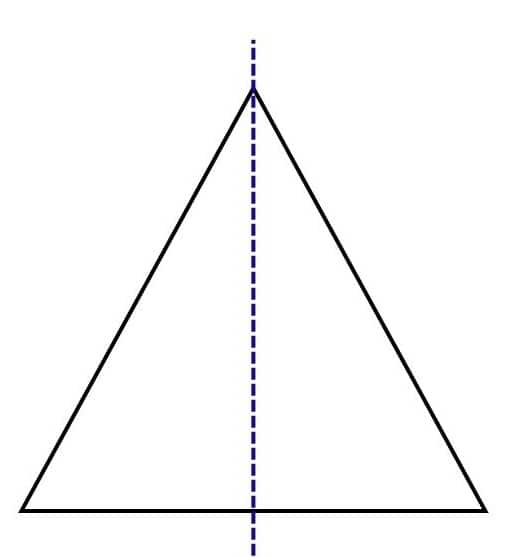
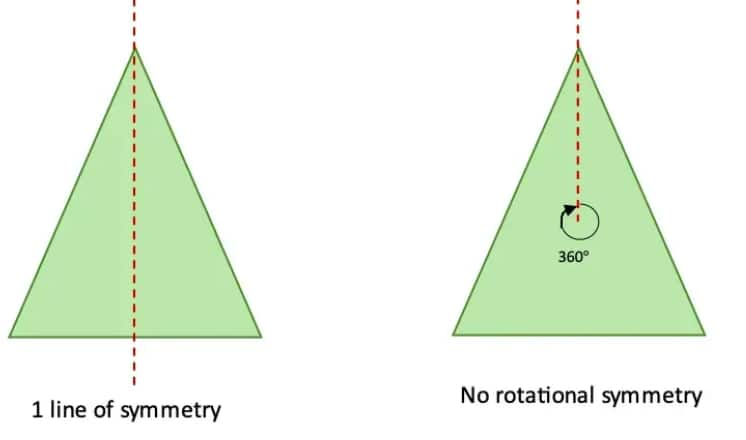
a. A triangle with exactly one line of symmetry.
b. A triangle with exactly three lines of symmetry.
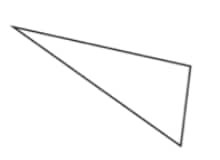
c. A triangle with no line of symmetry. Is it possible to draw a triangle with exactly two lines of symmetry?
Solution:
| Sr. No. |
Types of triangles |
Graphical representation |
| a. |
An isosceles triangle has only 1 line of symmetry. |
|
| b. |
An equilateral triangle has 3 lines of symmetry. |
|
| c. |
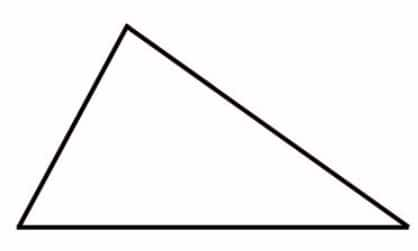
A scalene triangle has no lines of symmetry. |
|
Question 10: Draw the following. In each case, the figure should contain at least one curved boundary.
a. A figure with exactly one line of symmetry.
b. A figure with exactly two lines of symmetry.
c. A figure with exactly four lines of symmetry.
Solution:
| Sr. No. | Description | Figure |
| a. |
A figure with exactly one line of symmetry. |
|
| b. |
A figure with exactly two lines of symmetry. |
|
| c. |
A figure with exactly four lines of symmetry. |
|
Question 11: Copy the following on squared paper. Complete them so that the blue line is a line of symmetry. Problem (a) has been done for you.
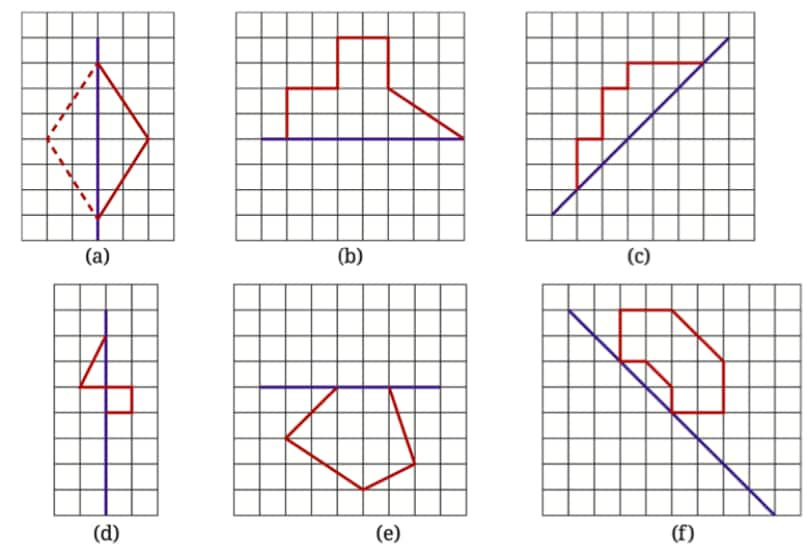
Hint: For (c) and (f), see if rotating the book helps!
Solution:
B. 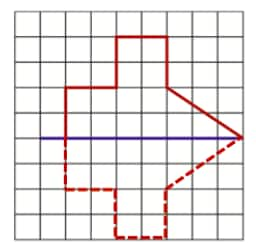
C. 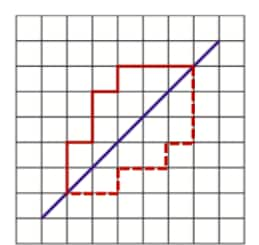
D. 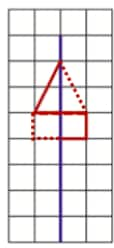
E. 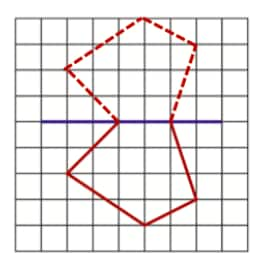
F. 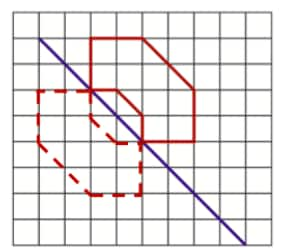
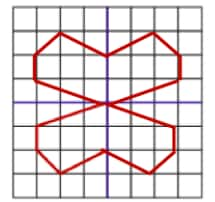
Question 12: Copy the following drawing on squared paper. Complete each one of them so that the resulting figure has the two blue lines as lines of symmetry.
Solution:
a.
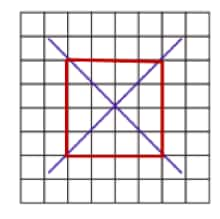
b.
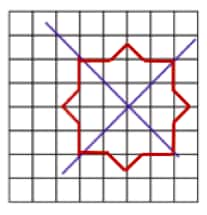
c.
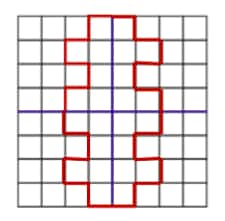
d.
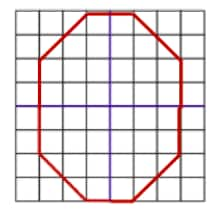
e.
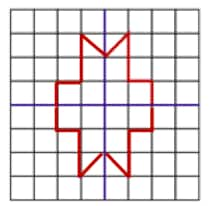
f.
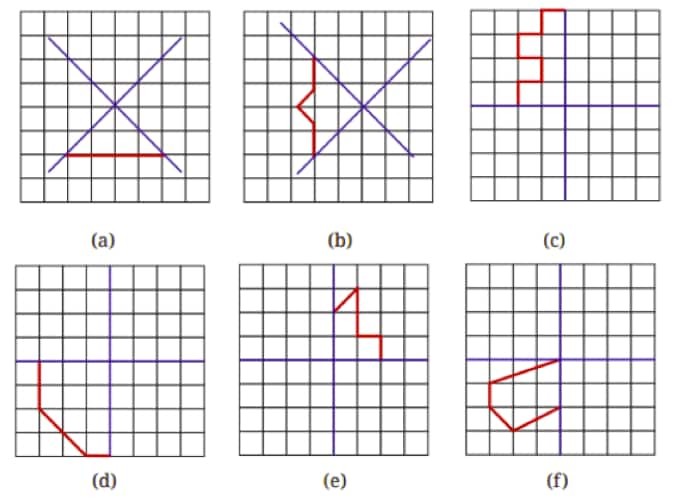
Question 13: Copy the following on a dot grid. For each figure, draw two more lines to make a shape that has a line of symmetry.
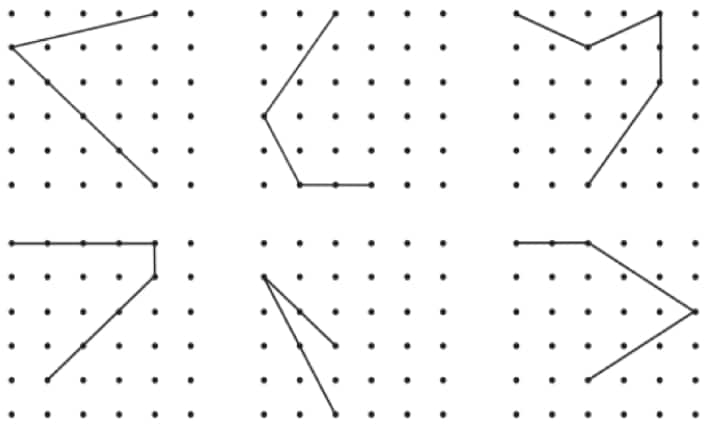
Solution:
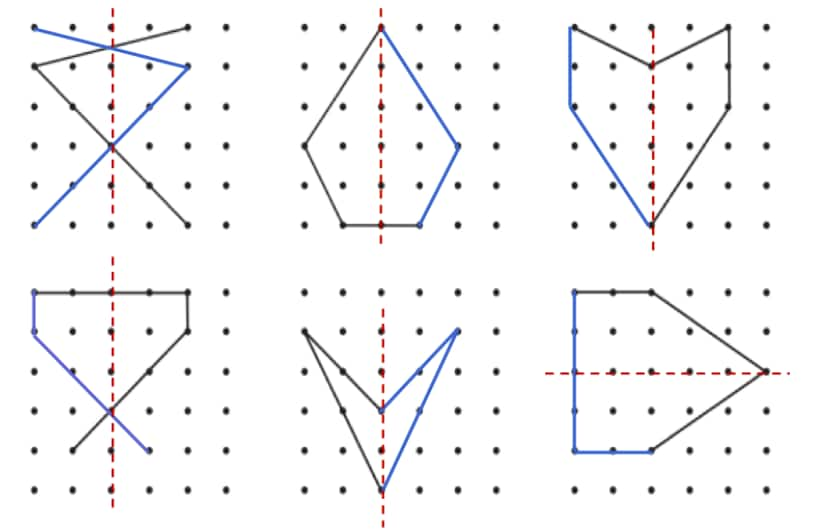
|
Symmetry Class 6 Question Answers |
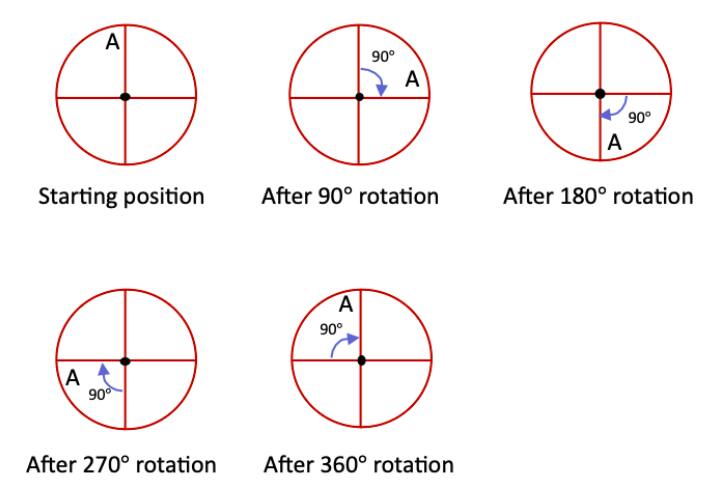
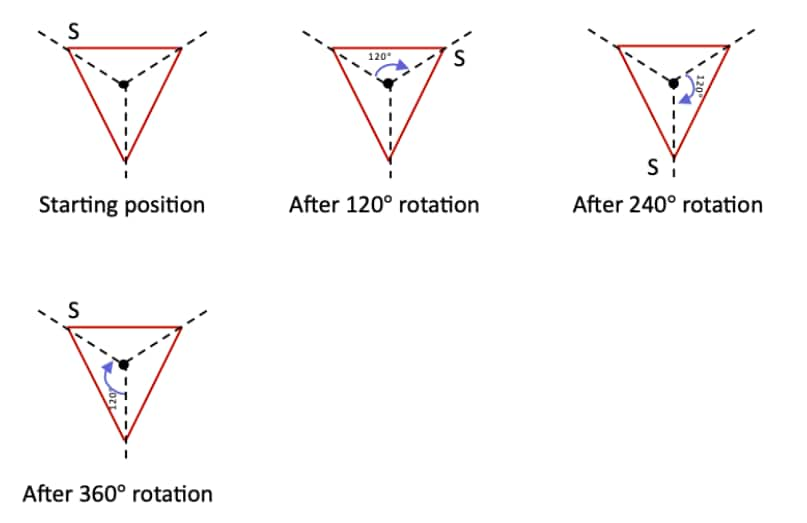
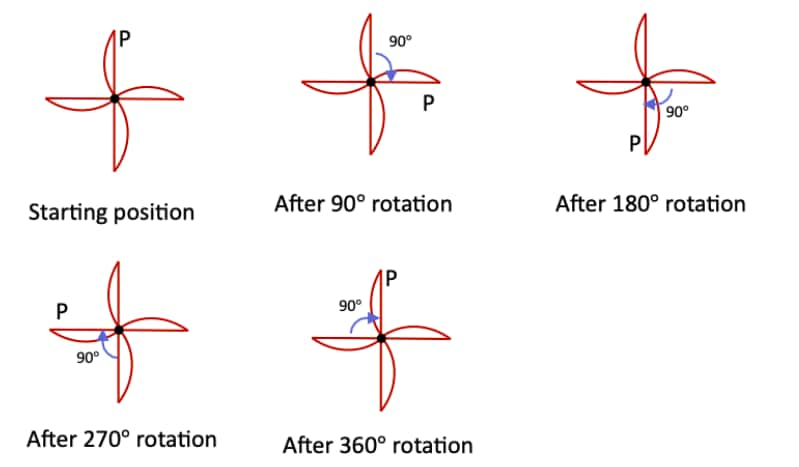
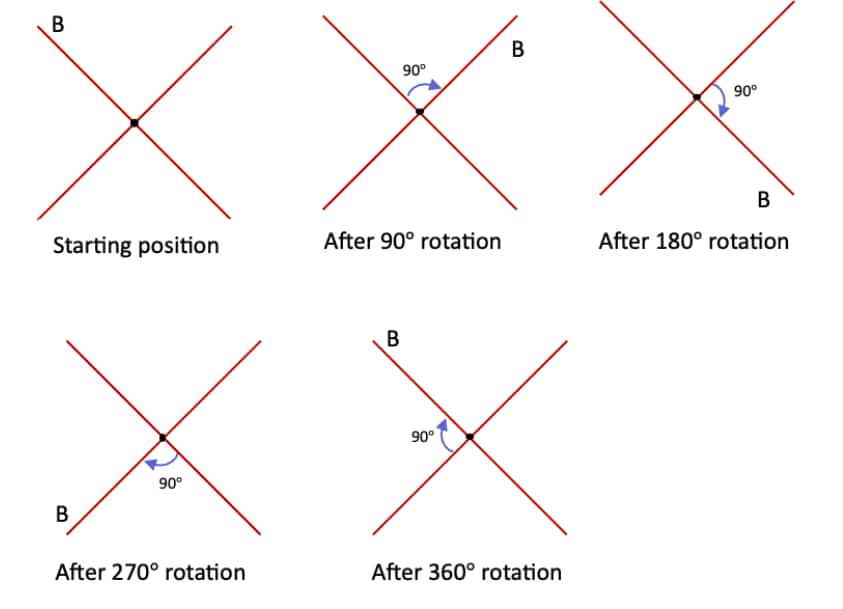
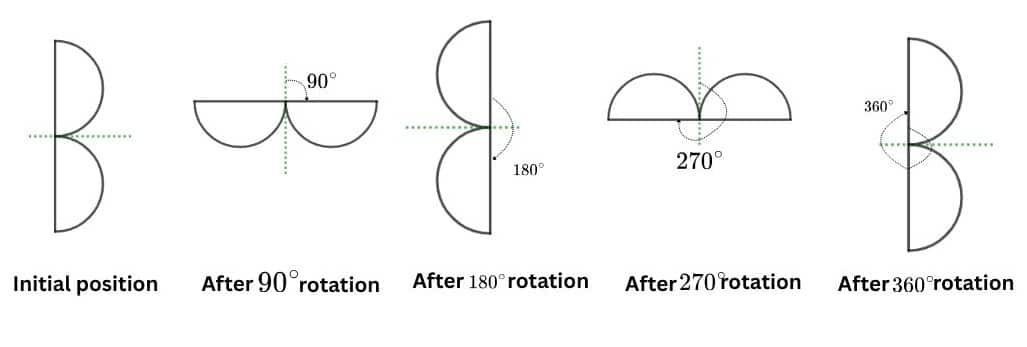
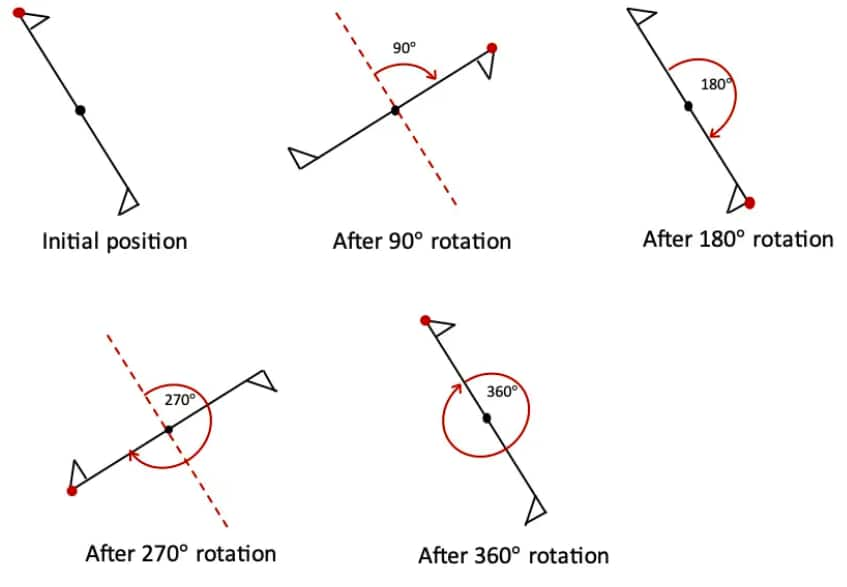
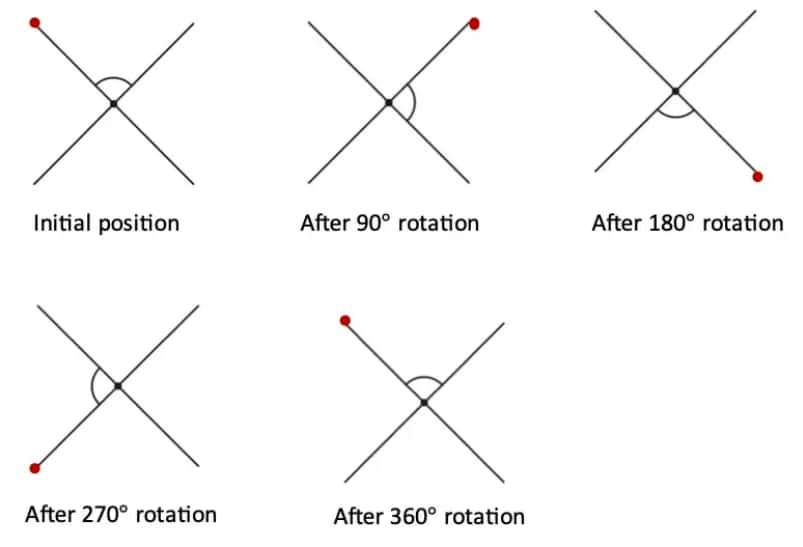
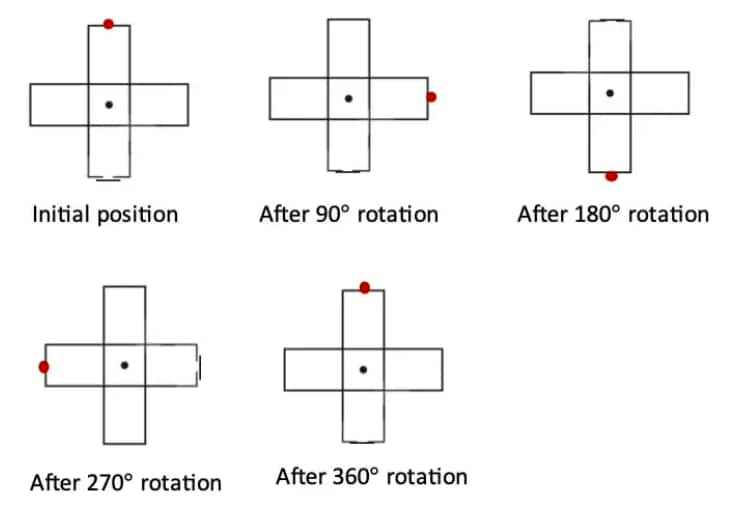
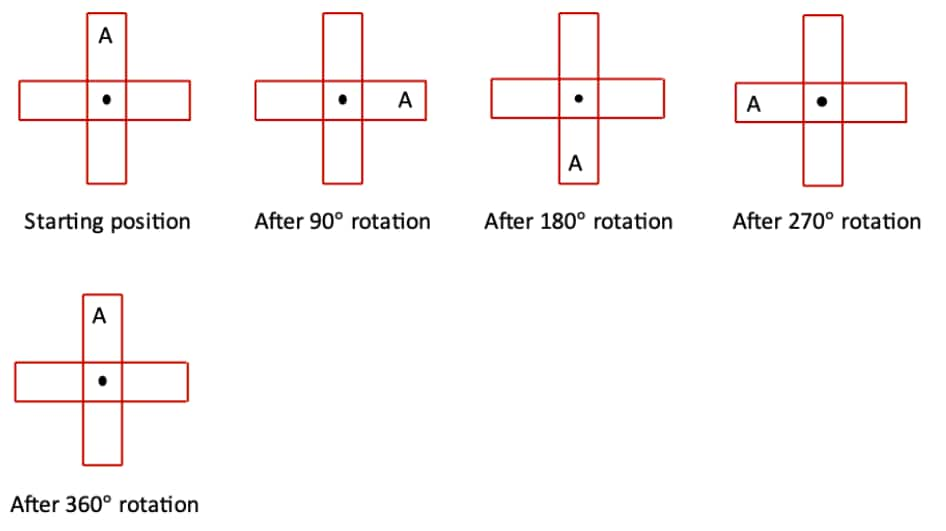
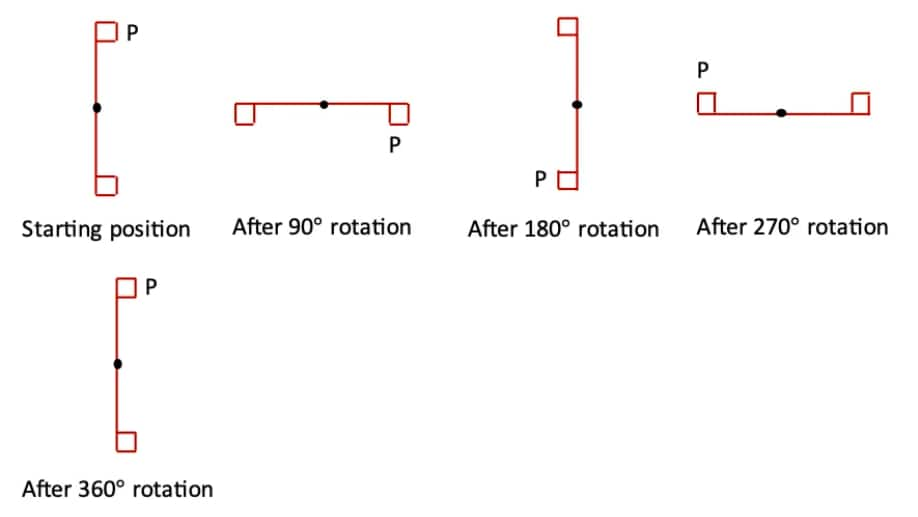
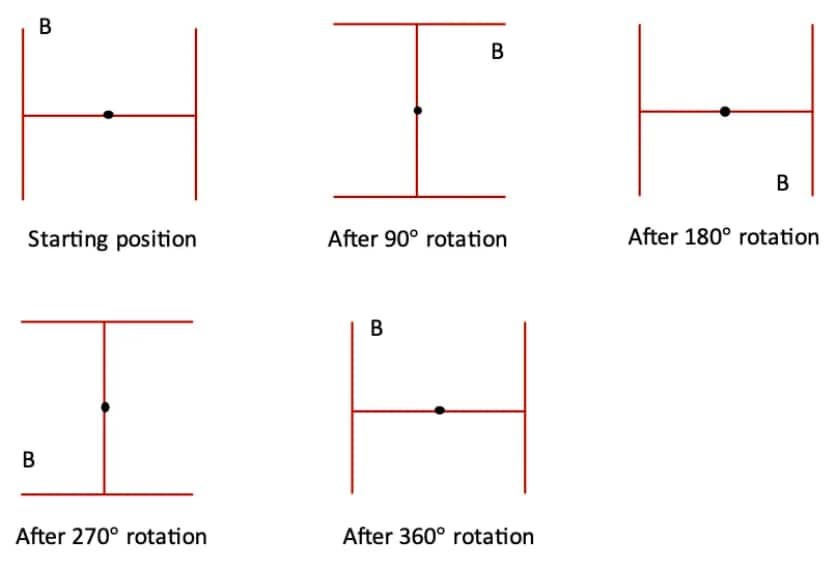
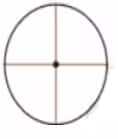
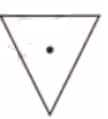
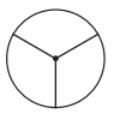
Question 1: Find the angles of symmetry for the given figures about the point marked •.
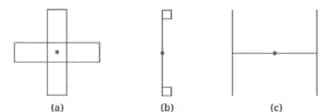
Solution:
a. The initial angle of symmetry in this figure is 90°.
Because after a 90° rotation, the figure remains the same.
∴ The angles of symmetry of the figure are: 90°, 180°, 270°, 360°
b. The angle of symmetry in this figure is 360°.
Because only after a whole 360° rotation, we will get the same figure.
c. The initial angle of symmetry in this figure is 180°.
Because after a 180° rotation, we will get the same figure.
∴ The angles of symmetry of the figure are: 180° and 360°
Question 2: Which of the following figures have more than one angle of symmetry?
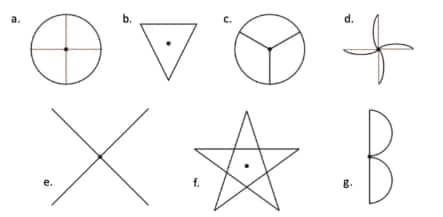
Solution:
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
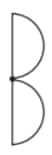 |
|
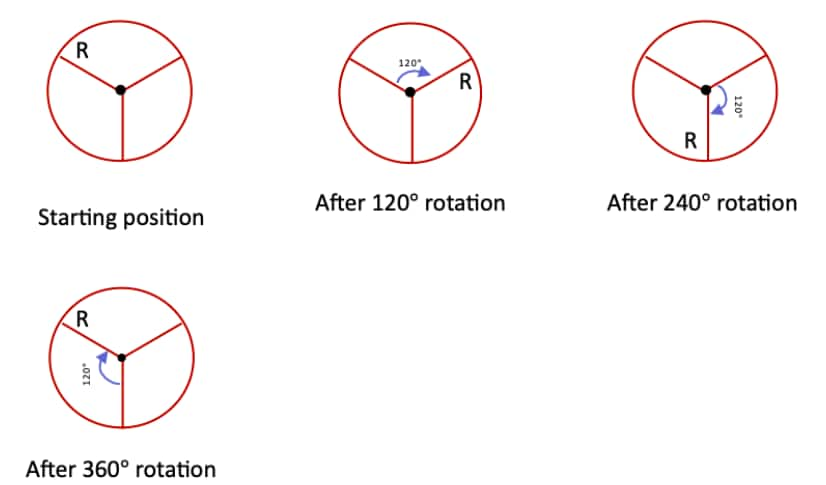
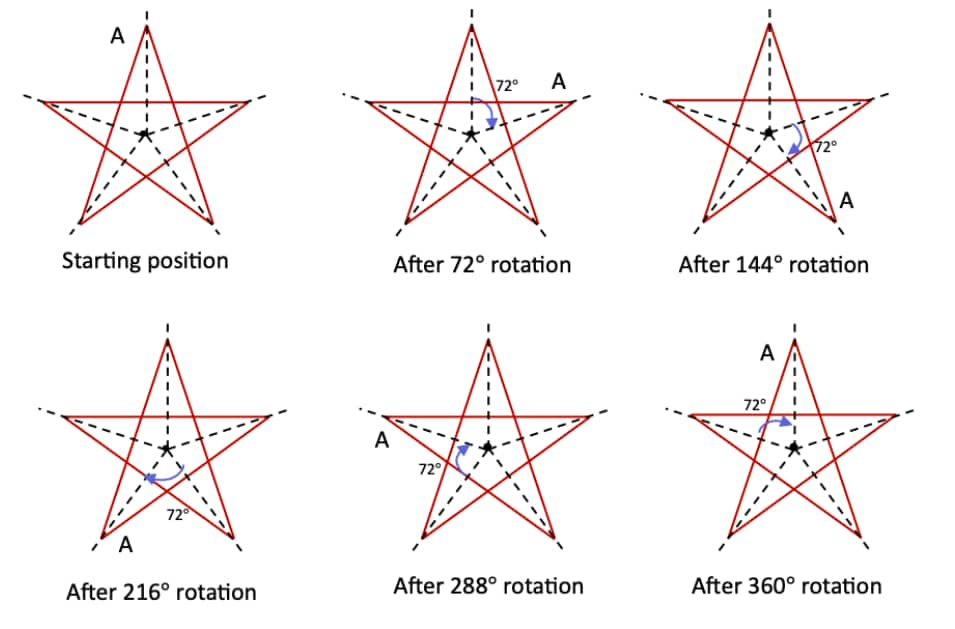
Question 3: Give the order of rotational symmetry for each figure:
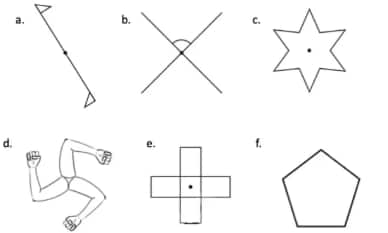
Solution:
 |
|
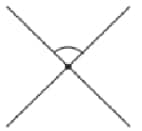 |
|
 |
|
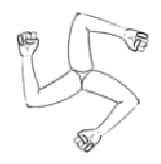 |
|
 |
|
 |
|
| Symmetry Class 6 Question Answers Page number: 238-239 Number of Questions: 11 |
Question 1: Colour the sectors of the circle below so that the figure has
i) 3 angles of symmetry, ii) 4 angles of symmetry, iii) What are the possible numbers of angles of symmetry you can obtain by colouring the sectors in different ways?
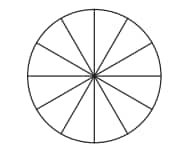
Solution:
(i) 3 angles of symmetry will appear after each 120-degree rotation.
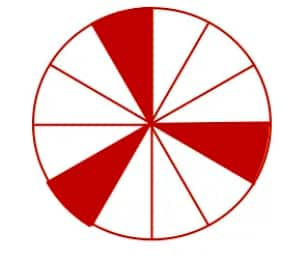
(ii) 4 angles of symmetry will appear after each 90-degree rotation

(iii) We can obtain four possible numbers of symmetry angles by colouring the sectors in different ways.
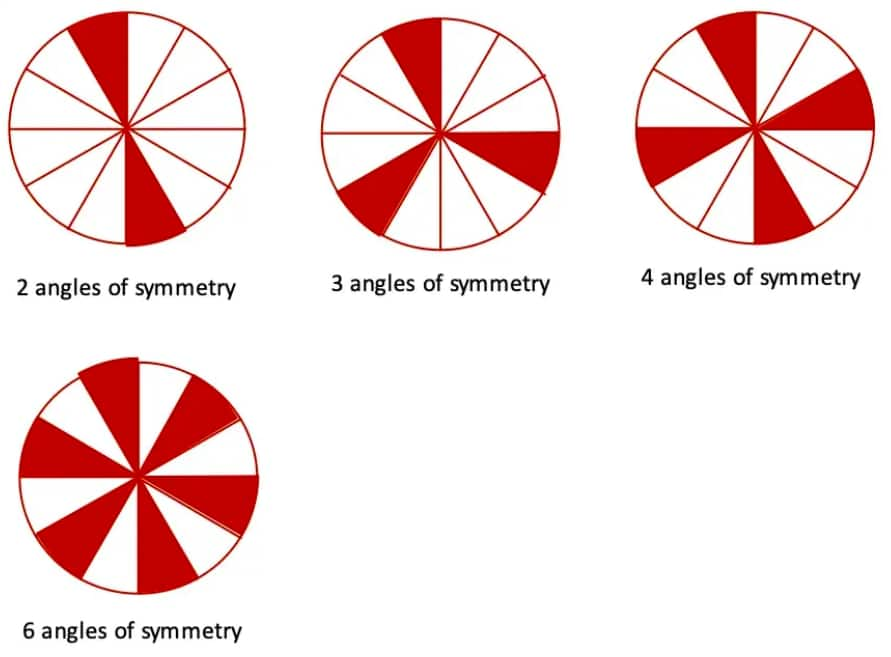
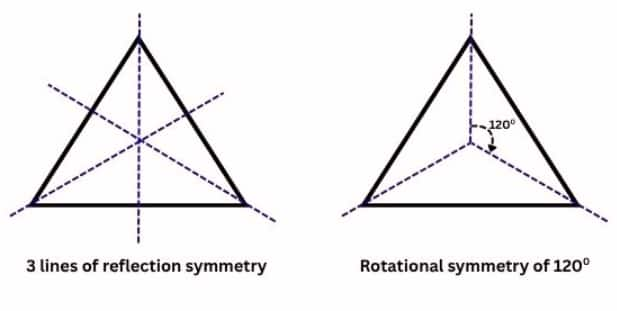
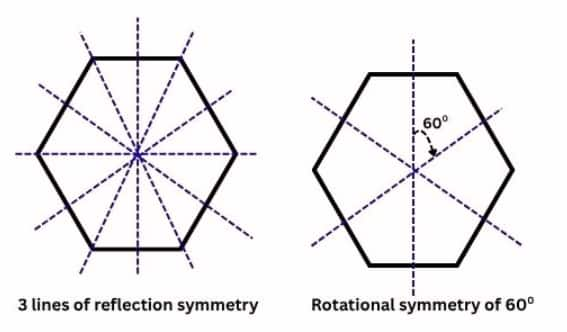
Question 2: Draw two figures other than a circle and a square that have both reflection symmetry and rotational symmetry.
Solution:
|
Equilateral Triangle |
|
|
Regular Hexagon |
|
Question 3: Draw, wherever possible, a rough sketch of:
a. A triangle with at least two lines of symmetry and at least two angles of symmetry.
b. A triangle with only one line of symmetry but not having rotational symmetry.
c. A quadrilateral with rotational symmetry but no reflection symmetry.
d. A quadrilateral with reflection symmetry but not having rotational symmetry.
Solution:
|
A triangle with at least two lines of symmetry and at least two angles of symmetry |
|
|
A triangle with only one line of symmetry, but not having rotational symmetry. |
|
|
A quadrilateral with rotational symmetry but no reflection symmetry. |
|
|
A quadrilateral with reflection symmetry but not having rotational symmetry. |
|
Question 4: In a figure, 60° is the smallest angle of symmetry. What are the other angles of symmetry of this figure?
Solution:
Since 60° is the smallest angle of symmetry, any angle that is a multiple of 60° up to 360° is also an angle of symmetry.
The other angles of symmetry would be multiples of 60°, i.e. 120°,180°,240°,300° and 360°.
Question 5: In a figure, 60° is an angle of symmetry. The figure has two angles of symmetry less than 60°. What is its smallest angle of symmetry?
Solution:
Smallest angle of symmetry = $\frac{60°}3=20°$
Question 6: Can we have a figure with rotational symmetry whose smallest angle of symmetry is:
a. 45°?
b. 17°?
Solution:
(a) 360°÷45° = 8.
Since 45° divides 360° perfectly, it's possible to have a figure with rotational symmetry whose smallest angle of symmetry is 45°.
(b) 360°÷17°=21.18
Since 17° doesn't evenly divide 360°, it is impossible to have a figure with rotational symmetry whose smallest angle of symmetry is 17°.
Question 7: This is a picture of the new Parliament Building in Delhi.

a. Does the outer boundary of the picture have reflection symmetry? If so, draw the lines of symmetries. How many are they?
b. Does it have rotational symmetry around its centre? If so, find the angles of rotational symmetry.
Solution:
a. Yes, the outer boundary of the picture has reflection symmetry. There are three lines of symmetry, and it is shown in the figure below.
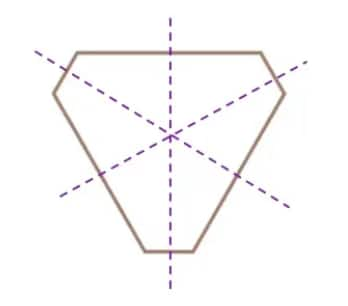
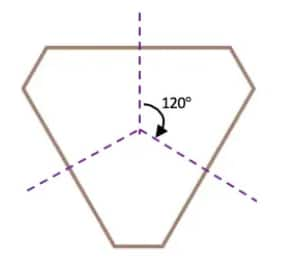
b. Yes, the figure has rotational symmetry around its centre.
The smallest angle of rotational symmetry $= \frac{360°}3=120°$
Therefore, the angles of rotational symmetry of the figure are 120°,240° and 360°.
Question 8: How many lines of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
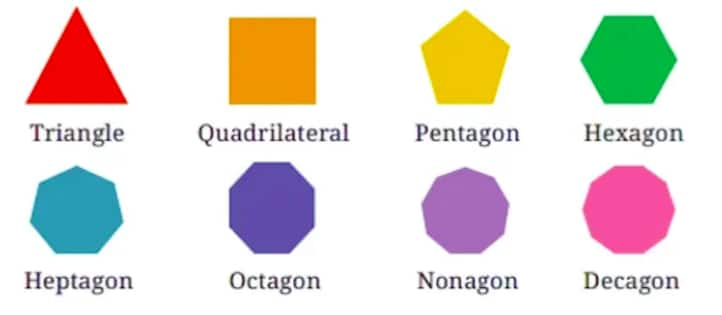
Solution:
In a regular polygon, the number of lines of symmetry equals the number of its sides.
Therefore, the Number of lines of symmetry in a triangle (3-sided polygon) = 3
Number of lines of symmetry in a quadrilateral (4-sided polygon) =4
Number of lines of symmetry in a pentagon (5-sided polygon) =5
Number of lines of symmetry in a hexagon (6-sided polygon) = 6
Number of lines of symmetry in a heptagon (7-sided polygon) =7
Number of lines of symmetry in an octagon (8-sided polygon) =8
Number of lines of symmetry in a nonagon (9-sided polygon) =9
Number of lines of symmetry in a decagon (10-sided polygon) = 10
Number sequence: 3,4,5,6,7,8,9,10…..
Question 9: How many angles of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
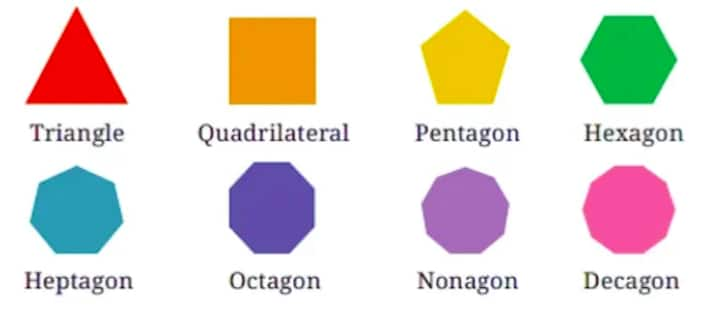
Solution:
In a regular polygon, the number of angles of symmetry is equal to the number of lines of symmetry.
Therefore,
Number of angles of symmetry in a triangle (3-sided polygon) =3
Number of angles of symmetry in a quadrilateral (4-sided polygon) =4
Number of angles of symmetry in a pentagon (5-sided polygon) =5
Number of angles of symmetry in a hexagon (6-sided polygon) =6
Number of angles of symmetry in a heptagon (7-sided polygon) =7
Number of angles of symmetry in an octagon (8-sided polygon) =8
Number of angles of symmetry in a nonagon (9-sided polygon) = 9
Number of angles of symmetry in a decagon (10-sided polygon) = 10
Number sequence: 3,4,5,6,7,8,9,10…..
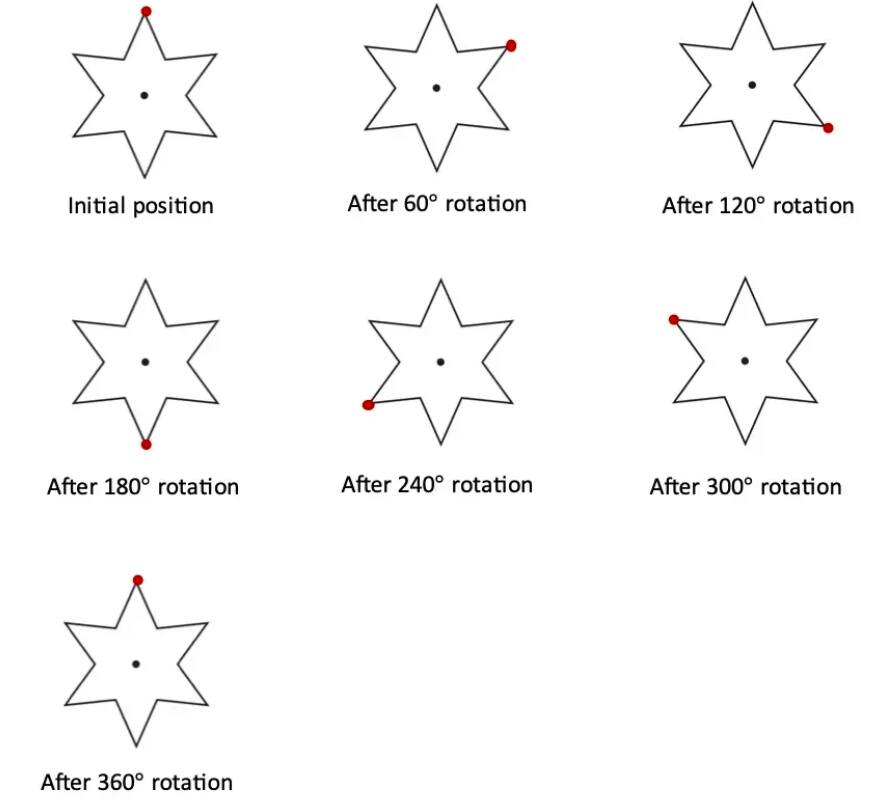
Question 10: How many lines of symmetry do the shapes in the last shape sequence in Chapter 1, Table 3, the Koch Snowflake sequence, have? How many angles of symmetry?
Solution:
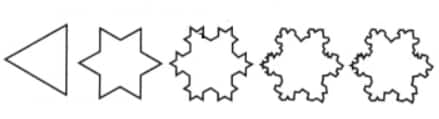
The triangular shape has 3 lines of symmetry and 3 angles of symmetry.
In six-pointed stars, the lines of symmetry are 12 and the angle of symmetry is 6.
The lines of symmetry and angle of symmetry for the remaining three figures are the same as those of a six-pointed star.
Question 11: How many lines of symmetry and angles of symmetry does the Ashoka Chakra have?

Solution:
The Ashoka Chakra has 24 spokes spread equally.
24 spokes make 12 pairs.
A line through an opposite pair is a line of symmetry.
Hence, there are 12 lines of symmetry.
Smallest angle of symmetry =$\frac{360°}{12}=30°$
Other angles of symmetry are its multiples up to 360°.
Other angles are 60°,120°,150°, 360°. (12 angles in all).
NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Notes
Careers360 has prepared these Class 6 Symmetry Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Symmetry NCERT solutions and solve them independently from next time.
Symmetry: Symmetry refers to a part or parts of a figure that are repeated in some definite pattern.

In the above image, we see that the pattern is repeated after a fixed interval. This is a symmetrical pattern.
Line of Symmetry: A line of symmetry is one that differentiates an object into 2 equal halves, such that the right-hand side is equal to the left-hand side or the image in the top matches that in the bottom. A line that cuts a figure into two parts that exactly overlap when folded along that line is called a line of symmetry of the figure.
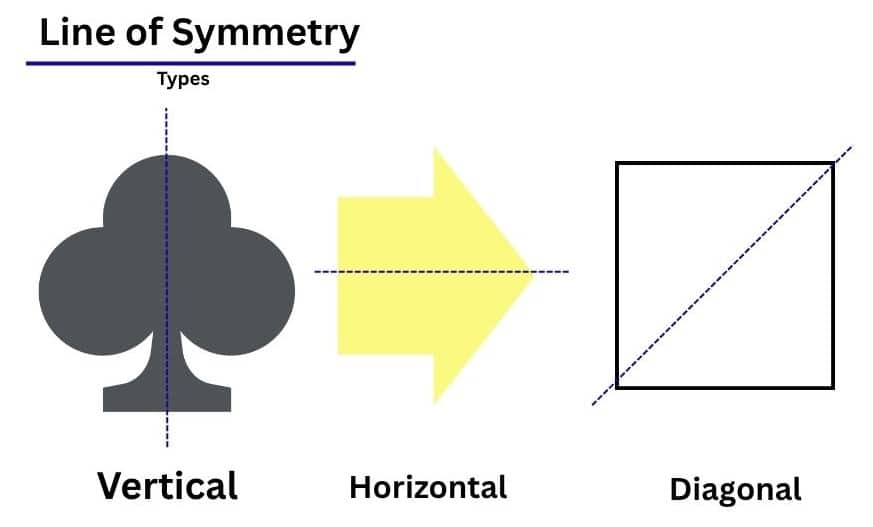
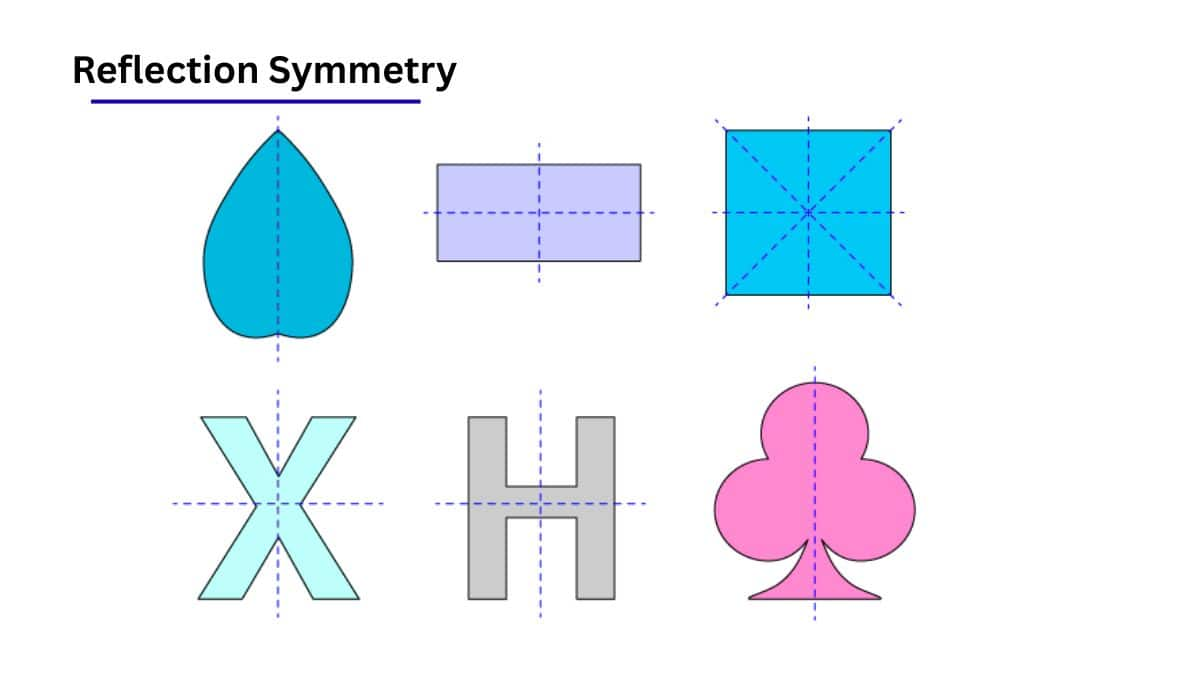
Reflection: Reflection of an object is defined as the exact copy of that object. It is the same object that completely overlaps the first one. A figure that has a line or lines of symmetry is thus also said to have reflection symmetry.
Rotational Symmetry: When we define rotational symmetry, we can say that it is determined on a fixed point known as the centre of rotation. The angle through which it is rotated is known as the angle of rotation. Eg windmill.
NCERT Symmetry Class 6 Maths Chapter 9: Topics
Topics you will learn in NCERT Class 6 Maths Chapter 9 Symmetry include:
9.1 Line of Symmetry
9.2 Rotational Symmetry
Class 6 Maths Chapter 9 Symmetry solutions: Extra Question
Question:
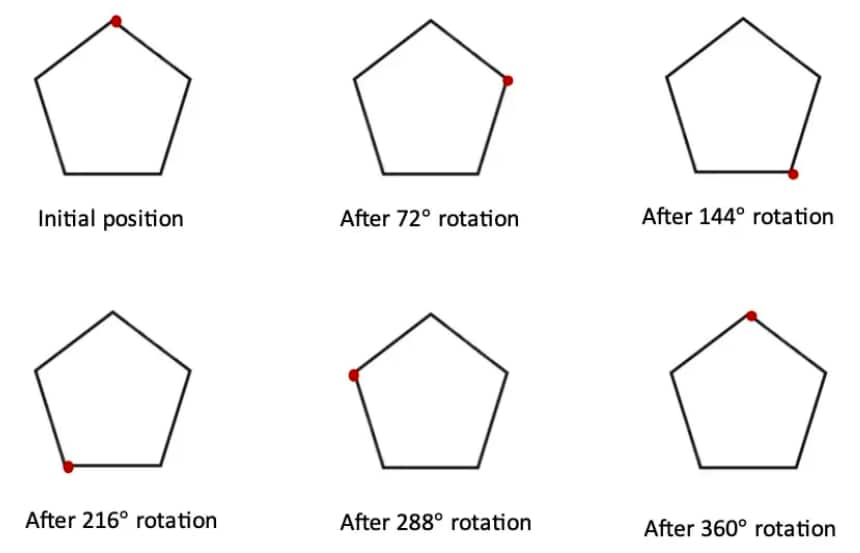
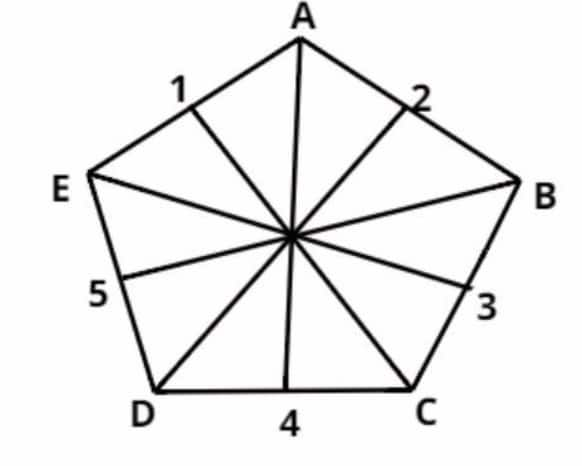
How many lines of symmetry does a regular pentagon have? Draw the pentagon and its lines of symmetry.
Solution:
A regular pentagon has 5 lines of symmetry. Each line of symmetry passes through one vertex of the pentagon and the midpoint of the opposite side.
NCERT Solutions for Class 6 Maths Chapter 9 Symmetry: Points to Remember
Check the following important points to understand and solve the Class 6 Maths Chapter 9 Symmetry question answers effectively.
Symmetry: Symmetry refers to a part or parts of a figure that are repeated in some pattern.
Line of Symmetry: A line that cuts a figure into two parts that exactly overlap when folded along that line is called a line of symmetry of the figure.
Reflection: Reflection of an object is defined as the exact copy of that object. It is the same object that completely overlaps the first one.
Rotational Symmetry: When we define rotational symmetry, we can say that it is defined on a fixed point known as the centre of rotation. The angle through which it is rotated is known as the angle of rotation.
Why are Class 6 Maths Chapter 9 Symmetry question answers important?
In Chapter 8 of Class 6, Symmetry, students understand balanced shapes and patterns through the concepts of symmetry. Here are some more points on why the Class 6 Maths Symmetry question answers are important.
- This chapter improves the ability to identify symmetrical figures in daily life.
- These symmetry question answers develop logical reasoning through pattern recognition.
- Also, practising questions from this chapter improves accuracy and observation skills by finding symmetrical lines in objects and patterns.
- Board exams and competitive exams regularly feature questions about symmetry.
NCERT Solutions for Class 6 Maths Chapter Wise
For students' preparation, Careers360 has gathered all Class 6 Maths NCERT solutions here for quick and convenient access.
NCERT Books and Syllabus
Students can also check the NCERT Books and the latest NCERT Syllabus for Class 6 here:
Frequently Asked Questions (FAQs)
Certainly. Shapes such as squares, circles, and regular polygons have multiple lines of symmetry.
Yes, shapes like circles and regular polygons show both types of symmetry.
No, a scalene triangle has no lines of symmetry because all sides and angles are different.
Yes, symmetry is seen in objects like leaves, butterflies, buildings, designs, and even alphabets.
A line of symmetry divides a shape into two equal and identical halves, like a mirror image.
A figure has rotational symmetry if it looks the same after being rotated (turned) around a central point by a certain angle.
NCERT Class 6 Maths Chapter 9 Symmetry helps students understand the concept of symmetry, lines of symmetry, and how symmetrical patterns are used in daily life.
Yes, many educational platforms, such as Careers360, offer free downloadable PDFs of NCERT Symmetry Class 6 Solutions. Students can find the free downloadable PDF in this article itself.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters