NCERT Solutions for Class 6 Maths Chapter 7 - Fractions
Have you ever tried to share a pizza with your friends? Congratulations, you’ve already used fractions in real life. In the world of numbers, fractions are the art of splitting and still staying connected. Fractions are the bridge between division and multiplication. We are surrounded by fractions on all our sides. Fractions are an integral part of our lives. Fractions are a part of a whole. If we share a single chocolate among two people, each person gets half of the chocolate, which is a part of a whole. This NCERT Solutions for class 6 article contains the answers to all the questions in this chapter in a comprehensive, step-by-step manner. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 7 Fractions: Download Free PDF
- NCERT Solutions for Class 6 Maths Chapter 7 Fractions: Exercise
- NCERT Fractions Class 6 Maths Chapter 7 - Topics
- Class 6 Maths Chapter 7 Fractions solutions: Extra Question
- NCERT Solutions for Class 6 Maths Chapter 7 Fractions: Notes
- NCERT Solutions for Class 6 Maths Chapter 7 Fractions - Points to Remember
- Why are Class 6 Maths Chapter 7 Fractions question answers important?
- NCERT Solutions for Class 6 Maths Chapter Wise
- NCERT Books and Syllabus

Fractions help us realise that even small parts can add up to something whole. Mastering fractions is the first step to solving many real-life maths problems. These NCERT Solutions for Class 6 Maths are highly reliable resources, as they were created by experienced subject matter experts from Careers360. Students can use these solutions to practice more questions and check their answers during exam preparation, identifying their weaknesses and areas for improvement later. For detailed solutions, complete syllabus notes, and a free PDF download, refer to this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 7 Fractions: Download Free PDF
Careers360 brings you NCERT Class 6 Maths Chapter 7 Fractions solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 7 Fractions: Exercise
Below are the detailed Class 6 Maths Chapter 7 Fractions question answers provided in the textbook.
|
Fractions Class 6 Question Answers |
Fill in the blanks with fractions.
Question 1: Three guavas together weigh 1 kg. If they are roughly of the same size, each guava will roughly weigh ____ kg.
Answer:
Given, weigh of 3 guavas $=1 \mathrm{~kg}$,
then weigh of each of the guava $=\frac{\text { total weight }}{3}=\frac{1}{3} \mathrm{~kg}$
Question 2: A wholesale merchant packed 1 kg of rice in four packets of equal weight. The weight of each packet is ___ kg.
Answer:
1 kg of rice is packed in 4 packets of equal weight, then the weight of each packet is
$
=\frac{\text { Total weight }}{\text { No. of packets }}=\frac{1}{4} \mathrm{~kg} .
$
Question 3: Four friends ordered 3 glasses of sugarcane juice and shared them equally among themselves. Each one drank ____ glass of sugarcane juice.
Answer:
The Amount of sugarcane consumed by four friends = 3 glasses.
Amount of sugarcane consumed by each friend $=\frac{3}{4}$ glass.
Hence, each one drank $\frac{3}{4}$ glass of sugarcane juice.
Question 4: The big fish weighs $\frac{1}{2} \mathrm{~kg}$. The small one weighs $\frac{1}{4} \mathrm{~kg}$. Together they weigh _______ kg.
Answer:
Given the weighs of big fish $=\frac{1}{2} \mathrm{~kg}$ and the weighs of small fish $=\frac{1}{4} \mathrm{~kg}$
Total weight of both fish $=\frac{1}{2} + \frac{1}{4}=\frac{2+1}{4} \mathrm{~kg}$ $=\frac{3}{4} \mathrm{~kg}$
Question 5: Arrange these fraction words in order of size from the smallest to the biggest in the empty box below: One and a half, three-quarters, one and a quarter, half, quarter, two and a half.
Answer:
One and a half means $1+\frac{1}{2}=1 \frac{1}{2}$.
Three-quarters means $\frac{3}{4}$.
One and a quarter means $1+\frac{1}{4}=1 \frac{1}{4}$.
Half means $\frac{1}{2}$.
Quarter means $\frac{1}{4}$
Two and a half mean $2+\frac{1}{2}=2 \frac{1}{2}$.
Now, arranging the fraction words in order of size from the smallest to the biggest parts: Quarter < Half < Three Quarters < One and a quarter < One and a half < Two and a half.
|
Fractions Class 6 Question Answers |
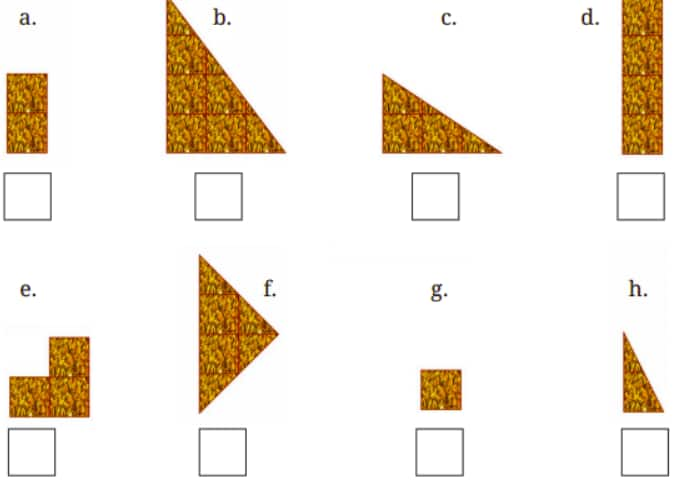
Question 1: The figures below show different fractional units of a whole chikki. How much of a whole chikki is each piece?
Answer:
a) We get this piece by breaking the chikki into 12 equal parts.
Hence, it is $\frac 1{12}$
b) We get this piece by breaking the chikki into 4 equal parts.
Hence, it is $\frac14$
c) We get this piece by breaking the chikki into 8 equal parts.
Hence, it is $\frac18$
d) We get this piece by breaking the chikki into 6 equal parts.
Hence, it is $\frac16$
e) We get this piece by breaking the chikki into 8 equal parts.
Hence, it is $\frac18$
f) We get this part by breaking the chikki into 6 equal pieces.
Hence, it is $\frac16$
g) We get this part by breaking the chikki into 24 equal pieces.
Hence, it is $\frac1{24}$
h) We get this part by breaking the chikki into 24 equal pieces.
Hence, it is $\frac1{24}$
|
Fractions Class 6 Question Answers |
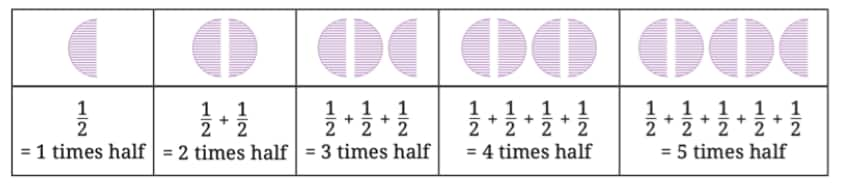
Question 1: Continue this table of $\frac{1}{2}$ for 2 more steps.
Answer:
Here,  represents a full roti (whole)
represents a full roti (whole)
Step 1:
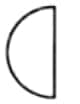
$=\frac{1}{2}=1$ times half
Step 2:
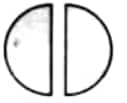
$=\frac{1}{2}+\frac{1}{2}=2$ times half
Step 3:

$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=3$ times half
Step 4:
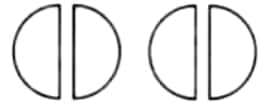
$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=4$ times half
Step 5:
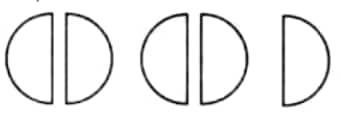
$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=5$ times half
Step 6:

$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=6$ times half $=6 \times \frac{1}{2}=\frac{6}{2}=3$
Step 7:

$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=7$ times half $=7 \times \frac{1}{2}=\frac{7}{2}$
Question 2: Can you create a similar table for $\frac{1}{4} ?$
Answer:
Yes, we can create a similar table for $\frac{1}{4}.$
Here
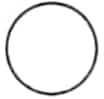
represents a full roti (whole).
|
| $\frac{1}{4}=1$ times quarter |
|
| $\frac{2}{4}=2$ times quarter |
|
| $\frac{3}{4}=3$ times quarter |
|
| $\frac{4}{4}=4$ times quarter |
|
| $\frac{5}{4}=5$ times quarter |
|
| $\frac{6}{4}=6$ time quarter |
|
| $\frac{7}{4}=7$ times quarter |
|
| $\frac{8}{4}=8$ times quarter |
Question 3: Make $\frac{1}{3}$ using a paper strip. Can you use this to also make $\frac{1}{6}$?
Answer: Yes, we can use this $\frac{1}{3}$ to make $\frac{1}{6}$.
Take a strip of paper.
Fold the strip into three equal parts and then open it up.
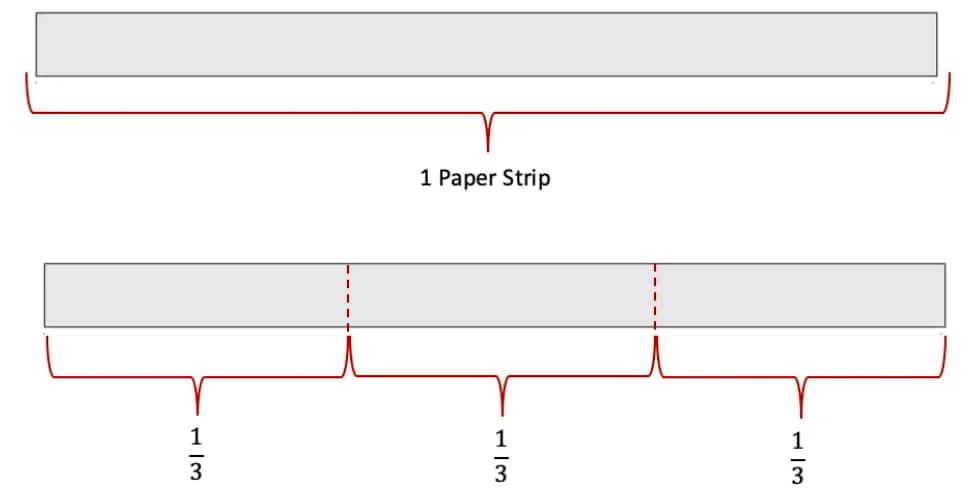
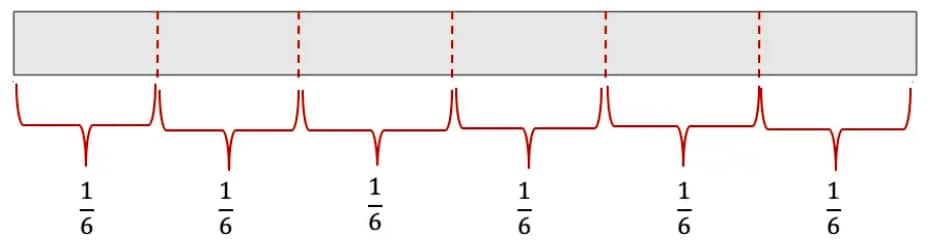
When we divide each part of this $\frac{1}{3}$ it is equal to Half of $\frac{1}{3}=\frac{1}{3} \times \frac{1}{2}=\frac{1}{6}$
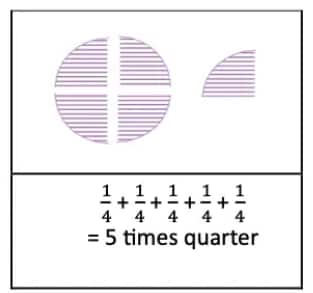
Question 4: Draw a picture and write an addition statement as above to show:
a. 5 times $\frac{1}{4}$ of a roti
b. 9 times $\frac{1}{4}$ of a roti
Answer:
a)
5 times $\frac{1}{4}$ of a roti
$
=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{5}{4}
$
Which means 1 full and $\frac{1}{4}$ roti.
b)
9 times $\frac{1}{4}$ of a roti
$
=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{9}{4}
$
Which means 2 full and $\frac{1}{4}$ of roti.

Question 5: Match each fractional unit with the correct picture:
$\frac{1}{3} \frac{1}{5} \frac{1}{8} \frac{1}{6}$

Answer:
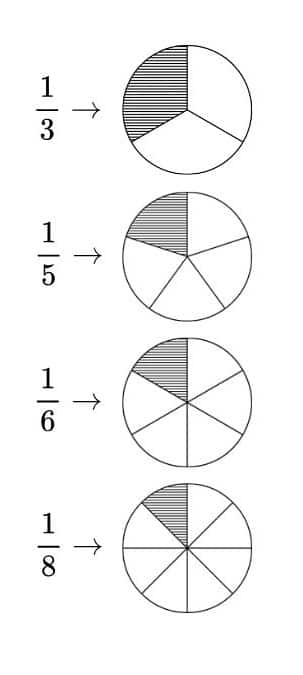
|
Fractions Class 6 Question Answers |
Question 1: On a number line, draw lines of lengths $\frac{1}{10}, \frac{3}{10}$, and $\frac{4}{5}$.
Answer:
Step 1. Draw a line I. Mark a point O on it.
Step 2. Mark point A at a distance of 1 unit from 0.
Step 3. Divide OA into 10 equal parts.
Here, OP represents $\frac{1}{10^2}, \mathrm{OQ}$ represents $\frac{3}{10}$, and OR represents $\frac{8}{10}=\frac{4}{5}$
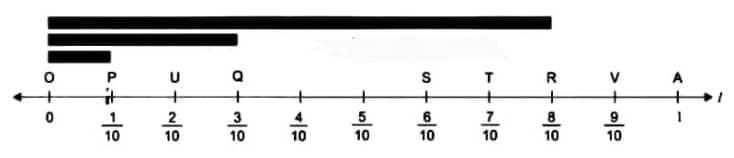
Question 2: Write five more fractions of your choice and mark them on the number line.
Answer:
Step 1. Let a number line OJ be divided into 10 equal parts.
Step 2. Now mark points A, B, C, D,..., J on it.
Step 3. Here
OF represents $\frac{6}{10}=\frac{3}{5}$
OG represents $\frac{7}{10}$
OB represents $\frac{2}{10}=\frac{1}{5}$
OH represents $\frac{8}{10}=\frac{4}{5}$
Ol represents $\frac{9}{10}$
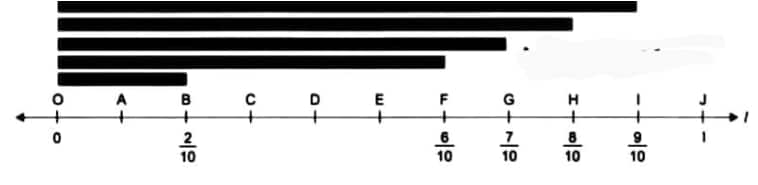
Question 3: How many fractions lie between 0 and 1? Think, discuss with your classmates, and write your answer.
Answer: There are an infinite number of fractions between 0 and 1.
Example: $\frac{3}{5}, \frac{4}{5}, \frac{7}{10}, \frac{1}{2}$ etc.
Question 4: What is the length of the blue line and black line shown below? The distance between 0 and 1 is 1 unit long, and it is divided into two equal parts. The length of each part is $\frac{1}{2}$. So the blue line is $\frac{1}{2}$ units long. Write the fraction that gives the length of the black line in the box.
Answer:
Length of black line is $\frac{1}{2}$.
Length of black line is $\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$
Fraction that gives length of black line $=\frac{3}{2}$

Question 5: Write the fraction that gives the lengths of the black lines in the respective boxes.
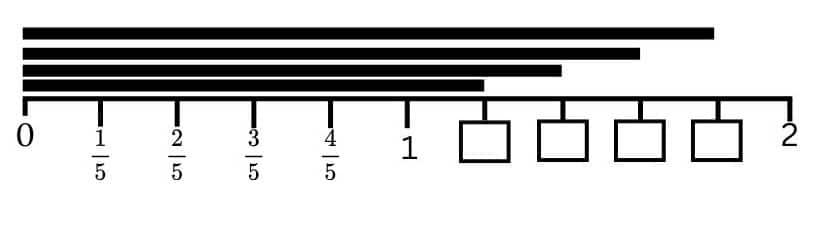
Answer:

|
Fractions Class 6 Question Answers |
Question 1: How many whole units are there in $\frac{7}{2}$?
Answer:
$ \frac{7}{2}=7 \text { times } \frac{1}{2} $
$=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$
$ =\frac{1+1}{2}+\frac{1+1}{2}+\frac{1+1}{2}+\frac{1}{2}$
$ =1+1+1+\frac{1}{2} $
$ =3+\frac{1}{2}$
$ =3 \frac{1}{2}$
Hence, 3 whole units are there in $\frac{7}{2}$.
Question 2: How many whole units are there in $\frac{4}{3}$ and in $\frac{7}{3}$?
Answer:
Here $\frac{4}{3}=4$ times $\frac{1}{3}=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}$
$
\begin{gathered}
=\frac{1+1+1}{3}+\frac{1}{3} \\
=1+\frac{1}{3}=1 \frac{1}{3}
\end{gathered}
$
Hence, 1 whole unit is there in $\frac{4}{3}$.
$\frac{7}{3}= 7 \text { times } \frac{1}{3} $
$ =\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3} $
$ =\frac{1+1+1}{3}+\frac{1+1+1}{3}+\frac{1}{3} $
$ =1+1+\frac{1}{3}$
$=2+\frac{1}{3}$
$=2 \frac{1}{3}$
Hence, 2 whole units are therein $\frac{7}{3}$.
|
Fractions Class 6 Question Answers |
Question 1: Figure out the number of whole units in each of the following fractions:
a. $\frac{8}{3}$
b. $\frac{11}{5}$
C. $\frac{9}{4}$
Answer:
a) Numerator 8 is split/divided into as many 3 's, i.e., denominator number:
$
8=3+3+2=1+1+\frac{2}{3}=2 \frac{2}{3}
$
$\therefore$ No. of whole units in $\frac{8}{3}=2$ whole units.
b)
$\frac{11}{5}=\frac{5}{5}+\frac{5}{5}+\frac{1}{5}[\text { Numerator } 11=5+5+1] $
$=1+1+\frac{1}{5} $
$=2 \frac{1}{5}$
Number of whole units $=2$
$
\frac{9}{4}=\frac{4}{4}+\frac{4}{4}+\frac{1}{4}
$
c) $=1+\frac{1}{4}[$ Numerator $9=4+4+1]$
$
=2 \frac{1}{4}
$
Number of whole units $=2$
Question 2: Can all fractions greater than 1 be written as mixed numbers?
Answer: Yes, all fractions greater than 1 can be written as mixed fractions/numbers.
Question 3: Write the following fractions as mixed fractions (e.g., $\frac{9}{2}=4 \frac{1}{2}$ ):
a. $\frac{9}{2}$
b. $\frac{9}{5}$
C. $\frac{21}{19}$
d. $\frac{47}{9}$
e. $\frac{12}{11}$
f. $\frac{19}{6}$
Answer:
(a)
$\frac{9}{2}=\frac{2}{2}+\frac{2}{2}+\frac{2}{2}+\frac{2}{2}+\frac{1}{2} $
$=1+1+1+1+\frac{1}{2} $
$=4 \frac{1}{2}$
(b)
$\frac{9}{5}=\frac{5}{5}+\frac{4}{5}$
$=1+\frac{4}{5} \\$
$=1 \frac{4}{5}$
(c)
$\frac{21}{19} $
$ =\frac{19}{19}+\frac{2}{19}$
$ =1+\frac{2}{19} \\$
$ =1 \frac{2}{19}$
(d)
$
\frac{47}{9}=\frac{9}{9}+\frac{9}{9}+\frac{9}{9}+\frac{9}{9}+\frac{9}{9}+\frac{2}{9} $
$=1+1+1+1+1+\frac{2}{9} \\$
$=5+\frac{2}{9} \\$
$=5 \frac{2}{9}$
(e)
$
\frac{12}{11} $
$ =\frac{11}{11}+\frac{1}{11} $
$ =1+\frac{1}{11} \\$
$ =1 \frac{1}{11}$
(f)
$
\frac{19}{6}$
$=\frac{6}{6}+\frac{6}{6}+\frac{6}{6}+\frac{1}{6} \\$
$=1+1+1+\frac{1}{6} \\$
$=3+\frac{1}{6} \\$
$=3 \frac{1}{6}$
|
Fractions Class 6 Question Answers |
Question 1: Write the following mixed numbers as fractions:
a. $3 \frac{1}{4}$
b. $7 \frac{2}{3}$
c. $9 \frac{4}{9}$
d. $3 \frac{1}{6}$
e. $2 \frac{3}{11}$
f. $3 \frac{9}{10}$
Answer:
a) Here $3 \frac{1}{4}=3+\frac{1}{4}$
$
\begin{gathered}
=1+1+1+\frac{1}{4} \\
=\frac{4}{4}+\frac{4}{4}+\frac{4}{4}+\frac{1}{4}=\frac{13}{4}
\end{gathered}
$
b) Here $7 \frac{2}{3}=7+\frac{2}{3}$
$
\begin{gathered}
=1+1+1+1+1+1+1+\frac{2}{3} \\
=\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{2}{3} \\
=\frac{23}{3}
\end{gathered}
$
c) Here $9 \frac{4}{9}=9+\frac{4}{9}$
$
\begin{aligned}
& =9 \operatorname{times} \frac{9}{9}+\frac{4}{9} \\
& =\frac{81}{9}+\frac{4}{9}=\frac{85}{9}
\end{aligned}
$
d) Here $3 \frac{1}{6}=3+\frac{1}{6}$
$
\begin{gathered}
=3 \operatorname{times} \frac{6}{6}+\frac{1}{6} \\
=\frac{18}{6}+\frac{1}{6} \\
=\frac{19}{6}
\end{gathered}
$
e) We have $2 \frac{3}{11}=2+\frac{3}{11}$
$
\begin{gathered}
=2 \operatorname{times} \frac{11}{11}+\frac{3}{11} \\
=\frac{22}{11}+\frac{3}{11} \\
=\frac{25}{11}
\end{gathered}
$
(f)
$\begin{aligned} & 3 \frac{9}{10}=3+\frac{9}{10} \\ & \quad=3 \operatorname{times} \frac{10}{10}+\frac{9}{10} \\ & \quad=\frac{30}{10}+\frac{9}{10}=\frac{39}{10}\end{aligned}$
|
Fractions Class 6 Question Answers |
Question 1: Are $\frac{3}{6}, \frac{4}{8}, \frac{5}{10}$ equivalent fractions? Why?
Answer: Here, simplest form of $\frac{3}{6}=\frac{3 \div 3}{6 \div 3}=\frac{1}{2}$ [HCF of 3 and 6 is 3 ]
Simplest form of $\frac{4}{8}$ is $\frac{4 \div 4}{8 \div 4}=\frac{1}{2}$ [HCF of 4 and 8 is 4 ]
Simplest form of $\frac{5}{10}$ is $\frac{5 \div 5}{10 \div 5}=\frac{1}{2}$ [HCF of 5 and 10 is 5] Hence, $\frac{3}{6}, \frac{4}{8}, \frac{5}{10}$ are equivalent fractions.
Question 2: Write two equivalent fractions for $\frac{2}{6}$.
Answer: Here it is given $\frac{2}{6} \rightarrow \frac{2 \times 2}{6 \times 2}, \frac{2 \times 3}{6 \times 3}, \frac{2 \times 4}{6 \times 4}$
Hence $\frac{4}{12}, \frac{6}{18}, \frac{8}{24}$ are equivalent fractions of $\frac{2}{6}$.
Question 3: $\frac{4}{6}=\square-\square=\square=\quad$ (Write as many as you can)
Answer:
$
\begin{gathered}
\frac{4}{6}=\frac{4 \times 2}{6 \times 2}=\frac{4 \times 3}{6 \times 3}=\frac{4 \times 4}{6 \times 4} \\
=\frac{8}{12}=\frac{12}{18}=\frac{16}{24}
\end{gathered}$
|
Fractions Class 6 Question Answers |
Question 1: Three rotis are shared equally by four children. Show the division in the picture and write a fraction for how much each child gets. Also, write the corresponding division facts, addition facts, and multiplication facts.
The fraction of roti each child gets is________.
Division fact:
Additional fact:
Multiplication fact:
Compare your picture and answers with your classmates!
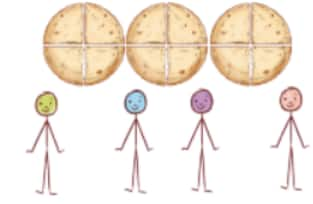
Answer:
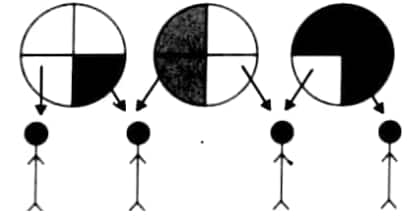
Division fact:
3 wholes divided into 4 parts
$
3 \div 4=\frac{3}{4}
$
Addition fact:
Four times $\frac{3}{4}$ added gives 3 wholes
$
\begin{gathered}
=\frac{3}{4}+\frac{3}{4}+\frac{3}{4}+\frac{3}{4} \\
=\frac{12}{4}=3
\end{gathered}
$
Multiplication fact:
4 parts of $\frac{3}{4}$ make 3 wholes
$
4 \times \frac{3}{4}=3
$
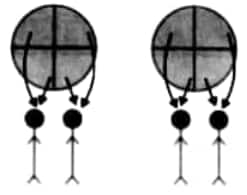
Question 2: Draw a picture to show how much each child gets when 2 rotis are shared equally by 4 children. Also, write the corresponding division facts, addition facts, and multiplication facts.
Answer:
As 2 rotis have to be shared equally by 4 children, we divide each roti into 4 parts and give
(a) 1 part of each roti to each child as shown below:
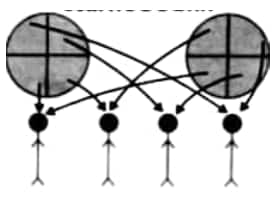
(b) 2 parts to each child as shown below
Question 3: Anil was in a group where 2 cakes were divided equally among 5 children. How much cake would Anil get?
Answer: Anil is in a group where 2 cakes were divided equally among 5 children.

Each cake gets divided into 5 parts, and Anil gets one part from each cake, i.e., $\frac{1}{5}+\frac{1}{5}=\frac{2}{5}$ of a cake.
|
Fractions Class 6 Question Answers |
Question: Find the missing numbers:
a) 5 glasses of juice shared equally among 4 friends is the same as _____ glasses of juice shared equally among 8 friends.
Answer: $\frac{\text { number of glasses }}{\text { number of friends }}=\frac{5}{4}$
Now to determine how many glasses of juice would be needed to give each of the 8 friends the same amount $=8 \times \frac{5}{4}$ $=10$ glasses
So, 10 glasses of juice shared equally among 8 friends is the same as 5 glasses of juice shared equally among 4 friends.
$
\therefore \frac{5}{4}=\frac{10}{8}
$
b) Find the missing numbers: 4 kg of potatoes divided equally in 3 bags is the same as 12 kg of potatoes divided equally in _______ bags.
Answer: Let x be the number of bags for 12 kg of potatoes, where each bag has the same amount of potatoes, then
$
\begin{gathered}
\frac{12 \mathrm{~kg}}{x \text { bags }}=\frac{4}{3} \text { kg per bag } \\
\Rightarrow 12 \times 3=4 \times \mathrm{x} \\
\Rightarrow 36=4 \mathrm{x} \\
\Rightarrow \mathrm{x}=\frac{36}{4} \\
\Rightarrow \mathrm{x}=9 \\
\therefore \frac{4}{3}=\frac{12}{9}
\end{gathered}
$
c) Find the missing numbers: 7 rotis divided among 5 children is the same as _______ rotis divided among ________ children.
Answer: Dividing 7 rotis among 4 children gives 7 rotis each child $=\frac{7}{5}$ of a roti. We can find an equivalent fraction by multiplying both the numerator and the denominator by the same number. For example, multiplying both by 2.
$
\frac{7 \times 2}{5 \times 2}=\frac{14}{10}
$
So, 7 rotis divided among 5 children is the same as 14 rotis divided among 10 children.
$
\therefore \frac{7}{5}=\frac{14}{10}
$
|
Fractions Class 6 Question Answers |
Question: Express the following fractions in their lowest terms:
a. $\frac{17}{51}$
b. $\frac{64}{144}$
C. $\frac{126}{147}$
d. $\frac{525}{112}$
Answer:
a) $\frac{17}{51}=\frac{17}{17 \times 3}=\frac{1}{3}$
b)
$
\begin{aligned}
\frac{64}{144}= & \frac{64 \div 16}{144 \div 16} \\
& =\frac{4}{9}
\end{aligned}
$
c) Here, $\frac{126}{147}$
$
=\frac{126 \div 7}{147 \div 7}
$
[ $\because$ HCF of 126 and 147 is $7 \times 3=21$ ]
$
\begin{aligned}
& =\frac{18 \div 3}{21 \div 3} \\
& =\frac{6}{7}
\end{aligned}
$
d) Here, 525 and 112 are both multiples of 7; we divide both by 7.
$
\begin{aligned}
& =\frac{525 \div 7}{112 \div 7} \\
& =\frac{75}{16}
\end{aligned}
$
|
Fractions Class 6 Question Answers |
Question 1: Compare the following fractions and justify your answers:
a. $\frac{8}{3}, \frac{5}{2}$
b. $\frac{4}{9}, \frac{3}{7}$
c. $\frac{7}{10}, \frac{9}{14}$
d. $\frac{12}{5}, \frac{8}{5}$
e. $\frac{9}{4}, \frac{5}{2}$
Answer:
a. Given fractions are $\frac{8}{3}$ and $\frac{5}{2}$.
Here, the LCM of the denominators 3 and 2 is 6.
Then, multiplying and dividing $\frac{8}{3}$ by 2 and $\frac{5}{2}$ by 3 , then
$
\begin{gathered}
\frac{8 \times 2}{3 \times 2}=\frac{16}{6} \quad, \quad \frac{5 \times 3}{2 \times 3}=\frac{15}{6} \\
\text { Hence, } \frac{16}{6} \quad \frac{15}{6} \\
\Rightarrow \quad \frac{16}{6}>\frac{15}{6} \\
\therefore \quad \frac{8}{3}>\frac{5}{2}
\end{gathered}
$
b. Given fractions are $\frac{4}{9}$ and $\frac{3}{7}$.
Here, the LCM of the denominators 9 and 7 is 63.
then multiplying and dividing $\frac{4}{9}$ by 7 and $\frac{3}{7}$ by 9,
then
Here, $\frac{4 \times 7}{9 \times 7}=\frac{28}{63}$
$
\begin{aligned}
\frac{3 \times 9}{7 \times 9}= & \frac{27}{63} \\
\because & \frac{28}{63}>\frac{27}{63} \\
\therefore \frac{4}{9} & >\frac{3}{7}
\end{aligned}
$
c. Given fractions are $\frac{7}{10}$ and $\frac{9}{14}$.
Here, the LCM of the denominators 10 and 14 is 70.
then multiplying and dividing $\frac{7}{10}$ by 7 and $\frac{9}{14}$ by 5,
then
$
\begin{aligned}
& \frac{7 \times 7}{10 \times 7}=\frac{49}{70}, \frac{9 \times 5}{14 \times 5}=\frac{45}{70} \\
& \frac{49}{70}>\frac{45}{70} \\
& \frac{7}{10}>\frac{9}{14}
\end{aligned}
$
d. Given fractions are $\frac{12}{5}, \frac{8}{5}$.
Here, denominator is same so $\frac{12}{5}>\frac{8}{5}$
e. Given fractions are $\frac{9}{4}, \frac{5}{2}$.
Here, the LCM of the denominators 4 and 2 is 4. Then, multiplying and dividing $\frac{5}{2}$ by 2 and Equivalent fractions with 4 are $\frac{5 \times 2}{2 \times 2}$
$
\begin{aligned}
& \frac{10}{4}>\frac{9}{4} \\
& \therefore \frac{5}{2}>\frac{9}{4}
\end{aligned}
$
Question 2: Write the following fractions in ascending order.
a. $\frac{7}{10}, \frac{11}{15}, \frac{2}{5}$
b. $\frac{19}{24}, \frac{5}{6}, \frac{7}{12}$
Answer:
a)
LCM of 10,15 and $5=2 \times 3 \times 5=30$
Now, let us make the denominator of each fraction as LCM
$
\begin{aligned}
& \frac{7 \times 3}{10 \times 3}, \frac{11 \times 2}{15 \times 2}, \frac{2 \times 6}{5 \times 6} \\
& \frac{21}{30}, \frac{22}{30}, \frac{12}{30}
\end{aligned}
$
Clearly $\frac{12}{30}<\frac{21}{30}<\frac{22}{30}$
$
\Rightarrow \frac{2}{5}<\frac{7}{10}<\frac{11}{5}
$
b) The given fractions are $\frac{19}{24}, \frac{5}{6}, \frac{7}{12}$
Here LCM of $24,6,12$ is 24.
$
\therefore \frac{19 \times 1}{24 \times 1}, \frac{5 \times 4}{6 \times 4}, \frac{7 \times 2}{12 \times 2}
$
Thus $\frac{19}{24}<\frac{20}{24}>\frac{14}{24}$
On arranging in ascending Order, we get
$
\begin{aligned}
& \frac{14}{24}, \frac{19}{24}, \frac{20}{24} \\
& \Rightarrow \frac{7}{12}, \frac{19}{24}, \frac{5}{6}
\end{aligned}
$
Question 3: Write the following fractions in descending order.
a. $\frac{25}{16}, \frac{7}{8}, \frac{13}{4}, \frac{17}{32}$
b. $\frac{3}{4}, \frac{12}{5}, \frac{7}{12}, \frac{5}{4}$
Answer:
a) LCM of $16,8,4,32=2 \times 2 \times 2 \times 2 \times 2=32$
Now, let us make the denominator of each fraction the LCM, thus
$
\begin{gathered}
\therefore \frac{25 \times 2}{16 \times 2}, \frac{7 \times 4}{8 \times 4}, \frac{13 \times 8}{4 \times 8}, \frac{17 \times 1}{32 \times 1} \\
=\frac{50}{32}, \frac{28}{32}, \frac{104}{32}, \frac{17}{32}
\end{gathered}
$
On arranging in descending order, we get
$
\begin{gathered}
\frac{104}{32}>\frac{50}{32}>\frac{28}{32}>\frac{17}{32} \\
\therefore \frac{13}{4}>\frac{25}{16}>\frac{7}{8}>\frac{17}{32}
\end{gathered}
$
Hence, given fractions in descending order are $\frac{13}{4}, \frac{25}{16}, \frac{7}{8}$ and $\frac{17}{32}$
b) Here LCM of $4,5,12,4$ is 60.
Now, let us make the denominator of each fraction the LCM, then
$
\begin{gathered}
\frac{3 \times 15}{4 \times 15}, \frac{12 \times 12}{5 \times 12}, \frac{7 \times 5}{12 \times 5}, \frac{5 \times 15}{4 \times 15} \\
=\frac{45}{60}, \frac{144}{60}, \frac{35}{60}, \frac{75}{60} \\
\frac{144}{60}>\frac{75}{60}>\frac{45}{60}>\frac{35}{60}
\end{gathered}
$
Hence, fractions in descending order are
$
\frac{12}{5}>\frac{5}{4}>\frac{3}{4}>\frac{7}{12}
$
|
Fractions Class 6 Chapter 7 Question Answers |
Question 1: Add the following fractions using Brahmagupta's method:
a. $\frac{2}{7}+\frac{5}{7}+\frac{6}{7}$
b. $\frac{3}{4}+\frac{1}{3}$
c. $\frac{2}{3}+\frac{5}{6}$
d. $\frac{2}{3}+\frac{2}{7}$
e. $\frac{3}{4}+\frac{1}{3}+\frac{1}{5}$
f. $\frac{2}{3}+\frac{4}{5}$
g. $\frac{4}{5}+\frac{2}{3}$
h. $\frac{3}{5}+\frac{5}{8}$
i. $\frac{9}{2}+\frac{5}{4}$
j. $\frac{8}{3}+\frac{2}{7}$
k. $\frac{3}{4}+\frac{1}{3}+\frac{1}{5}$
l. $\frac{2}{3}+\frac{4}{5}+\frac{3}{7}$
m. $\frac{9}{2}+\frac{5}{4}+\frac{7}{6}$
Answer:
(a)
Given: $\frac{2+5+6}{7}$
$=\frac{13}{7} $
$ =\frac{7+6}{7} $
$=\frac{7}{7}+\frac{6}{7} $
$ = 1+\frac{6}{7}$
$=1 \frac{6}{7} $
(b)
Here $\frac{3}{4}+\frac{1}{3}$
Here, the LCM of the denominators 4 and 3 is 12
$\therefore$ Equivalent fraction of $\frac{3}{4}$ with denominators 12 is $\frac{9}{12}$ and equivalent fraction of $\frac{1}{3}$ with denominators 12 is $\frac{4}{12}$
Hence,
$ \frac{9}{12}+\frac{4}{12} \\$
$= \frac{9+4}{12}=\frac{13}{12} \\$
$= \frac{12+1}{12}$
$=1+\frac{1}{12} \\$
$= 1 \frac{1}{12}$
(c)
$\begin{aligned} & \frac{2}{3}+\frac{5}{6}= \frac{2 \times 2}{3 \times 2}+\frac{5 \times 1}{6 \times 1} \\ &= \frac{4}{6}+\frac{5}{6} \\ &=\frac{9}{6} \\ &= \frac{6+3}{6} \\ &= 1+\frac{3}{6} \\ &= 1+\frac{1}{2} \quad\left[\text { Bring to lowest term } \frac{3}{6}\right] \\ &=1 \frac{1}{2}\end{aligned}$
(d)
Expressing as equivalent fractions with denominators 21, we get
$
\begin{array}{ll}
& \frac{2 \times 7}{3 \times 7}+\frac{3 \times 3}{7 \times 3} \\
= & \frac{14}{21}+\frac{9}{21} \\
= & \frac{23}{21} \\
= & \frac{21}{21}+\frac{2}{21}=1+\frac{2}{21}=1 \frac{2}{21}
\end{array}
$
(e)
$\begin{array}{ll} & \frac{3 \times 15}{4 \times 15}+\frac{1 \times 20}{3 \times 20}+\frac{1 \times 12}{5 \times 12} \\ = & \frac{45}{60}+\frac{20}{60}+\frac{12}{60} \\ = & \frac{45+20+12}{60} \\ = & \frac{77}{60} \\ = & \frac{60+17}{60} \\ = & 1 \frac{17}{60}\end{array}$
(f)
Expressed as equivalent fractions with denominators 15, we get
$\frac{2 \times 5}{3 \times 5}+\frac{4 \times 3}{5 \times 3} \\$
$=\frac{10}{15}+\frac{12}{15} \\$
$=\frac{22}{15} \\$
$=\frac{15+7}{15} \\$
$=\frac{15}{15}+\frac{7}{15} $
$=1+\frac{7}{15} \\$
$=1 \frac{7}{15}$
(g)
$\frac{4 \times 3}{5 \times 3}+\frac{2 \times 5}{3 \times 5} \\$
$ =\frac{12}{15}+\frac{10}{15} \\$
$ =\frac{12+10}{15} $
$ =\frac{22}{15} $
$=\frac{15}{15}+\frac{7}{15} $
$=1+\frac{7}{15} $
$=1 \frac{7}{15}$
(h)
$\frac{3 \times 8}{5 \times 8}+\frac{5 \times 5}{8 \times 5} \\$
$ =\frac{24}{40}+\frac{25}{40} \\ $
$=\frac{24+25}{40} \\ $
$=\frac{49}{40} \\ $
$=\frac{40}{40}+\frac{9}{40} \\ $
$=1+\frac{9}{40} \\ $
$=1 \frac{9}{40}$
(i)
$\begin{aligned} & \frac{9 \times 2}{2 \times 2}+\frac{5 \times 1}{4 \times 1} \\ &=\frac{18}{4}+\frac{5}{4} \\ &=\frac{18+5}{4} \\ &=\frac{23}{4} \\ &=\frac{20+3}{4} \\ &=\frac{20}{4}+\frac{3}{4} \\ &=\frac{5 \times 4+3}{4} \\ &= 5 \frac{3}{4}\end{aligned}$
(j)
Expressing as equivalent fractions with denominators 21(LCM), we get
$\frac{8 \times 7}{3 \times 7}+\frac{2 \times 3}{7 \times 3} \\$
$=\frac{56}{21}+\frac{6}{21} \\$
$=\frac{62}{21} \\$
$=\frac{42+20}{21} \\$
$=\frac{21 \times 2}{21}+\frac{20}{21} \\$
$=\frac{21 \times 2}{21}+\frac{20}{21} \\$
$=2+\frac{20}{21}$
$=2 \frac{20}{21}$
(k)
Expressing as equivalent fractions with denominators $60(\mathrm{LCM})$, we get
$=\frac{3 \times 15}{4 \times 15}+\frac{1 \times 20}{3 \times 20}+\frac{1 \times 12}{5 \times 12} \\$
$=\frac{45}{60}+\frac{20}{60}+\frac{12}{60} \\$
$=\frac{45+20+12}{60} \\$
$=\frac{77}{60} \\$
$=\frac{60+17}{60} \\$
$=\frac{60}{60}+\frac{17}{60} \\$
$=1+\frac{17}{60} \\$
$=1 \frac{17}{60}$
(l)
I) Expressing as equivalent fractions with denominators 105(LCM), we get
$
\frac{2 \times 35}{3 \times 35}+\frac{4 \times 21}{5 \times 21}+\frac{3 \times 15}{7 \times 15} \\$
$=\frac{70}{105}+\frac{84}{105}+\frac{45}{105} \\$
$=\frac{70+84+45}{105} \\$
$=\frac{199}{105} \\$
$=\frac{105+94}{105} \\$
$=\frac{105}{105}+\frac{94}{105} \\$
$=1 \frac{94}{105}$
(m)
Expressing as equivalent fractions with denominators 12(LCM), we get
$
\frac{9 \times 6}{2 \times 6}+\frac{5 \times 3}{4 \times 3}+\frac{7 \times 2}{6 \times 2} \\$
$=\frac{54}{12}+\frac{15}{12}+\frac{14}{12} \\$
$=\frac{54+15+14}{12}=\frac{83}{12} \\$
$=\frac{12+12+12+12+12+12+11}{12} \\$
$=\frac{12 \times 6+11}{12} \\$
$=\frac{12 \times 6}{12}+\frac{11}{12} \\$
$=6 \frac{11}{12}$
Question 2: Rahim mixes $\frac{2}{3}$ litres of yellow paint with $\frac{3}{4}$ litres of blue paint to make green paint. What is the volume of green paint he has made?
Answer:
Given quantity of yellow paint $=\frac{2}{3}$ litres
and quality of blue paint $=\frac{3}{4}$ litres
Volume of green paint made
$
=\frac{2}{3} \text { litres }+\frac{3}{4} \text { litres }
$
Here LCM of 3 and 4 is 12.
Now expressed as equivalent fractions with a denominator of 12, we get
$
\begin{aligned}
& \frac{2 \times 4}{3 \times 4}+\frac{3 \times 3}{4 \times 3} \\
& =\frac{8+9}{12} \\
& =\frac{17}{12} \\
& =\frac{12+5}{12} \\
& =\frac{12}{12}+\frac{5}{12} \text { litres } \\
& =1 \frac{5}{12} \text { litres }
\end{aligned}
$
Question 3: Geeta bought $\frac{2}{5}$ meter of lace, and Shamim bought $\frac{3}{4}$ meter of the same lace to put a complete border on a tablecloth whose perimeter is 1 meter long. Find the total length of the lace they have both bought. Will the lace be sufficient to cover the whole border?
Answer:
Given length of lace bought by Geeta $=\frac{2}{5}$ meter
and length of lace bought by Shamim $=\frac{3}{4}$ metre
Total length of lace $=\frac{2}{5}+\frac{3}{4}$ metre
LCM of 5 and 4 is 20
Now expressed as equivalent fractions with a denominator of 20, we get,
$
\begin{gathered}
=\frac{2 \times 4}{5 \times 4}+\frac{3 \times 5}{4 \times 5} \\
=\frac{8+15}{20} \\
=\frac{23}{20} \\
=\frac{20}{20}+\frac{3}{20} \\
=1+\frac{3}{20} \mathrm{~m}
\end{gathered}
$
Total lace required $=$ Perimeter $=1 \mathrm{~m}$
Hence, the total lace Geeta and Shamim have together is sufficient to cover the whole border.
|
Fractions Class 6 Chapter 7 Question Answers |
Question 1: $\frac{5}{8}-\frac{3}{8}$
Answer:
As fractional unit is same i.e., $\frac{1}{8}$ we shall simply subtract numerators keeping fractional unit as $\frac{1}{8}$
Then $\frac{5}{8}-\frac{3}{8}=\frac{5-3}{8}=\frac{2}{8}=\frac{1}{4}$ (representing in simplest form)
Question 2: $\frac{7}{9}-\frac{5}{9}$
Answer:
As fractional unit is same i.e., $\frac{1}{9}$ we shall simply subtract numerators keeping fractional unit as $\frac{1}{9}$
$
\begin{aligned}
& \frac{7}{9}-\frac{5}{9} \\
= & \frac{7-5}{9}=\frac{2}{9}
\end{aligned}
$
Question 3:
$\frac{10}{27}-\frac{1}{27}$
Answer: Here $\frac{10}{27}-\frac{1}{27}$
$
\begin{aligned}
& =\frac{10-1}{27} \\
& =\frac{9}{27}=\frac{1}{3}
\end{aligned}
$
|
Fractions Class 6 Chapter 7 Question Answers |
Question 1: Carry out the following subtractions using Brahmagupta's method:
a. $\frac{8}{15}-\frac{3}{15}$
b. $\frac{2}{5}-\frac{4}{15}$
c. $\frac{5}{6}-\frac{4}{9}$
d. $\frac{2}{3}-\frac{1}{2}$
Answer:
a) Given $\frac{8}{15}-\frac{3}{15}$
Fractional unit for both fractions is $\frac{1}{15}$ then
$
\begin{aligned}
\frac{8}{15}-\frac{3}{15} & =\frac{8-3}{15} \\
=\frac{5}{15} & =\frac{1}{3}
\end{aligned}
$
b) Given $\frac{2}{5}-\frac{4}{15}$
Here LCM of 5 and 15 is 15. Fractional unit for both fractions should be $\frac{1}{15}$ then
$
\begin{aligned}
& \frac{2}{5}-\frac{4}{15} \\
& =\frac{2 \times 3}{5 \times 3}-\frac{4 \times 1}{15 \times 1} \\
& =\frac{6}{15}-\frac{4}{15} \\
& =\frac{6-4}{15} \\
& =\frac{2}{15}
\end{aligned}
$
c) Given $\frac{5}{6}-\frac{4}{9}$
Hence LCM of 6 and 9 is 18. Fractional unit for both fractions should be $\frac{1}{18}$ then
Given $\frac{5}{6}-\frac{4}{9}$
$
\begin{aligned}
& =\frac{5 \times 3}{6 \times 3}-\frac{4 \times 2}{9 \times 2} \\
& =\frac{15}{18}-\frac{8}{18} \\
& =\frac{15-8}{18} \\
& =\frac{7}{18}
\end{aligned}
$
d) Given $\frac{2}{3}-\frac{1}{2}$
Here, the LCM of 3 and 2 is 6. Fractional unit for both fractions should be $\frac{1}{6}$
So, $\frac{2}{3}-\frac{1}{2}$
$
\begin{aligned}
& =\frac{2 \times 2}{3 \times 2}-\frac{1 \times 3}{2 \times 3} \\
& =\frac{4}{6}-\frac{3}{6} \\
& =\frac{4-3}{6} \\
& =\frac{1}{6}
\end{aligned}
$
Question 2: Subtract as indicated:
a. $\frac{13}{4}$ from $\frac{10}{3}$
b. $\frac{18}{5}$ from $\frac{23}{3}$
C. $\frac{29}{7}$ from $\frac{45}{7}$
Answer:
(a)
$\frac{10}{3}-\frac{13}4$
$=\frac{10 \times 4}{3 \times 4}-\frac{13 \times 3}{4 \times 3} $
$= \frac{40}{12}-\frac{39}{12} $
$= \frac{40-39}{12} $
$ =\frac{1}{12} $
(b)
$\frac{23}{3}-\frac{18}{5}$
$=\frac{23 \times 5}{3 \times 5}-\frac{18 \times 3}{5 \times 3}$
$=\frac{115}{15}-\frac{54}{15}$
$= \frac{115-54}{15} $
$=\frac{61}{15} $
$=4 \frac{1}{15}$
(c)
$\frac{45}{7}-\frac{29}{7}$
$\begin{aligned} &= \frac{45}{7}-\frac{29}{7} \\ &= \frac{45-29}{7} \\ &= \frac{16}{7} \\ &= \frac{7 \times 2+2}{7} \\ &= \frac{7 \times 2}{7}+\frac{2}{7} \\ &= 2+\frac{2}{7} \\ &= 2 \frac{2}{7}\end{aligned}$
Question 3: Solve the following problems:
a. Jaya's school is $\frac{7}{10} \mathrm{~km}$ from her home. She takes an auto for $\frac{1}{2} \mathrm{~km}$ from her home daily, and then walks the remaining distance to reach her school. How much does she walk daily to reach the school?
b. Jeevika takes $\frac{10}{3}$ minutes to take a complete round of the park, and her friend Namit takes $\frac{13}{4}$ minutes to do the same. Who takes less time, and by how much?
Answer:
a) Given the distance between Jaya's school and home is $\frac{7}{10} \mathrm{~km}$ and the distance covered by Jaya in the auto is $\frac{1}{2} \mathrm{~km}$.
$\therefore$ Distance Jaya covered by walking $=\frac{7}{10} \mathrm{~km}-\frac{1}{2} \mathrm{~km}$
LCM of 10 and 2 is 10.
$
\begin{gathered}
=\left[\frac{7}{10}-\frac{1 \times 5}{2 \times 5}\right] \mathrm{km} \\
=\left[\frac{7-5}{10}\right] \mathrm{km} \\
=\frac{2}{10} \mathrm{~km} \\
=\frac{1}{5} \mathrm{~km}(\text { lowest form })
\end{gathered}
$
b) Time taken by Jeevika to cover 1 round of the park $=\frac{10}{3} \mathrm{~mm}$ Time taken by Namit to cover 1 round of the 13 park $=\frac{13}{4} \mathrm{~min}$
To find who takes less time we need to compare $\frac{10}{3}$ and $\frac{13}{4}$ Here, LCM of 3 and 4 is 12 .
So, the time taken by Jevika and Namit will be $\frac{10 \times 4}{3 \times 4}=\frac{40}{12}$ minutes and $\frac{13 \times 3}{4 \times 3}=\frac{39}{12}$ minutes, respectively.
Clearly $\frac{40}{12}>\frac{39}{12}$
Hence, Namit takes less time by $\frac{40}{12}-\frac{39}{12}=\frac{40-39}{12}=\frac{1}{12}$ minutes.
NCERT Fractions Class 6 Maths Chapter 7 - Topics
Topics you will learn in NCERT Class 6 Maths Chapter 7 Fractions include:
7.1 Fractional Units and Equal Shares
7.2 Fractional Units as Parts of a Whole
7.3 Measuring Using Fractional Units
7.4 Marking Fraction Lengths on the Number Line
7.5 Mixed Fractions
7.6 Equivalent Fractions
7.7 Simplest form of a Fraction
7.8 Comparing Fractions
7.9 Relation to Number Sequences
Class 6 Maths Chapter 7 Fractions solutions: Extra Question
Question:
Kushal has a chocolate bar, and he wants to share it equally with her 3 friends. If the chocolate bar is divided into 4 equal parts, what fraction of the chocolate bar will each person get?
Solution:
The chocolate bar is divided into 4 equal parts.
Kushal and his 3 friends, so there are 4 people in total.
Since the chocolate bar is divided into 4 equal parts, and 4 people will share it, each person gets $\frac{1}{4}$ of the chocolate bar.
Hence, each person will get $\frac{1}{4}$ of the chocolate bar.
NCERT Solutions for Class 6 Maths Chapter 7 Fractions: Notes
Careers360 has prepared these Class 6 Fractions Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Fractions NCERT solutions and solve them independently from next time.
Fractions
Fractions can be defined as a part of a whole. When one unit is divided into several equal parts, each part is called a fractional unit. The fractional units are $\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \ldots, \frac{1}{10}, \ldots, \frac{1}{50}, \ldots, \frac{1}{100}$, etc. We also sometimes refer to fractional units as unit fractions.
We usually read the fraction $\frac{3}{4}$ as 'three quarters' or 'three upon four', but reading it as ' 3 times $\frac{1}{4}$ ', helps us to understand the size of the fraction because it shows what the fractional unit is $\left(\frac{1}{4}\right)$ and how many such fractional units (3) there are.
Fraction on Number Line
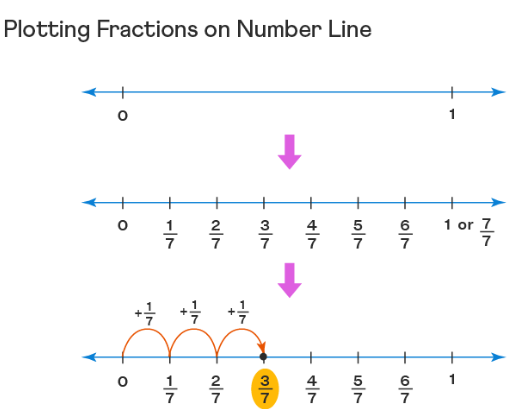
We can easily mark fractions on a number line. Here we mark numbers as 0 and 1 and divide them into 7 equal parts. So, starting from $\frac{1}{7}, \frac{2}{7}$ and till we write 1 as $\frac{7}{7}$.
Mixed Fractions
These fractions are represented as a mix of 3 numbers instead of 2. They are improper fractions in which the numerator is bigger than the denominator, unlike the normal ones.
For example,
$\frac{3}{2}=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+\frac{1}{2}$
$
\frac{5}{2}=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=2+\frac{1}{2}
$
Equivalent Fractions
'Equivalent fractions' are those that denote the same length, but they are expressed in terms of different fractional units. For eg, $\frac{1}{2}, \frac{2}{4}$, etc.
Addition and Subtraction of Fractions
Fractions can be added and subtracted provided their denominator are the same. If not, we take the LCM to make the denominators the same and then perform operations.
For example:
$\frac{3}{8}+\frac{7}{8}=\frac{3+7}{8}=\frac{10}{8}$
In the above case, the denominator is the same, so we have directly added the numerators. We must remember that neither in addition nor subtraction is the denominator added or subtracted.
Example:
$\frac{2}{5}+\frac{1}{3}=\frac{2 \times 3}{5 \times 3}+\frac{1 \times 5}{3 \times 5}=\frac{6}{15}+\frac{5}{15}=\frac{11}{15} $
$\frac{1}{2}+\frac{1}{3}=\frac{1 \times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2}=\frac{3}{6}+\frac{2}{6}=\frac{5}{6}$
In the above example, we notice that the denominators of both fractions are not the same. Hence, we take the LCM first and then multiply the numerator and denominator by the desired factor to finally add them.
Subtraction of Fractions:
$
\frac{7}{6}-\frac{3}{6}=\frac{4}{6}
$
In the above case, the denominator is the same, so we have directly subtracted the numerators.
If the denominators of both fractions are not the same. We take the LCM first and then multiply the numerator and denominator by the desired factor to finally subtract them.
NCERT Solutions for Class 6 Maths Chapter 7 Fractions - Points to Remember
Check the following important points to understand and solve the Fractions Class 6 question answers effectively.
Fractions: Fractions are numbers that are used to represent a part of the whole. For example, $\frac{1}{2}$ is a fraction representing half of the whole.
Improper fractions: Improper fractions are fractions in which the numerator is greater than the denominator. Eg. $\frac{7}{2}$
Mixed fractions: Mixed fractions are another form of improper fractions in the form $a \frac{b}{c}$ where $\frac{b}{c}$ is a proper fraction. Eg. $3 \frac{1}{2}$
Equivalent Fractions: Equivalent fractions are fractions with the same value but different representations. Example: $\frac{1}{2}=\frac{3}{6}=\frac{4}{8}$
Addition or Subtraction of Fractions: Addition and subtraction of fractions are possible only when the denominators are the same. For example, $\frac{1}{5}+\frac{3}{5}=\frac{4}{5}$
If the denominators of the fractions to be added or subtracted are different, the LCM should be taken to make the denominators the same to add or subtract the fractions.
$\frac{1}{3}+\frac{3}{6} \Rightarrow \frac{2}{6}+\frac{3}{6}=\frac{5}{6}$
Why are Class 6 Maths Chapter 7 Fractions question answers important?
Fractions are one of the most used concepts in the field of mathematics, and are also important to understand some important mathematical concepts, such as decimals, ratios, percentages, and algebra. Here are some more points on why these question answers are important.
- These Class 6 Maths Fractions question answers clear the basic fraction concepts, such as the numerator and denominator.
- Several practice sessions of this chapter help in understanding the fraction operations such as addition, subtraction, multiplication, and division.
- Questions from this chapter often appear in several board exams and math Olympiads.
- These solutions prepare students for higher classes, where they will use fractions extensively.
NCERT Solutions for Class 6 Maths Chapter Wise
We at Careers360 compiled all the NCERT class 6 Maths solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and Syllabus
Students can also check the NCERT Books and the NCERT Syllabus for Class 6 here:
Frequently Asked Questions (FAQs)
We have to make the denominators same and compare the numerators. The fraction with a greater numerator is the larger one.
Questions from this chapter can be of different types, such as simplifying fractions, solving equations, performing fraction operations, and real-life applications.
If the denominators are the same, add/subtract the numerators directly.
If the denominators are different, find the LCM of the denominators, make them the same, then add or subtract.
Yes, NCERT Solutions are sufficient for exams, as most questions are directly based on the textbook. However, practising extra questions can improve problem-solving speed.
Yes, they build a strong foundation in fractions, which is very useful for Olympiad and aptitude-based exams.
A mixed fraction consists of a whole number and a proper fraction combined.
Example: 2 (2/3), 1 (1/3), etc.
NCERT Class 6 Maths Chapter 7 Fractions covers:
- Fractional units and equal shares
- Fractional units as a part of a whole
- Measuring using fractional units
- Marking fractions on number lines
- Mixed fractions
- Equivalent fractions
- Comparing fractions
- Addition and Subtraction of Fractions
Yes, you can download the NCERT Solutions for Class 6 Maths Chapter 7 in PDF format from educational websites such as Careers360. These solutions have been prepared by highly experienced faculty, following the latest NCERT syllabus. You can use the PDF to cross-check your answers and understand different methods of solving complex problems with ease.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters