In this chapter, we learned about integers and how numbers work on both sides of zero using a number line and real-life examples. NCERT Solutions for Class 6 Maths Chapter 10 explain addition, subtraction, comparing integers, and the rules given by Brahmagupta in an easy way. By practising these solutions, students can understand negative numbers better and gain confidence in solving integer problems used in daily life.
Search Colleges, Exams, Schools & more
Login
NCERT Solutions for Class 6 Maths Chapter 10 - The Other Side of Zero
We are surrounded by many different types of numbers, which is why we need to understand how these numbers can act in different contexts. We are mainly familiar with the positive numbers, but in Chapter 10, The Other Side of Zero, we are introduced to the concept of negative numbers. In this chapter, we can learn about the numbers that lie to the left of zero on the number line, which will broaden our horizon beyond the natural numbers and whole numbers. These NCERT Solutions for Class 6 Maths are designed in such a manner that helps students strengthen their conceptual clarity and improve problem-solving and analytical skills.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Download Free PDF
- NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Exercise Questions
- NCERT The Other Side of Zero Class 6 Maths Chapter 10: Topics
- Class 6 Maths Chapter 10 The Other Side of Zero solutions: Extra Questions
- NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Notes
- NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Points to Remember
- Why are Class 6 Maths Chapter 10 The Other Side of Zero question answers important?
- NCERT Solutions for Class 6 Mathematics Chapter Wise
- NCERT Books and NCERT Syllabus
This article contains comprehensive solutions for all the questions in this chapter. These NCERT Solutions for Class 6 provide detailed, step-by-step explanations for students. With the help of these solutions, they can practice the problems, verify their answer and strengthen their weak areas that need improvement. This will also clear their doubts and provide them with a proper understanding of the chapter's concepts. These NCERT Solutions are trustworthy and reliable because they are created by subject-matter experts at Careers360, making them an essential resource for exam preparation. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Download Free PDF
Careers360 brings you Class 6 Maths Chapter 10 The Other Side of Zero question answers, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Exercise Questions
Below are the detailed Class 6 Maths Chapter 10 The Other Side of Zero question answers provided in the textbook.
|
The Other Side of Zero Class 6 Question answers Page number: 243 |
Question 1: What do you press to go four floors up?
Answer: To go four floors up, you must press +4, i.e. the + button 4 times.
Question 2: What do you press to go three floors down?
Answer: To go three floors down, you must press –3, i.e. the – button 3 times.
|
The Other Side of Zero Class 6 Question answers Page number: 244 |
Question: Number all the floors in the Building of Fun.
Answer:
|
Floor Number |
Description |
|
+6 |
Space Centre |
|
+5 |
Sports Centre |
|
+4 |
Ice Cream Shop |
|
+3 |
Book Store |
|
+2 |
Art Centre |
|
+1 |
Food Court |
|
0 |
Welcome Hall |
|
-1 |
Toy Store |
|
-2 |
Video Games Shop |
|
-3 |
Cinema Centre |
|
-4 |
Ghost House |
|
-5 |
Dinosaur Centre |
|
The Other Side of Zero Class 6 Question answers Page number: 245 |
Question: Start from the Food Court and press + 2 in the lift. Where will you reach? ____________
Answer:
You will reach the Book Store.
|
The Other Side of Zero Class 6 Question answers Page number: 245 |
Question 1: You start from Floor +2 and press –3 in the lift. Where will you reach? Write an expression for this movement.
Answer:
You will reach the -1 floor, which is Toy Store.
The expression for this movement is: (+2) + (-3) = (-1)
Question 2: Evaluate these expressions (you may think of them as Starting Floor + Movement by referring to the Building of Fun).
a. (+1) + (+4) = _______
b. (+4) + (+1) = _______
c. (+4) + (–3) = _______
d. (–1) + (+2) = _______
e. (–1) + (+1) = _______
f. 0 + (+2) = _________
g. 0 + (–2) = _________
Answer:
a. (+1) + (+4) = (+5)
b. (+4) + (+1) = (+5)
c. (+4) + (–3) = (+1)
d. (–1) + (+2) = (+1)
e. (–1) + (+1) = 0
f. 0 + (+2) = (+2)
g. 0 + (–2) = (–2)
Question 3: Starting from different floors, find the movements required to reach Floor –5. For example, if I start at Floor +2, I must press –7 to reach Floor –5. The expression is (+2) + (–7) = –5. Find more such starting positions and the movements needed to reach Floor –5 and write the expressions.
Answer:
|
Starting Floor Number |
Movements Required |
Expression |
|
+6 |
(–11) |
(+6) + (–11) = –5 |
|
+5 |
(–10) |
(+5) + (–10) = –5 |
|
+4 |
(–9) |
(+4) + (–9) = –5 |
|
+3 |
(–8) |
(+3) + (–8) = –5 |
|
+2 |
(–7) |
(+2) + (–7) = –5 |
|
+1 |
(–6) |
(+1) + (–6) = –5 |
|
0 |
(–5) |
0 + (–5) = –5 |
|
–1 |
(–4) |
(–1) + (–4) = –5 |
|
–2 |
(–3) |
(–2) + (–3) = –5 |
|
–3 |
(–2) |
(–3) + (–2) = –5 |
|
–4 |
(–1) |
(–4) + (–1) = –5 |
|
–5 |
0 |
(–5) + 0 = –5 |
|
The Other Side of Zero Class 6 Question answers Page number: 246 |
Figure it out
Question 1: Evaluate these expressions by thinking of them as the resulting movement of combining button presses:
a. (+1)+(+4) = __________
b. (+4)+(+1) = _____________
c. (+4)+(– 3)+(–2) = _______
d. (–1)+(+2)+(–3) = _______
Answer:
-
(+1)+(+4) = (+5)
-
(+4)+(+1) = (+5)
-
(+4)+(–3)+(–2) = (–1)
-
(–1)+(+2)+(–3) = (–2)
Question 2: Write the inverses of these numbers: +4, –4, –3, 0, +2, –1.
Answer:
The inverse of (+4) is (–4).
The inverse of (–4) is (+4).
The inverse of (–3) is (+3).
The inverse of (0) is (0).
The inverse of (+2) is (–2).
The inverse of (–1) is (+1).
Question 3: Connect the inverses by drawing lines.
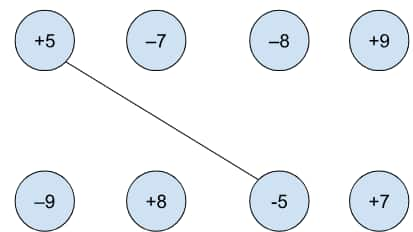
Answer:
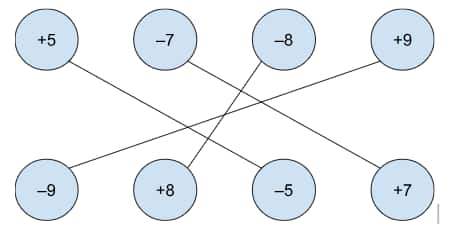
Question 4: Who is on the lowest floor?
-
Jay is in the Art Centre. So, he is on Floor +2.
-
Asin is in the Sports Centre. So, she is on Floor ___.
-
Binnu is in the Cinema Centre. So, she is on Floor ____.
-
Aman is in the Toys Store. So, he is on Floor ____.
Answer:
-
Jay is in the Art Centre. So, he is on Floor +2.
-
Asin is in the Sports Centre. So, she is on Floor (+5).
-
Binnu is in the Cinema Centre. So, she is on Floor (–3).
-
Aman is in the Toys Store. So, he is on Floor (–1).
So, Binnu is on the lowest floor as (–3) is less than (–1).
|
The Other Side of Zero Class 6 Question answers Page number: 247 |
Figure it Out
Question 1: Compare the following numbers using the Building of Fun and fill in the boxes with < or >.
Answer:
Question 2: Imagine the Building of Fun with more floors. Compare the numbers and fill in the boxes with < or >:
Answer:
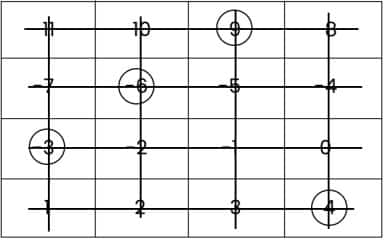
Question 3: If Floor A = –12, Floor D = –1, and Floor E = +1 in the building shown on the right as a line, find the numbers of Floors B, C, F, G, and H.
Answer:
The number of Floor B is (–9).
The number of Floor C is (–6).
The number of Floor F is (+2).
The number of Floor G is (+6).
The number of Floor H is (+11).
Question 4: Mark the following floors of the building shown on the right.
a. –7
b. – 4
c. +3
d. – 10
Answer:
|
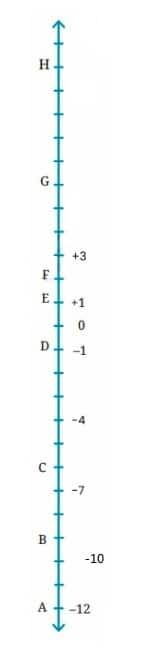
The Other Side of Zero Class 6 Question answers Page number: 248 |
Question 1: Evaluate 15 – 5, 100 – 10, and 74 – 34 from this perspective.
Answer:
15 – 5 = 10
100 – 10 = 90
74 – 34 = 40
|
The Other Side of Zero Class 6 Question answers Page number: 249 |
Figure it Out:
Question 1: Complete these expressions. You may think of them as finding the movement needed to reach the Target Floor from the Starting Floor.
a. (+1) – (+4) = _______
b. (0) – (+2) = _________
c. (+4) – (+1) = _______
d. (0) – (–2) = _________
e. (+4) – (–3) = _______
f. (–4) – (–3) = ________
g. (–1) – (+2) = _______
h. (–2) – (–2) = ________
i. (–1) – (+1) = _______
j. (+3) – (–3) = ________
Answer:
a. (+1) – (+4) = (–3)
b. (0) – (+2) = (–2)
c. (+4) – (+1) = (+3)
d. (0) – (–2) = (+2)
e. (+4) – (–3) = (+7)
f. (–4) – (–3) = (–1)
g. (–1) – (+2) = (–3)
h. (–2) – (–2) = (0)
i. (–1) – (+1) = (–2)
j. (+3) – (–3) = (+6)
|
The Other Side of Zero Class 6 Question answers Page number: 251 |
Figure it Out:
Question 1: Complete these expressions.
a. (+40) + ______ = +200
b. (+40) +_______ = –200
c. (–50) + ______ = +200
d. (–50) +_______ = –200
e. (–200) – (–40) = _______
f. (+200) – (+40) = _______
g. (–200) – (+40) = _______
Answer:
a. (+40) + (+160) = +200
b. (+40) + (–240) = –200
c. (–50) + (+250) = +200
d. (–50) + (–150) = –200
e. (–200) – (–40) = –160
f. (+200) – (+40) = +160
g. (–200) – (+40) = –240
Question 2:
Try evaluating the following expressions by similarly drawing or imagining a suitable lift:
a. –125 + (–30)
b. +105 – (–55)
c. +105 + (+55)
d. +80 – (–150)
e. +80 + (+150)
f. –99 – (–200)
g. –99 + (+200)
h. +1500 – (–1500)
Answer:
a. –125 + (–30) = (–155)
b. +105 – (–55) = (+160)
c. +105 + (+55) = (+160)
d. +80 – (–150) = (+230)
e. +80 + (+150) = (+230)
f. –99 – (–200) = (+101)
g. –99 + (+200) = (+101)
h. +1500 – (–1500) = (+3000)
|
The Other Side of Zero Class 6 Question answers Page number: 253 |
Figure it Out
Question 1: Mark 3 positive numbers and 3 negative numbers on the number line above.
Answer:
Question 2: Write down the above 3 marked negative numbers in the following boxes:
Answer:
Question 3: Is 2 > – 3? Why? Is –2 < 3? Why?
Answer:
2 > –3 as to go from 2 to –3, you have to move backwards, and –2 < 3 as to go from –2 to 3, you have to move forward. If a number is on the right-hand side of another number in the number line, then the former number is greater than the latter number and vice versa.
Question 4: What are:
a. –5+0
b. 7+(–7)
c. –10+20
d. 10 –20
e. 7–(–7)
f. –8–(–10)?
Answer:
a. –5 + 0 = –5,
b. 7 + (–7) = 0,
c. –10 + 20 = +10,
d. 10 – 20 = –10,
e. 7 – (–7) = +14,
f. –8 – (–10) = +2
|
The Other Side of Zero Class 6 Question answers Page number: 255 |
Question 1:
Use unmarked number lines to evaluate these expressions:
-
–125 + (–30) = _______
-
+105 – (–55) = _______
-
+80 – (–150) = _______
-
–99 – (–200) = _______
Answer:
a.) –125 + (–30) = ( –155)
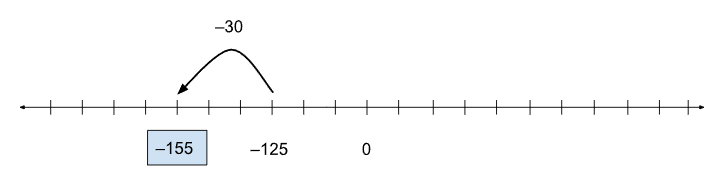
b.) +105 – (–55) = ?, or (–55) + ? = +105, or (–55) + (+160) = +105
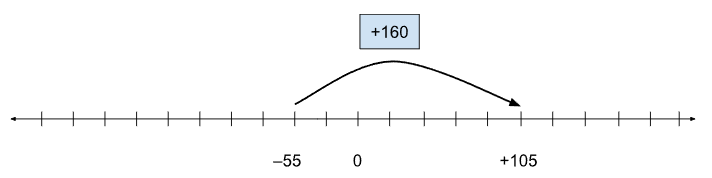
c.) +80 – (–150) = ?, or (–150) + ? = +80, or (–150) + (+230) = +80
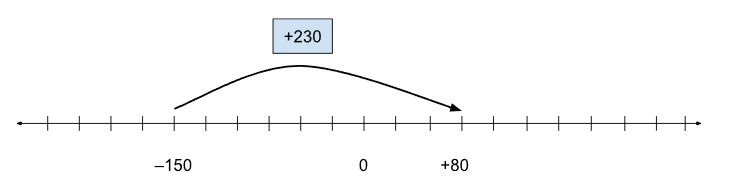
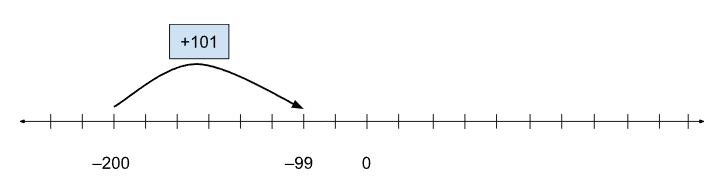
d.) –99 – (–200) = ?, or (–200) + ? = (–99), or (–200) + (+101) = (–99)
|
The Other Side of Zero Class 6 Question answers Page number: 257 |
Figure it Out
Question 1: Complete the additions using tokens.
a. (+6) + (+4)
b. (–3) + (–2)
c. (+5) + (–7)
d. (–2) + (+6)
Answer:
a.) (+6) + (+4)
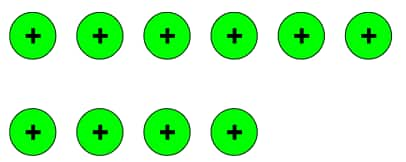
Combining 6 positive tokens and 4 positive tokens, we get a total of 10 positive tokens.
So, (+6) + (+4) = (+10)
b.) (–3) + (–2)
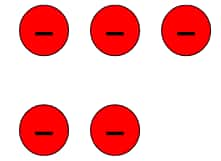
Adding 3 negative tokens to 2 negative tokens, we get a total of 5 negative tokens.
So, (–3) + (–2) = (–5)
c.) (+5) + (–7)
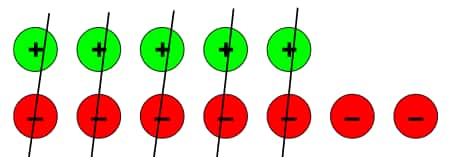
After removing five zero pairs, we are left with 2 negative tokens.
So, (+5) + (–7) = (–2)
d.) (–2) + (+6)
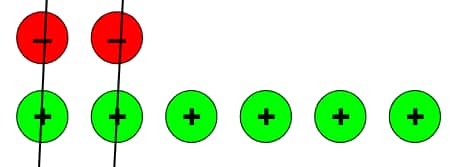
After removing two zero pairs, we are left with 4 positive tokens.
So, (–2) + (+6) = (+4).
Question 2: Cancel the zero pairs in the following two sets of tokens. On what floor is the lift attendant in each case? What is the corresponding addition statement in each case?
a.)
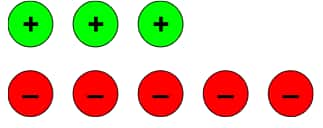
b.)
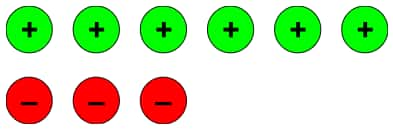
Answer:
a.)
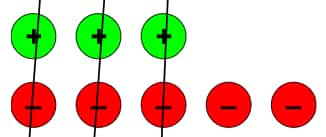
After removing the three zero pairs, we are left with 2 negative tokens.
So, the lift attendant is on the floor (–2).
The corresponding addition statement is (+3) + (–5) = (–2).
b.)
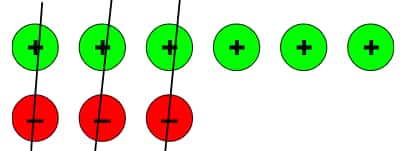
After removing the three zero pairs, we are left with 3 positive tokens.
So, the lift attendant is on the floor (+3).
The corresponding addition statement is (+6) + (–3) = (+3).
|
The Other Side of Zero Class 6 Question answers Page number: 258 |
Figure it Out
Question 1: Evaluate the following differences using tokens. Check that you get the same result as with other methods you now know:
-
(+10) – (+7)
-
(–8) – (–4)
-
(–9) – (–4)
-
(+9) – (+12)
-
(–5) – (–7)
-
(–2) – (–6)
Answer:
a.) (+10) – (+7)
From 10 positive tokens, we take away 7 positive ones, and are left with 3 positive tokens.
Also, from imagining the lift we can get (+10) – (+7) = (+3)
b.) (–8) – (–4)
From 8 negative tokens, we take away 4 negative ones, and are left with 4 negative tokens.
Also, from imagining the lift we can get (–8) – (–4) = (–4)
c.) (–9) – (–4)
From 9 negative tokens, we take away 4 negative ones, and are left with 5 negative tokens.
Also, from imagining the lift we can get (–9) – (–4) = (–5)
d.) (+9) – (+12)
To solve this, we have to put 3 extra zero pairs,
After taking out 12 positives, we are left with 3 negative tokens.
Also, from imagining the lift we can get (+9) – (+12) = (–3)
e.) (–5) – (–7)
To solve this, we have to put 2 extra zero pairs.
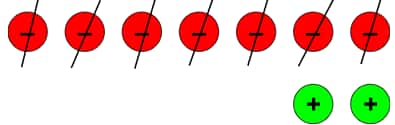
After taking out 7 negatives, we are left with 2 positive tokens.
Also, from imagining the lift we can get (–5) – (–7) = (+2).
f.) (–2) – (–6)
To solve this, we have to put 4 extra zero pairs.
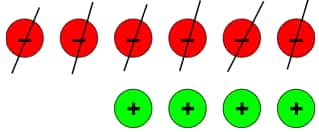
After taking out 6 negatives, we are left with 4 positive tokens.
Also, from imagining the lift we can get (–2) – (–6) = (+4).
Question 2: Complete the subtractions:
-
(–5) – (–7)
-
(+10) – (+13)
-
(–7) – (–9)
-
(+3) – (+8)
-
(–2) – (–7)
-
(+3) – (+15)
Answer:
a.) (–5) – (–7)
To solve this, we have to put 2 extra zero pairs.
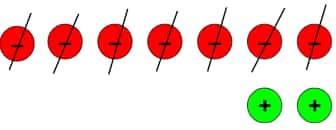
After taking out 7 negatives, we are left with 2 positive tokens.
So, (–5) – (–7) = (+2).
b.) (+10) – (+13)
To solve this, we have to put 3 extra zero pairs.
After taking out 13 positives, we are left with 3 negative tokens.
So, (+10) – (+13) = (–3)
c.) (–7) – (–9)
To solve this, we have to put 2 extra zero pairs.
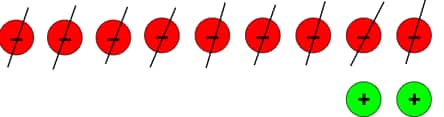
After taking out 9 negatives, we are left with 2 positive tokens.
So, (–7) – (–9) = (+2).
d.) (+3) – (+8)
To solve this, we have to put 5 extra zero pairs.
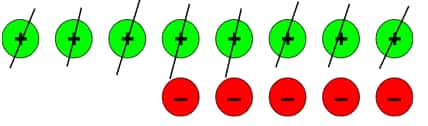
After taking out 8 positives, we are left with 5 negative tokens.
So, (+3) – (+8) = (–5).
e.) (–2) – (–7)
To solve this, we have to put 5 extra zero pairs.
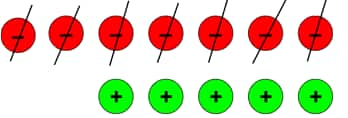
After taking out 7 negatives, we are left with 5 positive tokens.
So, (–2) – (–7) = (+5).
f.) (+3) – (+15)
After taking out 15 positives, we are left with 12 negative tokens.
So, (+3) – (+15) = (–12).
|
The Other Side of Zero Class 6 Question answers Page number: 259 |
Figure it Out
Question 1: Try to subtract: (–3) – (+5). How many zero pairs will you have to put in? What is the result?
Answer:
(–3) – (+5)
Since we have to take out 5 positive tokens, we must put down 5 zero pairs.
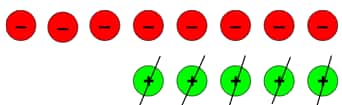
Therefore, (–3) – (+5) = (–8)
Question 2: Evaluate the following using tokens.
-
(–3) – (+10)
-
(+8) – (–7)
-
(–5) – (+9)
-
(–9) – (+10)
-
(+6) – (–4)
-
(–2) – (+7)
Answer:
a.) (–3) – (+10)
Therefore, (–3) – (+10) = (–13)
b.) (+8) – (–7)
Therefore, (+8) – (–7) = (+15)
c.) (–5) – (+9)
Therefore, (–5) – (+9) = (–14)
d.) (–9) – (+10)
Therefore, (–9) – (+10) = (–19)
e.) (+6) – (–4)
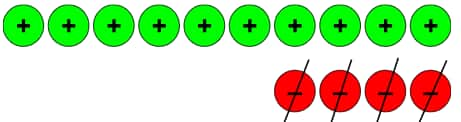
Therefore, (+6) – (–4) = (+10)
f.) (–2) – (+7)
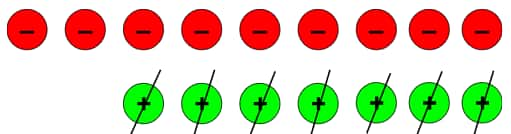
Therefore, (–2) – (+7) = (–9)
|
The Other Side of Zero Class 6 Question answers Page number: 260 |
Figure it Out
Question 1: Suppose you start with ₹0 in your bank account, and then you have credits of ₹30, ₹40, and ₹50, and debits of ₹40, ₹50, and ₹60. What is your bank account balance now?
Answer:
Starting balance = ₹0
Total credit = (+30) + (+40) + (+50) = ₹(+120)
Total debit = (+40) + (+50) + (+60) = ₹(+150)
So, the account balance = (+120) – (+150) = ₹(–30)
Question 2: Suppose you start with ₹0 in your bank account, and then you have debits of ₹1, 2, 4, 8, 16, 32, 64, and 128, and then a single credit of ₹256. What is your bank account balance now?
Answer:
Starting balance = ₹0
Total credit = ₹(+256)
Total debit = (+1) + (+2) + (+4) + (+8) + (+16) + (+32) + (+64) + (+128) = ₹(+255)
So, the account balance = (+256) – (+255) = ₹(+1)
Question 3: Why is it generally better to try to maintain a positive balance in your bank account? What are the circumstances under which it may be worthwhile to temporarily have a negative balance?
Answer:
It is generally better to try to maintain a positive balance in your bank account because:
-
i.) Banks charge a fine if the balance becomes negative.
-
ii.) A positive balance in your bank account helps in maintaining your credit score, which helps in getting loans or credit cards easily.
There are some circumstances in which it may be worthwhile to temporarily have a negative balance:
-
i.) You need money for something emergency, like hospital bills, and will soon repay the overdraft amount.
-
ii.) You are expecting huge profit margins and need some necessary money for that.
|
The Other Side of Zero Class 6 Question answers Page number: 261 |
Figure it Out
Question 1: Looking at the geographical cross-section, fill in the respective heights:
A. ____________ B. ___________ C. ___________ D. _________
E. ____________ F. ____________ G. ____________
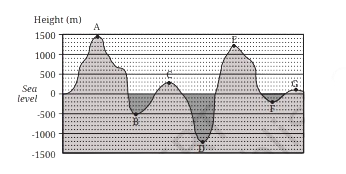
Answer:
a.) +1500 m
b.) –500 m
c.) +300 m
d.) –1200 m
e.) +1200 m
f.) –200 m
g.) +100 m
Question 2: Which is the highest point in this geographical cross-section? Which is the lowest point?
Answer:
In this geographical cross-section, the highest point is A with a height of (+1500) m.
Also, the lowest point is D with a height of (–1200) m.
Question 3: Can you write the points A, B, …, G in a sequence of decreasing order of heights? Can you write the points in a sequence of increasing order of heights?
Answer:
Points in the sequence of decreasing order of heights are A, E, C, G, F, B, D.
Also, the points in the sequence of increasing order of heights are D, B, F, G, C, E, A.
Question 4: What is the highest point above sea level on Earth? What is its height?
Answer:
The highest point above sea level on Earth is Mt. Everest, with a height of 8848 m.
Question 5: What is the lowest point with respect to sea level on land or on the ocean floor? What is its height? (This height should be negative.)
Answer:
The lowest point with respect to sea level is the Mariana Trench, in the Pacific Ocean, with a depth of 10,984 m, i.e. a height of –10,984 m.
|
The Other Side of Zero Class 6 Question answers Page number: 262 |
Figure it Out
Question 1: Do you know that there are some places in India where temperatures can go below 0°C? Find out the places in India where temperatures sometimes go below 0°C. What is common among these places? Why does it become colder there and not in other places?
Answer:
Yes, there are some places in India where temperatures can go below 0°C.
-
These places are Sikkim, Ladakh, Jammu & Kashmir, etc.
-
The common factor among these places is that they are all located near the Himalayan range.
-
It becomes colder there because they are at very high altitudes above sea level.
Question 2: Leh in Ladakh gets very cold during the winter. The following is a table of temperature readings taken during different times of the day and night in Leh on a day in November. Match the temperature with the appropriate time of the day and night.
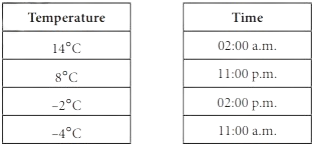
Answer:
The correct table is:
|
The Other Side of Zero Class 6 Question answers Page number: 263-264 |
Figure it Out
|
5 |
– 3 |
– 5 |
|
0 |
– 5 | |
|
– 8 |
– 2 |
7 |
Question 1: Do the calculations for the second grid above and find the border sum.
Answer:
The calculations are:
Top Row: 5 + (–3) + (–5) = –3
Bottom Row: (–8) + (–2) + 7 = –3
Left Column: 5 + 0 + (–8) = –3
Right Column: (–5) + (–5) + 7 = –3
So, the border sum of the grid is –3.
Question 2: Complete the grids to make the required border sum:
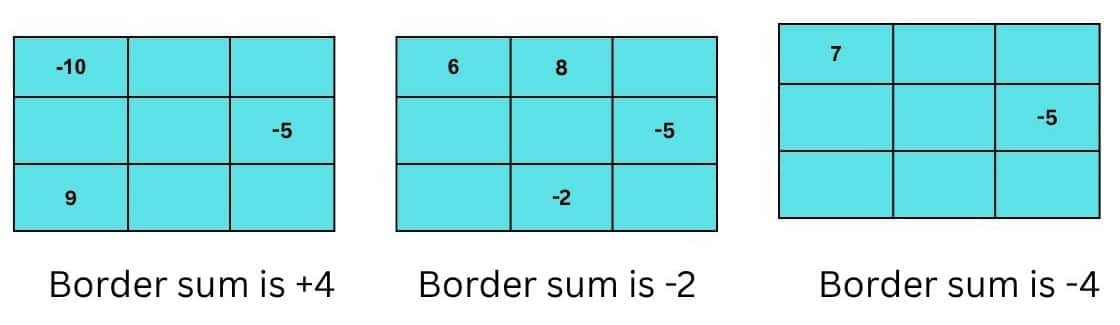
Answer:
In the first grid, we can complete it with the border sum given as +4.
|
-10 |
7 |
7 |
|
5 |
-5 | |
|
9 |
-7 |
2 |
In the second grid, we can complete it with the border sum given as –2.
|
6 |
8 |
-16 |
|
11 |
-5 | |
|
-19 |
-2 |
19 |
In the third grid, we can complete it with the border sum given as –4.
|
7 |
3 |
-14 |
|
2 |
-5 | |
|
-13 |
-6 |
15 |
Question 3: For the last grid above, find more than one way of filling the numbers to get the border sum –4.
Answer:
Another way to complete the last grid with a border sum of –4 is:
|
7 |
5 |
-16 |
|
-4 |
-5 | |
|
-7 |
-14 |
17 |
Question 4: Which other grids can be filled in multiple ways? What could be the reason?
Answer:
Many other grids with more rows and columns are likely to have multiple solutions.
This occurs because there are more options for putting the numbers while getting the required border sum.
|
2 |
? |
? |
|
? |
5 | |
|
? |
-1 |
? |
For example, this grid (Border sum = 3) can have multiple solutions.
Question 5: Make a border integer square puzzle and challenge your classmates.
Answer:
Here is a border integer puzzle to challenge your classmates:
|
8 |
-6 |
? |
|
? |
? | |
|
7 |
? |
2 |
Border Sum = 5
|
The Other Side of Zero Class 6 Question answers Page number: 265 |
Figure it Out
Question 1: Try afresh, choose different numbers this time. What sum did you get? Was it different from the first time? Try a few more times!
Answer:
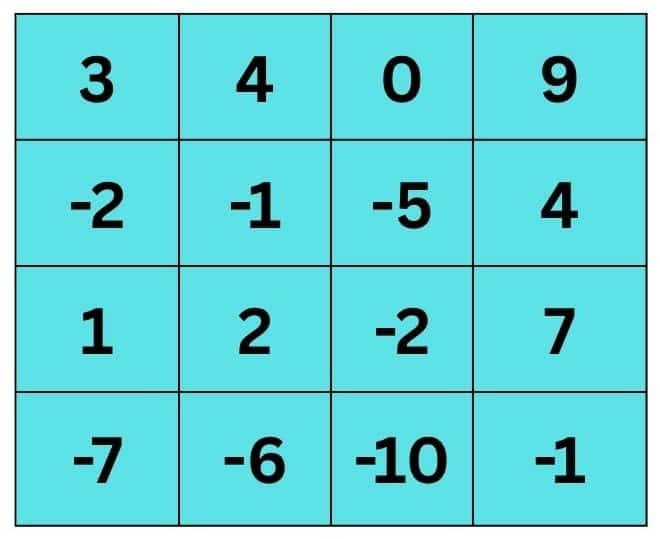
At first, circle the number (-5) and cross out the row and column that contain the number -5.
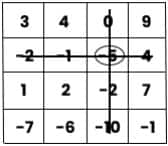
Then, circle the number (3) and cross out the row and column that contain the number 3.
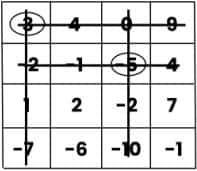
Then, circle the number (-1) and cross out the row and column that contain the number (-1).
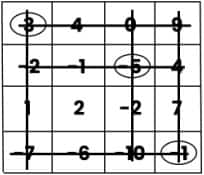
At last, circle the number (2) and cross out the row and column that contain the number 2.
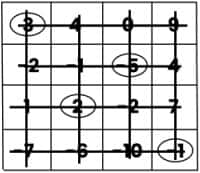
Now, let’s add the circled numbers: (-5) + 3 + (-1) + 2 = -6 + 5 = -1.
So, we are getting at the same value as -1.
Question 2: Play the same game with the grids below. What answer did you get?
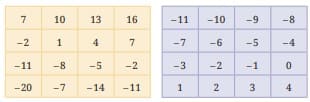
Answer:
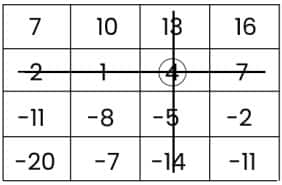
For the first grid:
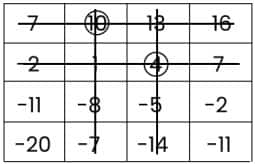
At first, circle the number (4) and cross out the row and column that contain the number 4.
Then, circle the number (10) and cross out the row and column that contain the number (10).
Then, circle the number (-20) and cross out the row and column that contain the number (-20).
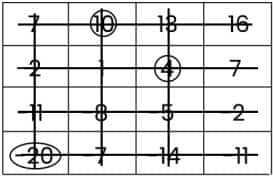
At last, circle the number (-2) and cross out the row and column that contain the number (-2).
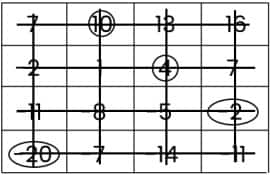
The sum all the circled numbers = 4 + (10) + (-20) + (-2) = -8
For the second grid:
At first, circle the number (-6) and cross out the row and column that contain the number (-6).
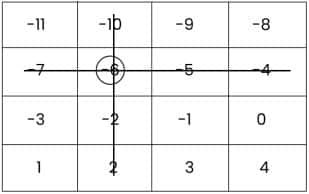
Then, circle the number (4) and cross out the row and column that contain the number (4).
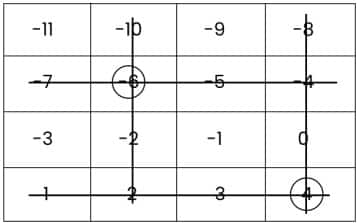
Then, circle the number (9) and cross out the row and column that contain the number (9).
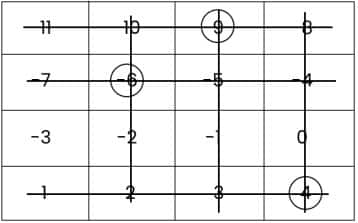
At last, circle the number (-3) and cross out the row and column that contain the number (-3).
The sum all the circled numbers = -6 + 4 + (-9) + (-3) = -2 -12 = -14.
Question 3: What could be so special about these grids? Is there magic in the numbers or the way they are arranged, or both? Can you make more such grids?
Answer:
Grids can be interesting due to both the numbers involved and their arrangement.
The numbers in a grid can give us specific patterns or sequences.
Yes, we can easily make multiple such grids.
|
The Other Side of Zero Class 6 Question answers Page number: 265-266 |
Figure it Out
Question 1: Write all the integers between the given pairs in increasing order.
a. 0 and –7
b. –4 and 4
c. –8 and –15
d. –30 and –23
Answer:
a.) The integers between 0 and –7, in increasing order, are: –6, –5, –4, –3, –2, –1.
b.) The integers between –4 and 4, in increasing order, are: –3, –2, -1, 0, 1, 2, 3.
c.) The integers between –8 and –15, in increasing order, are: –14, –13, –12, –11, –10, –9.
d.) The integers between –30 and –23, in increasing order, are: –29, –28, –27, –26, –25, –24.
Question 2: Give three numbers such that their sum is –8.
Answer:
3 numbers that add up to –8 are –5, 3, and –6.
Calculation: –5 + 3 + (–6) = –8
There can be other such pairs.
Question 3: There are two dice whose faces have these numbers: –1, 2, –3, 4, –5, 6. The smallest possible sum upon rolling these dice is –10 = (–5) + (–5) and the largest possible sum is 12 = (6)+(6). Some numbers between (–10) and (+12) are not possible to get by adding numbers on these two dice. Find those numbers.
Answer:
Let’s identify the sums that cannot be achieved when rolling these two dice. The faces of the dice show: -1, 2, -3, 4, -5, and 6.
First, let’s outline all possible sums:
The sum of two negative numbers:
(-1) + (-1) = -2
(-1) + (-3) = -4
(-1) + (-5) = -6
(-3) + (-3) = -6
(-3) + (-5) = -8
(-5) + (-5) = -10
The sum of one negative and one positive number:
(-1) + 2 = 1
(-1) + 4 = 3
(-1) + 6 = 5
(-3) + 2 = -1
(-3) + 4 = 1
(-3) + 6 = 3
(-5) + 2 = -3
(-5) + 4 = -1
(-5) + 6 =1
The sum of two positive numbers:
2 + 2 = 4
2 + 4 = 6
2 + 6 = 8
4 + 4 = 8
4 + 6 = 10
6 + 6 = 12
First of all, let’s list all the possible sums in ascending order:
–10, –8, –6, –4, –3, –2, –1, 1, 3, 4, 5, 6, 8, 10, 12.
The sum of numbers between –10 and 12 that are not possible to get by adding numbers on these two dice are:
–9, –7, –5, 0, 2, 7, 9, 11.
Question 4: Solve these:
|
8 – 13 |
(– 8) – (13) |
(– 13) – (– 8) |
(– 13) + (– 8) |
|
8 + (– 13) |
(– 8) – (– 13) |
(13) – 8 |
13 – (– 8) |
Answer:
(a) 8 – 13 = –5
(b) –8 – (13) = –8 –13 = -21
(c) (–13) – (–8) = –13 + 8 = –5
(d) (–13) + (–8) = –13 – 8 = –21
(e) 8 + (–13) = 8 – 13 = –5
(f) (–8) – (–13) = –8 + 13 = 5
(g) (13) – 8 = 13 – 8 = 5
(h) 13 – (–8) = 13 + 8 = 21
Question 5: Find the years below.
-
From the present year, which year was it 150 years ago? ________
-
From the present year, which year was it 2200 years ago? _______
Hint: Recall that there was no year 0.
-
What will be the year 320 years after 680 BCE? ________
Answer:
a.) 150 years ago from the current year (2025) is calculated as follows: 2025 – 150 = 1875. Therefore, 150 years ago, it was the year 1875.
b.) 2200 years ago from the present year (2025): 2025 – 2200 = –175.
Since there is no year 0, the year –175 corresponds to 176 BCE.
Therefore, 2200 years ago, it was the year 176 BCE.
c.) We can express 680 BCE as –680.
Therefore, 320 years after 680 BCE is calculated as: –680 + 320 = –360, which corresponds to 360 BCE.
Question 6: Complete the following sequences:
-
(–40), (–34), (–28), (–22), _____, ______, ______
-
3, 4, 2, 5, 1, 6, 0, 7, _____, _____, _____
-
_____, ______, 12, 6, 1, (–3), (–6), _____, ______, ______
Answer:
a.) (–40), (–34), (–28), (–22), _____, ______, ______.
Since –22 – (–28) = –22 + 28 = 6
–28 – (–34) = –28 + 34 = 6
–34 – (–40) = –34 + 40 = 6
This indicates that each term in the sequence increases by 6.
Therefore, the next term is: –22 + 6 = –16
The following term is: –16 + 6 = –10
The final term is: –10 + 6 = –4
Thus, the complete sequence is (–40), (–34), (–28), (–22), (–16), (–10), (–4).
b.) 3, 4, 2, 5, 1, 6, 0, 7, _____, _____, _____
Since 7 – 0 = 7
0 – 6 = –6
6 – 1 = 5
1 – 5 = –4
5 – 2 = 3
2 – 4 = –2
4 – 3 = 1
In this sequence, the numbers decrease by 1, alternating between positive and negative integers.
Thus, the next numbers are:
7 + (–8) = –1
–1 + 9 = 8
8 – 10 = –2
The complete sequence is 3, 4, 2, 5, 1, 6, 0, 7, –1, 8, –2.
c.) _____, ______, 12, 6, 1, (–3), (–6), _____, ______, ______
(–6) – (–3) = –6 + 3 = –3
(–3) – 1 = –4
1 – 6 = –5
6 – 12 = –6
This shows that in this sequence, a negative integer is added to each number.
Let’s denote the first number as x and the second number as y.
For the second number: 12 – y = –7
Thus, y = 12 + 7 = 19.
Now, for the first number, let it be x:
From 19 – x = –8, we get x = 19 + 8 = 27.
Next, let’s find the 8th number, which we’ll call a.
From a – (–6) = –2, we get a = –2 – 6 = –8.
Now, let’s determine the 9th number, referred to as b:
From b – (–8) = –1 So, b = –1 – 8 = –9.
And the last term will also be –9.
Therefore, the complete sequence is: 27, 19, 12, 6, 1, (–3), (–6), (–8), (–9), (–9).
Question 7: Here are six integer cards: (+1), (+7), (+18), (–5), (–2), (–9). You can pick any of these and make an expression using addition(s) and subtraction(s). Here is an expression: (+18)+(+1)–(+7) – (–2), which gives a value (+14). Now, pick cards and make an expression such that its value is closer to (– 30).
Answer:
(+1), (+7), (+18), (–5), (–2), (–9).
Let’s try to make an expression using addition(s) and subtraction(s), such that its value is closer to (– 30).
The possible expression is: (–9) + (–2) – (–5) – (+18) – (+7) + (+1)
The value of this expression is calculated as:
(+1) – (+7) – (+18) – (–5) + (–2) + (–9)
= 1 – 7 – 18 + 5 – 2 – 9
= (– 7 – 18 – 2 – 9) + (1 + 5)
= (–36) + 6
= –30, it is exactly (– 30).
Question 8: The sum of two positive integers is always positive, but a (positive integer) – (positive integer) can be positive or negative. What about
a. (positive) – (negative) b. (positive) + (negative)
c. (negative) + (negative) d. (negative) – (negative)
e. (negative) – (positive) f. (negative) + (positive)
Answer:
a.) (Positive) – (Negative):
Subtracting a negative number is equivalent to adding its positive counterpart, which will always yield a positive result. For example, 7 – (–2) = 7 + 2 = 9.
b.) (Positive) + (Negative):
The outcome depends on the value of the numbers involved.
If the positive number is greater, the result will be positive; if the negative number is greater, the result will be negative. For example: 9 + (–4) = 5 (positive) and 5 + (–7) = –2 (negative)
c.) (Negative) + (Negative):
Adding two negative numbers always produces a negative result.
For example, –3 + (–5) = –8.
d.) (Negative) – (Negative):
If the first negative number has a greater value, the result will be negative. In other words, if the first negative number has a smaller value than the second, the result will be positive.
For example: 5 + (–4) = 1 (positive) and –3 + (–5) = –8 (negative).
e.) (Negative) – (Positive):
This will always result in a negative value because you are subtracting a positive number from a negative one.
For instance, –4 – 2 = –6.
f.) (Negative) + (Positive):
The result depends on the values of the numbers. If the positive number is greater, the outcome will be positive; if the negative number is greater in value, the result will be negative.
For example: –2 + 5 = 3 (positive) –6 + 3 = –3 (negative)
Question 9: This string has a total of 100 tokens arranged in a particular pattern. What is the value of the string?
Answer:
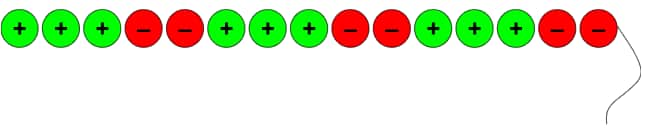
The pattern of the sequence of the string: 3, –2, 3, –2, 3, –2.
Since the pattern repeats, we can group the tokens into sets of 5,
where the total for each set is 3 – 2 = 1.
With 100 tokens in the string, we have: Total sets = $\frac{100}5=20$ sets.
Therefore, the overall value of the string is 1 × 20 = 20
|
The Other Side of Zero Class 6 Question answers Page number: 268 |
Figure it Out
Question 1: Can you explain each of Brahmagupta’s rules in terms of Bela’s Building of Fun, or in terms of a number line?
Answer:
Brahmagupta’s Rules
a.) Addition of Positive Numbers:
When adding two positive numbers, the result is positive.
Bela’s Building: Imagine Bela starts on the 3rd floor. If she moves up 2 floors, she reaches the 5th floor.
Number Line: This is like moving from 3 to 5 by adding 2.
b.) Addition of Negative Numbers:
Adding two negative numbers results in a negative number.
Bela’s Building: If Bela begins 3 floors below ground level (-3) and goes down another 2 floors, she ends up 5 floors below ground (-5).
Number Line: This is represented by moving from -3 to -5 by adding -2.
c.) Addition of a Positive and a Negative Number:
Subtract the smaller absolute value from the larger absolute value and keep the sign of the larger one.
Bela’s Building: If Bela starts on the 3rd floor and moves down 5 floors, she ends up 2 floors below ground (-2).
Number Line: This is like moving from 3 to -2 by adding -5.
d.) Subtraction of a Positive Number from a Negative Number:
Subtracting a positive number from a negative one is the same as adding both numbers and keeping the negative sign.
Bela’s Building: If Bela is 3 floors below ground (-3) and goes down 2 more floors, she ends up 5 floors below ground (-5).
Number Line: This is shown as moving from -3 to -5 by subtracting 2.
e.) Subtraction of a Negative Number from a Positive Number:
Subtracting a negative number from a positive number is equivalent to adding the two numbers.
Bela’s Building: If Bela starts on the 3rd floor and goes up 2 floors, she reaches the 5th floor.
Number Line: This is like moving from 3 to 5 by subtracting -2.
f.) Subtraction of a Negative Number from a Negative Number:
Subtracting a negative number from another negative number is the same as adding their absolute values while keeping the negative sign.
Bela’s Building: If Bela is 3 floors below ground (-3) and moves up 2 floors, she ends up 1 floor below ground (-1).
Number Line: This is like moving from -3 to -1 by subtracting -2.
Question 2: Give your own examples of each rule.
Answer:
Examples of each rule:
a.) Addition of Positive Numbers:
Example: 6 + 3 = 9
Bela’s Building: Starting on the 6th floor and moving up 3 floors to reach the 9th floor.
b.) Addition of Negative Numbers:
Example: −7 + (−4) = −11
Bela’s Building: Starting 7 floors below ground and moving down 4 more floors, reaching 11 floors below ground.
c.) Addition of a Positive and a Negative Number:
Example: 9 + (−6) = 3
Bela’s Building: Starting on the 9th floor and moving down 6 floors, arriving at the 3rd floor.
d.) Subtraction of a Positive Number from a Negative Number:
Example: −5 − 4 = −9
Bela’s Building: Starting 5 floors below ground and moving down 4 more floors to 9 floors below ground.
e.) Subtraction of a Negative Number from a Positive Number:
Example: 4 − (−3) = 7
Bela’s Building: Starting on the 4th floor and moving up 3 floors to reach the 7th floor.
f.) Subtraction of a Negative Number from a Negative Number:
Example: −6 − (−2) = −4
Bela’s Building: Starting 6 floors below ground and moving up 2 floors to end up 4 floors below ground.
NCERT The Other Side of Zero Class 6 Maths Chapter 10: Topics
Students will explore the following topics in NCERT Class 6 Maths Chapter 10 The Other Side of Zero:
- Introduction to Integers
- Number Line
- Floors in a Building (Building of Fun)
- Addition and Subtraction of Integers
- Additive Inverse
- Comparing Integers
- Real-Life Examples of Integers
- Token Model
- Brahmagupta’s Rules
Class 6 Maths Chapter 10 The Other Side of Zero solutions: Extra Questions
Question 1:
On a number line, Komal walks 7 steps to the right of zero and then 10 steps to the left.
(a) Where does she finally reach?
(b) Write this position as an integer.
(c) What does this tell us about the “other side of zero”?
Answer:
(a) First, 7 steps to the right of zero means +7.
Then, 10 steps to the left of zero means we subtract 10:
+7 – 10 = –3
So, Komal finally reaches (–3).
(b) Her position is at (–3), which is a negative integer.
(c) This shows that numbers less than zero lie on the other side of zero on the number line.
These are called negative numbers (–1, –2, –3, …). They represent values smaller than zero, such as debts, temperatures below freezing, or steps backwards.
Question 2:
In a building, the ground floor is numbered 0. Floors below it are –1, –2, –3.
Which floor is two floors below the ground floor?
Answer:
–2 floor is two floors below the ground floor.
Question 3:
What is the additive inverse of:
a) 6
b) –10
Answer:
a) Additive inverse of 6 = –6
b) Additive inverse of –10 = 10
Question 4:
Write integers to represent the following:
a) Loss of ₹50
b) Temperature 5°C above zero
Answer:
a) –50
b) +5
Question 5:
Using Brahmagupta’s rule, find: (–4) + (–6)
Answer:
–4 + (–6) = –(4 + 6) = –10
NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Notes
Careers360 has prepared these Class 6 The Other Side of Zero Notes to make your revision smoother and faster. Additionally, these notes will help students understand the The Other Side of Zero NCERT solutions and solve them independently from next time.
Positive numbers and Negative numbers
Positive numbers: It is the numbers which are greater than zero, like 1, 2, 3, …
Negative numbers: It is those numbers which are less than zero, like 1, –2, –3, …
Zero (0): It is neither a positive number nor a negative number.
Integers
It is the set of numbers which includes all positive and negative whole numbers and zero.
Example: ….. –3, –2, –1, 0, 1, 2, 3, …..
Number Line
It is a straight line where each point on the line represents a certain number. It has some properties like:
Numbers to the right of zero are positive.
Numbers to the left of zero are negative.
Examples: Building of Fun
A building has floors above and below the ground.
Ground floor = 0.
Floors above ground (like +1, +2) are positive.
Floors below ground (like –1, –2) are negative.
Example: To reach Floor +2 from 0, press the + button twice.
Addition of Integers
Rule:
Starting number + movement = target number
Examples:
(+1) + (+2) = +3 (move up 2 floors from +1 to reach +3)
(–2) + (+4) = +2 (move up 4 floors from –2 to reach +2)
Subtraction of Integers
Rule:
Target number – starting number = movement
Examples:
(+4) – (+1) = +3
(–1) – (–3) = +2
We can also convert subtraction to addition:
Subtracting a negative number is like adding a positive number.
Example: 5 – (–3) = 5 + 3 = 8.
Additive Inverse (Opposites)
Every integer has an additive inverse — a number that makes the sum zero.
Example:
Inverse of +3 is –3 (because 3 + (–3) = 0)
The inverse of –4 is +4.
Comparing Integers
Positive numbers are always greater than zero, and any negative number.
The more negative a number, the smaller it is.
Example:
–4 < –3
0 > –5
5 > –2
Real-Life Uses of Integers
Bank accounts: Debits (–) and credits (+).
Temperatures: Below zero (like –5°C in winter).
Heights: Above and below sea level.
Token Model (Visual Model)
Positive tokens = + numbers
Negative tokens = – numbers
Zero pairs: One positive and one negative cancel each other.
Example:
(+5) + (–3) = +2 (because 3 zero pairs are removed, leaving 2 positive tokens)
Brahmagupta’s Rules for Addition and Subtraction
-
Addition of Positive Numbers: When adding two positive numbers, the result is positive.
-
Addition of Negative Numbers: Adding two negative numbers results in a negative number.
-
Addition of a Positive and a Negative Number: Subtract the smaller absolute value from the larger absolute value and keep the sign of the larger one.
-
Subtraction of a Positive Number from a Negative Number: Subtracting a positive number from a negative one is the same as adding both numbers and keeping the negative sign.
NCERT Solutions for Class 6 Maths Chapter 10 The Other Side of Zero: Points to Remember
Check the following important points to understand and solve Class 6 Maths Chapter 10 The Other Side of Zero question answers effectively.
- Integers include all positive numbers, negative numbers, and zero.
- A number line has zero in the centre, with positive numbers to the right and negative numbers to the left.
- Use the number line to add or subtract integers. Adding a negative number means moving backwards, while subtracting a negative number is like adding a positive number.
- On the number line, numbers to the right are greater, and numbers to the left are smaller.
Why are Class 6 Maths Chapter 10 The Other Side of Zero question answers important?
The chapter, The Other Side of Zero, of Class 6 is an important part of number systems. This chapter mainly focuses on negative numbers and their operations. Here’s why the Class 6 Maths The Other Side of Zero question answers are important.
- Negative numbers are important in the number system, and the practice of identifying and operating on negative numbers helps students to deal with higher-level problems in later classes.
- This chapter also builds the base for algebra, coordinate geometry and many real-life problems such as temperature change, debt or loss calculation.
- Questions from this chapter often come in competitive exams such as Olympiads, NTSE and other school-level exams.
NCERT Solutions for Class 6 Mathematics Chapter Wise
We at Careers360 compiled all the NCERT Class 6 Maths Solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and NCERT Syllabus
Students can also check the NCERT Books and the NCERT Syllabus for Class 6 here:
Frequently Asked Questions (FAQs)
Q: Why is the chapter called The Other Side of Zero?
A:
This chapter explores numbers that lie to the left of zero on the number line, which are called negative numbers.
Q: Can I download the NCERT Solutions for Class 6 Maths Chapter 10 in PDF format?
A:
Yes, many educational platforms, such as Careers360, offer free downloadable PDFs of The Other Side of Zero Class 6 NCERT Solutions. Students can find the free downloadable PDF in this article itself.
Q: Why are negative numbers important in mathematics?
A:
Negative numbers are used in real-life situations such as measuring temperatures below zero, bank balances, elevations, and profits/losses.
Q: What is an additive inverse?
A:
The additive inverse of a number is the number that, when added to it, gives zero.
Example: The additive inverse of +5 is (–5).
Q: What are Brahmagupta’s rules about?
A:
Brahmagupta’s rules explain how to add, subtract, multiply, and divide positive and negative numbers.
Q: Where do we find negative numbers in real life?
A:
Negative numbers are used to show temperatures less than zero, debt, altitude below sea level, or score loss in games.
Q: How are negative numbers shown on the number line?
A:
On a number line, negative numbers are placed to the left of zero, while positive numbers are placed to the right.
Q: Can zero be considered positive or negative?
A:
No, zero is neither positive nor negative. It is a neutral number.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters