NCERT Solutions for Class 6 Maths Chapter 1 - Patterns in Mathematics
Patterns make maths fun, like solving a puzzle. If we observe closely, we will see patterns exist all around us, such as in nature, in our homes and schools, etc. We can find them almost everywhere in our lives in the form of numbers, shapes, etc. NCERT Class 6 Maths Chapter 1 Patterns in Mathematics includes the fundamental patterns in numbers. These NCERT Solutions are designed in such a manner that they help students strengthen their conceptual clarity and improve problem-solving and analytical skills. It will help make understanding simple and clear. Many teachers recommend NCERT Solutions because they closely match the exam pattern.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 1 Patterns in Mathematics: Download Free PDF
- NCERT Solutions for Class 6 Maths Chapter 1 Patterns in Mathematics
- Patterns in Mathematics Class 6 Maths Chapter 1: Topics
- NCERT Solutions for Class 6 Maths Chapter 1 Patterns in Mathematics: Notes
- NCERT Class 6 Maths Chapter 1 Patterns in Mathematics Solutions: Points to Remember
- Class 6 Maths Chapter 1 Patterns in Mathematics solutions: Extra Question
- Why are Class 6 Maths Chapter 1 Patterns in Mathematics question answers important?
- NCERT Solutions for Class 6 Maths Chapter Wise
- NCERT Books and NCERT Syllabus

The Patterns in Mathematics Class 6 NCERT Solutions provide step-by-step explanations that help students build a strong foundation in maths with proper conceptual clarity. These NCERT Solutions of Class 6 Maths are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. NCERT Solutions for class 6 are very helpful for the students during exam preparation to practice more questions and help them face the questions with confidence. For detailed solutions, complete syllabus notes, and a free PDF download, refer to this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 1 Patterns in Mathematics: Download Free PDF
Careers360 brings you NCERT Solutions for Class 6 Maths Chapter 1, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 1 Patterns in Mathematics
Given below are the detailed Class 6 Maths Chapter 1 Patterns in Mathematics question answers given in the textbook.
| Patterns in Mathematics Class 6 Question Answers Page number: 2 Question: 2 |
Question 1: Can you think of other examples where mathematics helps us in our everyday lives?
Answer:
Mathematics is very useful in our daily lives. It helps us manage different activities more easily and accurately. Some areas where mathematics is important are:
a) Shopping and Budget:
When we shop, we often calculate discounts, compare prices, and plan how much we can spend.
Example: Suppose a bag costs ₹ 1200, and there is a 25% discount.
We calculate the discount as $\frac{25}{100} \times 1200=300$.So, the final price of the bag is ₹1200 - ₹ 300 = ₹ 900.
b) Navigation and Travelling:
While travelling, we use mathematics to find distance, time, and speed.
Example: If you need to travel 100 kilometres and your car moves at a speed of 50 kilometres per hour,
the time taken $=$ Distance $\div$ Speed $=\frac{100}{50}=2$ hours.
c) Science and Technology:
Mathematics is the base of scientific experiments, computer programming, and technology development.
Example: Mobile phones use mathematics (like prime numbers and codes) to protect our information while calling or sending messages.
Question 2: How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses, or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Answer:
In addition to helping us understand the world, it is a practical use of mathematics, such as helping more powerful medical means, making it important for science and technology.
Diagnostic imaging uses mathematical algorithms and imaging techniques to reconstruct, assess, and interpret medical images obtained from X-rays, CT scans, MRI, ultrasound, and other imaging procedures. Engineers use math to design and construct buildings, bridges, and other structures to ensure they are safe and stable.
Math is crucial in creating and improving technologies like computers, mobile phones, and TVs. Mathematics helps scientists conduct experiments, analyse data, and make predictions.
Economists use math to model economic systems, forecast trends, and manage financial markets.
| Patterns in Mathematics Class 6 Question Answers Page number: 3 Question: 2 |
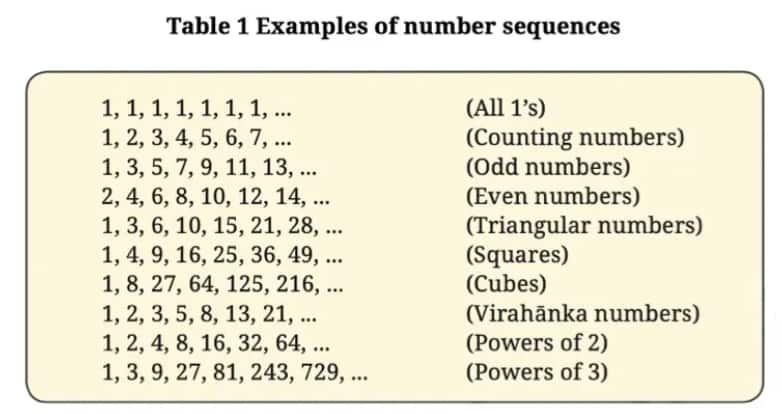
Question 1: Can you recognise the pattern in each of the sequences in Table 1?
Answer:
|
Pattern |
Recognition of a pattern |
| $1,1,1,1,1,1,1, \ldots$ (All l's) |
Sequence of all 1 's |
| $1, 2,3,4,5,6,7, \ldots$ (Counting numbers) |
A sequence of consecutive counting numbers starting from 1 |
| $1,3,5,7,9,11,13, \ldots$ (Odd numbers) |
A sequence of consecutive odd numbers starting from 1 |
|
2, 4, 6, 8, 10, 12, 14, ... (Even numbers) |
A sequence of consecutive even numbers starting from 2 |
|
1, 3, 6, 10, 15, 21, 28, ... (Triangular numbers) |
In the sequence, each term is the sum of the first n consecutive counting numbers |
|
1,4, 9, 16, 25,36, 49, ... (Squares) |
In the sequence, each term is the product of a counting number by itself, starting from 1 |
|
1, 8, 27, 64, 125, 216, ... (Cubes) |
In the sequence, each term is the product of a counting number by itself thrice, starting from 1 |
|
1, 2, 3, 5, 8, 13, 21, ... (Virahanka numbers) |
In the sequence, each term (starting from the third term) is the sum of the previous two terms. |
Question 2: Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what the rule is for forming the numbers in the sequence.
Answer:
|
Pattern |
Recognition of a pattern |
|
1,1,1,1,1,1,1, 1, 1, 1 |
Sequence of all 1 's |
|
1,2,3,4,5,6,7, 8, 9, 10 |
A sequence of consecutive counting numbers starting from 1, |
|
1,3,5,7,9,11,13, 15, 17, 19 |
A sequence of consecutive odd numbers starting from 1, adding 2 to the previous term to get the next term, |
|
2, 4, 6, 8, 10, 12, 14, 16, 18, 20 |
A sequence of consecutive even numbers starting from 2, adding 2 to the previous term to get the next term, |
|
1, 3, 6, 10, 15, 21, 28, 36, 45, 55 |
In the sequence, each term is the sum of the first n consecutive counting numbers, as |
|
1,4, 9, 16, 25,36, 49, 64, 81, 100 |
In the sequence, each term is the product of a counting number by itself, starting from 1, |
|
1, 8, 27, 64, 125, 216, 343, 512, 729 |
In the sequence, each term is the product of a counting number by itself thrice, starting from 1, as 1×1×1=1; |
|
1, 2, 3, 5, 8, 13, 21, 34, 55, 89 |
In the sequence, each term (starting from the third term) is the sum of the previous two terms, |
|
1,2,4,8,16,32,64,128,256,512 |
In the sequence, the next term is twice the previous term, as |
|
1,3,9,27,81,243,729,2187,6561,19683 |
In the sequence, the next term is three times the previous term, as |
|
Patterns in Mathematics Class 6 Question Answers |
Question 1: Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence!
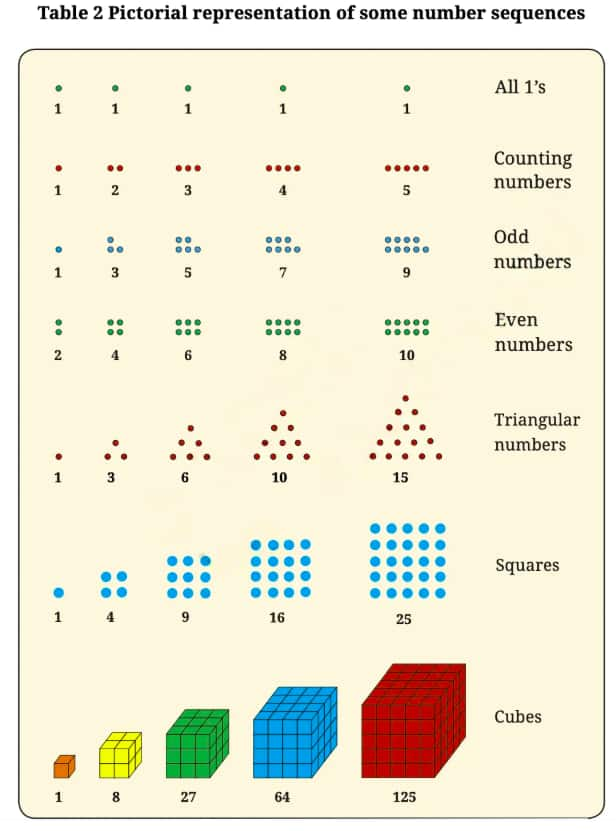
Answer:
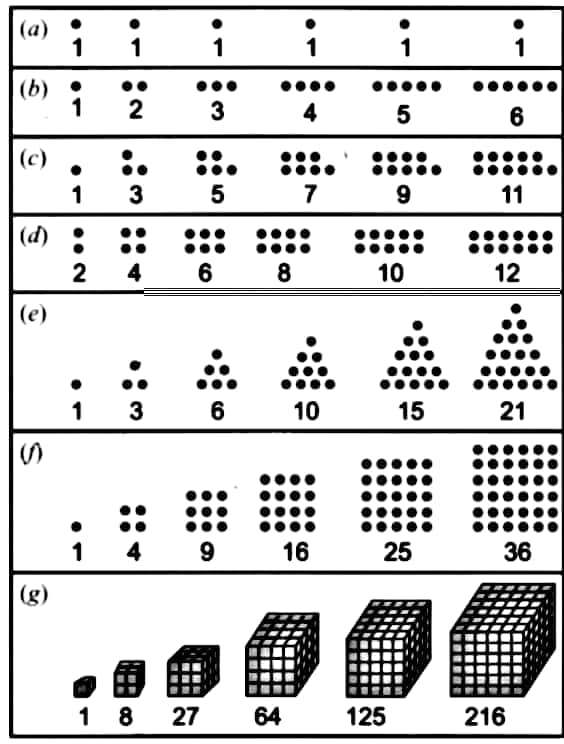
Question 2: Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers or squares? Why are 1, 8, 27, 64, 125, … called cubes?
Answer:
Triangular numbers (1,3,6,10,15,…) are called so because they can be represented by dots arranged in the shape of a triangle.
For example, 3 dots form a triangle with two at the bottom and one at the top.
Square numbers (1,4,9,16,25,…) are called squares because they can be arranged in a square grid,
like 4 dots forming a 2×2 square.
Cubes (1,8,27,64,125,…) represent the number of small cubes that fit into a larger cube, with each number being the cube of an integer.
like 3 × 3 × 3 for 27.
Question 3: You will have noticed that 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and a square. Make pictures in your notebook illustrating this! This shows that the same number can be represented differently and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Answer:
36 is a triangular number
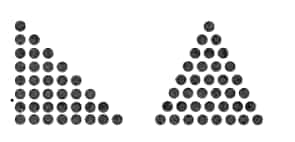
36 is a square number.

In the same way, number 9 can be represented in different ways, as,

Similarly, number 10 can be represented as a rectangle and a triangle by arranging dots, as

Question 4: What would you call the following sequence of numbers? That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
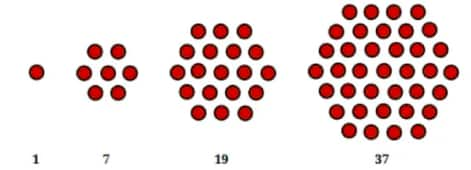
Answer:
$\begin{gathered}1 \\ 1+6=7 \\ 7+12=19 \\ 19+18=37 \\ 37+24=61\end{gathered}$
So, the next hexagonal number in the sequence is 61. It can be represented as:

Question 5: Can you think of pictorial ways to visualise the sequence of Powers of 2? Powers of 3? Here is one possible way of thinking about Powers of 2:
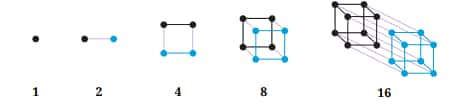
Answer:
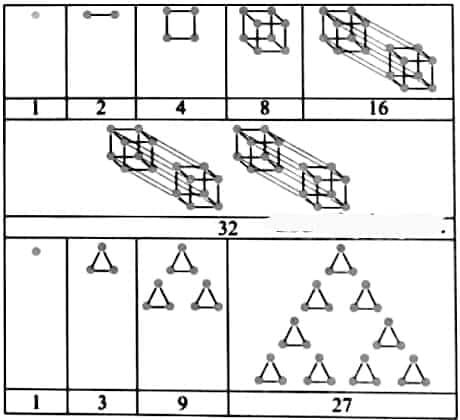
|
Patterns in Mathematics Class 6 Question Answers |
Question 1: Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, gives square numbers?
Answer:
|
|
1 |
|
|
1 + 2 + 1 = 4 |
|
|
1 + 2 + 3 + 2 + 1 = 9 |
|
|
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 |
Question 2: By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be the value of 1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1?
Answer:

$1 + 2 + 3+…+99+100+99+…+3+2+1=10000.$
Question 3: Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?
Answer:
When we add all the 1 's sequences up, we get the counting numbers, as
$\begin{gathered}1=1 \\ 1+1=2 \\ 1+1+1=3 \\ 1+1+1+1=4, \ldots\end{gathered}$
When I add all the 1's sequences up, I get a sequence of counting numbers (1,2,3,4,…).
When I add all the 1's sequences up and down, I again get a sequence of counting numbers,
but mirrored around a peak (1,2,3,2,1), forming a diamond shape.
Question 4: Which sequence do you get when you start to add the counting numbers up? Can you give a smaller pictorial explanation?
Answer:
We get the triangular numbers.
1,
1+2=3,
1+2+3=6,
1+2+3+4=10,
1+2+3+4+5=15,…
Pictorial representation:

Question 5: What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, … Which sequence do you get? Why? Can you explain it with a picture?
Answer:
When I add pairs of consecutive triangular numbers
(e.g., 1+3=4,3+6=9,6+10=16, ...), I get square numbers ( 4,9,16,… ).
This happens because each pair of triangular numbers combines to form a perfect square, and I can represent this pictorially by rearranging the dots of two triangular numbers into a square.
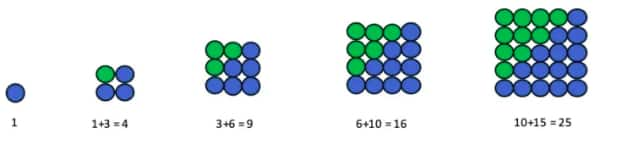
Question 6: What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 8, …? Now add 1 to each of these numbers—what numbers do you get? Why does this happen?
Answer:
When we add up powers of 2 (e.g., 1,1+2=3,1+2+4=7,1+2+4+8=15… )
And then add 1 to each sum, we get the sequence 2,4,8,16…, which are powers of 2 again.
This happens because adding the sequence of powers of 2 up to a certain point and then adding 1 results in the next power of 2.
This pattern can be visualised by pictorially doubling the size of a block of dots each time.
Question 7: What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?
Answer:
The triangular numbers are 1,3,6,10,15,21,…
After multiplying by 6 and adding 1, we get,
1×6+1=7,
3×6+1=19,
6×6+1=37,
10×6+1=61,
15×6+1=91,….
These are Hexagonal numbers.
Pictorial representation:

Question 8: What happens when you start to add up hexagonal numbers, i.e., take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, … ? Which sequence do you get? Can you explain it using a picture of a cube?
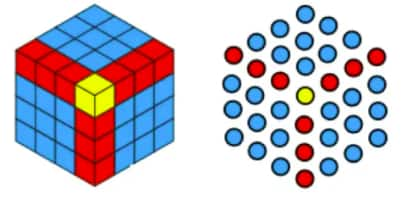
Answer:
Adding hexagonal numbers, we get
1,
1+7=8,
1+7+19=27,
1+7+19+37=64,…
Clearly, we get 1,8,27,64,125,…
It is the sequence of cubes.
Pictorial representation:
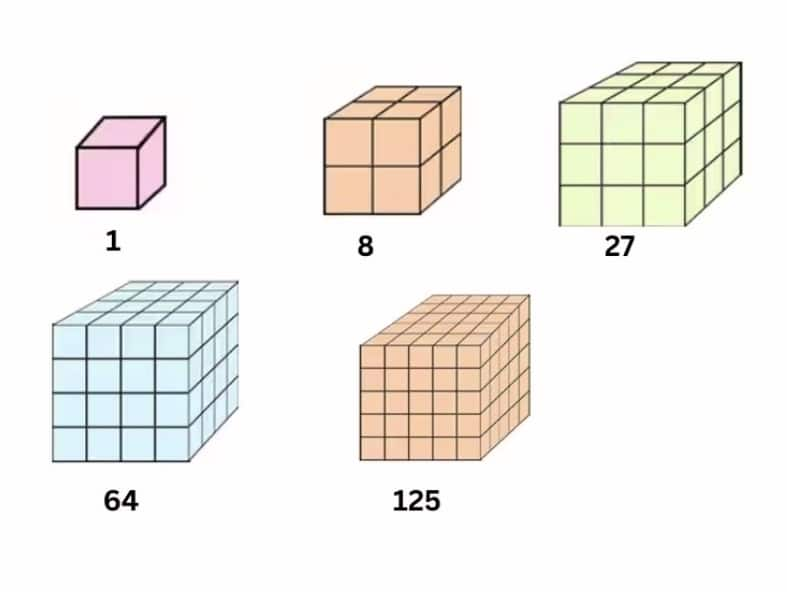
Question 9: Find your own patterns or relations in and among the sequences in Table 1. Can you explain why they happen with a picture or otherwise?
Answer:
Here are two simple patterns:
Multiples of 3:
The sequence 3,6,9,12,15,18,… includes numbers that are multiples of 3.
Each number is 3 more than the previous one.
Starting at 10 and increasing by 5:
The sequence 10,15,20,25,… starts at 10, with each number increasing by 5.
In the first sequence, each term is 3 times a whole number.
In the second sequence, each term starts at 10 and adds 5 each time.
Both sequences show how regular patterns can be created with simple rules.
Explanation with a Picture:
If we imagine forming a square by placing dots.
Start with 1 dot, then add a row of 3 dots to form a 2×2 square, then add a row of 5 dots to make a 3 × 3 square, and so on.
This shows that each square is built by adding the next odd number of dots, demonstrating why square numbers are the sum of consecutive odd numbers.
This pattern occurs because each new square is formed by extending the previous square by an L-shaped layer of dots, where the number of dots in the layer equals the next odd number.
|
Patterns in Mathematics Class 6 Question Answers |
Question 1: Can you recognise the pattern in each of the sequences in Table 3?
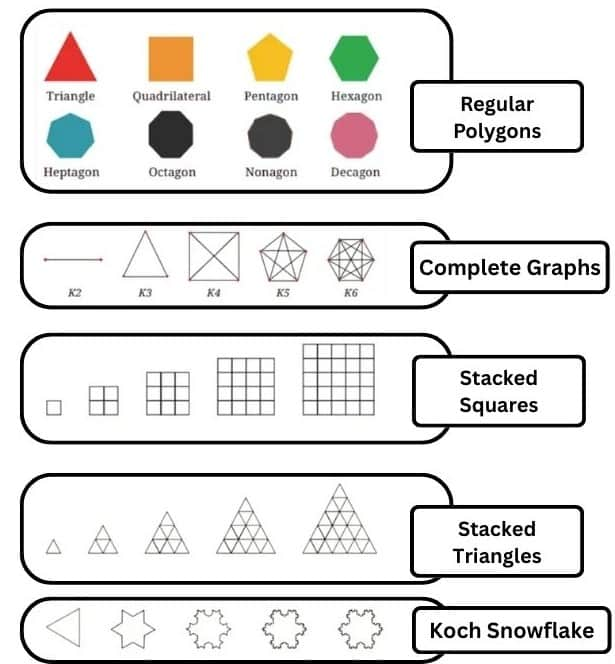
Answer:
Regular polygon:
In the sequence, the next polygon is obtained by increasing the number of sides by 1.
Examples include triangle, quadrilateral, pentagon, and hexagon.
In these shapes, the number of sides increases by 1 with each step, starting from 3. This forms a continuous number sequence where each polygon has one more side than the previous one.
Complete Graph:
In the sequence, the next shape is obtained by increasing the number of vertices by 1.
The number of lines in the sequence is as follows:
For K2=1,K3=3,K4=6,K5=10, and K6=15, The resulting series is 1,3,6,10,15,……
This forms a triangular number sequence, where each term represents the total number of lines that can form a triangle.
Triangular numbers are generated by adding consecutive natural numbers, making this sequence grow in a predictable pattern.
Stacked Squares:
In the sequence, the next bigger square represents the square numbers. The number of small squares in each layer follows the pattern: 1, 4,9,16, 25, and so on.
This sequence represents square numbers, where each term is the result of squaring a natural number $\left(1^2, 2^2, 3^2\right.$, etc.).
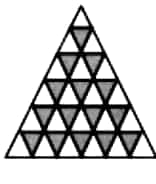
Stacked Triangles:
In the sequence, the next bigger triangle represents the sum of consecutive odd numbers starting from 1.
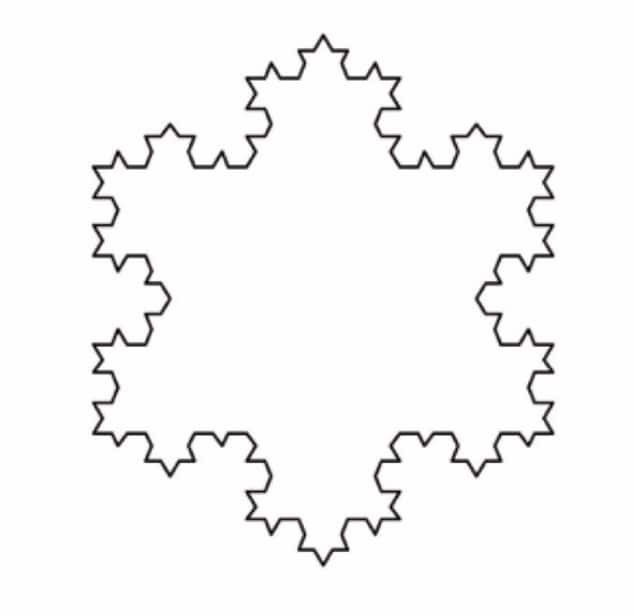
Koch Snowflake:
In the sequence, each time each line segment '-' is replaced by a speed bump 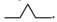 . As one does this more and more times, the changes become tinier and tinier with very, very small line segments. The number of sides in each increases by a factor of 4.
. As one does this more and more times, the changes become tinier and tinier with very, very small line segments. The number of sides in each increases by a factor of 4.
Question 2: Try to redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.
Answer:
|
Regular Polygon |
|
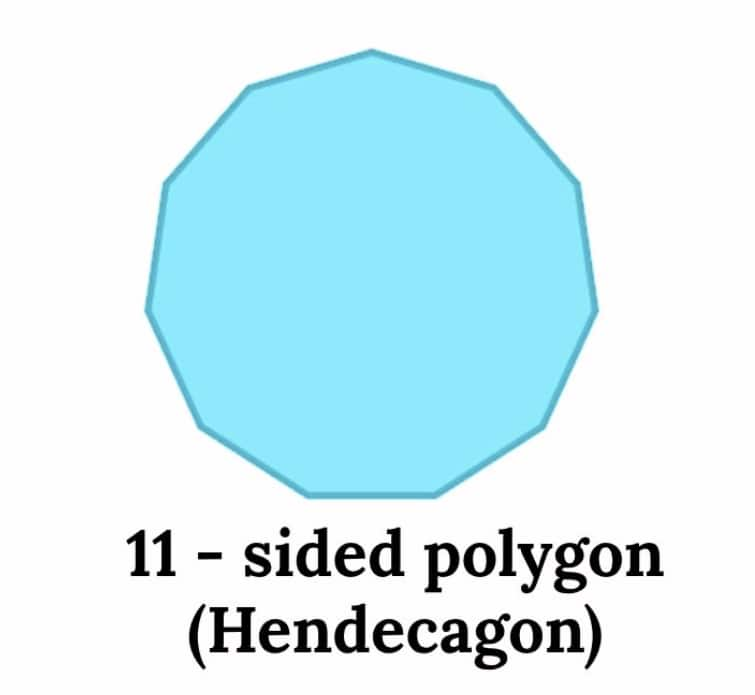
Yes, we can draw the shape. A polygon with 11 sides is known as a hendecagon. |
This is the pattern based on polygons with the number of sides increasing by 1. |
|
Complete graph |
|
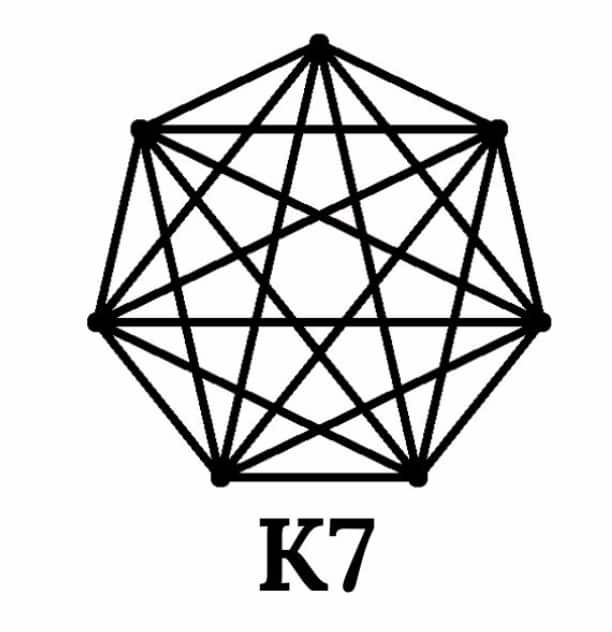
Yes, we can draw the shape. The image shows a complete graph with 7 vertices (K7), where every point is connected to every other point with straight lines. |
This is the pattern based on a complete graph; increasing the number of vertices increases by 1. |
|
Stacked Squares |
|
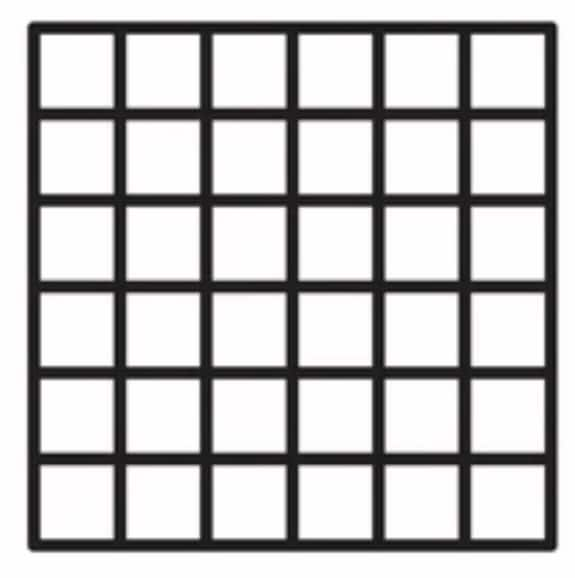
Yes, we can draw the shape. The total number of squares is 6×6=36. This calculation represents a perfect square, showing how the number of small squares forms a 6×6 grid. |
This is the pattern based on stacked squares representing the square numbers. 1,4,16,25,36,… |
|
Stacked Triangles |
|
Yes, we can draw the shape. The total number of triangles is 1+3+5+7+9+11=36. This sum represents the sequential addition of odd numbers, resulting in the total number of triangles in the arrangement. |
This is the pattern based on stacked triangles representing the sum of consecutive odd numbers starting from 1. As 1,1+3, 1+3+5, … |
|
Koch Snowflake |
|
Yes, we can draw the shape. The shape is a Koch snowflake, created by repeatedly adding triangular bumps to each side of an equilateral triangle. |
In this pattern, each time each line segment ' - ' is replaced by a speed bump. |
|
Patterns in Mathematics Class 6 Question Answers |
Question 1: Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Answer:
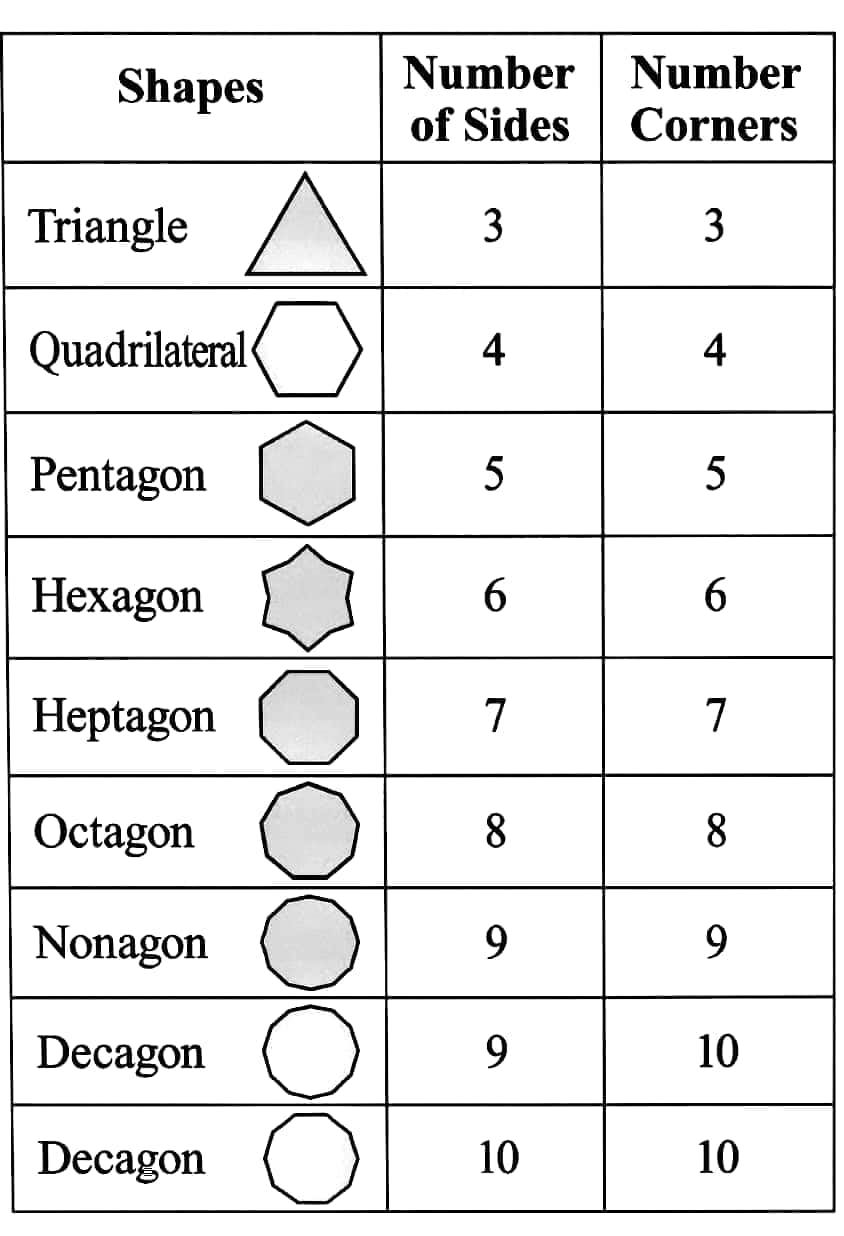
The number sequence we get is 3,4,5,6,7,8,9,10,
i.e., the counting numbers starting from 3, in both cases: number of sides and number of corners.
The sequence is the counting numbers starting from 3.
This happens because regular polygons have an equal number of sides and corners by definition, and as we move to polygons with more sides, the number of corners also increases accordingly.
This one-to-one correspondence between sides and corners results in the same sequence for both.
Question 2: Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get? Can you explain why?
Answer:
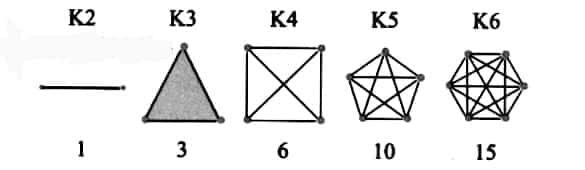
After counting the number of lines on each shape in the sequence, we get
1,3,6,10,15,21…
It is the sequence of triangular numbers because each term of the sequence obtained is the sum of n consecutive numbers.
Question 3: How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?
Answer:
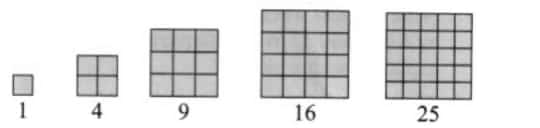
Clearly, we get a sequence of square numbers 1,4,9,16,25,… because we count the number of little squares in each shape and get each one is the product of the counting number by itself.
Question 4: How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why? (Hint: In each shape in the sequence, how many triangles are there in each row?)
Answer:
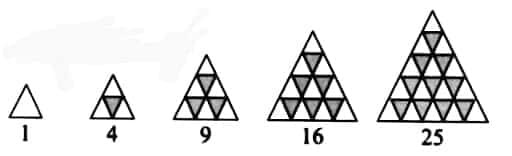
Clearly, we get a sequence of square numbers, 1,4,9,16,25,…, which are obtained by adding the number of small triangles in each row.
That is,
1,
1+3=4,
1+3+5=9,
1+3+5+7=16,…
Question 5: To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘—’ by a ‘speed bump’ . As one does this more often, the changes become tinier and tinier with very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence? (The answer is 3, 12, 48, ..., i.e., 3 times Powers of 4; this sequence is not shown in Table 1.)

Answer:
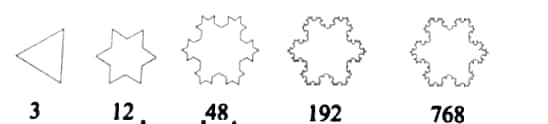
By counting line segments, we get the number sequence: 3,12,48,192,768,…
In the sequence, each term is thrice the power of 4, as
$\begin{gathered}3 \times 1=3 \\ 3 \times 4=12 \\ 3 \times(4 \times 4)=48 \\ 3 \times(4 \times 4 \times 4)=192\end{gathered}$
Patterns in Mathematics Class 6 Maths Chapter 1: Topics
Topics you will learn in NCERT Class 6 Maths Chapter 1 Patterns in Mathematics include:
- 1.1 What is Mathematics?
- 1.2 Patterns in Numbers
- 1.3 Visualising Number Sequences
- 1.4 Relations among Number Sequences
- 1.5 Patterns in Shapes
- 1.6 Relation to Number Sequences
NCERT Solutions for Class 6 Maths Chapter 1 Patterns in Mathematics: Notes
Patterns are the heartbeat of mathematics, guiding us to understand the hidden order. These notes will help you understand this chapter better and deal with the Class 6 Maths chapter 1 Patterns in Mathematics question answers with ease.
Patterns in Mathematics
Patterns are all around us. For example, the understanding of patterns in the motion of stars, planets, and their satellites helped humans to develop the theory of gravitation, and now our scientists can launch such satellites from our country, like Aditya L1, Chandrayaan, etc. Similarly, understanding patterns in biotech has helped in diagnosing and curing diseases. The list does not end here, but continues.
Patterns in Numbers
We first look at the pattern of whole numbers.
0, 1, 2, 3, 4, ...
Number theory is defined as the branch of Mathematics that studies patterns in whole numbers.
1, 1, 1, 1, 1, 1, 1,... (All 1’s)
1, 2, 3, 4, 5, 6, 7,... (Counting numbers)
1, 3, 5, 7, 9, 11, 13,... (Odd numbers)
2, 4, 6, 8, 10, 12, 14,... (Even numbers)
1, 3, 6, 10, 15, 21, 28,... (Triangular numbers)
1, 4, 9, 16, 25, 36, 49,... (Squares)
1, 8, 27, 64, 125, 216,... (Cubes)
1, 2, 3, 5, 8, 13, 21,... (Virahānka numbers)
1, 2, 4, 8, 16, 32, 64,... (Powers of 2)
1, 3, 9, 27, 81, 243, 729,... (Powers of 3)
Visualising Number Sequences
Visualising Number Sequences helps us to better understand the patterns.
Numbers such as 1, 3, 6, 10, 15,... are called triangular numbers and 1, 4, 9, 16, 25,... are called square numbers or squares
Moreover,1, 8, 27, 64, 125,... are called cubes

Relations among Number Sequences
We can establish various relations among numbers.
1 = 1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 + 5 + 7 + 9 + 11 = 36
is also a pattern in mathematics.
Another arrangement could be:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Patterns in Shapes
We can also figure out patterns in shapes. These shapes may be(1D, 2D, or 3D) or in even more dimensions. Geometry is the branch of Mathematics that studies patterns in shapes. Shape sequences are one important type of shape pattern that mathematicians study.

As an example, we also observe certain shapes in which the number of sides increases by one unit every time. Such shapes are known as regular shapes. Regular shapes can be classified as a regular triangle, a quadrilateral (i.e., square), a pentagon, a hexagon, a heptagon, etc.
NCERT Class 6 Maths Chapter 1 Patterns in Mathematics Solutions: Points to Remember
Patterns are seen everywhere around us, from nature to architecture. Mathematics can be said to be the study of various patterns and their properties. Here are some points that will help us to deal with Class 6 Maths chapter 1 Patterns in Mathematics question answers better.
Patterns in Numbers: Numbers in certain orders exhibit various patterns.
E.g., Odd numbers, even numbers, triangular numbers, squares, cubes, etc.
Patterns in Shapes: Patterns in shapes are certain arrangements of shapes like triangles, rectangles, pentagons, squares, etc.
For example, the patterns in a honeycomb are arrangements of hexagons.
Class 6 Maths Chapter 1 Patterns in Mathematics solutions: Extra Question
Question 1:
Observe the following number pattern and fill in the blanks:
2, 6, 12, 20, 30, … , … , …
Solution:
Differences between consecutive terms:
-
6 – 2 = 4
-
12 – 6 = 6
-
20 – 12 = 8
-
30 – 20 = 10
So, the differences are increasing by 2 each time.
So,
-
Next difference = 12
So, 30 + 12 = 42 -
Next difference = 14
So, 42 + 14 = 56 -
Next difference = 16
So, 56 + 16 = 72
Hence, the full pattern is 2, 6, 12, 20, 30, 42, 56, 72.
The missing numbers are 42, 56, and 72.
Question 2:
Are 1, 4, 9, 16 related? How?
Answer:
Yes. They are squares of numbers.
1², 2², 3², 4²
Question 3:
Complete the pattern:
○ △ ○ △ ___ ___
Answer: ○ △
Explanation: The pattern repeats a circle and a triangle.
Question 4:
How many matchsticks are needed to make 3 squares in a row?
Answer:
10 matchsticks
Explanation: Adjacent squares share sides, so fewer sticks are needed.
Question 5:
How many dots will be there in the 4th figure if 2 dots are added each time?
Answer:
7 dots
Explanation:
1st: 1 dot
2nd: 3 dots
3rd: 5 dots
4th: 7 dots
Why are Class 6 Maths Chapter 1 Patterns in Mathematics question answers important?
In Class 6, Patterns in Mathematics is a very important chapter, and practising questions from this chapter is essential for scoring good marks in the exam. Class 6 Maths Patterns in Mathematics question answers help students in many ways.
- These structured NCERT solutions will help students understand all the important concepts related to this chapter.
- Understanding and visualising patterns in class 6 will build the foundation in reasoning, algebraic expressions, sequences, and functions in higher classes.
- These question answers will help to develop logical and analytical thinking.
NCERT Solutions for Class 6 Maths Chapter Wise
For students' preparation, Careers360 has gathered all NCERT Class 6 Maths Solutions here for quick and convenient access.
NCERT Books and NCERT Syllabus
To plan studies effectively, students should review the latest syllabus before the academic year starts. Find the updated syllabus links and recommended reference books below.
- NCERT Syllabus Class 6 Maths
- NCERT Books Class 6
- NCERT Books for Class 6 Maths
- NCERT Syllabus Class 6
Patterns in Mathematics is the starting chapter of class 6, and it will introduce students to various new concepts. These Class 6 Maths Patterns in Mathematics question answers discussed in this article are properly structured and will help students immensely during their practice. The Free downloadable PDF of the solutions will also help. All in all, this article can be a game-changer for students if they go through it thoroughly.
Frequently Asked Questions (FAQs)
Triangular numbers come from summing counting numbers (1, 1+2, 1+2+3…), while square numbers relate to adding consecutive triangular numbers. These patterns help the students build their logical thinking skills and tackle Class 6 Maths Chapter 1 Patterns in Mathematics question answers efficiently.
Yes, by practising diverse pattern-based questions, especially those with visual and logical steps, students can learn to quickly identify rules and improve their accuracy and problem-solving speed during exams.
The topics discussed in the NCERT Solutions for class 6 chapter 1 Patterns in Mathematics, are:
- Patterns in Numbers
- Visualising number sequences
- Relations among number sequences
- Patterns in shapes
- Relations to the number sequence
These solutions offer clear, step-by-step explanations, helping students understand sequence rules, solve number and shape pattern-related problems, and practice a variety of problems confidently.
Recognising patterns helps in real contexts like music rhythms, architectural designs, natural growth patterns, and mathematical problem-solving, enhancing analytical and predictive thinking.
If there is a set of numbers related to each other by a specific rule, then that rule is called a Pattern rule. For grade 6 maths, these patterns are relatively easy to understand. In higher classes, there will be challenging patterns to decode.
Yes. These NCERT Solutions for Class 6 Maths Chapter 1 are completely free for students, prepared carefully by subject matter experts at Careers360.
Recognising patterns helps in logical thinking, predicting sequences, and forming the base for higher mathematical concepts such as algebra and geometry.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters