NCERT Solutions for Class 6 Maths Chapter 3 - Number Play
Who says maths is boring? NCERT class 6 Maths chapter 3 Number Play will help us find patterns, solve puzzles, and use numbers to do playful thinking. We are all surrounded by numbers from all sides. If we carefully look around, we will find that a world of numbers surrounds us in a whole lot of new ways, from our class, height, weight, date of birth, the scores we obtain in any game, our ranks in a race, etc. Numbers organise and simplify our lives in many different ways and contexts. We have already gained the basic knowledge of mathematical operations and performed addition, subtraction, multiplication, and division on them to solve problems related to our daily lives. In Class 6 Maths chapter 3 solutions of Number Play, we continue this journey and deepen our understanding of numbers and their magical applications. We at Careers360 have designed this NCERT Solutions for Class 6 article to provide comprehensive, step-by-step solutions to the chapter's questions in a student-friendly format. Many toppers rely on NCERT Solutions because they are designed according to the latest syllabus.

The joy of math lies in patterns, puzzles, and playful thinking. Dealing with Class 6 Maths Chapter 1 Patterns in Mathematics question answer, students will learn some interesting topics such as Kaprekar’s magic number, the Collatz Conjecture, and Palindromic patterns. This chapter also focuses on mental math, Clock and calendar numbers, and how to plan winning strategies during a game. These NCERT Solutions for Class 6 Maths are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. Find everything you need—the Latest syllabus, revision notes, and practice PDFs—all in one place in this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 3 Number Play: Download PDF
Careers360 brings you Class 6 Maths Chapter 3 Number Play solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 3 Number Play
Given below are the detailed Class 6 Maths Chapter 3 Number Play question answers given in the textbook.
|
Number Play Class 6 Maths Chapter 3 Question Answers |
Question 1: Colour or mark the supercells in the table below.

Solution:

Question 2: Fill the table below with only 4-digit numbers such that the supercells are exactly the coloured cells.

Solution:

(Answers may vary)
Question 3: Fill the table below such that we get as many supercells as possible. Use numbers between 100 and 1000 without repetition.
Solution:

Question 4: Out of the 9 numbers, how many supercells are there in the table above?______________
Solution: As we can count from the table above, there are 5 supercells.
Question 5: Find out how many supercells are possible for different numbers of cells.
Do you notice any pattern? What is the method to fill a given table to get the maximum number of supercells? Explore and share your strategy.
Solution:
For ' n ' cells:
- If $\mathbf{n}$ is even, the maximum number of supercells is $\frac{\mathbf{n}}{2}$.
- If $\mathbf{n}$ is odd, the maximum number of supercells is $\frac{\mathbf{n + 1}}{\mathbf{2}}$.
For example:
| Number of cells (n) | Number of Supercells |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 2 |
Yes, there is a pattern in the number of supercells as described by the above formula.
Method to fill a given table to get the maximum number of supercells.
Step 1: Make the first cell a supercell. After that, each alternate cell is to be made a supercell.
Step 2: No consecutive cells can be supercell except in the case of 4 cells, because then the first and fourth cells can be supercell.
Question 6: Can you fill a supercell table without repeating numbers such that there are no supercells? Why or why not?
Solution: No, if we fill with numbers increasing by 1, we obtain at least one supercell, i.e., the last number.
Question 7: Will the cell having the largest number in a table always be a supercell? Can the cell having the smallest number in a table be a supercell? Why or why not?
Solution: Yes, the cell with the largest number in a table is always a supercell, while the cell with the smallest number will never be a supercell, as its adjacent cell has a bigger number.
Question 8: Fill a table such that the cell having the second largest number is not a supercell.
Solution:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
The second-to-last element is not the supercell. (Answers may vary)
Question 9: Fill a table such that the cell having the second-largest number is not a supercell, but the second-smallest number is a supercell. Is it possible?
Solution:
|
111 |
100 |
222 |
333 |
444 |
555 |
666 |
888 |
999 |
Here, 100 (the second smallest number) is a supercell, while 888 (the Second largest) is not a supercell.
∴ It is possible to make such cells. (Answers may vary)
Question 10: Make other variations of this puzzle and challenge your classmates.
Solution: Do It Yourself by taking different scenarios.
| Number Play Class 6 Chapter 3 Question Answers Page No.: 59 Number of Questions: 1 |
Question: Identify the numbers marked on the number lines below, and label the remaining positions.
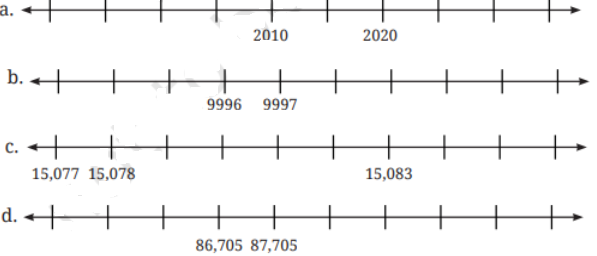
Put a circle around the smallest number and a box around the largest number in each of the sequences above.
Solution:




| Number Play Class 6 Chapter 3 Question Answers Page No.: 60 Number of Questions: 3 |
Question 1: Digit sum 14
a. Write other numbers whose digits add up to 14.
b. What is the smallest number whose digit sum is 14?
c. What is the largest 5-digit number whose digit sum is 14?
d. How big a number can you form having the digit sum of 14? Can you make an even bigger number?
Solution:
a. 95,59,86,68,923,.......... etc. (Answers may vary)
b. 59
c. 95000
d. 101010101010101010101010101,11111111111111,.......... so on.
Yes, we can make even bigger numbers.
Question 2: Find out the digit sums of all the numbers from 40 to 70. Share your observations with the class.
Solution:
| Number | Digit Sum | Number | Digit Sum | Number | Digit Sum |
| 40 | 4 | 51 | 6 | 62 | 8 |
| 41 | 5 | 52 | 7 | 63 | 9 |
| 42 | 6 | 53 | 8 | 64 | 10 |
| 43 | 7 | 54 | 9 | 65 | 11 |
| 44 | 8 | 55 | 10 | 66 | 12 |
| 45 | 9 | 56 | 11 | 67 | 13 |
| 46 | 10 | 57 | 12 | 68 | 14 |
| 47 | 11 | 58 | 13 | 69 | 15 |
| 48 | 12 | 59 | 14 | 70 | 7 |
| 49 | 13 | 60 | 6 | ||
| 50 | 5 | 61 | 7 |
Question 3: Calculate the digit sums of 3-digit numbers whose digits are consecutive (for example, 345). Do you see a pattern? Will this pattern continue?
Solution:
1+2+3=6
2+3+4=9
3+4+5=12
4+5+6=15
5+6+7=18
6+7+8=21
7+8+9=24
Yes, it follows the table of 3. We can’t continue this series after 789.
| Number Play Class 6 Chapter 3 Question Answers Page no.: 64-65 Number of Questions: 4 |
Question 1: Pratibha uses the digits ' 4 ', ' 7 ', ' 3 ' and ' 2 ', and makes the smallest and largest 4-digit numbers with them: 2347 and 7432. The difference between these two numbers is 7432−2347=5085. The sum of these two numbers is 9779. Choose 4 digits to make:
a. The difference between the largest and smallest numbers greater than 5085.
b. The difference between the largest and smallest numbers less than 5085.
c. The sum of the largest and smallest numbers greater than 9779.
d. The sum of the largest and smallest numbers less than 9779.
Solution:
a. Digits −8,7,3 and 2
Largest Number - 8732
Smallest Number - 2378
Difference =6354
6354>5085
b. Digits −1,2,3 and 4
Largest Number - 4321
Smallest Number - 1234
Difference =3087
c. Digits −9,8,7 and 6
Largest Number - 9876
Smallest Number - 6789
Sum =16665, which is greater than 9779.
d. Digits - 1, 2, 3, and 8
Largest Number 8321
Smallest Number 1238
Sum = 9559, which is less than 9779.
Question 2: What is the sum of the smallest and largest 5-digit palindromes? What is the difference?
Solution:
Smallest 5-digit palindrome number = 10001
Largest 5-digit palindrome number = 99999
Sum =10001+99999=110000
Difference = 99999−10001 =89998
Question 3: The time now is 10:01. How many minutes until the clock shows the next palindromic time? What about the one after that?
Solution: The Next palindromic time after 10:01 is 11:11, after 70 minutes. After that, the next palindromic time will be 12:21.
Question 4: How many rounds does the number 5683 take to reach the Kaprekar constant?
Solution:
Starting with 5683, arrange the digits in descending and ascending order. Subtract the smaller from the larger repeatedly:
8653 − 3568 = 5085
8550 − 0558 = 7992
9972 − 2799 = 6174.
It takes three rounds.
| Number Play Class 6 Chapter 3 Question Answers Page no.: 66 Number of Questions: 2 |
Question 1: Write an example for each of the scenarios below whenever possible.
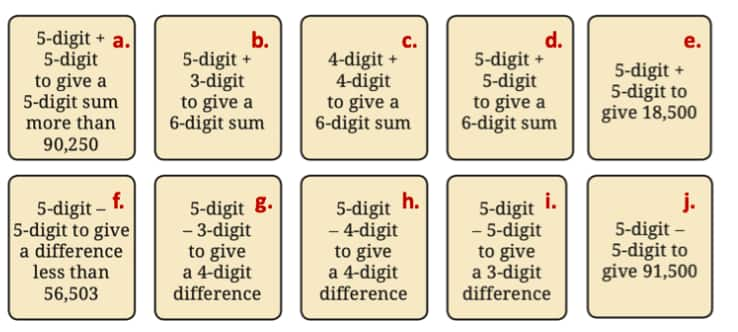
Could you find examples for all the cases? If not, think and discuss what could be the reason. Make other such questions and challenge your classmates.
Solution: Do it Yourself
{Hint: Answers may vary. See the hint and try some more examples
-
50000 + 30000 = 80000
-
99900 + 100 = 100000
-
9999 + 9999 = 19998. This is the biggest number that can be achieved by adding 4-digit numbers. So, there is no 6-digit number possible by the sum of two 4-digit numbers.
-
99999 + 10000 = 109999
-
30000 + (-11500) = 18500
-
65503 - 10000 = 55503
-
10000 - 999 = 9001
-
10000 - 1000 = 9000
-
99933 - 99000 = 933
-
81500 - (-10000) = 91500
Question 2: Always, Sometimes, Never?
Below are some statements. Think, explore, and find out if each of the statements is 'Always true', 'Only sometimes true' or 'Never true'. Why do you think so? Write your reasoning and discuss this with the class.
a. 5-digit number + 5-digit number gives a 5-digit number
b. 4-digit number + 2-digit number gives a 4-digit number
c. 4-digit number +2-digit number gives a 6 -digit number
d. 5-digit number-5-digit number gives a 5-digit number
e. 5-digit number-2-digit number gives a 3-digit number
Solution:
a. Only Sometimes [Example: 90000 + 10000=100000]
b. Only Sometimes[Example: 9999+10=10009]
c. That is never true, even if we took the largest four-digit number and the largest two-digit number.
Example: 9999 + 99 = 10098
d. Only Sometimes [Example: 99999-99000=999]
e. That is never true, even if we took the smallest five-digit number and the smallest two-digit number.
Example: 10000 - 99 = 9901
| Number Play Class 6 Chapter 3 Question Answers Page no.: 69-70 Number of Questions: 3 |
Question: We shall do some simple estimates. It is a fun exercise, and you may find it amusing to know the various numbers around us. Remember, we are not interested in the exact numbers for the following questions.
Share your methods of estimation with the class.
Question 1: Steps you would take to walk:
a. From the place you are sitting to the classroom door
b. Across the school ground from start to end
c. From your classroom door to the school gate
d. From your school to your home
Question 2: Number of times you blink your eyes or number of breaths you take:
a. In a minute
b. In an hour
c. In a day
Question 3: Name some objects around you that are:
a. a few thousand in number
b. more than ten thousand in number
Solution: (1,2,3): Complete the task yourself as per the given instructions.
| Number Play Class 6 Chapter 3 Question Answers Page no: 70-71 Number of Questions: 7 |
Try to guess within 30 seconds. Check your guess with your friends.
Question 1: Number of words in your maths textbook:
a. More than 5000
b. Less than 5000
Solution: a. More than 5000 (Number of words in a line multiplied by the number of lines in a page multiplied by the number of pages in the book)
Question 2: Number of students in your school who travel to school by bus:
a. More than 200
b. Less than 200
Solution: a. More than 200 (Number of seats multiplied by the number of students in one seat)
Question 3: Roshan wants to buy milk and 3 types of fruit to make fruit custard for 5 people. He estimates the cost to be ₹100. Do you agree with him? Why or why not?
Solution: No, because the milk will cost him somewhere between 25-35 Rupees, after that, the custard for 5 people will cost him more than 150 or more. Therefore, the amount is not sufficient.
Question 4: Estimate the distance between Gandhinagar (in Gujarat) to Kohima (in Nagaland).
Hint: Look at the map of India to locate these cities.
Solution: Gandhinagar (in Gujarat) is in the west of India, and Kohima (in Nagaland) is in the Northeast of India. Therefore, the approximate distance is 2500 km to 2800 km.
Question 5: Sheetal is in Grade 6 and says she has spent around 13,000 hours in school to date. Do you agree with her? Why or why not?
Solution: Yes, because on average, a student spends 8 hours a day in school. In an academic year, it is approximately equal to 2000 hours in each class. So, till class 6, a student spends more than 13000 hours.
Question 6: Earlier, people used to walk long distances as they had no other means of transport. Suppose you walk at your normal pace. Approximately, how long would it take you to go from:
a. Your current location to one of your favourite places nearby.
b. Your current location to any neighbouring state's capital city.
c. The southernmost point in India to the northernmost point in India.
Solution: Do it yourself
Question 7: Make some estimation questions and challenge your classmates!
Solution: Do it Yourself
| Number Play Class 6 Chapter 3 Question Answers Page No.: 72-73 Number of Questions: 10 |
Question 1: There is only one supercell (number greater than all its neighbours) in this grid. If you exchange two digits of one of the numbers, there will be 4 supercells. Figure out which digits to swap.
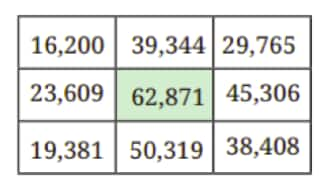
Solution:

Question 2: How many rounds does your year of birth take to reach the Kaprekar constant?
Solution:
Let your year of birth be 2009. Here's how the process looks:
- 2009 -> 9002 - 0029 = 8973
- 8973 -> 9873 - 3789 = 6084
- 6084 -> 8640 - 0468 = 8172
- 8172 -> 8721 - 1278 = 7443
- 7443 -> 7443 - 3447 = 3996
- 3996 -> 9963 - 3699 = 6264
- 6264 -> 6642 - 2466 = 4176
- 4176 -> 7614 - 1467 = 6147 (8 rounds)
Question 3: We are a group of 5-digit numbers between 35,000 and 75,000 such that all of our digits are odd. Who is the largest number in our group? Who is the smallest number in our group? Who among us is the closest to 50,000?
Solution: The possible odd digits are: 1,3,5,7, and 9.
-
Largest number: 73,999
-
Smallest number: 35,111
-
Closest to 50,000: 51,111
Question 4: Estimate the number of holidays you get in a year, including weekends, festivals and vacations. Then, try to get an exact number and see how close your estimate is.
Solution: Holidays in a year:
-
Weekends: 104 days
-
Summer vacation: 50 days
-
Winter vacation: 12 days
-
Festival holidays: 12 days
-
Public holidays: 4 days
Total estimated holidays =104+50+12+12+4=182 days.
Now compare this result with the calendar of the current year.
Question 5: Estimate the number of litres a mug, a bucket and an overhead tank can hold.
Solution: A mug can hold approximately 0.8 litres of water, whereas a bucket can hold 10 litres of water, and an overhead tank can hold 1000 litres of water.
Question 6: Write one 5-digit number and two 3-digit numbers such that their sum is 18,670.
Solution: The combination of a 5-digit number and two 3-digit numbers that add up to 18,670:
5-digit number: 12,345
3-digit number 1: 789
3-digit number 2: 536
Sum: 12,345+789+536=18,670
Question 7: Choose a number between 210 and 390. Create a number pattern similar to those shown in Section 3.9 that will sum up to this number.
Solution: We can create a simple addition pattern using a series of repeated numbers.
50+50+50+55+55+55+60=375
The pattern uses 50 repeated 3 times, 55 repeated 3 times and then a 60 to complete the sum.
50+50+50=150
55+55+55=165
150+165+60=375
Question 8: Recall the sequence of Powers of 2 from Chapter 1, Table 1. Why is the Collatz conjecture correct for all the starting numbers in this sequence?
Solution: The Collatz Conjecture and Powers of 2: The Collatz conjecture suggests that starting with any positive integer, repeatedly applying the following steps will eventually lead to the number 1:
If the number is even, divide it by 2.
If the number is odd, multiply it by 3 and add 1.
For powers of 2 (like 1, 2, 4, 8, 16, etc., as listed in Table 1 of Chapter 1), the Collatz conjecture holds because every power of 2 is even, so it always divides by 2.
Dividing powers of 2 by 2 continuously leads to smaller powers of 2, eventually reaching 1. This explains why the Collatz conjecture is correct for all starting numbers in the sequence of powers of 2.
Question 9: Check if the Collatz Conjecture holds for the starting number 100.
Solution: Checking: Applying the steps of the Collatz Conjecture to 100:
100 is even: 1002=50
50 is even: 502=25
25 is odd: 25×3+1=76
76 is even: 762=38
38 is even: 382=19
19 is odd: 19×3+1=58
58 is even: 582=29
29 is odd: 29×3+1=88
88 is even: 882=44
44 is even: 442=22
22 is even: 222=11
11 is odd: 11×3+1=34
34 is even: 342=17
17 is odd: 17×3+1=52
52 is even: 522=26
26 is even: 262=13
13 is odd: 13×3+1=40
40 is even: 402=20
20 is even: 202=10
10 is even: 102=5
5 is odd: 5×3+1=16
16 is even: 162=8
8 is even: 82=4
4 is even: 42=2
2 is even: 22=1
After these steps, we reach 1, confirming that the Collatz Conjecture holds for the starting number 100.
Question 10: Starting with 0, players alternate adding numbers between 1 and 3. The first person to reach 22 wins. What is the winning strategy now?
Solution:
The first player to reach 22 wins. So, 22 is a winning position.
-
If a player is at position 21, they can add 1 to reach 22, a winning position. Therefore, 21 is a losing position.
-
If a player is at position 20, they can add 2 to reach 22, a winning position. Therefore, 20 is a losing position.
-
If a player is at position 19, they can add 3 to reach 22, a winning position. Therefore, 19 is a losing position.
Thus, the positions 19, 20, and 21 are losing positions.
Continue working backwards in the same manner to identify the remaining losing and winning positions.
The winning strategy is to always force your opponent into one of the losing positions.
NCERT Solutions for Class 6 Maths Chapter 3 Number Play: Notes
Careers360 has prepared these Class 6 Number Play Notes to make your revision smoother and faster. Also, these notes will help students to understand the Number Play class 6 solutions and solve them on their own from next time.
Arrangement of Numbers
The numbers can be arranged in two ways, in ascending or descending order. If the numbers are arranged from smallest to largest, then they are in ascending order. If the numbers are arranged from largest to smallest, then it is in descending order.
For example,
Numbers: 3,7,8,9
Ascending order: 3,7,8,9
Descending order: 9,8,7,3
Supercells
A number is a supercell if it is greater than the adjacent numbers in the grid.
Observe the numbers written below. We observe that some numbers are coloured.
200 577 626 345 790 694 109 198
43 79 75 63 10 29 28 34
A cell is coloured if the number in it is larger than that of its adjacent cells. The number 626 is coloured as it is larger than 577 and 345, whereas 200 is not coloured as it is smaller than 577. The number 198 is coloured as it has only one adjacent cell with 109 in it, and 198 is larger than 109.
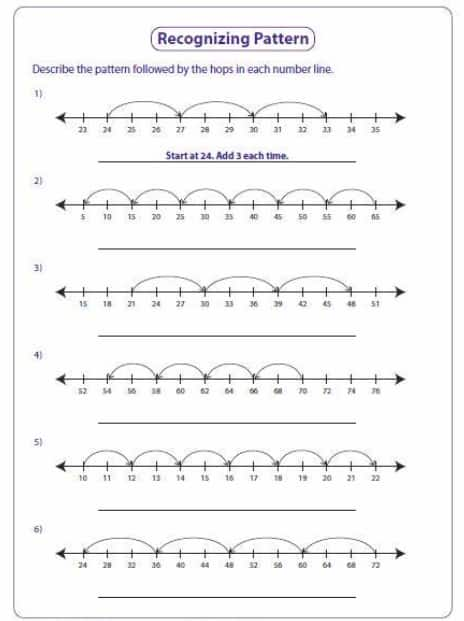
Patterns of Numbers on the Number Line
We can also formulate some patterns on the number line.
Digit sums of numbers
In certain numbers, the sum of their digits is the same.
For example, adding the digits of the number 68 will be the same as adding the digits of 176 or 545.
Pretty Palindromic Patterns
Palindromic numbers are numbers that remain the same when written or read from front to back or back to front.
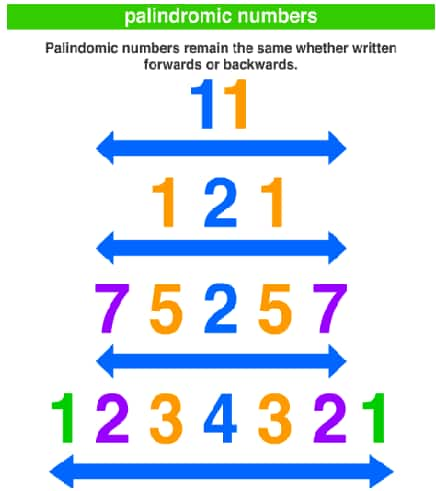
Let us consider a few numbers: 33, 848, 575, 454, 22, 88, etc. If we look carefully, we will surely figure out that these numbers read the same from left to right and from right to left.
Clock and Calendar Numbers
According to the chapter number play, on a 12-hour clock, certain times have interesting patterns, like 4:44, 10:10, and 12:21.
Examples
- Rekha's birthday is on 20/12/2012, where the digits ‘2’, ‘0’, ‘1’, and ‘2’ repeat in that order.
- Rahul's birthday is on 11/02/2011, where the digits read the same from left to right and from right to left.
An Unsolved Mystery — The Collatz Conjecture
As stated in the chapter on number play, the Collatz Conjecture is a famous unsolved problem in mathematics. The rule is simple:
- Start with any number.
- If the number is even, take half of it.
- If the number is odd, multiply it by 3 and add 1.
- Repeat.
Eventually, all sequences will reach the number 1, regardless of the whole number you start with.
For example, 21, 64, 32, 16, 8, 4, 2, 1
Number Play Class 6 Maths Chapter 3:Topics
Topics you will learn in NCERT Class 6 Maths Chapter 3 Number Play include:
3.1 Numbers can Tell us Things
3.2 Supercells
3.3 Patterns of Numbers on the Number Line
3.4 Playing with Digits
3.5 Pretty Palindromic Patterns
3.6 The Magic Number of Kaprekar
3.7 Clock and Calendar Numbers
3.8 Mental Math
3.9 Playing with Number Patterns
3.10 An Unsolved Mystery - the Collatz Conjecture!
3.11 Simple Estimation
3.12 Games and Winning Strategies
Class 6 Maths Chapter 3 Number Play solutions: Extra Question
Question:
In a game, players need to find numbers that are palindromes on the number line. A palindrome is a number that reads the same forwards and backwards. For example, 121 and 898 are palindromes.
List the first five palindrome numbers between 100 and 200.
Solution:
A palindrome number is a number that remains the same when its digits are reversed. Let’s list the palindromes between 100 and 200:
-
101 (reads the same forward and backwards)
-
111 (reads the same forward and backwards)
-
121 (reads the same forward and backwards)
-
131 (reads the same forward and backwards)
-
141 (reads the same forward and backwards)
So, the first five palindrome numbers between 100 and 200 are 101, 111, 121, 131, and 141.
NCERT Solutions for Class 6 Maths Chapter 3 Number Play: Points to Remember
These important points will help you solve Number Play NCERT solutions with greater efficiency.
Ascending order: The arrangement of numbers from low to high.
Descending order: The arrangement of numbers from high to low.
Supercells: A number is a supercell if it is greater than the adjacent numbers in the grid.
Palindromic numbers: Palindromic numbers are numbers that remain the same when written or read from front to back or back to front.
NCERT Solutions for Class 6 Maths Chapter Wise
Access all NCERT Class 6 Maths solutions from one place using the links below.
NCERT Books and Syllabus
Download some NCERT reference books and check the syllabus for Class 6 Maths from the links given below.
Frequently Asked Questions (FAQs)
Here are the topics covered in the NCERT Class 6 Maths Chapter 3.
- Numbers can tell us Things
- Supercells
- Patterns of numbers on the number line
- Playing with digits
- Palindromic patterns
- The Magic Number of Kaprekar
- Clock and calendar numbers
- Mental health
- Playing with number patterns
- The Collatz Conjecture
- Simple estimation
- Games and winning strategies
It is a famous mathematical puzzle:
Start with any positive integer.
If it's even, divide by 2.
If it's odd, multiply by 3 and add 1.
Repeat the steps. You’ll always end up at 1.It's simple, but it remains an unsolved problem as to whether Collatz’s conjecture is true or not. Collatz’s conjecture is one of the most famous unsolved problems in mathematics.
Here are the names of some books which will strengthen concepts related to Class 6 Chapter 3 Number Play.
- NCERT Mathematics Textbook – Class 6
- R.D. Sharma Class 6 Mathematics
- R.S. Aggarwal’s Mental Mathematics for Class 6
- Math Olympiad Workbooks
A palindrome is a number that reads the same forwards and backwards. Palindromic patterns help students explore symmetry in numbers.
Example: 121, 1331, etc
Kaprekar’s constant is a number with a unique property. When you rearrange the digits of any 4-digit number (with at least two different digits) to form the largest and smallest possible numbers and subtract them, repeating this process always leads to 6174. 6174 is regarded as Kaprekar's constant.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
