Search Colleges, Exams, Schools & more
Login
NCERT Solutions for Class 6 Maths Chapter 13 Symmetry
NCERT Solutions for Class 6 Maths Chapter 13 Symmetry are discussed in this article. These NCERT solutions are created by the expert team at careers360 considering the latest CBSE syllabus 2023. In this chapter, you will learn some basic Symmetry concepts like line symmetry, lines of symmetry for regular polygons, and rotational symmetry. In this article, you will get NCERT solutions for Class 6 Maths chapter 13 Symmetry where you get questions related to finding basic symmetry of some Mathematical geometry.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 13 Symmetry - Important Points
- NCERT Solutions for Class 6 Maths Chapter 13 Symmetry
- NCERT Solutions for Class 6 Maths Chapter 13 Symmetry (Intext Questions and Exercise)
- NCERT Class 6 Maths Chapter 13 Symmetry Exercise: 13.1
- NCERT for Class 6 Maths Chapter 13 Symmetry Exercise 13.2
- NCER Class 6 Maths Chapter 13 Symmetry Topic 13.5 Reflection and Symmetry
- NCERT Class 6 Maths Chapter 13 Symmetry Exercise 13.3
- Main Topics Of Symmetry Class 6 Chapter 13 are Listed Below:
- Making Symmetric Figures: Ink-blot Devils
- NCERT Solutions for Class 6 Mathematics Chapter Wise
- NCERT Solutions for Class 6 - Subject Wise
As per the NCERT Syllabus for Class 6 Maths, it is an important concept of the geometrical part used by designers, artists, architects, and everybody who is working with some kind of design. In NCERT solutions for Class 6 Maths chapter 13 Symmetry , you will get questions related to different lines of symmetry such as a single line of symmetry, two lines of symmetry, three lines of symmetry or multiple lines of symmetry in NCERT. There are 17 questions in 3 exercises of this chapter from NCERT Books for Class 6 Maths. You will get detailed explanations of all these questions in the NCERT Solutions for Class 6. You will get the conceptual clarity of line of symmetry once you go through these solutions.
NCERT Solutions for Class 6 Maths Chapter 13 Symmetry - Important Points
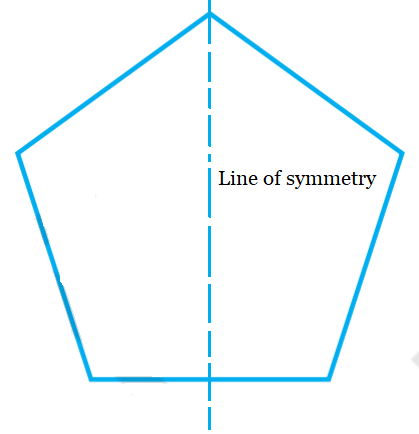
Line Symmetry: Line symmetry refers to a property of a figure where a line can be drawn to divide the figure into two identical or mirror-image parts. This line is called a line of symmetry. If a figure has line symmetry, it means that one part of the figure can be mapped onto the other part by a reflection across the line of symmetry.
Number of Lines of Symmetry: A figure may have different numbers of lines of symmetry, including:
- No line of symmetry: Some figures, like a scalene triangle, do not have any lines of symmetry. This means that they cannot be divided into two identical parts by any line.
- Only one line of symmetry: Figures such as an isosceles triangle have one line of symmetry. This line divides the figure into two mirror-image parts.
- Two lines of symmetry: A rectangle has two lines of symmetry. These lines divide the rectangle into four congruent parts.
- Three lines of symmetry: An equilateral triangle has three lines of symmetry. Each line divides the triangle into two mirror-image parts.
For more, Download Ebook - NCERT Class 6 Maths: Chapterwise Important Formulas And Points
Mirror Reflection and Left ↔ Right Changes: Line symmetry is closely related to mirror reflection. When we talk about mirror reflection, we consider the reversal or flipping of the figure across the mirror line. It involves changes in orientation, where the left side of the figure is transformed into the right side and vice versa.
Symmetry in Everyday Life: Symmetry has various applications in different aspects of everyday life, including:
- Art and Design: Symmetry is widely used in art, design, and architecture to create aesthetically pleasing and balanced compositions.
- Textile Technology: Symmetry plays a role in textile patterns and designs, where repeated symmetric motifs are often used.
- Geometrical Reasoning: Symmetry helps in geometric reasoning and understanding the properties of shapes and figures.
- Cultural Practices: Symmetry is prevalent in cultural practices like Kolams and Rangoli, where intricate patterns are created using symmetric designs.
Free Download NCERT Solutions for Class 6 Maths Chapter 13 Symmetry For CBSE Exam
NCERT Solutions for Class 6 Maths Chapter 13 Symmetry
NCERT Solutions for Class 6 Maths Chapter 13 Symmetry (Intext Questions and Exercise)
NCERT Class 6 Maths Chapter 13 Symmetry Exercise: 13.1
Question: 1 List any four symmetrical objects from your home or school.
Answer: Examples of symmetrical objects that we use in our home or school are as follows:
Book, DVD, spectacles, compass, etc.
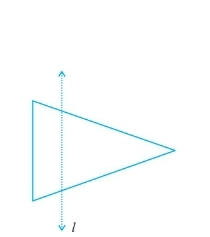
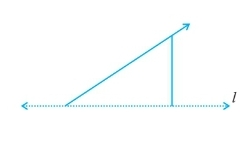
Question: 2 For the given figure, which one is the mirror line l1 or l2 ?
Answer: From the figure, we can say that line l2 is the mirror line.
Because, when the figure is completely folded about the line l2 then the left part is covered by the right part completely.
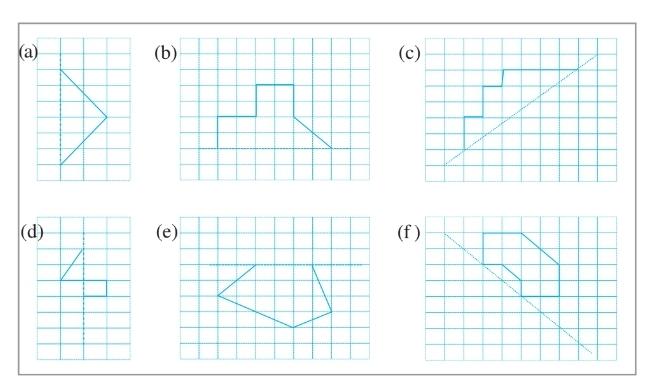
Question: 3 Identify the shapes given below. Check whether they are symmetric or not. Draw the line of symmetry as well.
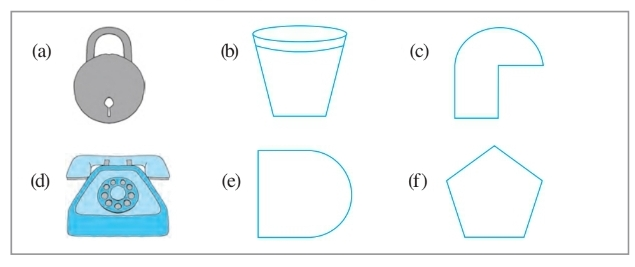
Answer: (a) Yes, it is symmetrical.
And the line of symmetry is shown in the figure.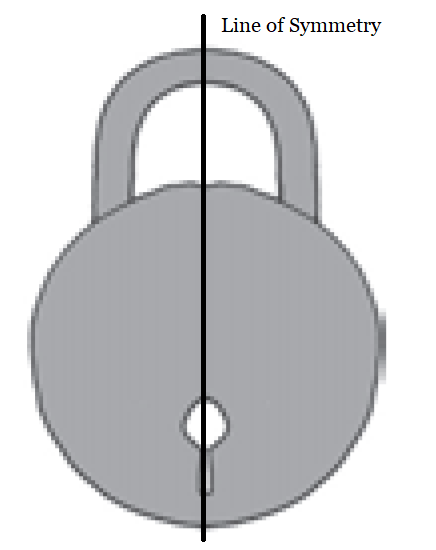 
(b) Yes, it is symmetrical.
And the line of symmetry is shown in the figure.
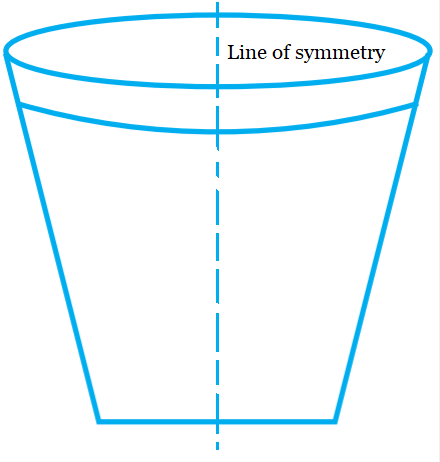
(c) No , it is not symmetrical hence there is no line of symmetry in it.
(d) Yes, it is symmetrical.
And the line of symmetry is shown in the figure.
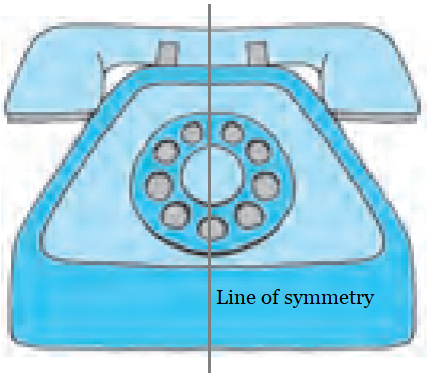
(e) Yes, it is symmetrical.
And the line of symmetry is shown in the figure.
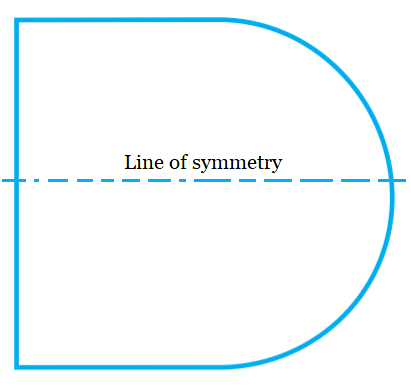
(f) Yes, it is symmetrical.
And the line of symmetry is shown in the figure.
Answer: After the completion of the above-given figures, we obtain the following figures.
(a)
(b)
(c)
(d)
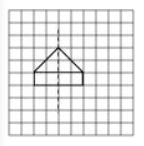
(e)
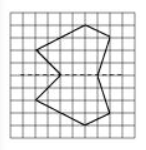
(f)
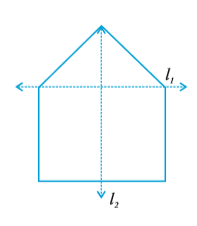
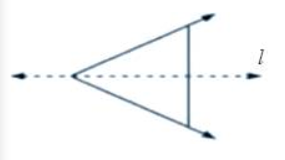
Question: 5 In the figure, l is the line of symmetry. Complete the diagram to make it symmetric.
Answer: The given figure can be completed as follows:
Answer: The above diagram can be completed as follows:
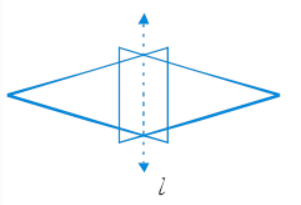
NCERT for Class 6 Maths Chapter 13 Symmetry Exercise 13.2
Question: 1 Find the number of lines of symmetry for each of the following shapes :
Answer: The number of lines of symmetry for each of the following shapes is given:
The number of lines of symmetry for each of the following shapes is given:
(a)
The given figure has 4 lines of symmetry
(b) .
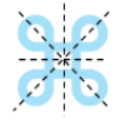
The given figure has 4 lines of symmetry.
(c)
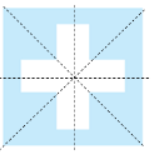
The given figure has 4 lines of symmetry
(d)
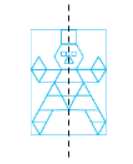
The given figure has only 1 line of symmetry.
(e)
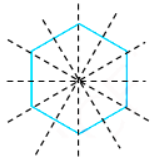
The given figure has 6 lines of symmetry.
(f)
The given figure has 6 lines of symmetry.
(g)
The given figure is asymmetrical and thus, there is no line of symmetry.
(h)
The given figure is asymmetrical and thus, there is no line of symmetry.
(i)
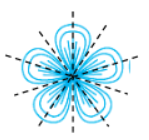
The given figure has 5 lines of symmetry.
Answer:
(a) The line of symmetry of the given figure:
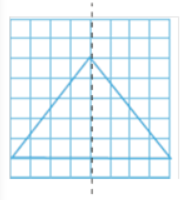
There is only one line of symmetry therefore, it is an isosceles triangle.
(b) The line of symmetry of the given figure:
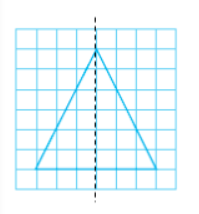
There is only one line of symmetry therefore, it is an isosceles triangle.
(c) The line of symmetry of the given figure:
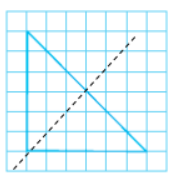
There is only one line of symmetry and an angle is right-angled therefore, it is a right-angled isosceles triangle.
(d) The line of symmetry of the given figure:
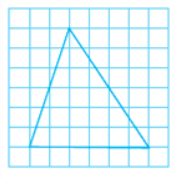
There is no line of symmetry therefore, it is a scalene triangle.
Question:3 Complete the following table.
Shape | Rough figure | Number of lines of symmetry |
Equilateral triangle | 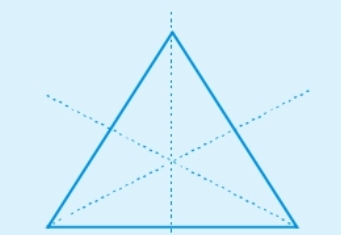 | 3 |
Square | ||
| Rectangle | ||
Isosceles triangle | ||
Rhombus | ||
| Circle |
Answer: The completed table is shown below:
| Shape | Rough Figure | No. of lines of symmetry |
| Equilateral triangle | 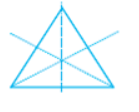 | 3 |
| Square | 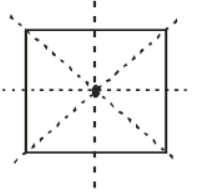 | 4 |
| Rectangle | 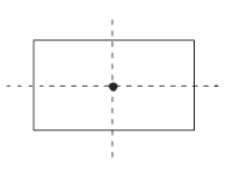 | 2 |
| Isosceles Triangle | 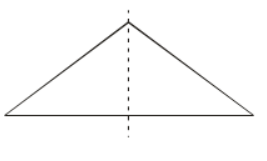 | 1 |
| Rhombus | 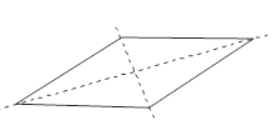 | 2 |
| Circle | 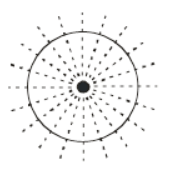 | Infinite or countless |
Question: 4 Can you draw a triangle which has
(a) exactly one line of symmetry?
(b) exactly two lines of symmetry?
(c) exactly three lines of symmetry?
(d) no lines of symmetry?
Sketch a rough figure in each case.
Answer:
(a) Yes, with one line of symmetry we have the triangle:
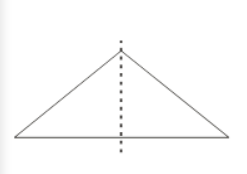
This is an isosceles triangle.
(b) No, as there exists no triangle with only two symmetry lines.
Hence, no such triangle is possible.
(c) Yes, a triangle with three lines of symmetry is possible:
And it is an equilateral triangle, shown below in the figure.
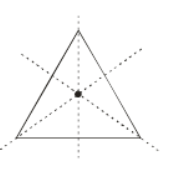
(d) Yes, the triangle with no line of symmetry is possible and it is a scalene triangle:
Shown below,
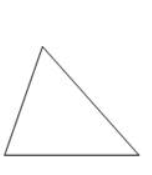
Question: 5 On a squared paper, sketch the following:
(a) A triangle with a horizontal line of symmetry but no vertical line of symmetry.
(b) A quadrilateral with both horizontal and vertical lines of symmetry.
(c) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(d) A hexagon with exactly two lines of symmetry.
(e) A hexagon with six lines of symmetry.
( Hint: It will be helpful if you first draw the lines of symmetry and then complete the figures.)
Answer:
(a) Triangle with only one line of symmetry is the horizontal line of symmetry and no vertical line of symmetry.
Hence, for the given case,
The triangle can be drawn as:
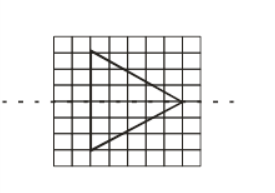
(b) The quadrilateral which has both the horizontal line and the vertical line of symmetry.
Hence, for the given case:
The quadrilateral can be drawn as:
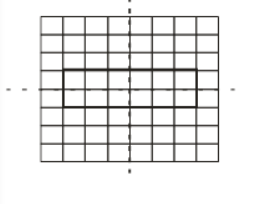
(c) The quadrilateral which has only one line of symmetry that is:
The horizontal line of symmetry and No, vertical line of symmetry.
Hence, for the given case we have:
The quadrilateral can be drawn as:
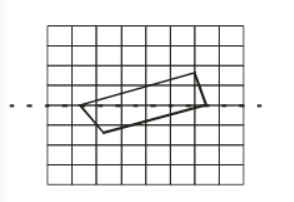
(d) The hexagon which has exactly two lines of symmetry that is:
The horizontal line of symmetry and the vertical line of symmetry.
Hence, for the given case, we have the hexagon can be drawn as:
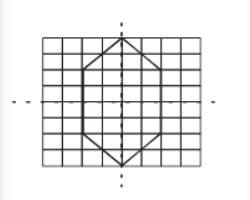
(e) The hexagon has all six lines of symmetry.
First, draw the six lines of symmetry and then complete the hexagon.
Hence, for the given case,
The hexagon can be drawn as:
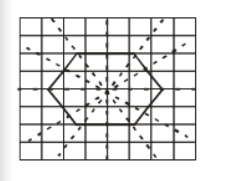
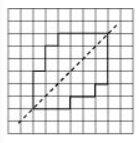
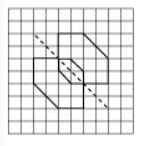
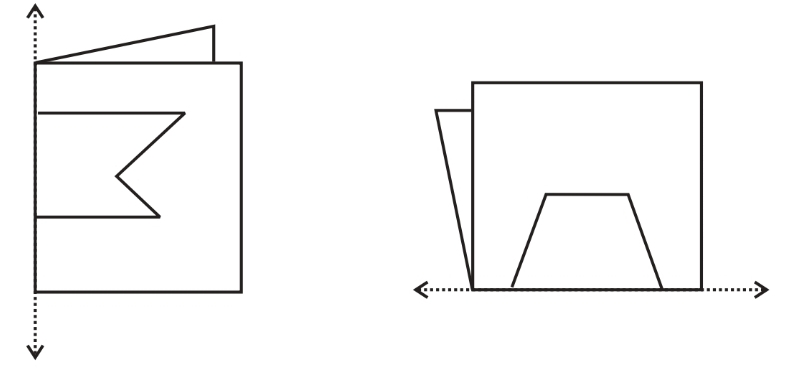
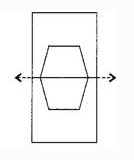
Question: 6 Trace each figure and draw the lines of symmetry if any:
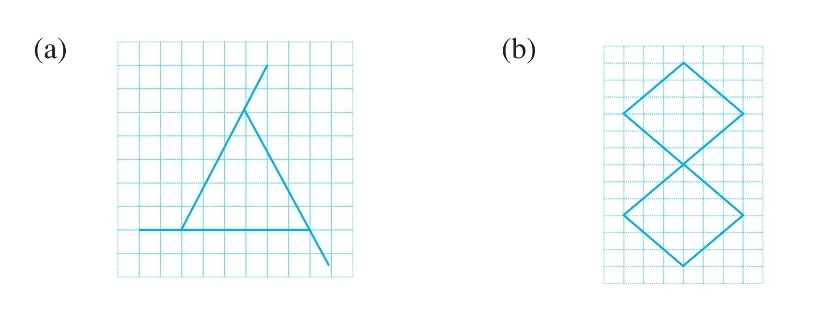
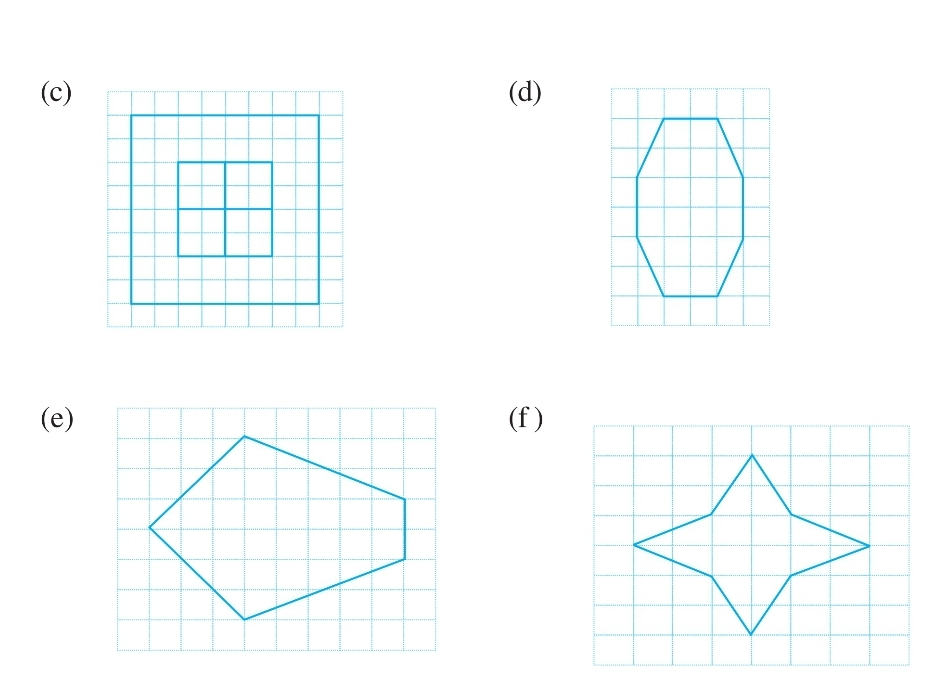
Answer:
(a) The given figure is asymmetrical. Hence, there is no possibility of the line of symmetry.
(b) By observation, the given figure has two squares having a common vertex.
Hence, there are two lines of symmetry possible.
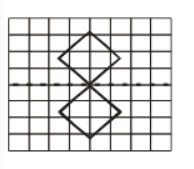
(c) By observation, the given figure has two squares with a common centre.
Hence, the given figure will have four lines of symmetry.
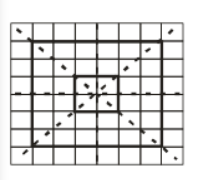
(d) By observation, the given is octagonal.
Hence, it will have two lines of symmetry.
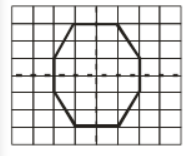
(e) By observation, the given figure is not any specific.
Hence, It will have only one line of symmetry.
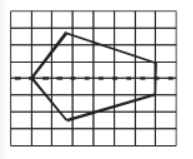
(f) Here, we can observe that the given figure is a four-cornered figure.
Hence, it will have four lines of symmetry.
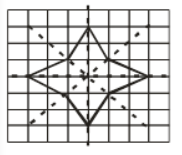
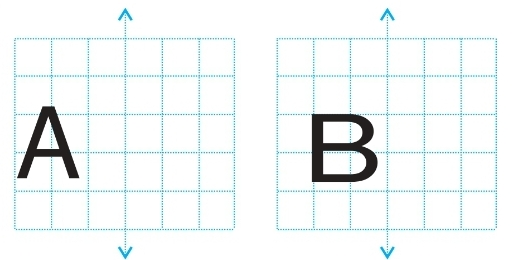
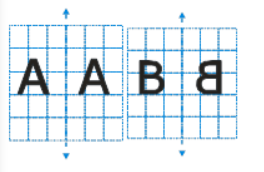
Question: 7 Consider the letters of English alphabets, A to Z. List among them the letters which have
(a) vertical lines of symmetry (like A)
(b) horizontal lines of symmetry (like B)
(c) no lines of symmetry (like Q)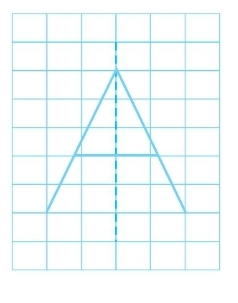 
Answer: (a) The letters having the vertical line of symmetry are as follows:
A, H, I, M, O, T, U, V, W, X, Y
(b) The letters having the horizontal line of symmetry are as follows:
B, C, D, E, H, I, K, O, X
(c) The letters that have no line of symmetry are as follows:
F, G, J, L, N, P, Q, R, S, Z
Answer:
By observation we can complete the given figure as follows:
NCER Class 6 Maths Chapter 13 Symmetry Topic 13.5 Reflection and Symmetry
Answer: The image appears to be 200 cm away from us, i.e., 100 cm on the other of the mirror.
And if we move towards the mirror, the image moves closer to us and to the mirror, but the size remains the same.
NCERT Class 6 Maths Chapter 13 Symmetry Exercise 13.3
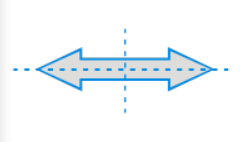
Question: 1 Find the number of lines of symmetry in each of the following shapes. How will you check your answers?
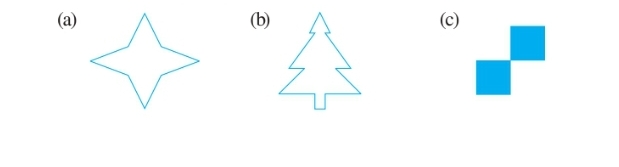
Answer:
(a) From the given figure, we can observe that,
There are 4 lines of symmetry in the given figure and the lines of symmetry can be shown as:
(b) From the given figure, we can observe that,
There is only 1 line of symmetry in the given figure and it can be drawn as follows:
(c) From the given figure, we can observe that,
There are two lines of symmetry in the given figure and it can be drawn as follows:
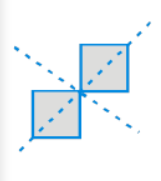
(d) From the given figure, we can observe that,
There are two lines of symmetry and it can be drawn as follows:
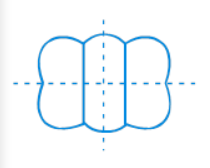
(e) From the given figure, we can observe that,
There is only one line of symmetry possible and it can be drawn as follows:
(f) From the given figure, we can observe that,
There are 2 lines of symmetry possible in the given figure and it can be drawn as follows:
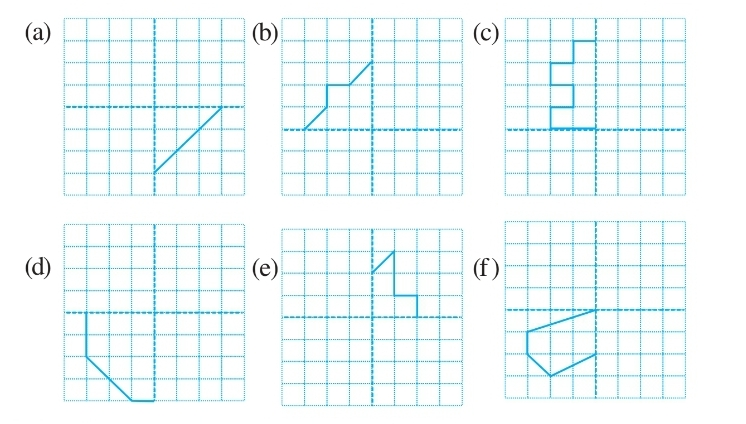
How did you go about completing the picture?
Answer:
(a) The given figure can be completed with the help of two symmetric lines i.e., horizontal and vertical lines of symmetry.
Therefore, the completed figure is shown as follows:
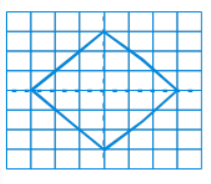
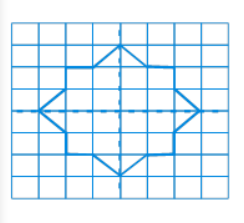
(b) We can complete the figure with the help of horizontal and vertical lines of symmetry.
Therefore, the above-given figure can be completed as follows:
(c) The given figure can be completed with the help of horizontal and vertical lines of symmetry.
Therefore, the completed figure is shown below:
(d) The given figure can be completed with the help of horizontal and vertical lines of symmetry.
Therefore, the completed figure is shown below:
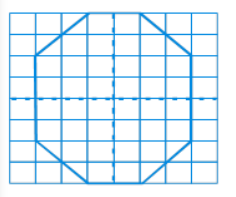
(e) The same parts can be drawn to complete the given figure with the help of horizontal and vertical lines of symmetry.
Therefore, the completed figure is shown below:
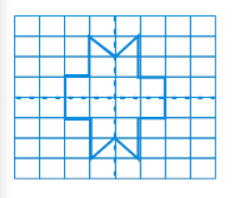
(f) The same parts can be drawn to complete the given figure with the help of horizontal and vertical lines of symmetry.
Therefore, the completed figure is shown below:
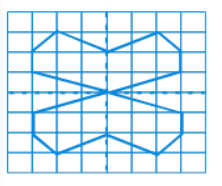
Try for OEMNPHLTSVX
Answer:
Mirror images for the given figures are shown as follows:
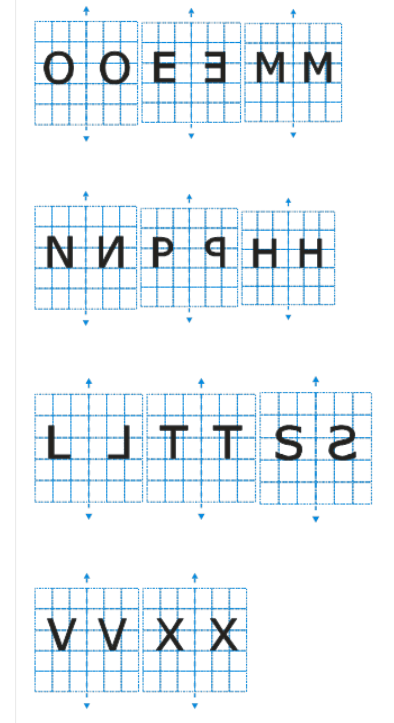
So, from the above-drawn figures, we can say that the figures having the vertical line of symmetry will have the same mirror images and the letters are:
O, M, H, T, V, X
Thus, the mirror images of these letters will look the same.
Main Topics Of Symmetry Class 6 Chapter 13 are Listed Below:
Making Symmetric Figures: Ink-blot Devils
NCERT Solutions for Class 6 Maths Chapter 13 Symmetry - Summary
In nature tree leaves, humans, animals, beehives, flowers, and in the religious logo and symbols you can find various types of symmetrical designs. Symmetry means that one shape becomes exactly like another when you turn, flip or slide it in some way. If any object or figure can be divided into two identical parts by a virtual line it has a line of symmetry. For example, If you cut the image of a human vertically through the middle of the head then both half will be the same. So you can say that human has a single line of symmetry. In Class 7 you will study the rotional symmetry and the order of symmetry. A scalene triangle (all three sides have different lengths) has no line of symmetry, an isosceles triangle has only one line of symmetry, a rectangle has two lines of symmetry and an equilateral triangle has three lines of symmetry. You can get NCERT Solutions from Class 6 to 12 to learn science and maths by clicking given in this article.
Also Check
NCERT Books and NCERT Syllabus
NCERT Solutions for Class 6 Mathematics Chapter Wise
| Chapters No. | Chapters Name |
| Chapter - 1 | Knowing Our Numbers |
| Chapter - 2 | Whole Numbers |
| Chapter - 3 | Playing with Numbers |
| Chapter - 4 | Basic Geometrical Ideas |
| Chapter - 5 | Understanding Elementary Shapes |
| Chapter - 6 | Integers |
| Chapter - 7 | Fractions |
| Chapter - 8 | Decimals |
| Chapter - 9 | Data Handling |
| Chapter -10 | Mensuration |
| Chapter -11 | Algebra |
| Chapter -12 | Ratio and Proportion |
| Chapter -13 | Symmetry |
| Chapter -14 | Practical Geometry |
NCERT Solutions for Class 6 - Subject Wise
Benefits of NCERT solutions for class 6 maths chapter 13 symmetry-
- You will learn solutions of NCERT for Class 6 easily.
- You will get many questions related to line of symmetry which will give more clarity.
- In NCERT Solutions for Class 6 Maths chapter 13 Symmetry, you will get all these questions related to line of symmetry explained with the help of figures. So it will help you to visualize the problem and understand it better.
- It is going to help you with your homework as all the practice questions given below every topic are also covered in this solution article.
Happy learning!!!
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters