NCERT Solutions for Class 6 Maths Chapter 2 - Lines and Angles
Lines and angles are the building blocks of geometry, helping us make different shapes. Lines and angles are everywhere, all around us, from the straight road we take to the corners of our room that we live in. These fundamental concepts of geometry help us understand the real use of mathematics in our daily lives. In Chapter 2 of Class 6 Maths, Lines and Angles, we will learn about concepts such as points, rays, line segments, lines, angles, etc. This article about NCERT Solutions for Class 6 Maths contains solutions to all the questions in this chapter of the NCERT Class 6 Maths Book. Many toppers rely on NCERT Solutions because they are designed according to the latest syllabus.
This Story also Contains
- NCERT Solutions for Class 6 Maths Chapter 2 Lines and Angles: Download PDF
- NCERT Solutions for Class 6 Maths Chapter 2 Lines and Angles (Exercise)
- NCERT Class 6 Maths Chapter 2 Solutions: Topics
- Class 6 Maths Chapter 2 Lines and Angles solutions: Extra Question
- Class 6 Maths Chapter 2 Lines and Angles solutions: Important Notes
- Lines and Angles Class 6 NCERT Solutions: Points to Remember
- NCERT Solutions for Class 6 Maths Chapter Wise
- NCERT Books and the NCERT Syllabus

Mastering lines and angles makes every shape around us easier to understand. These Lines and Angles Class 6 NCERT Solutions provide step-by-step explanations that help students build a strong foundation in maths with proper conceptual clarity. These NCERT Solutions are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. NCERT Solutions for class 6 are very helpful for the students during exam preparation to practice more questions and help them face the questions with confidence. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 6 Maths Chapter 2 Lines and Angles: Download PDF
Careers360 brings you NCERT Solutions for Class 6 Maths Chapter 2, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 6 Maths Chapter 2 Lines and Angles (Exercise)
Given below are the detailed Class 6 Maths Chapter 2 Lines and Angles question answers given in the textbook.
|
Page number: 15-17 Question: 6 |
Question 1:

Can you help Rihan and Sheetal find their answers?
Answer: Rihan can draw an infinite number of lines that pass through the point, whereas Sheetal can draw only one line that passes through both of the points.
Question 2: Name the line segments in Fig. 2.4. Which of the five marked points are on exactly one of the line segments? Which are on two of the line segments?
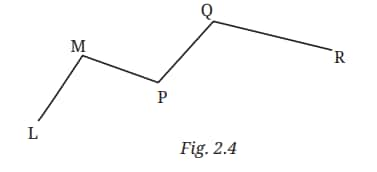
Answer: In the given figure, there are four line segments, i.e., $\overline{\mathrm{LM}}, \overline{\mathrm{MP}}, \overline{\mathrm{PQ}}, \overline{\mathrm{QR}}$
Points $L$ and $R$ are on one of the line segments.
Points $M$, $P$, and $Q$ are on two of the line segments.
Question 3: Name the rays shown in Fig. 2.5. Is T the starting point of each of these rays?
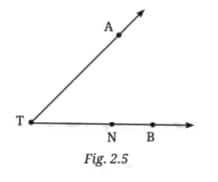
Answer:
In the given figure, there are two rays:
-
Ray TA: This ray starts at point T and passes through point A, extending infinitely beyond A.
-
Ray TB: This ray also starts at point T and passes through point B, extending infinitely beyond B.
So yes, T is the starting point of both rays.
Question 4: Draw a rough figure and write labels appropriately to illustrate each of the following: a. OP and OQ meet at O. b. XY and PQ intersect at point M. c. Line l contains points E and F but not point D. d. Point P lies on AB.
Answer:
a. OP and OQ meet at O
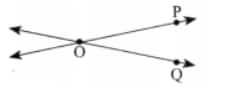
b. XY and PQ intersect at point M
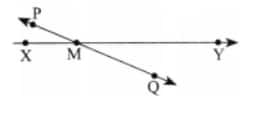
c. Line l contains points E and F but not point D
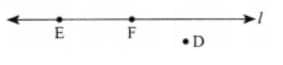
d. Point P lies on AB.

Question 5: In Fig. 2.6, name:
a. Five points
b. A line
c. Four rays
d. Five line segments
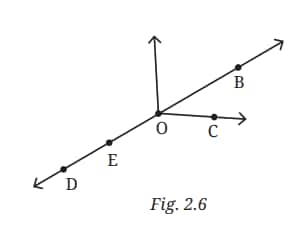
Answer:
(a) Five points are: B, C, D, E, and O
(b) A line is: DB (or BD)
(c) Four rays are: OB, OC, OD, and OE
(d) Five line segments are: OB, OC, OD, DE, and OE.
Question 6: Here is a ray $\overrightarrow{OA}$ (Fig. 2.7). It starts at O and passes through the point A. It also passes through point B.
a. Can you also name it as $\overrightarrow{OB}$? Why?
b. Can we write $\overrightarrow{OA}$ as $\overrightarrow{AO}$? Why or why not?
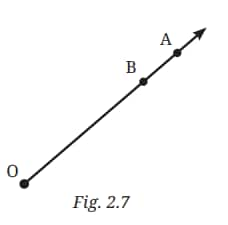
Answer:
a) Yes, the ray can also be named $\overrightarrow{OB}$ because the ray $\overrightarrow{OA}$ passes through point B as well. Rays are named starting from the initial point and passing through any other point on the ray. Since the ray starts at O and passes through both B and A, it can be named $\overrightarrow{OB}$.
b) No, we cannot write $\overrightarrow{OA}$ as $\overrightarrow{AO}$ because rays are directional. The ray starts at point 0 and extends through A, so $\overrightarrow{OA}$ indicates the direction from 0 to A. Writing it as $\overrightarrow{AO}$ would imply the ray starts at A and goes towards 0, which is incorrect in this context because 0 is the starting point.
|
Lines and Angles Class 6 Questions and Answers Page number: 19-21 Question: 6 |
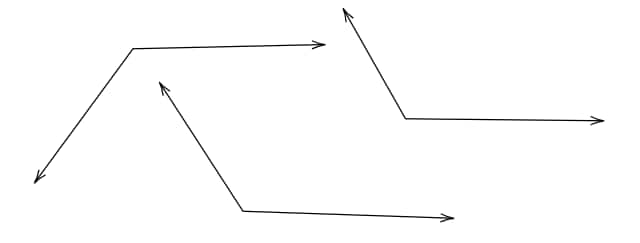
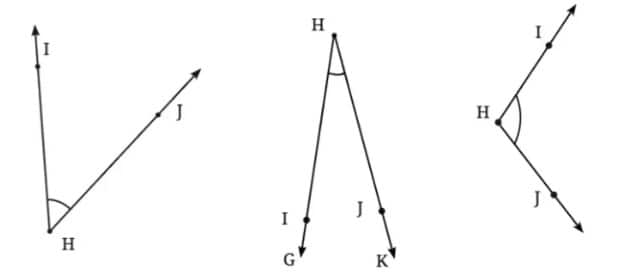
Question 1: Can you find the angles in the given pictures? Draw the rays forming any one of the angles and name the vertex of the angle.
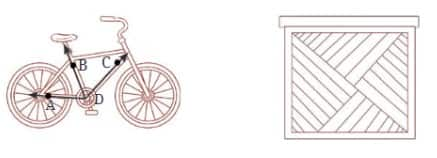

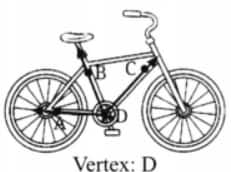
Answer:
The name of the vertex of ∠BDC is D.
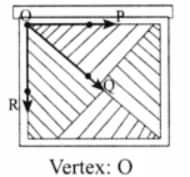
The name of the vertex of ∠POR is O.
The name of the vertex of ∠LKM is K.

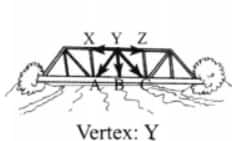
The name of the vertex of ∠AYC is Y.
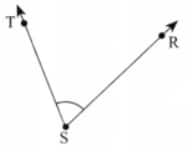
Question 2: Draw and label an angle with arms ST and SR.
Answer: We can draw an angle ∠RST of any measure with vertex $S$ and arms $\overrightarrow{ST}$ and $\overrightarrow{SR}$.
Question 3: Explain why ∠APC cannot be labelled as ∠P

Answer: Using a single letter name like ∠P is insufficient in case of two or more angles having the same vertex. Here, ∠P can be considered for any of the three angles ∠APB,∠BPC or ∠APC. So, here it is necessary to use three letters in specifying an angle.
Question 4: Name the angles marked in the given figure.
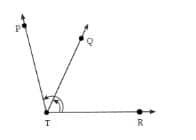
Answer: In the given figure, two angles have been marked with a common arm $\overrightarrow{TR}$. We can name these angles as ∠RTQ and ∠RTP or ∠PTR and ∠QTR.
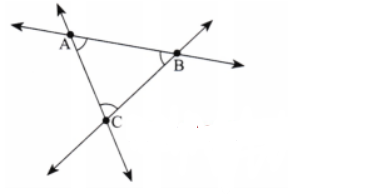
Question 5: Mark any three points on your paper that are not on one line. Label them A, B, and C. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C? Write them down, and mark each of them with a curve as in Fig. 2.9.
Answer: We get three lines $\overleftrightarrow{AB}$, $\overleftrightarrow{BC}$, and $\overleftrightarrow{CA}$ by joining pairs of these points. There are three angles, ∠ABC, ∠ACB, and ∠BAC, formed using these points.
Question 6: Now mark any four points on your paper so that no three of them are on one line. Label them A, B, C, D. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C, D? Write them all down, and mark each of them with a curve as in Fig. 2.9.
Answer: We can draw the figure as shown below. We get 6 lines in all. These are $\overrightarrow{AB}$, $\overrightarrow{BC}$, $\overrightarrow{CD}$, $\overrightarrow{CD}$, $\overrightarrow{AC}$, $\overrightarrow{BD}$.
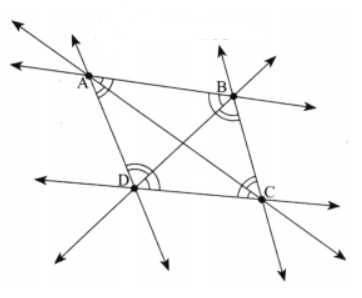
We get 12 angles in all. These are ∠ABC, ∠ABD, ∠GBD; ∠BCD, ∠BCA, ∠ACD; ∠CDA, ∠CDB, ∠BDA; ∠DAB, ∠DAC, and ∠CAB.
|
Lines and Angles Class 6 Questions and Answers Page number: 23 Question: 3 |
Question 1: Fold a rectangular sheet of paper, then draw a line along the fold created. Name and compare the angles formed between the fold and the sides of the paper. Make different angles by folding a rectangular sheet of paper and compare the angles. Which is the largest and smallest angle you made?

Answer:
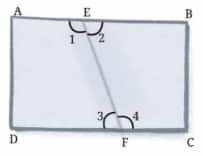
The angles formed with a line along the fold created are ∠AEF, ∠BEF,∠DFE, and ∠CFE, which are marked with 1, 2, 3, and 4. Out of these angles ∠AEF and ∠CFE are the larger ones, whereas ∠BEF and ∠DFE are the smaller ones.
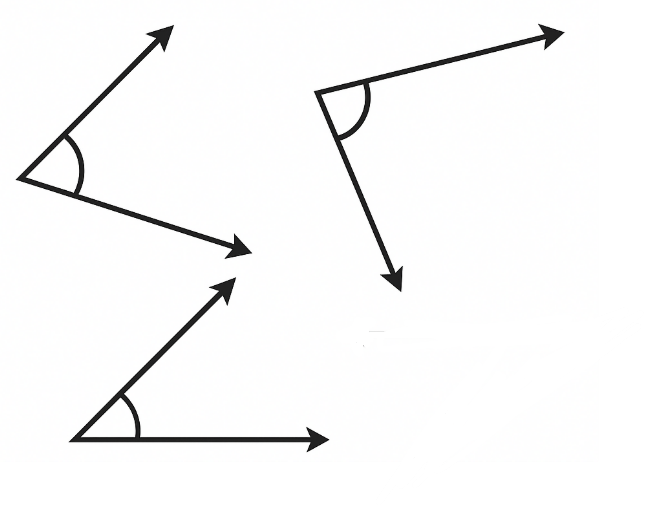
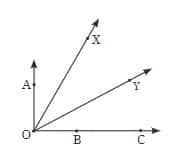
Question 2: In each case, determine which angle is greater and why. a. ∠AOB or ∠XOY b. ∠AOB or ∠XOB c. ∠XOB or ∠XOC Discuss with your friends on how you decided which one is greater.
Answer:
(a) ∠AOB>∠XOY because ∠XOY lies in the interior of ∠AOB.
(b) ∠AOB>∠XOB because both angles have one arm, OB common, but the uncommon arm OX of ∠XOB lies in the interior of ∠AOB.
(c) ∠XOB =∠XOC because OB and OC both denote the same ray, so both angles have the common arms and the same vertex. That is, they superimpose on each other.
Question 3: Which angle is greater: ∠XOY or ∠AOB? Give reasons.
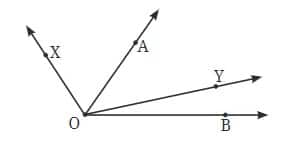
Answer:
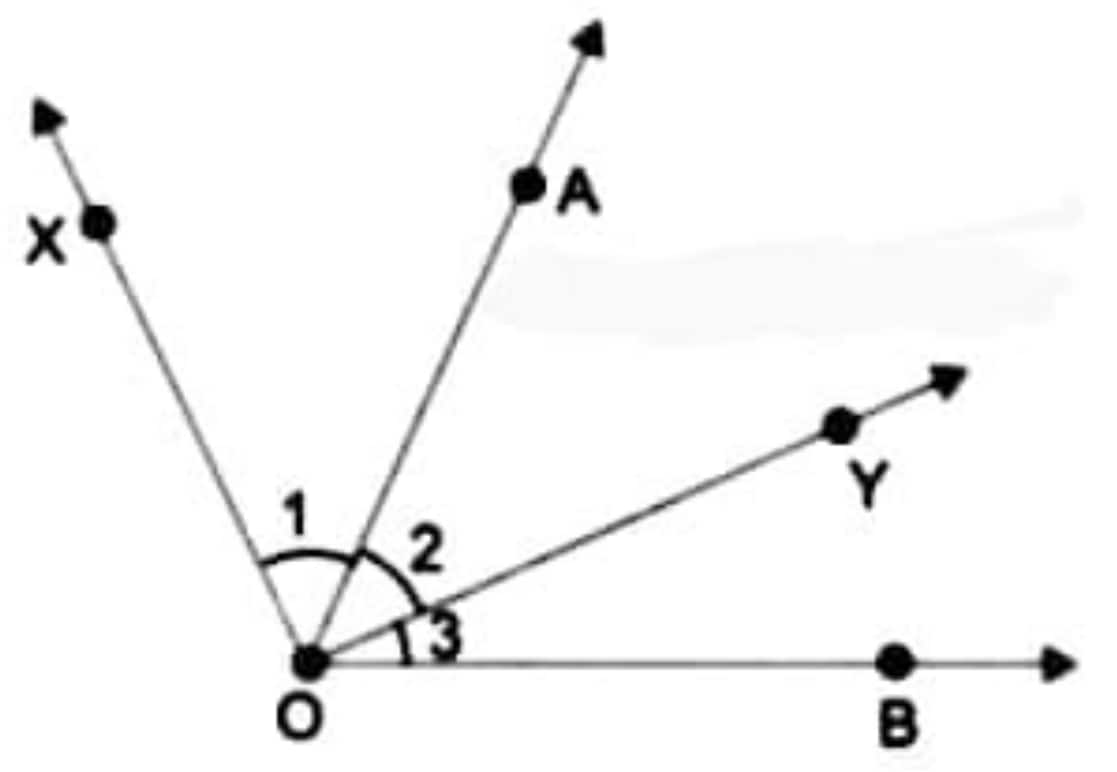
∠1 > ∠3 (∠1 has more spread than ∠3)
∠1 + ∠2 > ∠3 + ∠2 (adding ∠2 to both sides)
Hence, ∠XOY > ∠AOB
|
Lines and Angles Class 6 Questions and Answers Page number: 29-31 Question: 4 |
Question 1: How many right angles do the windows of your classroom contain? Do you see other right angles in your classroom?
Answer: In my classroom, the windows typically contain several right angles, as the corners where the frames meet are usually 90 degrees. Every rectangular or square-shaped window has four right angles.
Besides windows, other objects in the classroom with right angles include the corners of the doors, the edges of the blackboard or whiteboard, the desks or tables, and tiles on the floor or walls, which may also contain right angles as they are square and rectangular.
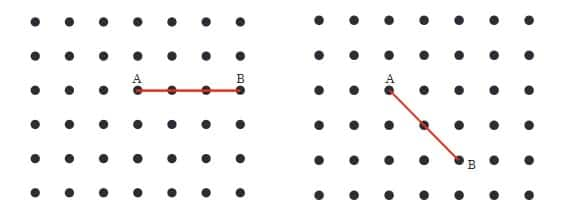
Question 2: Join A to other grid points in the figure by a straight line to get a straight angle. What are all the different ways of doing it?
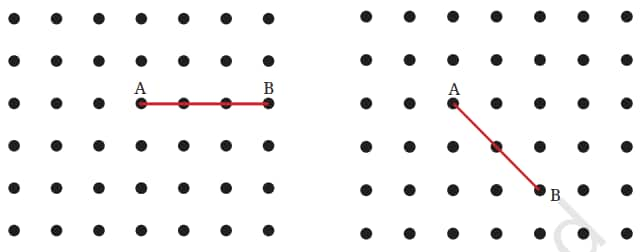
Answer: We can produce BA beyond A to join other points of the grid. Thus, we make a straight angle as shown in the figure below. Clearly, ∠CAB is a straight angle. There is only one way of doing it.
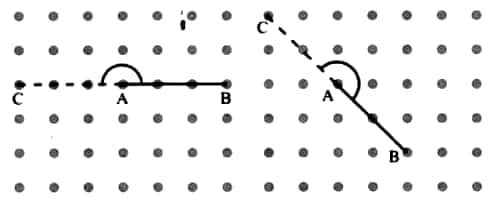
Question 3: Now join A to the other grid points in the figure by a straight line to get a right angle. What are all the different ways of doing it?
Hint: Extend the line further as shown in the figure below. To get a right angle at A, we need to draw a line through it that divides the straight angle CAB into two equal parts.
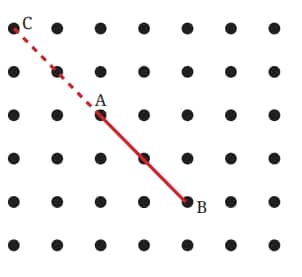
Answer: We can produce BA beyond A to make a straight angle, then through A, draw the line DE, which is perpendicular to BC, as shown in the figure below. Clearly, ∠DAB or ∠EAB is a right angle. There is only one way of doing it.
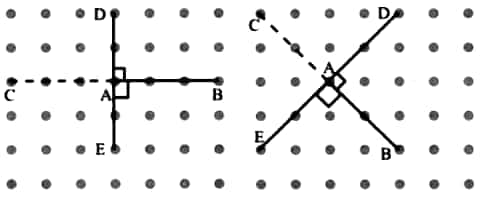
Question 4: Get a slanting crease on the paper. Now, try to get another crease that is perpendicular to the slanting crease.
a. How many right angles do you have now? Justify why the angles are exact right angles.
b. Describe how you folded the paper so that any other person who doesn’t know the process can simply follow your description to get the right angle.
Answer: We can fold the paper as shown in the figure.
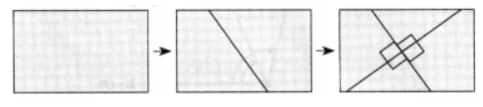
(a) We get 4 right angles. The angle formed at any point and one side of a line is always straight. The perpendicular drawn by the second crease through the vertex of a straight angle bisects it into two right angles.
(b) We first fold the paper to get a slanting crease and then fold the paper again in such a way that a part of the slanting crease falls on the other part of itself. Doing it carefully, we get another slanting line which is perpendicular to the first one. Thus, we get 4 right angles at the meeting point of the two lines, as shown in the figure.
|
Lines and Angles Class 6 Questions and Answers Page number: 31-32 Question: 4 |
Question 1: Identify acute, right, obtuse, and straight angles in the previous figures.
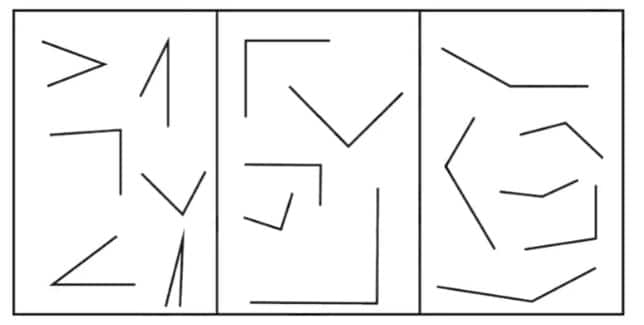
Answer:
|
Acute angle |
Right angle |
Obtuse angle |
|
|
|
|
Question 2: Make a few acute angles and a few obtuse angles. Draw them in different orientations.
Answer: Acute angles and obtuse angles in different orientations:
|
Acute angles |
Obtuse angles |
|
|
|
Question 3: Do you know what the words acute and obtuse mean? Acute means sharp, and obtuse means blunt. Why do you think these words have been chosen?
Answer: Yes, the words acute and obtuse in geometry have meanings that relate to their everyday usage:
Acute: The word acute means "sharp" in general English, which is why an acute angle is described this way. Acute angles are smaller than 90 degrees and visually appear "sharp" or narrow, like the tip of a knife or a point, which gives a sharp impression.
Obtuse: The word obtuse means "blunt" or "dull." An obtuse angle is greater than 90 degrees and appears wider or broader, which makes it look blunt or less sharp, much like a blunt object or a broad, dull edge.
Question 4: Find out the number of acute angles in each of the figures below
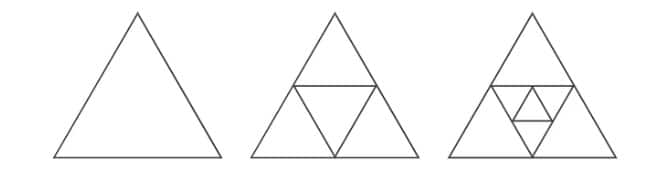
What will be the next figure, and how many acute angles will it have? Do you notice any pattern in the numbers?
Answer: We find the number of acute angles in the given figures is:
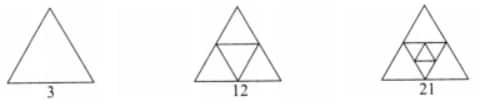
The next figure will be
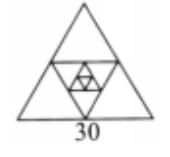
So, the number pattern is 3, 3 + 9 = 12, 12 + 9 = 21, 21 + 9 = 30,…
|
Lines and Angles Class 6 Questions and Answers Page number: 35 Question: 1 |
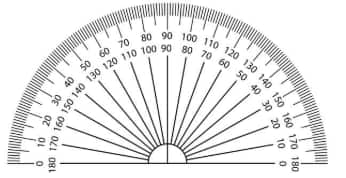
Question 1: Write the measures of the following angles: a. ∠ KAL Notice that the vertex of this angle coincides with the centre of the protractor. So the number of units of 1 degree angle between KA and AL gives the measure of ∠KAL. By counting, we get— ∠KAL = 30°. Making use of the medium-sized and large-sized marks, is it possible to count the number of units in 5s or 10s?
b. ∠WAL
c. ∠TAK
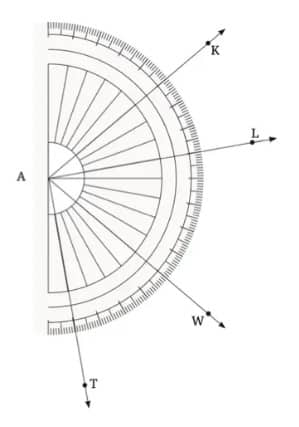
Answer:
(a) Yes, it is possible to count the number of units in 5s or 10s because there are also marking for each $5^{\circ}$ and $10^{\circ}$ on the protractor and the arms $\overrightarrow{\mathrm{AK}}$ and $\overrightarrow{\mathrm{AL}}$ pass through the $10^{\circ}$ markings.
(b) In the given figure, the arms $\overrightarrow{\mathrm{AL}}$ and $\overrightarrow{\mathrm{AW}}$ pass through the $10^{\circ}$ markings. There are five $10^{\circ}$ markings of scale where $\overrightarrow{\mathrm{AL}}$ and $\overrightarrow{\mathrm{AW}}$ pass. So, $\angle \mathrm{WAL}=50^{\circ}$.
(c) In the given figure, the arms $\overrightarrow{\mathrm{AK}}$ and $\overrightarrow{\mathrm{AT}}$ pass through the $10^{\circ}$ markings. There are twelve $10^{\circ}$ markings of scale where $\overrightarrow{\mathrm{AK}}$ and $\overrightarrow{\mathrm{AT}}$ pass. So, $\angle \mathrm{TAK}=120^{\circ}$.
|
Lines and Angles Class 6 Questions and Answers Page number: 40-43 Question: 9 |
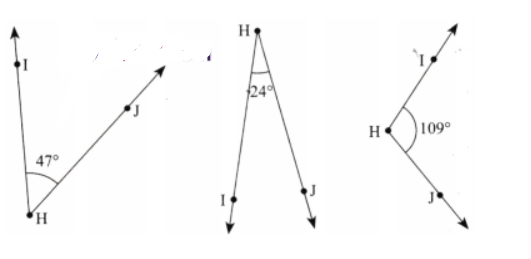
Question 1: Find the degree measures of the following angles using your protractor.
Answer:
Question 2: Find the degree measures of different angles in your classroom using your protractor.
Answer: Take different angles and measure them.
Question 3: Find the degree measures for the angles given below. Check if your paper protractor can be used here!
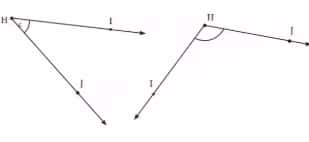
Answer:
The degree measures for the angles using a paper protractor are given below:
Question 4: How can you find the degree measure of the angle given below using a protractor?
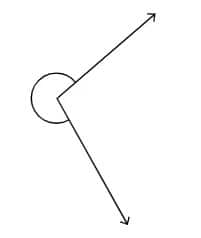
Answer: We can draw a ray opposite to one of the arms and split the angle into two parts - a straight angle and an acute angle. Measure the acute angle (∠1 = 80°) using a protractor and add it to 180°. It would be the measure of the required angle (180° + 80° = 260°).
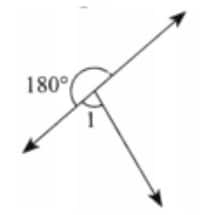
Question 5: Measure and write the degree measures for each of the following angles:
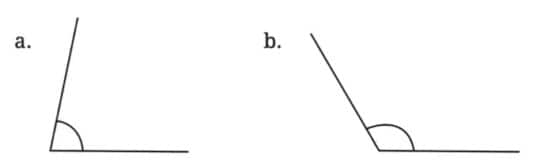

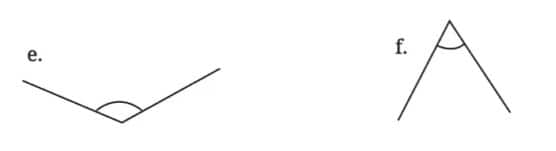
Answer:
(a) 80°
(b) 120°
(c) 60°
(d) 130°
(e) 125°
(f) 62°
Question 6: Find the degree measures of ∠BXE, ∠CXE, ∠AXB, and ∠BXC.
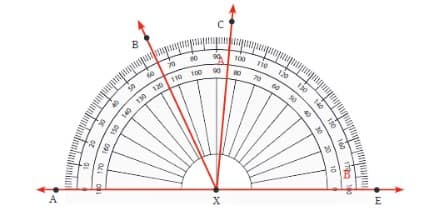
Answer: The degree measures of ∠BXE, ∠CXE, ∠AXB, and ∠BXC are as follows:
∠BXE = 115°
∠CXE = 85°
∠AXB = 65°
∠BXC = 30°
Question 7: Find the degree measures of ∠PQR, ∠PQS, and ∠PQT
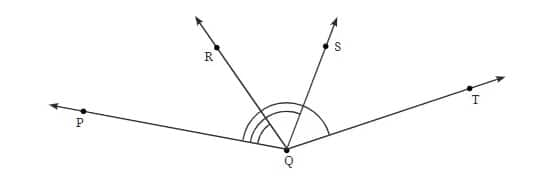
Answer: The degree measures of ∠PQR, ∠PQS, and ∠PQT are as follows:
∠PQR=45°
∠PQS=100°
∠PQT=152°
Question 8: Make the paper craft as per the given instructions. Then, unfold and open the paper fully. Draw lines on the creases made and measure the angles formed.
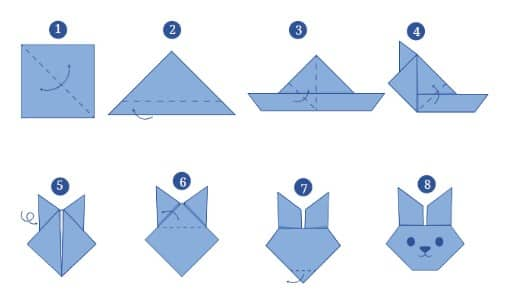
Answer:
Step 1: Fold the square diagonally to form a triangle.
Step 2: Fold the bottom tip of the triangle upwards.
Step 3: Fold the right and left corners upwards to make ears.
Step 4: Fold the side edges inward to form the sides of the face.
Step 5: Fold the ear tips outward slightly.
Step 6: Fold the top corner behind the model to round the head.
Step 7: Fold the bottom point backwards.
Step 8: Draw eyes, nose, and whiskers to complete the bunny!
In the complete bunny face, we will have multiple angles:
The ears form acute angles (around 30° to 45°). Carefully unfold the entire model to return to a flat sheet.
The face near the chin forms an obtuse angle, close to 120°.
The sides of the face are around 90° to 120°, depending on the precision of the folds.
Question 9: Measure all three angles of the triangle shown in Fig. 2.21 (a), and write the measures down near the respective angles. Now add up the three measures. What do you get? Do the same for the triangles in Fig. 2.21 (b) and (c). Try it for other triangles as well, and then make a conjecture for what happens in general! We will come back to why this happens in a later year.
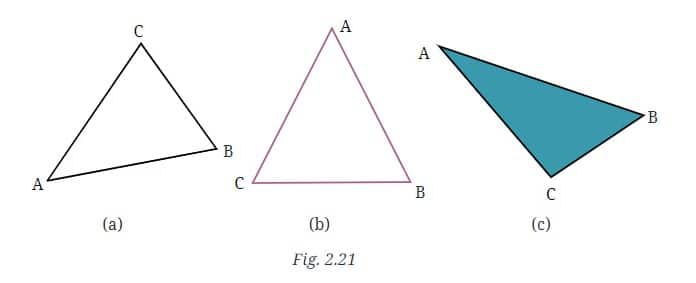
Answer:
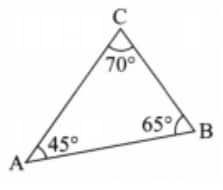
a) The sum of the three angles of the triangle: 45° + 65° + 70° = 180°
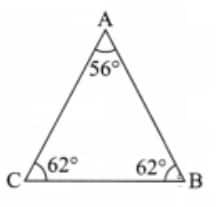
b) The sum of the three angles of the triangle: 56° + 62° + 62° = 180°
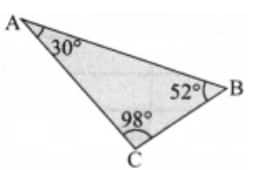
c) The sum of the three angles of the triangle: 30° + 52° + 98° = 180°
|
Lines and Angles Class 6 Questions and Answers Page number: 45-46 Question: 5 |
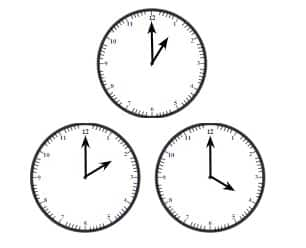
Question 1: Angles in a clock:
a. The hands of a clock make different angles at different times. At 1 o’clock, the angle between the hands is 30°. Why?
b. What will be the angle at 2 o’clock? And at 4 o’clock? 6 o’clock?
c. Explore other angles made by the hands of a clock.
Answer:
a) The clock dial has been divided into 12 equal parts. And the dial of the clock represents an angle of 360°.
So, the angle measure of each part is $\frac{360°}{12}$ = 30°.
Thus, at 1 o'clock, the angle between the hands is 30°.
b) From 12 to 2, we have 2 parts at 2 o'clock. So, the angle between the hands is 60°.
Similarly, between 12 and 4, we have four parts.
So, at 4 o'clock, the angle between the hands is 120°. Similarly, at 6 o'clock, the angle between the hands is 180°.
c) The other angles made by the hands of a clock:
Angle between hands at 5o′ clock = 5 × 30° = 150°
Angle between hands at 7 o' clock = 7 × 30° = 210°
Angle between hands at 8o′ clock = 8 × 30° = 240°
Question 2: The angle of a door: Is it possible to express the amount by which a door is opened using an angle? What will be the vertex of the angle, and what will be the arms of the angle?

Answer: Yes, it is possible to express the amount by which a door is opened using an angle. The vertex of the angle will be the hinge of the door, and the arms of the angle will be the wall and the door itself.
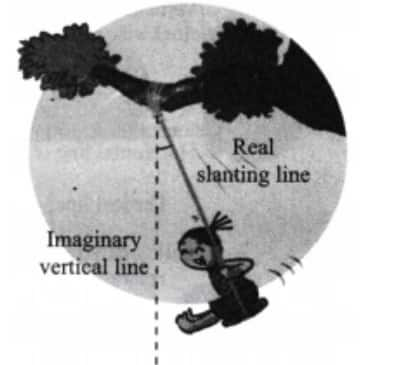
Question 3: Vidya is enjoying her time on the swing. She notices that the greater the angle with which she starts the swinging, the greater is the speed she achieves on her swing. But where is the angle? Are you able to see any angle?

Answer: Vidya's original position is along the vertical line. When she starts swinging, the rope of the swing is along the slanting line, which makes an angle with the imaginary vertical line. The speed depends on this angle.
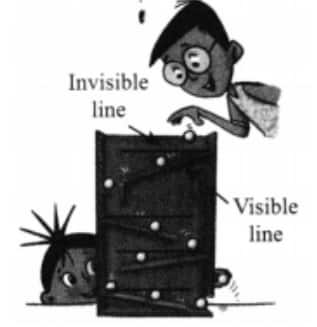
Question 4: Here is a toy with slanting slabs attached to its sides; the greater the angles or slopes of the slabs, the faster the balls roll. Can angles be used to describe the slopes of the slabs? What are the arms of each angle? Which arm is visible and which is not?

Answer: Yes, angles can be used to describe the slopes of the slabs. Horizontal imaginary line and slab are the arms of each angle. Here, the slab arm is visible, but the horizontal line is not visible.
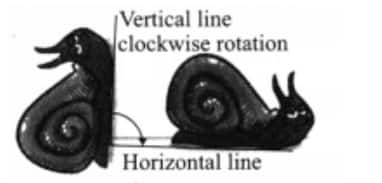
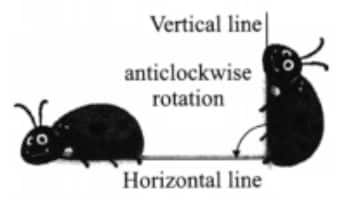
Question 5: Observe the images below, where there is an insect and its rotated version. Can angles be used to describe the amount of rotation? How? What will be the arms of the angle and the vertex? Hint: Observe the horizontal line touching the insects.

Answer: Observe the vertical and horizontal lines touching the insects. The rotation from vertical to horizontal position makes an angle. We can imagine the meeting point of the two lines as the vertex, and these two lines as arms of the angle, as shown in the picture.
|
Lines and Angles Class 6 Questions and Answers Page number: 49-50 Question: 3 |
Question 1: In Fig. 2.23, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.
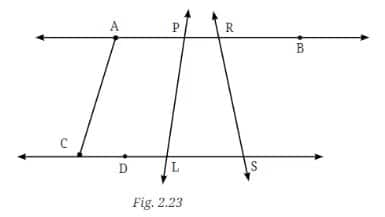
Answer:
The table to record my guesses and actual measurements:
|
Angle |
Guessed measure |
Actual measure |
|
∠PAC |
120° |
115° |
|
∠APD |
45° |
50° |
|
∠DPS |
60° |
60° |
|
∠LPR |
110° |
110° |
|
∠PLS |
90° |
80° |
|
∠ARP |
360° |
360° |
|
∠PRS |
110° |
115° |
|
∠RSL |
80° |
75° |
|
∠ALC |
45° |
50° |
Question 2: Use a protractor to draw angles having the following degree measures: a. 110° b. 40° c. 75° d. 112° e. 134°
Answer:
a) 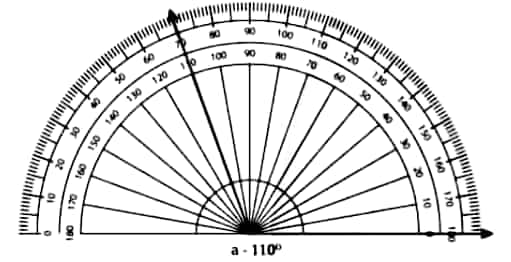
b) 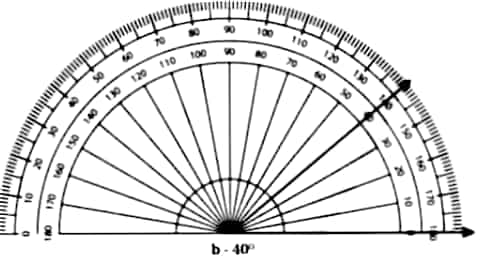
c) 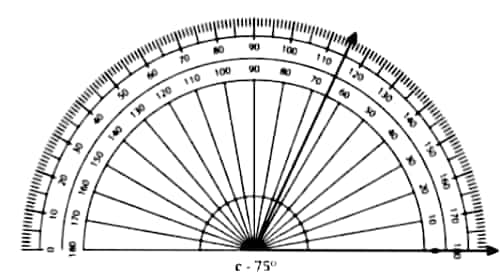
d) 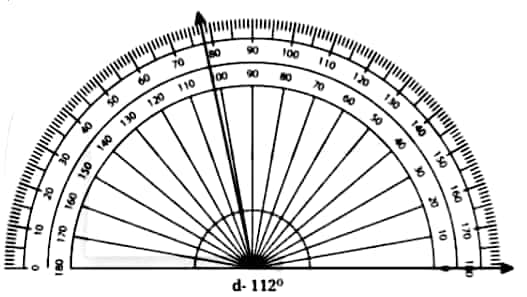
e) 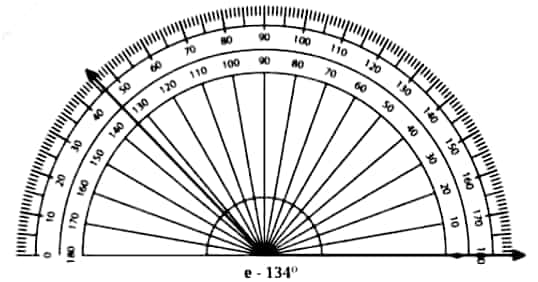
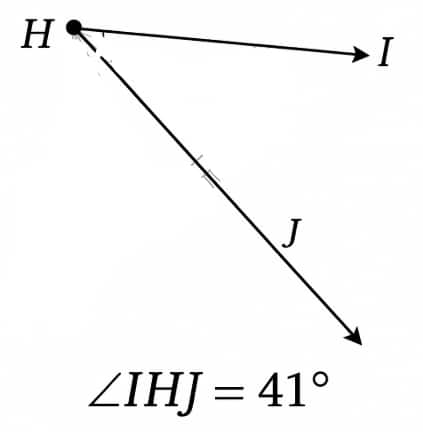
Question 3: Draw an angle whose degree measure is the same as the angle given below:
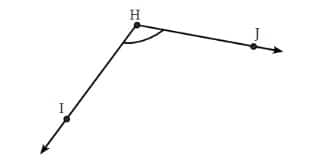
Also, write down the steps you followed to draw the angle.
Answer: We can draw an angle equal to the given angle by following these steps:
Step I: Draw a ray $\overrightarrow{AB}$.

Step II: Measure the angle IHJ. It is 118°.
Step III: Place the centre of the protractor at A and the zero edge along $\overrightarrow{AB}$.
Step IV: Start counting from zero near B. Mark a point C at 118°.
Step V: Join AC.
Thus, ∠BAC = ∠IHJ.
|
Lines and Angles Class 6 Questions and Answers Page number: 51-52 Question: 2 |
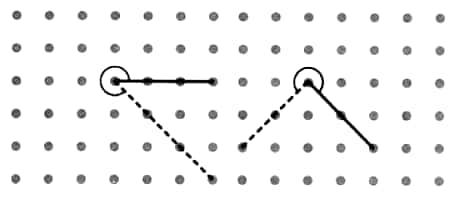
Question 1: In each of the grids below, join A to other grid points in the figure by a straight line to get:
a. An acute angle
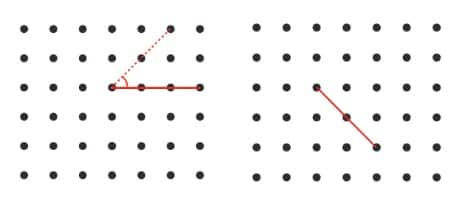
b. An obtuse angle
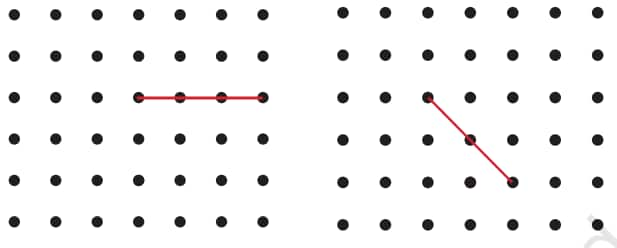
c. A reflex angle
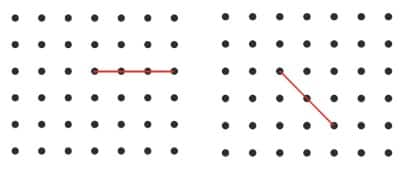
Mark the intended angles with curves to specify the angles. One has been done for you.
Answer:
a) Acute angle
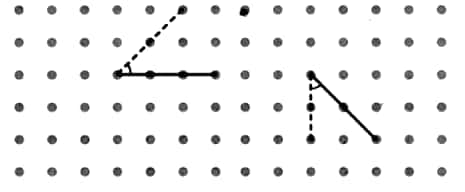
b) Obtuse angle
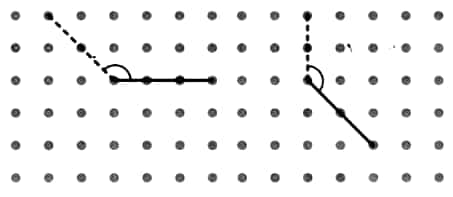
c) Reflex angle
Question 2: Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex.
a. ∠PTR
b. ∠PTQ
c. ∠PTW
d. ∠WTP
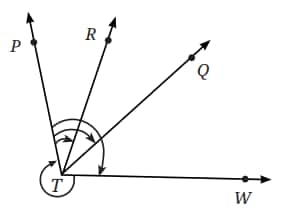
Answer:
Using a protractor, we find the measure of each angle and then classify each angle as follows:
(a) ∠PTR = 31°, acute angle
(b) ∠PTQ = 60°, acute angle
(c) ∠PTW = 104°, obtuse angle
(d) ∠WTP = 360° − 104° = 256°, reflex angle.
|
Lines and Angles Class 6 Questions and Answers Page number: 53-54 Question: 7 |
Question 1: Draw angles with the following degree measures: a. 140° b. 82° c. 195° d. 70° e. 35°
Answer:
a) 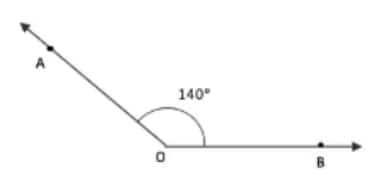
b) 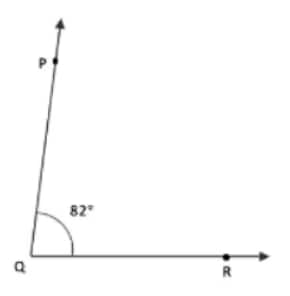
c) 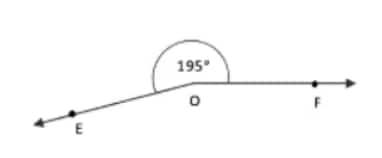
d) 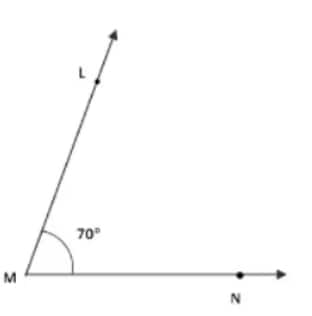
e) 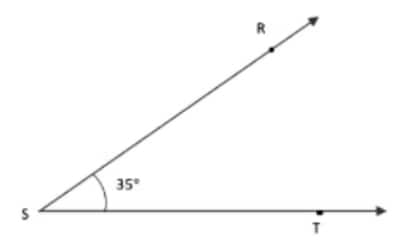
Question 2: Estimate the size of each angle and then measure it with a protractor:
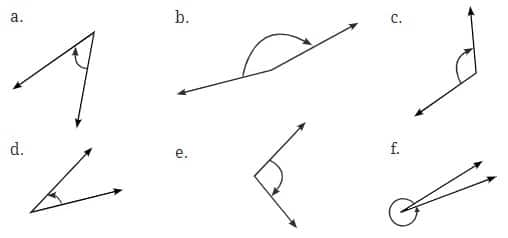
Classify these angles as acute, right, obtuse, or reflex angles.
Answer:
(a) 45°, acute angle
(b) 169°, obtuse angle
(c) 120°, obtuse angle
(d) 33°, acute angle
(e) 99°, obtuse angle
(f) 348°, reflex angle
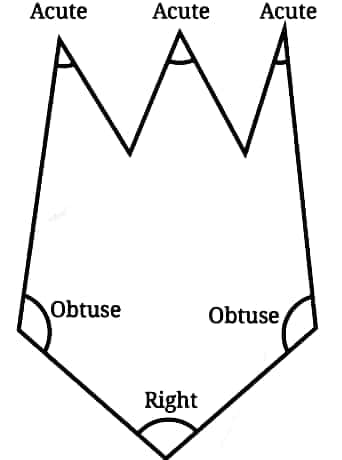
Question 3: Make any figure with three acute angles, one right angle, and two obtuse angles.
Answer: Figure with three acute angles, one right angle and two obtuse angles:
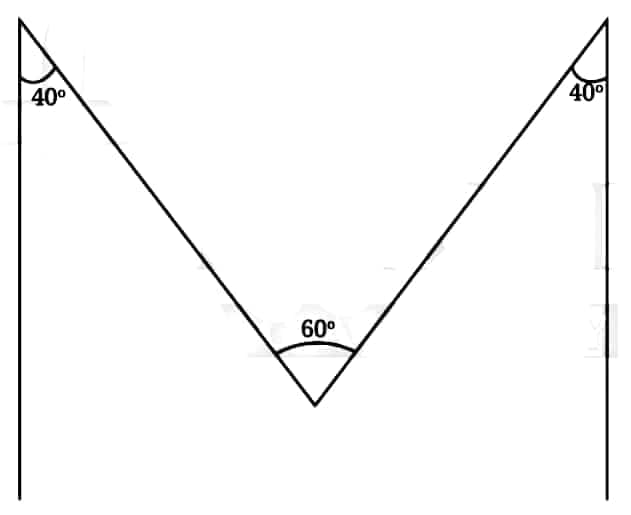
Question 4: Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.
Answer: The letter 'M' such that the angles on the sides are 40° each and the angle in the middle is 60°.
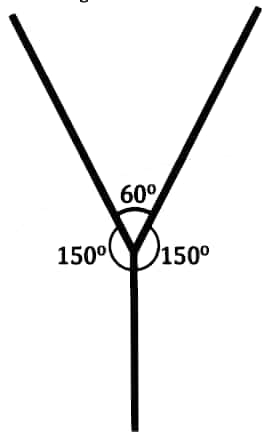
Question 5: Draw the letter ‘Y’ such that the three angles formed are 150°, 60°, and 150°.
Answer: The letter 'Y′ such that the three angles formed are 150°, 60°, and 150°.
Question 6: The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes?

Answer: The Ashoka Chakra resembles a circle. So its degree measure is 360°.
Dividing it into 24 equal parts by spokes, the measure of each part = $\frac{360°}{24}$ = 15°
Thus, the degree measure of the angle between two spokes next to each other is 15°.
The largest acute angle formed between two spokes is 5 × 15° = 75°.
Question 7: Puzzle: I am an acute angle. If you double my measure, you get an acute angle. If you triple my measure, you will get an acute angle again. If you quadruple (four times) my measure, you will get an acute angle yet again! But if you multiply my measure by 5, you will get an obtuse angle measure. What are the possibilities for my measure?
Answer: As per the given condition, we have $4 \times$ acute angle $<90^{\circ}$ and $5 \times$ acute angle $>90^{\circ}$
$\Rightarrow$ acute angle $<\frac{90^{\circ}}{4}=22 \frac{1}{2}^{\circ}$ and acute angle $>\frac{90^{\circ}}{5}=18^{\circ}$
So, possible measures of the acute angle would be $19^{\circ}, 20^{\circ}, 21^{\circ}$ and $22^{\circ}$ in whole numbers.
NCERT Class 6 Maths Chapter 2 Solutions: Topics
Students will explore the following topics in NCERT Class 6 Maths Chapter 2 Lines and Angles:
- 2.1 Point
- 2.2 Line Segment
- 2.3 Line
- 2.4 Ray
- 2.5 Angle
- 2.6 Comparing Angles
- 2.7 Making Rotating Arms
- 2.8 Special Types of Angles
- 2.9 Measuring Angles
- 2.10 Drawing Angles
- 2.11 Types of Angles and Their Measures
Class 6 Maths Chapter 2 Lines and Angles solutions: Extra Question
Question:
The spokes of a bicycle wheel form a pattern. There are 18 spokes evenly spaced on the wheel. What is the degree measure of the angle between two spokes next to each other?
Solution:
Since the spokes are evenly spaced on the wheel, the total angle around the centre of the wheel is $360^{\circ}$.
To find the angle between two adjacent spokes, divide $360^{\circ}$ by the number of spokes:
$\text { Angle between adjacent spokes }=\frac{360^{\circ}}{18}=20^{\circ}$
So, the angle between two adjacent spokes is 20°.
Class 6 Maths Chapter 2 Lines and Angles solutions: Important Notes
All the important concepts, formulas, and definitions of the NCERT class 6 maths chapter 2, Lines and Angles, are given below as notes. These notes will help you understand this chapter better and solve the Lines and Angles NCERT solutions with ease.
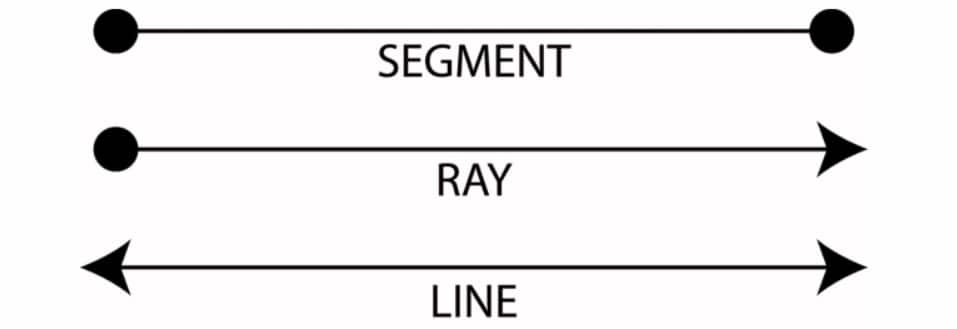
Point: If we mark a dot somewhere on our notebook, we can call it a point in geometry. It is represented by capital letters like P, Q and doesn't have any fixed length, breadth, or height.
Line Segment: If we mark any two points and join them with a line that has a fixed length, then it is a line segment. It is represented by capital letters like AB
Line: A line is extended in both directions till infinity and does not have a fixed length. It is represented by showing arrows on both sides of a line.
Ray: A ray is defined as having a fixed point, and the other side extends to infinity. Some of the examples include light coming from a lighthouse or the sun's rays.
Angle: An angle is formed when two rays have a common starting point and the other two ends extend to infinity. The common point is called the vertex, and the rays are called the arms of the angle.
We can find angles in our daily life, for example, the hands of a clock. The exact measurement of an angle can be calculated with the help of a protractor.
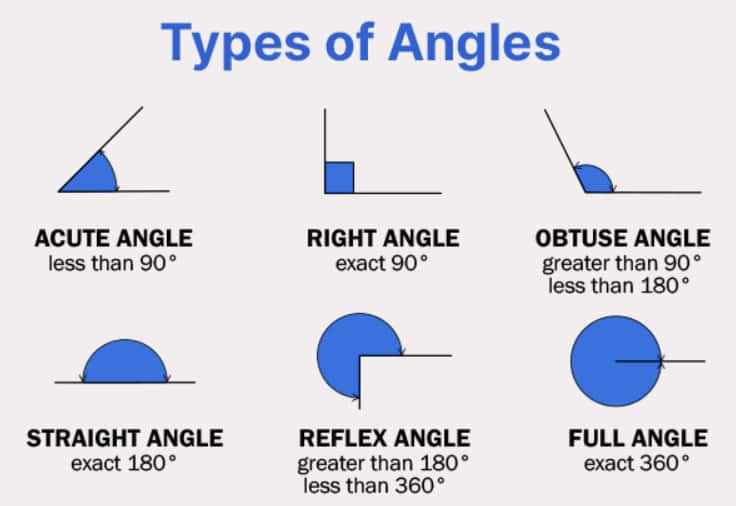
Right angle: It is an angle that measures exactly 90 degrees. For example, the angle made by the Clock when it turns 3 pm.
Acute angle: It is an angle that measures less than 90 degrees.
Obtuse angle: It is an angle that measures more than 90 degrees but less than 180 degrees.
Reflex angle: It is an angle that measures more than 180 degrees but less than 360 degrees.
Lines and Angles Class 6 NCERT Solutions: Points to Remember
Given below are some important points about the Class 6 Maths NCERT Chapter 2, Lines and Angles:
Point: A dot representing a location or a position with no length or breadth is a point.
Line: A straight path extending in both directions infinitely.
Line Segment: A line with a definite length is called a line segment.
Ray: A line starting at a fixed point and extending infinitely in the other direction is called a ray.
Angle: An angle consists of two rays with a common starting point.
Types of angles: Angles are of 4 types, namely, acute angle, right angle, obtuse angle and reflex angle.
NCERT Solutions for Class 6 Maths Chapter Wise
For students' preparation, Careers360 has gathered all Class 6 Maths NCERT solutions here for quick and convenient access.
NCERT Books and the NCERT Syllabus
Students can also check the NCERT Books and the NCERT Syllabus for Class 6 here:
Frequently Asked Questions (FAQs)
An angle is formed when two rays have a common starting point and the other two ends extend to infinity. The common point is called the vertex, and the rays are called the arms of the angle.
The following topics are covered in the NCERT syllabus of Class 6 Maths chapter 2:
- Point
- Line segment
- Line
- Ray
- Angle
- Types of Angles
If we mark any two points and join them with a line that has a fixed length, then it is a line segment.
Yes, many educational platforms, such as Careers360, offer free downloadable PDFs of NCERT Class 6 Maths Chapter 2 Lines and Angles solutions. Students can find the free downloadable PDF in this article itself.
NCERT Solutions help students understand concepts clearly by providing step-by-step answers to textbook questions. They are great for exam preparation and completing homework accurately and efficiently.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters