NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

Edited By Ramraj Saini | Updated on Nov 30, 2023 10:46 AM IST

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry are discussed in this article. These NCERT solutions are created by the expert team at careers360 considering the latest CBSE syllabus 2023. Constructions of figures or sketches are mandatory for the design of different types of equipment, instruments, buildings, etc. In CBSE NCERT solutions for Class 6 Maths chapter 14 practical geometry, you will get questions related to constructions of figures using rulers and compass.

Latest: Important Maths Formulas for Class 6 - Chapterwise

This Story also Contains

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry - Important Points
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry (Intext Questions and Exercise)
NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.1
NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.2
NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.3
NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.4
NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.5
NCERT Class 6 Maths Chapter 14 Practical Geometry Topic 14.5.4 Angles of Special Measures
NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise: 14.6
Question: 1 Draw POQ of measure 75° and find its line of symmetry.
Main Topics of NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry
NCERT Solutions for Class 6 Mathematics Chapter Wise
Key Features of NCERT Solutions for Class 6 Maths Chapter 14
NCERT Solutions for Class 6 Subject Wise

$NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry$

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

As per the NCERT syllabus for Class 6 Maths, the important topics of this chapter are the construction of the circle of a given radius using a compass, the construction of line segments and angles, etc. In the last exercise of this chapter as mentioned in the NCERT Books for Class 6 Maths, you will get questions related to measuring of angle using a compass and ruler. In some questions in NCERT, you will be drawing lines using the compass. There are many other constructions explained in 6 exercises of NCERT solutions for practical geometry class 6. You will get NCERT Solutions from Class 6 to 12 for Science and Math by clicking on the above link.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry - Important Points

Geometrical shapes: This class 6th maths chapter 14 focuses on the methods used to draw various geometrical shapes. The shapes are constructed using mathematical instruments such as a graduated ruler, compasses, divider, set-squares, and a protractor.

Constructions using ruler and compasses:

(i) Circle: A circle can be drawn when the length of its radius is known. The compasses are used to measure and draw the circle.

(ii) Line segment: With the ruler and compasses, a line segment can be constructed when its length is given.

(iii) Copy of a line segment: The compasses are used to create an exact copy of a given line segment.

For more, Download Ebook - NCERT Class 6 Maths: Chapterwise Important Formulas And Points

(iv) Perpendicular to a line through a point:

(a) On the line: A perpendicular line can be drawn through a point that lies on the given line.
(b) Not on the line: A perpendicular line can be drawn through a point that does not lie on the given line.

(v) Perpendicular bisector: The perpendicular bisector of a line segment, which divides it into two equal halves, can be constructed.

(vi) Angle of a given measure: An angle with a specific measure can be constructed using the ruler and compasses.

(vii) Copy of an angle: With the ruler and compasses, an exact copy of a given angle can be drawn.

(viii) Bisector of an angle: The bisector of a given angle, which divides it into two equal angles, can be constructed.

(ix) Special angles: The class 6 maths chapter 14 chapter also covers the construction of angles with special measures such as 90 degrees, 45 degrees, 60 degrees, 30 degrees, 120 degrees, and 135 degrees. These angles are constructed using the ruler and compasses

Free Download NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry For CBSE Exam

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

Download PDF

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry (Intext Questions and Exercise)

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.1

Question: 1 Draw a circle of radius 3.2 cm.

Answer: To draw a circle of radius 3.2 cm follow the steps given below:

(i) Take compasses for the required radius of 3.2 cm.

(ii) Mark point O where you want the centre of the circle.

(iii) After placing the compass on O, rotate the compasses slowly to make the circle. 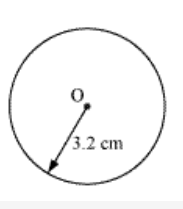1643782376732

Question: 2 With the same centre O, draw two circles of radii 4 cm and 2.5 cm .

Answer: To draw the required circle follow the steps as follows:

(i) First, Set the compass for radius 4 cm

(ii) Mark point O which will be the centre for the circles.

(iiI) Place the pointer of compasses on O.

(iv) Turn the compasses slowly to draw the circle.

Repeat above 4 steps with the compass set at 2.5 cm 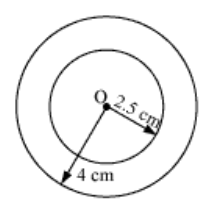1643782419227

Question:3 Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?

Answer: By joining the ends of the two diameters, we get a rectangle.

Therefore, by measuring, we find that $AB=CD$ and $BC=AD$ , i.e, pairs of opposite sides are equal and also $\angle A = \angle B = \angle C = \angle D = 90^{\circ}$ .

and each angle is fo $90^{\circ}.$

Hence, it is a rectangle: 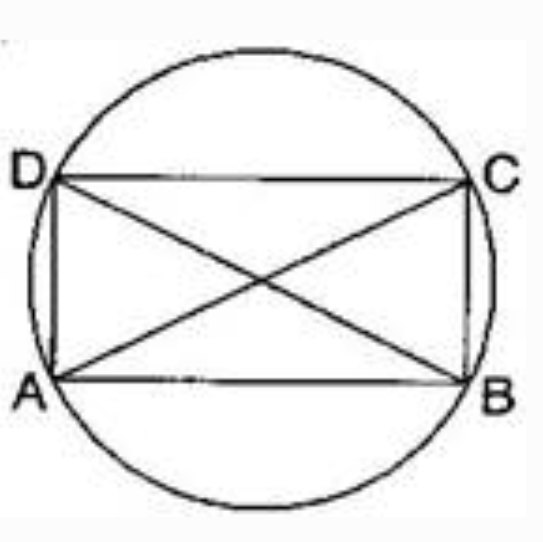1643782458502

If the diameters are perpendicular to each other, then by joining the ends of two diameters, we get a square.

Then, by measuring the length of the side we find that $AB=BC=CD=DA$ . that is all sides are of the same length also, $\angle A = \angle B = \angle C = \angle D = 90^{\circ}$ , that is each angle is $90^{\circ}.$

Hence, it is a square: 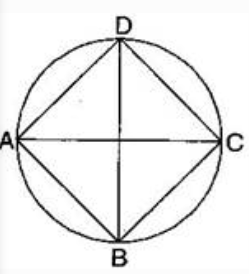1643782484441

Question: 4 Draw any circle and mark points A, B, and C such that

(a) A is on the circle. (b) B is in the interior of the circle.
(c) C is in the exterior of the circle.

Answer: To draw the circle with the given conditions:

First, mark point 'O' as the centre and place the pointer of the compasses at 'O' then turn the compasses slowly to complete the circle.

Now, mark point A on the circle, mark the point 'B' in the interior of the circle, also point 'C' exterior to the circle. 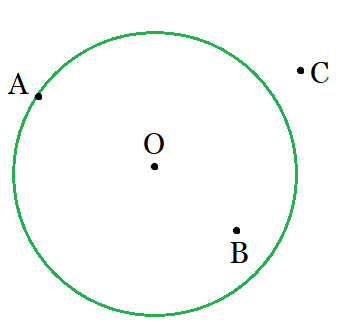1643782537160

Question: 5 Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether $\overline{AB}$ and $\overline{CD}$ are at right angles.

Answer: First, draw two circles of equal radii taking A and B as their centre and they intersect at C and D. Then, join AB and CD.

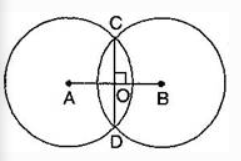1643782571220 From the figure, AB and CD intersect at right angle with

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.2

Question: 1 Draw a line segment of length 7.3 cm using a ruler.

Answer: Let the line segment be 'AB':

Then, follows these steps:

(i) Place the zero mark of the ruler at a point A.

(ii) Mark point B at a distance of 7.3cm from A.

(iii) Now, join AB.

Then, AB is the required line segment of the length of 7.3 cm.

Question: 2 Construct a line segment of length 5.6 cm using ruler and compasses.

Answer:

1643782642506 (i) Draw a line ′l′. Mark a point A on this line.

(ii) Place the compasses pointer on the zero mark of the ruler. Open it to place the pencil point up to 5.6 cm mark.

(iii) Without changing the opening of the compasses. Place the pointer on A and cut an arc at B on line l.

$\bar{AB}$ is the required line segment of length 5.6 cm.

Question: 3 Construct AB of length 7.8 cm. From this, cut off $\overline{AB}$ of length 4.7 cm. Measure $\overline{BC}$ .

Answer: The steps of constructions:

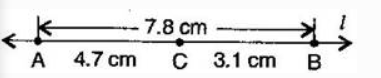1643782667509 (i) Place the zero mark of the ruler at A.

(ii) Mark a point B at a distance 7.8 cm from A.

(iii) Again, mark a point C at a distance 4.7 from A.

By measuring $\bar{BC}$ , we find that BC = 3.1 cm

Question: 4 Given $\overline{AB}$ of length 3.9 cm, construct $\overline{PQ}$ such that the length of $\overline{PQ}$ is twice that of $\overline{AB}$ . Verify by measurement.

1657530982905

( Hint : Construct $\overline{PX}$ such that length of $\overline{PX}$ = length of $\overline{AB}$ ; then cut off $\overline{XQ}$ such that $\overline{XQ}$ also has the length of $\overline{AB}$ .)

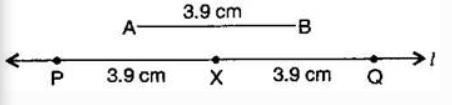
Answer: The steps of constructions are following:

(i) Draw a line ′l′.

(ii) Construct $\bar{PX}$ such that length of $\bar{PX}$ = length of $\bar{AB}$

(iii) Then cut of $\bar{XQ}$ such that $\bar{XQ}$ also has the length of $\bar{AB}$ .

(iv) Thus the length of $\bar{PX}$ and the length of $\bar{XQ}$ added together make twice the length of $\bar{AB}$ .

Verification :

By measurement we find that PQ = 7.8 cm

= 3.9 cm + 3.9 cm = $\bar{AB} + \bar{AB}$ = $2\times\bar{AB} .$

Question: 5 Given $\overline{AB}$ of length 7.3 cm and $\overline{CD}$ of length 3.4 cm, construct a line segment $\overline{XY}$ such that the length of $\overline{XY}$ is equal to the difference between the lengths of $\overline{AB}$ and $\overline{CD}$ . Verify by measurement .

Answer: The steps of construction are as follows:

(i) Draw a line ′l′ and take a point X on it.

(ii) Construct $\bar{XZ}$ such that length $\bar{XZ}$ = length of $\bar{AB}$ = 7.3 cm

(iii) Then cut off $\bar{ZY}$ = length of $\bar{CD}$ = 3.4 cm

(iv) Thus the length of $\bar{XY}$ = length of $\bar{AB}$ – length of $\bar{CD}$

1643782715163

Verification :

By measurement we find that length of $\bar{XY}$ = 3.9 cm

$= 7.3 cm - 3.4cm = \bar{AB} - \bar{CD}$

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.3

Question: 1 Draw any line segment $\overline{PQ}$ . Without measuring $\overline{PQ}$ , construct a copy of $\overline{PQ}$ .

Answer: The steps of constructions are the following: 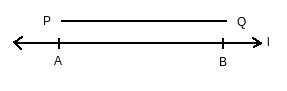1643782797660

(i) Given $\bar{PQ}$ whose length is not known.

(ii) Fix the compasses pointer on P and the pencil end on Q. The opening of the instrument now gives the length of $\bar{PQ}$ .

(iii) Draw any line $'l'$ . Choose a point A on $'l'$ . Without changing the compasses setting, place the pointer on A.

Draw an arc that cuts at $'l'$ a point, say B. Now $\bar{AB}$ is a copy of $\bar{PQ}$ .

Question:2 Given some line segment $\overline{AB}$ , whose length you do not know, construct $\overline{PQ}$ such that the length of $\overline{PQ}$ is twice that of $\overline{AB}$ .

Answer: The steps of construction are followings: 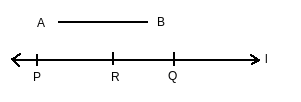1643782823669

(i) Given $\bar{AB}$ whose length is not known.

(ii) Fix the compasses pointer on A and the pencil end on B. The opening of the instrument now gives the length of $\bar{AB}$ .

(iii) Draw any line $'l'$ . Choose a point P on $'l'$ . Without changing the compasses setting, place the pointer on Q.

(iv) Draw an arc that cuts $'l'$ at a point R.

(v) Now place the pointer on R and without changing the compasses setting, draw another arc that cuts $'l'$ at a point Q.

Thus $\bar{PQ}$ is the required line segment whose length is twice that of AB.

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.4

Question: 1 Draw any line segment $\overline{AB}$ . Mark any point M on it. Through M, draw a perpendicular to $\overline{AB}$ . (use ruler and compasses)

Answer: The steps of constructions are the following: 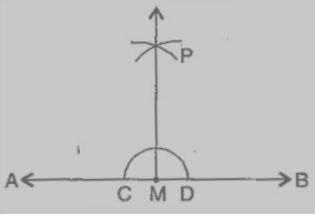1643782859391

(i) With M as the centre and a convenient radius, draw an arc intersecting the line AB at two points C and B.

(ii) With C and D as centres and a radius greater than MC, draw two arcs, which cut each other at P.

(iii) Join PM. Then PM is perpendicular to AB through point M.

Question: 2 Draw any line segment $\overline{PQ}$ . Take any point R not on it. Through R, draw a perpendicular to $\overline{PQ}$ . (use ruler and set-square)

Answer: The steps of constructions are:

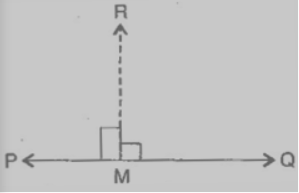
1643782899040

(i) Place a set-square on $PQ$ such that one arm of its right angle aligns along $PQ$ .

(ii) Place a ruler along the edge opposite to the right angle of the set-square.

(iii) Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.

(iv) Join RM along the edge through R meeting $PQ$ at M. Then RM ⊥ PQ.

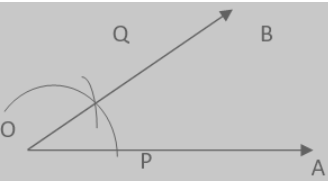
Question: 3 Draw a line l and a point X on it. Through X, draw a line segment $\overline{XY}$ perpendicular to l . Now draw a perpendicular to $\overline{XY}$ at Y. (use ruler and compasses)

Answer: The steps of construction are as follows:

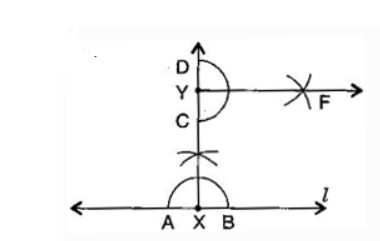
1643782927968

(i) Draw a line $'l'$ and take point X on it.

(ii) With X as the centre and a convenient radius, draw an arc intersecting the line $'l'$ at two points A and B.

(iii) With A and B as centres and a radius greater than XA, draw two arcs, which cut each other at C.

(iv) Join AC and produce it to Y. Then XY is perpendicular to $'l'$ .

(v) With Y as the centre and a convenient radius, draw an arc intersecting XY at two points C and D.

(vi) With C and D as centres and radius greater than YD, draw two arcs which cut each other at F.

(vii) Join YF, then YF is perpendicular to XY at Y.

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.5

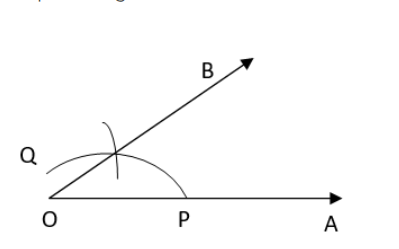
Question: 1 Draw $\overline{AB}$ of length 7.3 cm and find its axis of symmetry.

Answer: The axis of symmetry of the line segment $\bar{AB }$ will be the perpendicular bisector of $\bar{AB }$ . So, draw the perpendicular bisector of AB.

The steps of constructions are as follows: 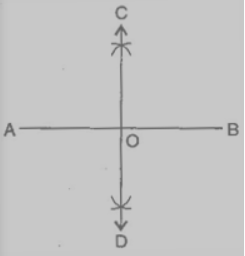1643782960670

(i) Draw a line segment $\bar{AB }$ = 7.3 cm

(ii) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.

(iii) Join CD. Then CD is the axis of symmetry of the line segment AB.

Question: 2 Draw a line segment of length 9.5 cm and construct its perpendicular bisector.

Answer: The steps of constructions are: 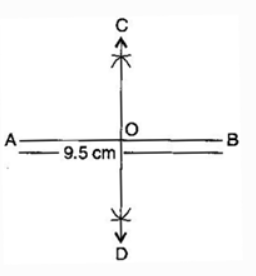1643782985978

(i) Draw a line segment $\bar{AB}$ = 9.5 cm

(ii) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C and D.

(iii) Join CD. Then CD is the perpendicular bisector of $\bar{AB}$ .

Question:3 Draw the perpendicular bisector of XY whose length is 10.3 cm. (a) Take any point P on the bisector drawn. Examine whether PX = PY. (b) If M is the midpoint of XY, what can you say about the lengths MX and XY?

Answer: Follow the steps to draw the perpendicular bisector of a line XY.

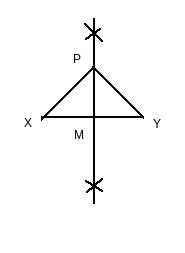
1643783022315

a) PX= PY

b)MX=MY

Question: 4 Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.

Answer: The steps of constructions are:

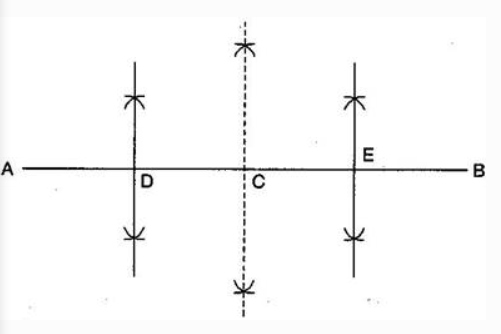
1643783061230

(i) Draw a line segment AB = 12.8 cm

(ii) Draw the perpendicular bisector of $\bar{AB}$ which cuts it at C. Thus, C is the mid-point of $\bar{AB}$ .

(iii) Draw the perpendicular bisector of $\bar{AC}$ which cuts it at D. Thus D is the mid-point of .

(iv) Again, draw the perpendicular bisector of $\bar{CB}$ which cuts it at E. Thus, E is the mid-point of $\bar{CB}$ .

(v) Now, point C, D, and E divide the line segment $\bar{AB}$ in the four equal parts.

(vi) By actual measurement, we find that

$\bar{AD} = \bar{DC} = \bar{CE} = \bar{EB} = 3.2cm$

Question: 5 With PQ of length 6.1 cm as diameter, draw a circle.

Answer: The steps of constructions are: 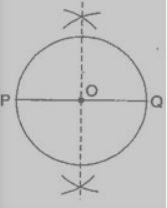1643783103487

(i) Draw a line segment $\bar{PQ}$ = 6.1 cm.

(ii) Draw the perpendicular bisector of PQ which cuts, it at O. Thus O is the mid-point of $\bar{PQ}$ .

Taking O as the centre and OP or OQ as radius draw a circle where the diameter is the line segment $\bar{PQ}$ .

Question: 6 Draw a circle with centre C and radius 3.4 cm. Draw any chord $\overline{AB}$ . Construct the perpendicular bisector of $\overline{AB}$ and examine if it passes through C.

Answer: The steps of constructions are: 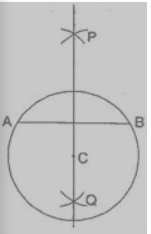1643783143570

(i) Draw a circle with centre C and radius 3.4 cm.

(ii) Draw any chord $\bar{AB}$ .

(iii) Taking A and B as centres and radius more than half of $\bar{AB}$ , draw two arcs which cut each other at P and Q.

(iv) Join PQ. Then PQ is the perpendicular bisector of $\bar{AB}$ .

This perpendicular bisector of $\bar{AB}$ passes through the centre C of the circle.

Question: 7 Repeat Question 6, if AB happens to be a diameter.

Answer: The steps of constructions are:

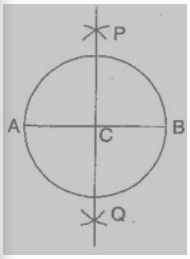
1643783196739

(i) Draw a circle with centre C and radius 3.4 cm.

(ii) Draw its diameter $\bar{AB}$

(iii) Taking A and B as centres and radius more than half of it, draw two arcs which intersect each other at P and Q.

(iv) Join PQ. Then PQ is the perpendicular bisector of $\bar{AB}$

We observe that this perpendicular bisector of $\bar{AB}$ passes through the centre C of the circle.

Question: 8 Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?

Answer: The steps of constructions are: 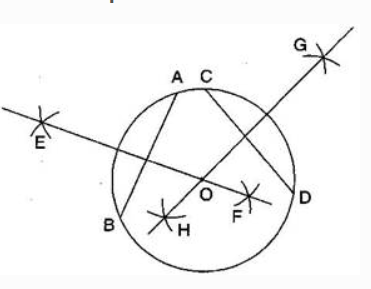1643783225321

(i) Draw the circle with O and radius 4 cm.

(ii) Draw any two chords $\bar{AB}$ and $\bar{CD }$ in this circle.

(iii) Taking A and B as centres and radius more than half AB, draw two arcs which intersect each other at E and F.

(iv) Join EF. Thus EF is the perpendicular bisector of chord $\bar{CD }$ .

(v) Similarly draw GH the perpendicular bisector of chord $\bar{CD }$ .

These two perpendicular bisectors meet at O, the centre of the circle.

Question:9 Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of $\overline{OA}$ and $\overline{OB}$ . Let them meet at P. Is PA = PB ?

Answer: The steps of constructions are:

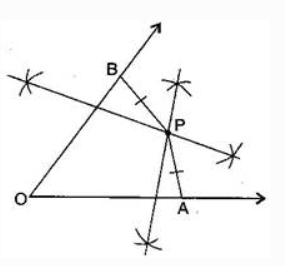
1643783250917

(i) Draw any angle with vertex O.

(ii) Take a point A on one of its arms and B on another such that

(iii) Draw perpendicular bisector of $\bar{OA}$ and $\bar{OB}$ .

(iv) Let them meet at P. Join PA and PB.

With the help of divider, we obtained that $\bar{PA} = \bar{PB}.$

NCERT Class 6 Maths Chapter 14 Practical Geometry Topic 14.5.4 Angles of Special Measures

Question: How will you construct a 15° angle?

Answer: First, we make $30^{\circ},$ and then its bisector.

The steps of constructions are:

1. Draw a ray OA.

2. Taking O as the center and any radius of your own choice, draw an arc cutting OA at B.

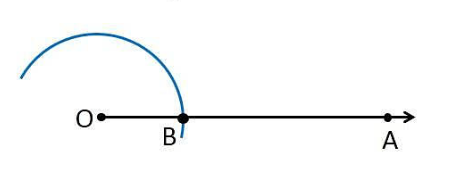
1657531206681

3. Now, taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc at point C.

4. Draw the ray OD passing through the C.

Thus, $\angle AOD = 60^{\circ}$

Now, we draw bisector of $\angle AOD$

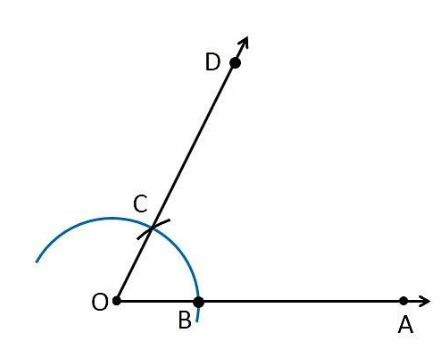
1657531394717

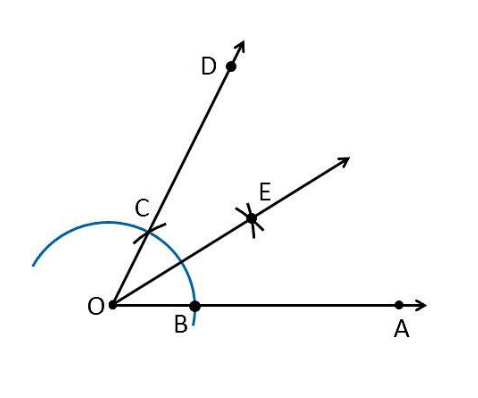
1657531423090

5. Taking C and D as the center, with radius more than $\frac{1}{2}CD$ , draw arcs intersecting at E.

6. Join OE.

Thus, $\angle AOE = 30^{\circ}$

Now, we draw the bisector of $\angle AOD$

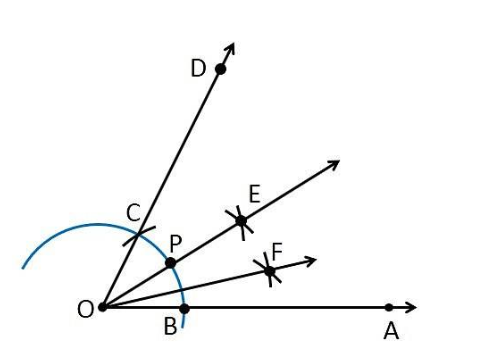
1657531454828

7. Mark point P where the ray OE intersects the arc.

8. Taking P and B as center, with having the radius more than $\frac{1}{2}PB$ , draw arcs intersecting at F.

9. Join OF

Thus, $\angle AOF = 15^{\circ}.$

Question: How will you construct a 150° angle?

Answer: Take a line segment, say, AB.

Choose a point C on it.

With center C, and radius BC, draw an arc.

With center B and radius BC, cut the previous arc at say DD.

$(\angle DCB=60^{\circ}\ because\ we\ just\ made\ CD=BC=BD )$

With center D, and radius BC draw an arc.

With center B and radius BC, cut this arc at, say, EE.

Then EC is the bisector of ∠BCD, and

Hence, $\angle BCE=30^{\circ}$

Then, $\angle ACE=180^{\circ} - \angle BCE=150^{\circ}$

Question: How will you construct a 45° angle?

Answer:

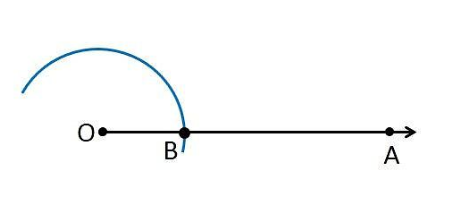
1. Draw a ray OA.

2. Taking O as center and any radius, draw an arc cutting OA at B.

1643783313354

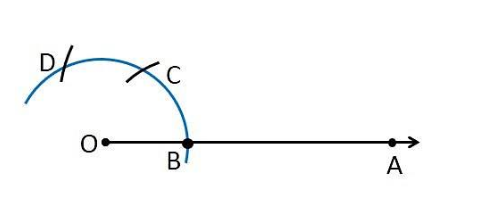
3. Now, taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc at point C.

4. With C as the center and the same radius, draw an arc cutting the arc at D.

1643783313039 \

5. With C and D as centers and radius more than 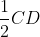$\frac{1}{2}CD$ , draw two arcs intersecting at P.

6. Join OP.

Thus, 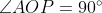$\angle AOP = 90^{\circ}$

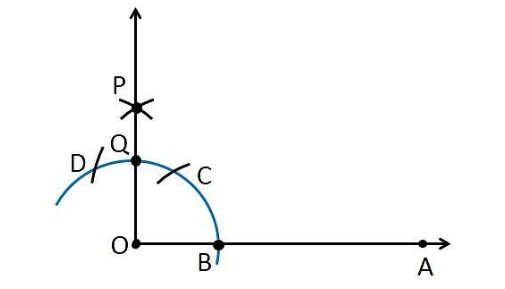
1643783313781

Now, we draw the bisector of 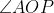$\angle AOP$

7. Let OP intersects the original arc at point Q.

8. Now, taking B and Q as centers, and radius greater than 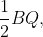$\frac{1}{2}BQ,$ draw two arcs intersecting at R.

9. Join OR.

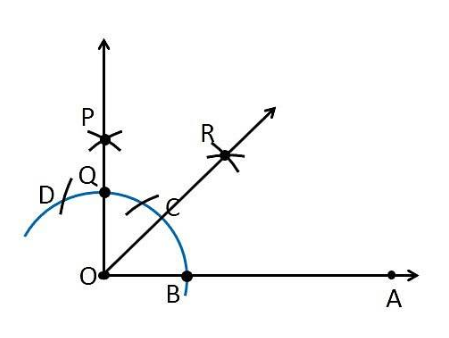
1643783314111

Thus, 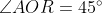$\angle AOR = 45^{\circ}$

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise: 14.6

Question: 1 Draw $\angle$ POQ of measure 75° and find its line of symmetry.

Answer:

1. Draw a ray OA.

1643783364905

2. Place the centre of the protractor on point O, and coincide line OA and Protractor line

3. Mark point B on 75 degrees.

4. Join OB

Therefore 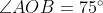$\angle AOB = 75^{\circ}$

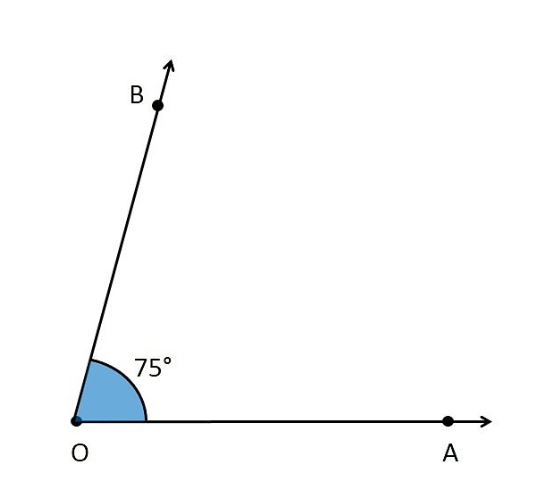
1643783365649

Now, we need to find its line of symmetry

that is, we need to find its bisector.

We follow these steps

1. Mark points C and D where the arc intersects OA and OB

1643783365879

2. Now, taking C and D as centres and with the radius more than 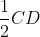$\frac{1}{2}CD$ , draw arcs to intersects each other.

3. Let them intersects at point E.

4. Join O and E.

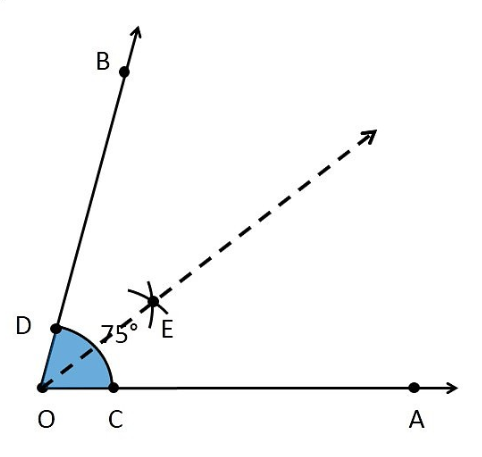
1643783366336

Therefore OE is the line of symmetry of 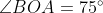$\angle BOA = 75^{\circ}$

Question: 2 Draw an angle of measure 147° and construct its bisector.

Answer: The steps of constructions are:

1. Draw a line OA.
2. Using protractor and centre 'O draw an angle AOB =147°.
3. Now taking 'O' as the centre and any radius draws an arc that intersects 'OA' and 'OB' at p and q.
4. Now take p and q as centres and radius more than half of PQ, draw arcs.
5. Both the arcs intersect at 'R'
6. Join 'OR' and produce it.
7. 'OR' is the required bisector of angle AOB. 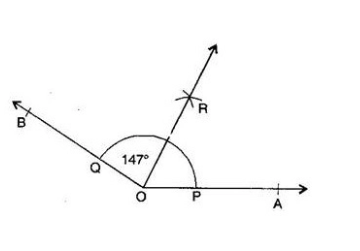1643783405828

Question: 3 Draw a right angle and construct its bisector.

Answer: The steps of construction:

(a) Draw a line PQ and take a point O on it.

(b) Taking O as the centre and convenient radius, draw an arc that intersects PQ at A and B.

(d) Join OC. Thus, ∠COQ is the required right angle.

(e) Taking B and E as centre and radius more than half of BE, draw two arcs that intersect each other at point D.

(f) Join OD. Thus, the OD bar is the required bisector of ∠COQ.

1643783431661

Question: 4 Draw an angle of measure 153° and divide it into four equal parts.

Answer: The steps of constructions are:

(a) Draw a ray OA.

(b) At O, with the help of a protractor, construct ∠AOB = 153 degrees.

(d) Again, draw OD as bisector of ∠AOC.

(e) Again, draw OE as bisector of,∠BOC.

(f) Thus, OC, OD, and OE divide ∠AOB into four equal parts.

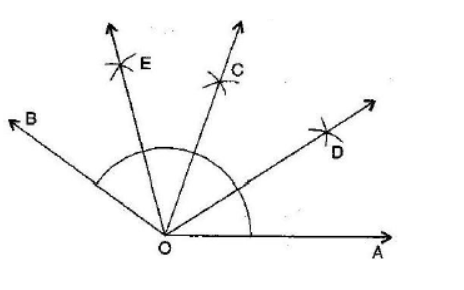
1643783457223

Question: 5(a) Construct with ruler and compasses, angles of following measures:

60 ^o

Answer: The steps of constructions are:

1. Draw a ray OA

2. Taking O as the centre and convenient radius, mark an arc, which intersects OA at P.

3. Taking P as the centre and the same radius, cut the previous arc at Q. Join OQ. Thus,∠BOA is the required angle of 60°

1643783491983

Question:5(b) Construct with ruler and compasses, angles of following measures:

30 ^o

Answer: The steps of constructions are:

1. Draw a ray OA.

2. Taking O as the centre and convenient radius, mark an arc, which intersects OA at P.

3. Taking P as the centre and the same radius, cut the previous arc at Q. Join OQ. Thus, ∠BOA is the required angle of 60°.

1643783531952

4. Put the pointer on P and mark an arc.

5. Put the pointer on Q and with the same radius, cut the previous arc at C. Thus, ∠COA is required angle of 30° 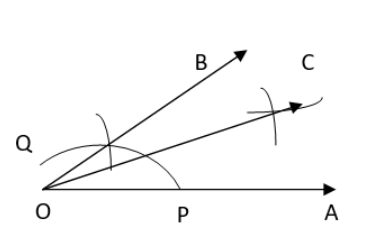1643783546175

Question: 5(c) Construct with ruler and compasses, angles of following measures:

90 ^o

Answer: The steps of constructions are:

1. Draw a ray OA

2. Taking O as the centre and convenient radius, mark an arc, which intersects OA at X.

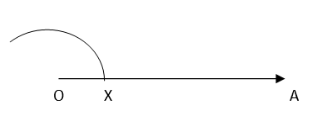
1643783585629

3. Taking X as the centre and the same radius, cut the previous arc at Y. Taking Y as the centre and the same radius, draw another arc intersecting the same arc at Z. 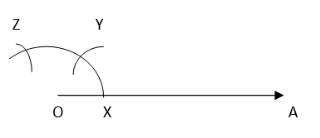1643783607939 4. Taking Y and Z as centres and the same radius, draw two arcs intersecting each other at S.

5. Join the OS. Thus, ∠SOA is a required angle of 90°

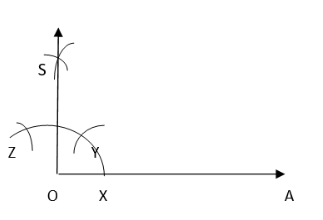
1643783627827

Question: 5(d) Construct with ruler and compasses, angles of following measures:

120 ^o

Answer: The steps of constructions are:

1. Draw a ray OA

2. Taking O as the centre and convenient radius, mark an arc, which intersects OA at P.

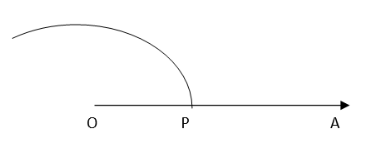
1643783661012

3. Taking P as the centre and same radius, cut the previous arc at Q. Taking Q as the centre and the same radius cut the arc at S. Join OS. Thus, ∠AOS is the required angle of 120°. 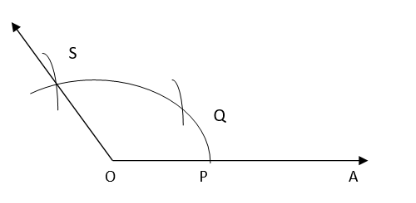1643783687173

Question:5(e) Construct with ruler and compasses, angles of following measures:

45 ^o

Answer: The steps of constructions are:

1. Draw a ray OA

2. Taking O as the centre and convenient radius, mark an arc, which intersects OA at X. 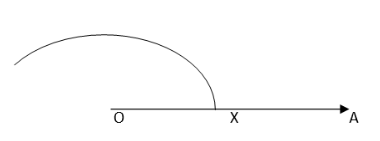1643783863071

3. Taking X as the centre and the same radius, cut the previous arc at Y. Taking Y as the centre and the same radius, draw another arc intersecting the same arc at Z.

4. Taking Y and Z as centres and the same radius, draw two arcs intersecting each other at S. Join OS. Thus, ∠SOA is a required angle of 90°. 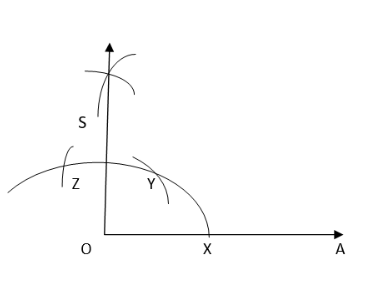1643783885127

5. Draw the bisector of SOA. Hence, ∠MOA = 45°

1643783929219

Question: 5(f) Construct with ruler and compasses, angles of following measures:

135 ^o

Answer: The steps of constructions are:

1. Draw a line PQ and take a point O on it.

2. Taking O as the centre and convenient radius, mark an arc, which intersects PQ at A and B.

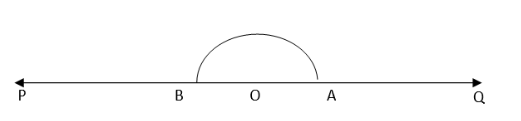
1643784000285

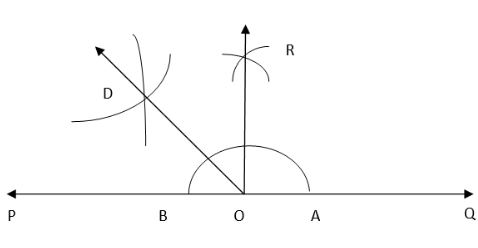
3. Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R. Join OR. Thus, ∠QOR = ∠POR = 90°. 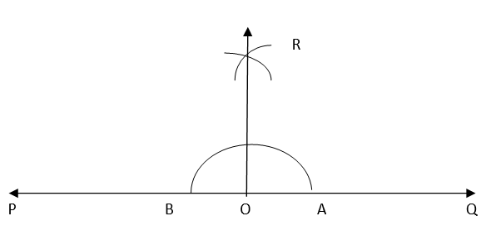1643784019617

4. Draw OD the bisector of ∠POR. Thus, ∠QOD is required angle of 135°

1643784039544

Question: 6 Draw an angle of measure 45° and bisect it.

Answer: The steps of constructions are:

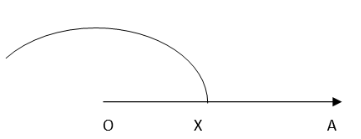
1. Draw a ray OA

2. Taking O as the centre and convenient radius, mark an arc, which intersects OA at X.

1643784073108

3. Taking X as a centre and the same radius, cut the previous arc at Y. Taking Y as the centre and the same radius, draw another arc intersecting the same arc at Z.

4. Taking Y and Z as centres and the same radius, draw two arcs intersecting each other at S. Join OS. Thus, ∠SOA is a required angle of 90°. 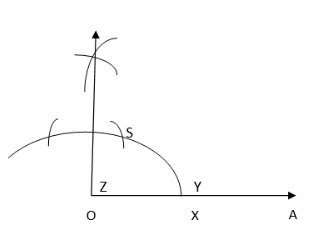1643784092564

5. Draw the bisector of ∠SOA. Hence, ∠MOA = 45°

6. Draw the bisector of ∠MOA. Hence, ∠NOA= 22.5 ⁰

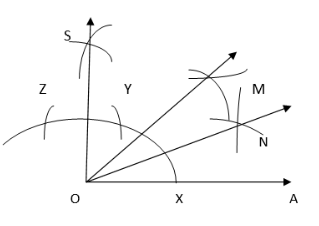
1643784112573

Question: 7 Draw an angle of measure 135° and bisect it.

Answer: The steps of constructions are:

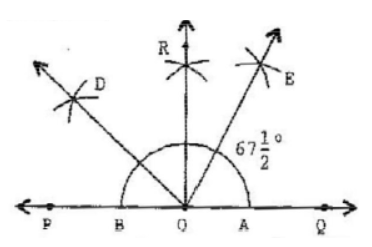
1643784150134

(a) Draw a line PQ and take a point O on it.

(b) Taking O as the centre and convenient radius, mark an arc, which intersects PQ at A and B.

(d) Join OR. Thus, ∠QOR = ∠POQ = 90 .

(e) Draw OD the bisector of ∠POR. Thus, ∠QOD is the required angle of 135.

(f) Now, draw OE as the bisector of ∠QOD=1/2 of 135=67.5

Question: 8 Draw an angle of 70 ^o . Make a copy of it using only a straight edge and compasses.

Answer: The steps of constructions are: 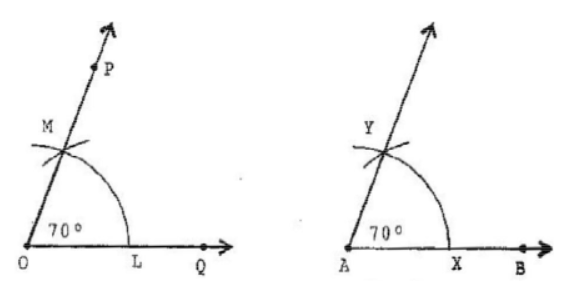1643784187334

(a) Draw an angle 70 degrees with a protractor, i.e., ∠POQ = 70 degrees

(b) Draw a ray AB.

(d) Use the same compasses, setting to draw an arc with A as the centre, cutting AB at X.

(e) Set your compasses setting to the length LM with the same radius.

(f) Place the compasses pointer at X and draw the arc to cut the arc drawn earlier at Y.

(g) Join AY. Thus, ∠YAX = 70 degree

Question: 9 Draw an angle of 40 ^o . Copy its supplementary angle.

Answer: 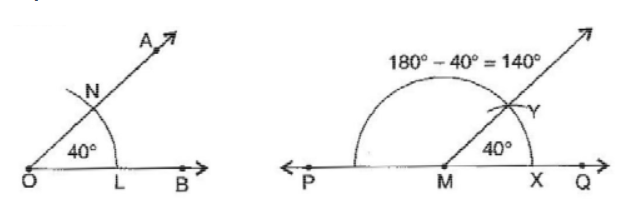1643784219376

The steps of constructions are:

(a) Draw an angle of 40 degrees with the help of a protractor, naming ∠ AOB.

(b) Draw a line PQ.

(d) Place the compasses at O and draw an arc to cut the rays of ∠AOB at L and N.

(e) Use the same compasses setting to draw an arc O as the centre, cutting MQ at X.

(f) Set your compasses to length LN with the same radius.

(g) Place the compasses at X and draw the arc to cut the arc drawn earlier Y.

(h) Join MY.

(i) Thus, < QMY = 40 degree and < PMY is supplementary of it.

Main Topics of NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

The Circle
Construction of a circle when its radius is known
A-Line Segment
Construction of a line segment of a given length
Constructing a copy of a given line segment
Perpendiculars
Perpendicular to a line through a point on it
Perpendicular to a line through a point not on it
The perpendicular bisector of a line segment
Angles
Constructing an angle of a given measure
Constructing a copy of an angle of an unknown measure
Bisector of an angle
Angles of special measures

Also Check

NCERT Books and NCERT Syllabus

NCERT Solutions for Class 6 Mathematics Chapter Wise

Chapters No.	Chapters Name
Chapter - 1	Knowing Our Numbers
Chapter - 2	Whole Numbers
Chapter - 3	Playing with Numbers
Chapter - 4	Basic Geometrical Ideas
Chapter - 5	Understanding Elementary Shapes
Chapter - 6	Integers
Chapter - 7	Fractions
Chapter - 8	Decimals
Chapter - 9	Data Handling
Chapter -10	Mensuration
Chapter -11	Algebra
Chapter -12	Ratio and Proportion
Chapter -13	Symmetry
Chapter -14	Practical Geometry

Key Features of NCERT Solutions for Class 6 Maths Chapter 14

Expertly Crafted Solutions: The NCERT Solutions for Chapter 14 are meticulously developed to offer clear and precise explanations for all the problems and concepts discussed in the chapter.

Conceptual Clarity: The solutions aim to improve students' conceptual understanding by simplifying complex topics and presenting them in a more comprehensible manner.

Comprehensive Coverage: The solutions cover all the essential topics and subtopics of Chapter 14, ensuring that students gain a thorough understanding of the entire chapter.

NCERT Solutions for Class 6 Subject Wise

NCERT Solutions for Class 6 Maths

NCERT Solutions for Class 6 Science

Benefits of NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry-

You will get NCERT Solutions for Class 6 very easily.
You will get some different ways to construct geometrical in this solution article.
There are some figures and images given in these solutions. It will help you in drawing geometrical figures easily.
In CBSE NCERT solutions for Class 6 Maths chapter 14 Practical Geometry, you will find that questions are explained with step-by-step to construct lines and geometrical figures with the help of compass and rulers. So you can understand easily
It is going to help you with your homework as well.

Happy learning!!!

Also Read

NCERT Solutions for Class 6 Science Chapter 3 Fibre to Fabric

NCERT Solutions for Class 6 Science Chapter 2 Components of Food

NCERT Solutions for Class 6 Science Chapter 1 Food Where Does It Come From

NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry

Articles

IGNOU BEd Answer Key 2025: Download OMR Sheet Here

Dec 13, 2024

TOSS Admission 2024-25: Apply for SSC & Inter TS Open School Admission @telanganaopenschool.org

Dec 13, 2024

IGNOU Registration 2025 (Statred), January Session, Last Date, Fess, Link, Apply Online

Dec 12, 2024

10 Ways To Think Straight, Without Bias

Dec 12, 2024

5 Apps To Help You Avoid Distractions, Become More Productive

Dec 12, 2024

Class 9 NSTSE 5-Year Analysis: Know Which Topics Get More Weightage And Why

Dec 12, 2024

How to Make APAAR ID via School, DigiLocker : Step-by-Step Guide

Dec 11, 2024

DBSE Admit Card 2025 for Class 10th and 12th

Dec 11, 2024

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Admit Card

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:02 December,2024 - 16 December,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Result

Exam Pattern

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry - Important Points

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry (Intext Questions and Exercise)

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.1

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.2

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.3

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.4

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise 14.5

NCERT Class 6 Maths Chapter 14 Practical Geometry Topic 14.5.4 Angles of Special Measures

NCERT Class 6 Maths Chapter 14 Practical Geometry Exercise: 14.6

Question: 1 Draw POQ of measure 75° and find its line of symmetry.

Main Topics of NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry

NCERT Solutions for Class 6 Mathematics Chapter Wise

Key Features of NCERT Solutions for Class 6 Maths Chapter 14

NCERT Solutions for Class 6 Subject Wise

Benefits of NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry-

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

National Institute of Open Schooling 12th Examination

National Means Cum-Merit Scholarship

Himachal Pradesh Board of Secondary Education 10th Examination

West Bengal Board 12th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app

Question: 1 Draw $\angle$ POQ of measure 75° and find its line of symmetry.