• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism

NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism

Edited By Vishal kumar | Updated on Sep 09, 2023 09:49 AM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions for Class 12 Physics Chapter 4 – Access and Download PDF for Free

NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism: If you're a Class 12 student in search of NCERT solutions, you've come to the right place. On this page, you'll find comprehensive class 12 physics chapter 4 ncert solutions from questions 1 to 28. Our class 12 physics ch 4 ncert solutions have been meticulously crafted by subject experts, providing detailed explanations for each step. Also, you have the option to download these solutions in PDF format, enabling you to work on them offline as well.

This Story also Contains
  1. NCERT Solutions for Class 12 Physics Chapter 4 – Access and Download PDF for Free
  2. NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism
  3. Class 12 Physics ch 4 Exercise solutions
  4. Moving Charges And Magnetism Class 12 Main Topics-
  5. NCERT Solutions Subject Wise
  6. Importance of NCERT solutions for class 12 physics chapter 4 moving charges and magnetism in exams:
NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism
NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism

A moving charge in a magnetic field can produce a force and a current-carrying conductor in a uniform magnetic field will experience a force. The solutions of NCERT Class 12 Physics Chapter 4 Moving Charges and Magnetism cover problems based on these two basic concepts. Class 12 chapter 4 physics ncert solutions will help you to boost the concepts studied in this chapter of the NCERT syllabus.

Two main laws discussed in the NCERT chapter Moving charges and Magnetism Class 12 are Ampere's law and Biot-savant law. Based on these laws many problems are discussed in CBSE NCERT solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism. The galvanometer is discussed in Moving charges and Magnetism Class 12 in detail with its working principle. NCERT Solutions for Class 12 Physics Chapter 4 Moving charges and Magnetism helps students for solving homework problems.

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

The right-hand thumb rule, Flemings right-hand rule and Flemings left-hand rule are three important concepts of Moving charges and Magnetism chapter of NCERT textbook. The problems related to finding the directions can be solved using these three rules or by using the concepts of vectors. The NCERT solutions for Class 12 Physics also helps in preparing for competitive exams like NEET and JEE Mains.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Free download class 12 chapter 4 physics ncert solutions PDF for CBSE exam.

NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism

Download PDF


Class 12 Physics ch 4 Exercise solutions

1. A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?

Answer :

The magnitude of the magnetic field at the centre of a circular coil of radius r carrying current I is given by,

|B|=\frac{\mu _{0}I}{2r}

For 100 turns, the magnitude of the magnetic field will be,

|B|=100\times \frac{\mu _{0}I}{2r}

|B|=100\times \frac{4\pi \times 10^{-7}\times 0.4}{2\times 0.08} (current=0.4A, radius = 0.08m, permeability of free space = 4 \pi \times 10 -7 TmA -1 )

=3.14\times10^{-4}T

2. A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire?

Answer:

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

|B|=\frac{\mu _{0}I}{2\pi r}

In this case

|B|=\frac{4\pi \times 10^{-7}\times 35}{2\pi\times 0.2}=3.5\times 10^{-5}T (current=35A, distance= 0.2m, permeability of free space = 4 \pi \times 10 -7 TmA -1 )

3. A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.

Answer:

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

|B|=\frac{\mu _{0}I}{2\pi r}

In this case

|B|=\frac{4\pi \times 10^{-7}\times 50}{2\pi\times 2.5} (current=50A, distance= 2.5m, permeability of free space = 4 \pi \times 10 -7 TmA -1 )

\\=4\times10^{-6}T

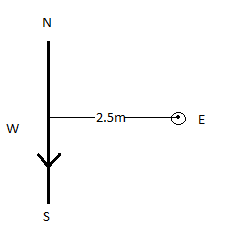
1643264249758The current is going from the North to South direction in the horizontal plane and the point lies to the East of the wire. Applying Maxwell's right-hand thumb rule we can see that the direction of the magnetic field will be vertically upwards.

4. A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?

Answer:

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

|B|=\frac{\mu _{0}I}{2\pi r}

In this case (current=35A, distance= 0.2m, permeability of free space = 4 \pi \times 10 -7 TmA -1 )

|B|=\frac{4\pi \times 10^{-7}\times 90}{2\pi\times 1.5}=1.2\times10^{-5} T

The current in the overhead power line is going from the East to West direction and the point lies below the power line. Applying Maxwell's right-hand thumb rule we can see that the direction of the magnetic field will be towards the South.

5. What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of 30 \degree with the direction of a uniform magnetic field of 0.15 T?

Answer:

The magnetic force on an infinitesimal current-carrying conductor in a magnetic field is given by \vec{dF}=I\vec{dl}\times \vec{B} where the direction of vector dl is in the direction of flow of current.

For a straight wire of length l in a uniform magnetic field, the Force equals to

\\\vec{F}=\int_{0}^{l}I\vec{dl}\times \vec{B}\\ |\vec{F}|=BIlsin\theta

In the given case the magnitude of force per unit length is equal to

|F| = 0.15 \times 8 \times sin30 o (I=8A, B=0.15 T, \theta =30 o )

=0.6 Nm -1

6. A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?

Answer:

For a straight wire of length l in a uniform magnetic field, the Force equals to

\\\vec{F}=\int_{0}^{l}I\vec{dl}\times \vec{B}\\ |\vec{F}|=BIlsin\theta

In the given case the magnitude of the force is equal to

|F| = 0.27 \times 10 \times 0.03 \times sin90 o (I=10A, B=0.27 T, \theta =90 o )

=0.081 N

The direction of this force depends on the orientation of the coil and the current-carrying wire and can be known using the Flemings Left-hand rule.

7. Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.

Answer:

The magnitude of magnetic field at a distance r from a long straight wire carrying current I is given by,

|B|=\frac{\mu _{0}I}{2\pi r}

In this case the magnetic field at a distance of 4.0 cm from wire B will be

|B|=\frac{4\pi \times 10^{-7}\times 5}{2\pi\times 0.04} (I=5 A, r=4.0 cm)

\\=2.5\times10^{-5} T

The force on a straight wire of length l carrying current I in a uniform magnetic field B is given by

F=BIlsin\theta , where \theta is the angle between the direction of flow of current and the magnetic field.

The force on a 10 cm section of wire A will be

F=2.5\times10^{-5}\times8\times0.1 \times sin90^\circ (B=2.5 T, I=8 A, l = 10 cm, \theta =90 o )

F=2\times10^{-5} N

8. A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.

Answer:

The magnitude of the magnetic field at the centre of a solenoid of length l, total turns N and carrying current I is given by

B=\frac{\mu _{o}NI}{l} , where \mu _{o} is the permeability of free space.

In the given question N= number of layers of winding \times number of turns per each winding

N=5 \times 400=2000

I=8.0 A

l=80 cm

B=\frac{4\pi \times 10^{-7}\times 2000\times 8}{0.8}

\\B=2.51\times10^{-2} T

9. A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30 \degree with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?

Answer:

The magnitude of torque experienced by a current-carrying coil in a magnetic field is given by

\tau =nBIAsin\theta

where n = number of turns, I is the current in the coil, A is the area of the coil and \theta is the angle between the magnetic field and the vector normal to the plane of the coil.

In the given question n = 20, B=0.8 T, A=0.1 \times 0.1=0.01 m 2 , I=12 A, \theta =30 o

\tau =20\times 0.8\times 12\times 0.01\times sin30^{o}

=0.96 Nm

The coil, therefore, experiences a torque of magnitude 0.96 Nm.

10 (a) Two moving coil meters, M_1 and M_2 have the following particulars:


R_1 = 10 \Omega , N_1 = 30,\\\\ A_1 = 3.6 \times 10^{-3} m^2, B_1 = 0.25 T\\\\ R_2 = 14 \Omega , N_2 = 42,\\\\ A_2 = 1.8 \times 10^{-3} m^2, B_2 = 0.50 T
(The spring constants are identical for the two meters).
Determine the ratio of current sensitivity of M_2\ and \ \ M_1

Answer:

The torque experienced by the moving coil M 1 for a current I passing through it will be equal to \tau =B_{1}A_{1}N_{1}I

The coil will experience a restoring torque proportional to the twist \phi

\phi k=B_{1}A_{1}N_{1}I

The current sensitivity is therefore \frac{B_{1}A_{1}N_{1}}{k}

Similarly, for the coil M 2, current sensitivity is \frac{B_{2}A_{2}N_{2}}{k}

Their ratio of current sensitivity of coil M 2 to that of coil M 1 is, therefore, \frac{B_{2}A_{2}N_{2}}{B_{1}A_{1}N_{1}}

=\frac{0.5\times 1.8\times 10^{-3}\times 42 }{0.25\times 3.6\times 10^{-3}\times 30}=1.4

10.(b) Two moving coil meters, M_1 and M_2 have the following particulars:


R_1 = 10 \Omega , N_1 = 30,\\\\ A_1 = 3.6 \times 10^{-3} m^2, B_1 = 0.25 T\\\\ R_2 = 14 \Omega , N_2 = 42,\\\\ A_2 = 1.8 \times 10^{-3} m^2, B_2 = 0.50 T
(The spring constants are identical for the two meters).

Determine the ratio of voltage sensitivity of M_2 and M_1

Answer:

The torque experienced by the moving coil M 1 for a current I passing through it will be equal to \tau =B_{1}A_{1}N_{1}I

The coil will experience a restoring torque proportional to the twist \phi

\phi k=B_{1}A_{1}N_{1}I

we know V=IR

Therefore, \phi k=\frac{B_{1}A_{1}N_{1}V}{R_{1}}

Voltage sensitivity of coil M 1 = \frac{B_{1}A_{1}N_{1}}{kR_{1}}

Similarly for coil M 2 Voltage sensitivity = \frac{B_{2}A_{2}N_{2}}{kR_{2}}

Their ratio of voltage sensitivity of coil M 2 to that of coil M 1

=\frac{B_{2}A_{2}N_{2}R_{1}}{B_{1}A_{1}N_{1}R_{2}}

=1.4\times \frac{10}{14}

\\=1

11) In a chamber, a uniform magnetic field of 6.5 G ( 1G = 10 ^{-4}T ) is maintained. An electron is shot into the field with a speed of 4.8 \times 10 ^ 6 ms ^{-1} normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit. (e = 1.5 \times 10 ^{-19} C, m_e = 9.1\times 10^{-31} kg)

Answer:

The magnetic force on a moving charged particle in a magnetic field is given by \vec{F_{B}}=q\vec{V}\times \vec{B}

Since the velocity of the shot electron is perpendicular to the magnetic field, there is no component of velocity along the magnetic field and therefore the only force on the electron will be due to the magnetic field and will be acting as a centripetal force causing the electron to move in a circular path. (if the initial velocity of the electron had a component along the direction of the magnetic field it would have moved in a helical path)

Magnetic field(B)= 6.5 G ( 1G = 10 ^{-4}T )

Speed of electron(v)= 4.8 \times 10 ^ 6 ms ^{-1}

Charge of electron= -1.6\times 10^{-19}C

Mass of electron= 9.1\times 10^{-31}kg

The angle between the direction of velocity and the magnetic field = 90 o

Since the force due to the magnetic field is the only force acting on the particle,

\\\frac{mV^{2}}{r}=q\vec{V}\times \vec{B}\\ \frac{mV^{2}}{r}=|qVBsin\theta| \\ r=|\frac{mV}{qBsin\theta }|

r=\frac{9.1\times 10^{-31}\times 4.8\times 10^{6}}{1.6\times 10^{-19}\times 6.5\times 10^{-4}}=4.2 cm

12) In Exercise 4.11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain

Answer:

In exercise 4.11 we saw r=\frac{eB}{mv}

Time taken in covering the circular path once(time period (T))= \frac{2\pi r}{v} =\frac{2\pi m}{eB}

Frequency, \nu =\frac{1}{T}=\frac{eB}{2\pi m}

From the above equation, we can see that this frequency is independent of the speed of the electron.

\nu =\frac{1.6\times 10^{-19}\times 4.8\times 10^{6}}{2\pi \times 9.1\times 10^{-31}}=18.2 MHz

13 (a) A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60 \degree with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.

Answer:

Number of turns in the coil(n)=30

The radius of the circular coil(r)=8.0 cm

Current flowing through the coil=6.0 A

Strength of magnetic field=1.0 T

The angle between the field lines and the normal of the coil=60 o

The magnitude of the counter-torque that must be applied to prevent the coil from turning would be equal to the magnitude of the torque acting on the coil due to the magnetic field.

\\\tau =nBIAsin\theta\\ \tau = 30\times 1\times 6\times \pi \times (0.08)^{2}\times sin60^{o}

=3.13 Nm

A torque of magnitude 3.13 Nm must be applied to prevent the coil from turning.

13 b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)

Answer:

From the relation \tau =nBIAsin\theta we can see that the torque acting on the coil depends only on the area and not its shape, therefore, the answer won't change if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area.


NCERT solutions for moving charges and magnetism additional exercise:

14) Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

Answer:

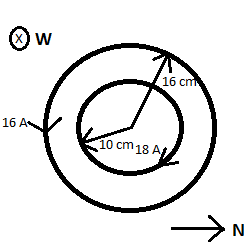
1643264303579

Using the right-hand thumb rule we can see that the direction of the magnetic field due to coil X will be towards the east direction and that due to coil Y will be in the West direction.

We know the magnetic field at the centre of a circular loop of radius r carrying current I is given by

B=\frac{\mu _{o}I}{2r}

\\B_{x}=\frac{n_{x}\mu _{o}I_{x}}{2r_{x}}\\ \\B_{x}=\frac{20\times 4\pi \times 10^{-7}\times 16}{2\times 0.16}

\\B_x=4\pi\times 10^{-4}T (towards East)

\\B_{y}=\frac{n_{y}\mu _{o}I_{y}}{2r_{y}}\\ \\B_{y}=\frac{25\times 4\pi \times 10^{-7}\times 18}{2\times 0.1}

\\B_y=9\pi \times10^{-4}T (towards west)

The net magnetic field at the centre of the coils,

B net =B y - B x

=1.57 \times 10 -3 T

The direction of the magnetic field at the centre of the coils is towards the west direction.

15) A magnetic field of 100 G ( 1G = 10 ^{-4}) T is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10 ^{-3} m^2 The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000\: \: turns\: \: m ^{-1} . Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.

Answer:

Strength of the magnetic field required is 100 G ( 1G = 10 ^{-4}) T

B=\mu _{o}nI

nI=\frac{B}{\mu _{o}}

nI \\=\frac{100\times 10^{-4}}{4\pi \times 10^{-7}}\\ \\=7957.74 \approx 8000

Therefore keeping the number of turns per unit length and the value of current within the prescribed limits such that their product is approximately 8000 we can produce the required magnetic field.

e.g. n=800 and I=10 A.

16.(a) For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

B = \frac{\mu _0 IR^2N}{2 ( x^2 + R^2 )^{3/2}}

Show that this reduces to the familiar result for the field at the centre of the coil.

Answer:

For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

B = \frac{\mu _0 IR^2N}{2 ( x^2 + R^2 )^{3/2}}

For finding the field at the centre of coil we put x=0 and get the familiar result

B = \frac{\mu _0 IN}{2R}

16. (b) For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

B = \frac{\mu _0 IR^2N}{2 ( x^2 + R^2 )^{3/2}}

Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
B = 0.72 \frac{\mu _0 NI}{R} approximately.

Answer:

Let a point P be at a distance of l from the midpoint of the centres of the coils.

The distance of this point from the centre of one coil would be R/2+l and that from the other would be R/2-l.

The magnetic field at P due to one of the coils would be

. B_{1}= \frac{\mu _0 IR^2N}{2 ( (R/2+l)^2 + R^2 )^{3/2}}

The magnetic field at P due to the other coil would be

B_{2}= \frac{\mu _0 IR^2N}{2 ( (R/2-l)^2 + R^2 )^{3/2}}

Since the direction of current in both the coils is same the magnetic fields B 1 and B 2 due to them at point P would be in the same direction

B net =B 1 +B 2

\\B_{net}= \frac{\mu _0 IR^2N}{2 ( (R/2-l)^2 + R^2 )^{3/2}}+\frac{\mu _0 IR^2N}{2 ( (R/2+l)^2 + R^2 )^{3/2}}\\ \\B_{net}= \frac{\mu _0 IR^2N}{2}\left [ ( (R/2-l)^2 + R^2 )^{-3/2} + ( (R/2+l)^2 + R^2 )^{-3/2}\right ]\\ \\B_{net}= \frac{\mu _0 IR^2N}{2}\left [ ( \frac{R^{2}}{4}-Rl+l^{2} + R^2 )^{-3/2} + ( \frac{R^{2}}{4}+Rl+l^{2} + R^2 )^{-3/2}\right ]\\ \\B_{net}= \frac{\mu _0 IR^2N}{2}\left [ ( \frac{5R^{2}}{4}-Rl+l^{2} )^{-3/2} + ( \frac{5R^{2}}{4}+Rl+l^{2} )^{-3/2}\right ]\\

\\B_{net}= \frac{\mu _0 IR^2N}{2}\times (\frac{5R^{2}}{4})^{-3/2}\left [ ( 1-\frac{4l}{5R}+\frac{4l^{2}}{5R^{2}} )^{-3/2} + ( 1+\frac{4l}{5R}+\frac{4l^{2}}{5R^{2}} )^{-3/2}\right ]\\

Since l<<R we can ignore term l 2 /R 2

\\B_{net}= \frac{\mu _0 IN}{2R}\times (\frac{5}{4})^{-3/2}\left [ ( 1-\frac{4l}{5R} )^{-3/2} + ( 1+\frac{4l}{5R} )^{-3/2}\right ]\\

\\B_{net}= \frac{\mu _0 IN}{2R}\times (\frac{4}{5})^{3/2}\left [ 1+\frac{6l}{5R} + 1-\frac{6l}{5R} \right ]\\

\\B_{net}= \frac{\mu _0 IN}{2R}\times (\frac{4}{5})^{3/2}\times 2

\\B_{net}= 0.715\frac{\mu _0 IN}{R}\approx 0.72\frac{\mu _0 IN}{R}

Since the above value is independent of l for small values it is proved that about the midpoint the Magnetic field is uniform.

17.(a) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field outside the toroid

Answer:

Outside the toroid, the magnetic field will be zero.

17.(b) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field inside the core of the toroid?

Answer:

The magnetic field inside the core of a toroid is given by

B=\frac{\mu _{o}NI}{l}

Total number of turns(N)=3500

Current flowing in toroid =11 A

Length of the toroid, l=

\\l=2\pi \left (\frac{ r_{1}+r_{2}}{2} \right )\\ \\l=\pi ( r_{1}+r_{2})\\ \\l=\pi (0.25+0.26)\\ \\l=0.51\pi (r 1 =inner radius=25 cm, r 2 =outer radius=26 cm)

B=\frac{4\pi \times 10^{-7}\times 3500\times 11}{0.51\pi }=0.031 T

17.(c) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field in the empty space surrounded by the toroid?

Answer:

The magnetic field in the empty space surrounded by the toroid is zero.

18. (a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

Answer:

The charged particle is not deflected by the magnetic field even while having a non zero velocity, therefore, its initial velocity must be either parallel or anti-parallel to the magnetic field i.e. It's velocity is either towards the east or the west direction.

18 b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?

Answer:

Yes, its final speed will be equal to the initial speed if it has not undergone any collision as the work done by the magnetic field on a charged particle is always zero because it acts perpendicular to the velocity of the particle.

18 c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.

Answer:

The electron would experience an electrostatic force towards the north direction, therefore, to nullify its force due to the magnetic field must be acting on the electron towards the south direction. By using Fleming's left-hand rule we can see that the force will be in the north direction if the magnetic field is in the vertically downward direction.

Explanation:

The electron is moving towards the east and has a negative charge therefore q\vec{V} is towards the west direction, Force will be towards south direction if the magnetic field is in the vertically downward direction as \vec{F}=q\vec{V}\times \vec{B}

19 (a) An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field is transverse to its initial velocity

Answer:

(a) The electron has been accelerated through a potential difference of 2.0 kV.

Therefore K.E of electron = 1.6 \times 10^{-19} \times 2000 =3.2 \times10^{-16} J

\\\frac{1}{2}mv^{2}=3.2\times 10^{-16}\\ \\v=\sqrt{\frac{2\times 3.2\times 10^{-16}}{9.1\times 10^{-31}}}\\ v=2.67\times 10^{7}\ ms^{-1}

Since the electron initially has velocity perpendicular to the magnetic field it will move in a circular path.

The magnetic field acts as a centripetal force. Therefore,

\\\frac{mv^{2}}{r}=evB\\ r=\frac{mv}{eB}\\ r=\frac{9.1\times 10^{-31}\times 2.67\times 10^{7}}{1.6\times 10^{-19}\times 0.15}=1.01mm

19. (b) An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field makes an angle of 30 \degree with the initial velocity.

Answer:

The electron has been accelerated through a potential difference of 2.0 kV.

Therefore K.E of electron = 1.6 \times 10 -19 \times 2000=3.2 \times 10 -16 J

\\\frac{1}{2}mv^{2}=3.2\times 10^{-16}\\ \\v=\sqrt{\frac{2\times 3.2\times 10^{-16}}{9.1\times 10^{-31}}}\\ v=2.67\times 10^{7}\ ms^{-1}

The component of velocity perpendicular to the magnetic field is

\\v_{p}=vsin30^{o}\\ v_{p}=1.33\times 10^{7}\ ms^{-1}

The electron will move in a helical path of radius r given by the relation,

\\\frac{mv^{2}_{p}}{r}=ev_{p}B\\ r=\frac{mv_{p}}{eB}\\ r=\frac{9.1\times 10^{-31}\times 1.33\times 10^{7}}{1.6\times 10^{-19}\times 0.15}

r=5m

r=5 \times 10 -4 m

r=0.5 mm

The component of velocity along the magnetic field is

\\v_{t}=vcos30^{o}\\ v_{t}=2.31\times 10^{7}\ ms^{-1}

The electron will move in a helical path of pitch p given by the relation,

\\p=\frac{2\pi r}{v_{p}}\times v_{t}\\ p=\frac{2\pi \times 5\times 10^{-4}}{1.33\times 10^{7}}\times 2.31\times 10^{7}

p=5.45 \times 10 -3 m

p=5.45 mm

The electron will, therefore, move in a helical path of radius 5 mm and pitch 5.45 mm.

20 A magnetic field set up using Helmholtz coils (described in Exercise 4.16) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV
enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 \times 10 ^{-5} V m ^{-1} , make a simple guess as to what the beam contains. Why is the answer not unique?

Answer:

\\qE=qvB\\ E=vB (i)

Let the beam consist of particles having charge q and mass m.

After being accelerated through a potential difference V its velocity can be found out by using the following relation,

\\\frac{1}{2}mv^{2}=qV\\ \\v=\sqrt{\frac{2qV}{m}} (ii)

Using the value of v from equation (ii) in (i) we have

\\E=B\sqrt{\frac{2qV}{m}}\\ \frac{q}{m}=\frac{E^{2}}{2VB^{2}}\\ \frac{q}{m}=\frac{(9\times 10^{-5})^{2}}{2\times 15\times 10^{3}\times (0.75)^{2}}=4.8\times 10^{-13}

21. (a) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

Answer:

In order for the tension in the wires to be zero the force due to the magnetic field must be equal to the gravitational force on the rod.

mg=BIl

mass of rod=0.06 g

length of rod=0.45m

the current flowing through the rod=5 A

\\B=\frac{mg}{Il}\\ B=\frac{0.06\times 9.8}{5\times 0.45}\\ B=0.261\ T

A magnetic field of strength 0.261 T should be set up normal to the conductor in order that the tension in the wires is zero

21.(b) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before?
(Ignore the mass of the wires.) g = 9.8 m s ^{-2}

Answer:

If the direction of the current is reversed the magnetic force would act in the same direction as that of gravity.

Total tension in wires(T)=Gravitational force on rod + Magnetic force on rod

\\T=mg+BIl\\ \\T=0.06\times 9.8+0.261\times 5\times 0.45\\ \\T=1.176\ N

The total tension in the wires will be 1.176 N.

22. The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?

Answer:

Since the distance between the wires is much smaller than the length of the wires we can calculate the Force per unit length on the wires using the following relation.

F=\frac{\mu _{o}I_{1}I_{2}}{2\pi d}

Current in both wires=300 A

Distance between the wires=1.5 cm

Permeability of free space=4 \pi \times 10 -7 TmA -1

F=\frac{4\pi \times 10^{-7}\times 300\times 300}{2\pi \times 0.015}

F=1.2 Nm -1

23.(a) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire intersects the axis,

Answer:

The length of wire inside the magnetic field is equal to the diameter of the cylindrical region=20.0 cm=0.2 m.

Magnetic field strenth=1.5 T.

Current flowing through the wire=7.0 A

The angle between the direction of the current and magnetic field=90 o

Force on a wire in a magnetic field is calculated by relation,

\\F=BIlsin\theta \\ F=1.5\times 7\times 0.2

F=2.1 N

This force due to the magnetic field inside the cylindrical region acts on the wire in the vertically downward direction.

23.(b) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire is turned from N-S to northeast-northwest direction,

Answer:

Magnetic field strenth=1.5 T.

Current flowing through the wire=7.0 A

The angle between the direction of the current and magnetic field=45 o

The radius of the cylindrical region=10.0 cm

The length of wire inside the magnetic field, \\l=\frac{2r}{sin\theta }\\

Force on a wire in a magnetic field is calculated by relation,

\\F=BIlsin\theta \\ \\F=1.5\times 7\times \frac{2\times 0.1}{sin45^{o}}\times sin45^{o}

F=2.1 N

This force due to the magnetic field inside the cylindrical region acts on the wire in the vertically downward direction.

This force will be independent of the angle between the wire and the magnetic field as we can see in the above case.

Note: There is one case in which the force will be zero and that will happen when the wire is kept along the axis of the cylindrical region.

23 c) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire in the N-S direction is lowered from the axis by a distance
of 6.0 cm?

Answer:

The wire is lowered by a distance d=6cm.

In this case, the length of the wire inside the cylindrical region decreases.

Let this length be l.

\\(\frac{l}{2})^{2}+d^{2}=r^{2}\\ \\(\frac{l}{2})^{2}=0.1^{2}-0.06^{2}\\ \\(\frac{l}{2})^{2}=0.01-0.0036\\ \\\\(\frac{l}{2})^{2}=0.0064\\ \\\frac{l}{2}=0.08\\ \\l=0.16m

\\F=BIlsin\theta \\ F=1.5\times 7\times 0.16

F=1.68 N

This force acts in the vertically downward direction.

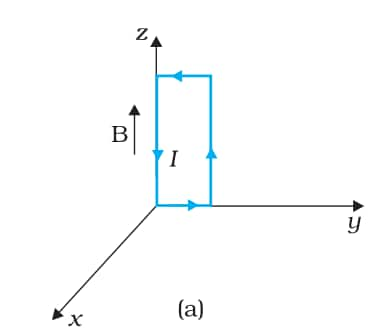
24.(a) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

1594189909926

Answer:

The magnetic field is

\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}

Current in the loop=12 A

Area of the loop = length \times breadth

A=0.1 \times 0.05

A=0.005 m 2

\vec{A}=0.005\ m^{2}\hat{i}

\\\vec{\tau }=I\vec{A}\times \vec{B}\\ \\\vec{\tau }=12\times 0.005\hat{i}\times 0.3\hat{k}\\ \\\vec{\tau }=-0.018\hat{j}

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-y direction. The force on the loop is zero.

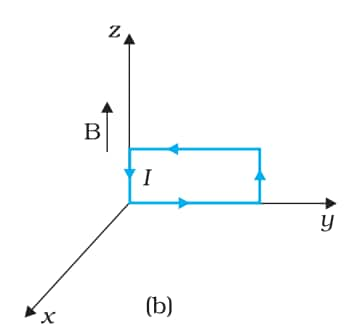
24.(b) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

1594190067991

Answer:

The magnetic field is

\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}

Current in the loop=12 A

Area of the loop = length \times breadth

A=0.1 \times 0.05

A=0.005 m 2

\vec{A}=0.005\ m^{2}\hat{i} (same as that in the last case)

\\\vec{\tau }=I\vec{A}\times \vec{B}\\ \\\vec{\tau }=12\times 0.005\hat{i}\times 0.3\hat{k}\\ \\\vec{\tau }=-0.018\hat{j}

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-y direction. The force on the loop is zero. This was exactly the case in 24. (a) as well.

24 (c). A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

1594190068868

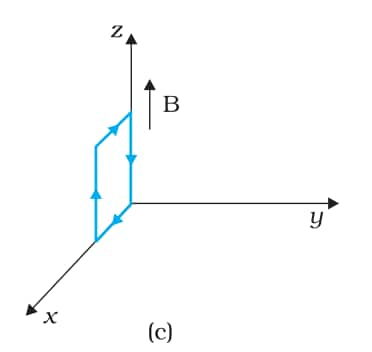
Answer:

The magnetic field is

\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}

Current in the loop=12 A

Area of the loop = length \times breadth

A=0.1 \times 0.05

A=0.005 m 2

\vec{A}=-0.005\ m^{2}\hat{j}

\\\vec{\tau }=I\vec{A}\times \vec{B}\\ \\\vec{\tau }=12\times- 0.005\hat{j}\times 0.3\hat{k}\\ \\\vec{\tau }=-0.018\hat{i}

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-x-direction. The force on the loop is zero.

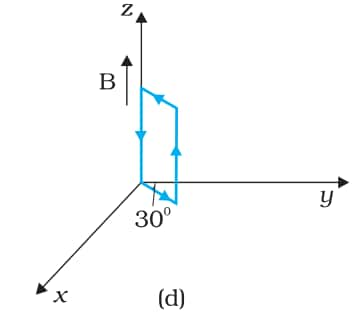
24 (d) . A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?


1594190161239

Answer:

The magnetic field is

\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}

Current in the loop=12 A

Area of the loop = length \times breadth

A=0.1 \times 0.05

A=0.005 m 2

\vec{A}=0.005\ m^{2}(-\frac{\hat{i}}{2}+\frac{\sqrt{3}}{2}\hat{j})

\\\vec{\tau }=I\vec{A}\times \vec{B}\\ \\\vec{\tau }=12\times 0.005(-\frac{\hat{i}}{2}+\frac{\sqrt{3}}{2}\hat{j})\times 0.3\hat{k}\\ \\\vec{\tau }=-0.018(\frac{\hat{i}}{2}+\frac{\sqrt{3}}{2}\hat{j})

The torque on the loop has a magnitude of 0.018 Nm and at an angle of 240 o from the positive x-direction. The force on the loop is zero.

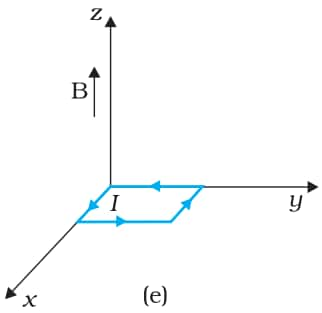
24. (e) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

1594190217628

Answer:

The magnetic field is

\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}

Current in the loop=12 A

Area of the loop = length \times breadth

A=0.1 \times 0.05

A=0.005 m 2

\vec{A}=0.005\ m^{2}\hat{k}

Since the area vector is along the direction of the magnetic field the torque on the loop is zero. The force on the loop is zero.

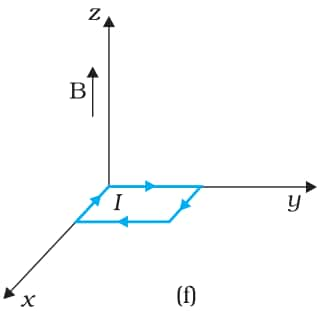
24 (f) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

1594190291878

Answer:

The magnetic field is

\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}

Current in the loop=12 A

Area of the loop = length \times breadth

A=0.1 \times 0.05

A=0.005 m 2

\vec{A}=-0.005\ m^{2}\hat{k}

Since the area vector is in the opposite direction of the magnetic field the torque on the loop is zero. The force on the loop is zero.

The force on the loop in all the above cases is zero as the magnetic field is uniform

25. (a) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the total torque on the coil,

Answer:

As we know the torque on a current-carrying loop in a magnetic field is given by the following relation

\\\vec{\tau }=I\vec{A}\times \vec{B}\\

It is clear that the torque, in this case, will be 0 as the area vector is along the magnetic field only.

25. (b) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, total force on the coil.

Answer:

The total force on the coil will be zero as the magnetic field is uniform.

25 (c) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10 ^{-5} m^2 , and the free electron density in copper is given to be about 10 ^{29} m^{-3} .)

Answer:

The average force on each electron in the coil due to the magnetic field will be eV d B where V d is the drift velocity of the electrons.

The current is given by

I=neAV_{d}

where n is the free electron density and A is the cross-sectional area.

\\V_{d}=\frac{I}{neA}\\ \\V_{d}=\frac{5}{10^{29}\times 1.6\times 10^{-19}\times 10^{-5}}

Vd=3.125\times10^{-5} ms^{-1}

The average force on each electron is

F=eV_dB

F=1.6\times10^{-19}\times3.125\times10^{-5}\times00.1

F=5\times10^{-25} N

26. A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with an appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? g = 9.8 m s ^{-2}

Answer:

The magnetic field inside the solenoid is given by

B=\mu _{0}nI

n is number of turns per unit length

n=\frac{3\times 300}{0.6}

n=1500 m -1

Current in the wire I w = 6 A

Mass of the wire m = 2.5 g

Length of the wire l = 2 cm

The windings of the solenoid would support the weight of the wire when the force due to the magnetic field inside the solenoid balances weight of the wire

BI_wl=mg

\\B=\frac{mg}{I_{w}l}\\ \\\mu _{0}nI=\frac{mg}{I_{w}l}\\ I=\frac{mg}{I_{w}l\mu _{0}n}\\ I=\frac{2.5\times 10^{-3}\times 9.8}{6\times 0.02\times 4\pi \times 10^{-7}\times 1500}\\ I=108.37\ A

Therefore a current of 108.37 A in the solenoid would support the wire.

27. A galvanometer coil has a resistance of 12 \Omega and the metre shows full scale deflection for a current of 3 mA. How will you convert the metre into a voltmeter of range 0 to 18 V?

Answer:

The galvanometer can be converted into a voltmeter by connecting an appropriate resistor of resistance R in series with it.

At the full-scale deflection current(I) of 3 mA the voltmeter must measure a Voltage of 18 V.

The resistance of the galvanometer coil G = 12 \Omega

I \times (R+G)=18 V

R=\frac{18}{3\times 10^{-3}}-12

R=6000-12

\\=5988\Omega

The galvanometer can be converted into a voltmeter by connecting a resistor of resistance 5988\Omega in series with it.

28. A galvanometer coil has a resistance of 15 \Omega and the metre shows full scale deflection for a current of 4 mA. How will you convert the metre into an ammeter of range 0 to 6 A?

Answer:

The galvanometer can be converted into an ammeter by connecting an appropriate resistor of resistance R in series with it.

At the full-scale deflection current(I) of 4 mA, the ammeter must measure a current of 6 A.

The resistance of the galvanometer coil is G = 15 \Omega

Since the resistor and galvanometer coil are connected in parallel the potential difference is the same across them.

IG=(6-I)R

\\R=\frac{IG}{6-I}\\ \\R=\frac{4\times 10^{-3}\times 15}{6-4\times 10^{-3}}\\ R\approx 0.01\Omega

The galvanometer can be converted into an ammeter by connecting a resistor of resistance 0.01\Omega in parallel with it.

Understanding moving charges and magnetism class 12 ncert solutions is like building the foundation of a tall building. It helps you do well in your regular school exams (like the bricks at the bottom) and is also crucial for clearing tough entrance exams like JEE and NEET (like the support structure that holds up the building). So, it's important for both your regular studies and future career goals.

Class 12 physics chapter 4 exercise solutions: Important Formulas and Diagrams

Important formulas of physics chapter 4 class 12 ncert solutions are listed below:

  • Force Applied To A Moving Charge

\vec{F}=q(\vec{v}\times \vec{B})

  • Biot-Savart’s Law

1643017915027

\vec{dB}=\frac{\mu_0I}{4\pi}\frac{\vec{dl}\times\vec{r}}{r^3}

  • Ampere Circuital Law

\int B.dl=\mu_0I

  • Cyclotron

Centripetal force=magnetic Lorentz force1643017933694

Cyclotron frequency =1643017916003

Cyclotron angular frequency = 1643017927366

Maximum kinetic energy of the particle =1643017925548

Moving Charges And Magnetism Class 12 Main Topics-

The following topics are covered in ch 4 Physics Class 12:

  • Magnetic Force- The force on a moving charge in a uniform magnetic field and also a force on a current-carrying conductor in a magnetic field are discussed in chapter 4 Physics Class 12. Some questions based on these concepts are discussed in the Class 12 Physics Chapter 4 NCERT solutions. For example questions, 5, 11, 18 and 23 of NCERT solutions for Class 12 Physics Chapter 4 uses the concepts of force on a charge/conductor in a uniform magnetic field.

  • Motion in a magnetic field- This part of Moving charges and Magnetism Class 12 discusses the trajectory of a charge in a magnetic field. Questions based on this are discussed in the Moving Charges and Magnetism solutions given above.

  • The motion of combined electric and magnetic field- The motion of charge in the presence of both electric and magnetic fields and also the topic cyclotron is discussed in this portion of Class 12 NCERT Physics.

  • Biot-Savart law, Amperes circuital law- These two laws and their applications are discussed in Physics chapter 4 Class 12.

    Other topics discussed in class 12 physics chapter 4 question answer are solenoid, toroid, the force between parallel conductors, torques on a rectangular loop in a magnetic field, the angular momentum of the electron and the concept of moving coil galvanometer and conversion of galvanometer to ammeter and voltmeter. Understanding the formulas and concepts in these topics are important to get a better idea while solving the problems.

Key Features of moving charges and magnetism class 12 ncert solutions

  1. Comprehensive Coverage: The class 12 physics chapter 4 exercise solutions cover all the topics and questions presented in the Class 12 Physics Chapter "Moving Charges and Magnetism."

  2. Step-by-Step Explanations: Each class 12 physics chapter 4 question answer provides detailed step-by-step explanations, helping students understand complex concepts.

  3. Clarity and Simplicity: The physics chapter 4 class 12 ncert solutions are written in clear and simple language, making it easier for students to comprehend the content.

  4. Practice Questions: Exercise questions are included to help students practice and assess their understanding.

  5. Exam Preparation: These class 12 physics ch 4 exercise solutions aid students in preparing effectively for board exams and competitive exams like JEE and NEET.

  6. Foundation for Advanced Topics: The concepts covered in this chapter are essential for more advanced topics in physics and electrical engineering.

  7. Free Access: These solutions are available for free, ensuring accessibility to all students.

These features make the Class 12 "Moving Charges and Magnetism" solution a valuable resource for students, facilitating their success in exams and future studies.

Also Check NCERT Books and NCERT Syllabus here:

NCERT Exemplar Class 12 Solutions

NCERT Solutions For Class 12 Physics Chapter - Wise

NCERT Solutions Subject Wise

Importance of NCERT solutions for class 12 physics chapter 4 moving charges and magnetism in exams:

As CBSE board exam is concerned, the solutions of NCERT Class 12 Physics chapter 4 Moving Charges and Magnetism is important. In 2019 CBSE board exam 12 % of questions are asked from chapter 4 and 5. Same questions discussed in the chapter 4 Physics Class 12 NCERT solutions can be expected in the board exams. NCERT Exemplar Class 12 Physics Solutions

Frequently Asked Questions (FAQs)

1. What is the weightage of NCERT physics chapter 4 for CBSE board exam

The chapter Moving Charges and Magnetism have 8 to 10 percentage weightage. The questions asked from the chapter can be of a numerical, derivation or theory questions. CBSE board follows NCERT Syllabus. To practice problems refer to NCERT text book, NCERT syllabus and previous year board papers of Class 12 Physics.

2. Can I skip the chapter moving charges for NEET preperation

No, you can not skip it. Since from NCERT Class 12 Physics chapter 4 you can expect 2 questions for NEET exam. 

3. Can I crack JEE Main questions from Moving Charges and Magnetism just by knowing the equations in the NCERT

No, you have to practise more questions for doing well in JEE main exams. The  questions of Moving Charges and Magnetism need a good base of vectors and a thorough understanding of concepts 

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

Gujarat Board Secondary School Certificate Examination

Application Date:22 October,2024 - 30 November,2024

Gujarat Board Higher Secondary School Certificate

Application Date:24 October,2024 - 02 December,2024

Haryana Board of Secondary Education 10th Examination

Application Date:04 November,2024 - 03 December,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 812 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
IBM
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
Board Exam Date Sheet 2025 Live: ICSE, ISC, CBSE, MP time table out; BSEB routine soon
November 26, 2024 - 10:18 PM IST
Board exam dates 2025: CBSE, CISCE, UP, MP, Maharashtra, TN time table out; state-wise updates
November 25, 2024 - 08:42 PM IST
Board Exam Date Sheet 2025: CBSE, UPMSP, MPBSE, Class 10, 12 board exam dates out; BSEB, CGBSE schedules soon
November 22, 2024 - 10:04 PM IST
CBSE Date Sheet 2025 (Out) Live: Class 10, 12 board exam time table at cbse.gov.in; syllabus, sample papers
November 21, 2024 - 09:30 PM IST
CBSE Board Exam Date Sheet 2025 (OUT) Live: CBSE Classes 10, 12 time table out 86 days before exams start
November 20, 2024 - 11:17 PM IST
CBSE Class 12 board exam date sheet 2025 out; exams from February 15 to April 4
November 20, 2024 - 09:56 PM IST
When will CBSE Board exam 2025 date sheet be released for Class 10, 12?
November 20, 2024 - 03:58 PM IST

Stay up-to date with CBSE Class 12th News

Back to top