Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 8.2 Class 12 Maths Chapter 8 - Application of Integrals

NCERT Solutions for Exercise 8.2 Class 12 Maths Chapter 8 - Application of Integrals

Edited By Ramraj Saini | Updated on Dec 03, 2023 10:26 PM IST | #CBSE Class 12th

NCERT Solutions For Class 12 Maths Chapter 8 Exercise 8.2

NCERT Solutions for Exercise 8.2 Class 12 Maths Chapter 8 Application of Integrals are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. NCERT solutions for Class 12 Maths chapter 8 exercise 8.2 is similar to the exercise 8.1. Also it has linkages with the previous chapter. Exercise 8.2 Class 12 Maths consists of questions related to areas bounded by two different curves. NCERT solutions for Class 12 Maths chapter 8 exercise 8.2 can be solved easily if the concept is understood from initial few questions. All other questions have the same concept used. Similar questions which are in this exercise are asked in Physics also, hence this exercise becomes more important.

This Story also Contains
  1. NCERT Solutions For Class 12 Maths Chapter 8 Exercise 8.2
  2. Access NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2
  3. Application of Integrals Class 12 Chapter 8 Exercise: 8.2
  4. More About NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2
  5. Also Read| Application of Integrals Class 12 Notes
  6. Benefits of NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2
  7. Key Features Of NCERT Solutions for Exercise 8.2 Class 12 Maths Chapter 8
  8. Also see-
  9. NCERT Solutions Subject Wise
  10. Subject Wise NCERT Exemplar Solutions

12th class Maths exercise 8.2 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

PTE Registrations 2024

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer!

Apply

Access NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2

Download PDF

Application of Integrals Class 12 Chapter 8 Exercise: 8.2

Question: 1 Find the area of the circle \small 4x^2+4y^2=9 which is interior to the parabola \small x^2=4y .

Answer:

The area bounded by the circle \small 4x^2+4y^2=9 and the parabola \small x^2=4y .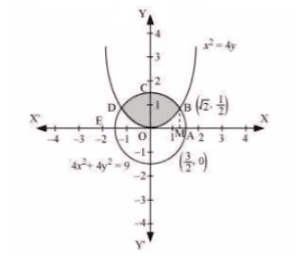
15947278183451594727815379
By solving the equation we get the intersecting point D(-\sqrt{2},\frac{1}{2}) and B(\sqrt{2},\frac{1}{2})
So, the required area (OBCDO)=2 times the area of (OBCO)
Draw a normal on the x-axis (M = \sqrt{2},0 )


Thus the area of OBCO = Area of OMBCO - Area of OMBO

\\\int_{0}^{\sqrt{2}}\sqrt{\frac{(9-4x^2)}{4}}dx-\int_{0}^{\sqrt{2}}{\frac{x^2}{4}}dx\\ =\frac{1}{2}\int_{0}^{\sqrt{2}}\sqrt{9-4x^2}-\frac{1}{4}\int_{0}^{\sqrt{2}}x^2dx\\ =\frac{1}{4}[x\sqrt{9-4x^2}+\frac{9}{2}\sin^{-1}\frac{2x}{3}]_0^{\sqrt{2}}-\frac{1}{4}[\frac{x^3}{3}]_0^{\sqrt{2}}\\ =\frac{1}{4}[\sqrt{2}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}]-\frac{1}{12}(\sqrt{2})^3\\ =\frac{\sqrt{2}}{12}+\frac{9}{8}\sin^{-1}\frac{2\sqrt{2}}{3}\\ =\frac{1}{2}(\frac{\sqrt{2}}{6}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3})
S0, total area =
\\=2\times \frac{1}{2}(\frac{\sqrt{2}}{6}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3})\\ =\frac{\sqrt{2}}{6}+\frac{9}{4}\sin^{-1}\frac{2\sqrt{2}}{3}

Question:2 Find the area bounded by curves \small (x-1)^2+y^2=1 and \small x^2+y^2=1 .

Answer:

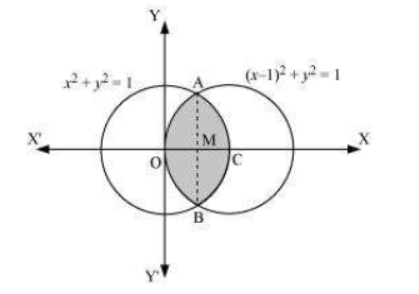1654758558749 Given curves are \small (x-1)^2+y^2=1 and \small x^2+y^2=1

Point of intersection of these two curves are

A = \left ( \frac{1}{2},\frac{\sqrt3}{2} \right ) and B = \left ( \frac{1}{2},-\frac{\sqrt3}{2} \right )

We can clearly see that the required area is symmetrical about the x-axis

Therefore,

Area of OBCAO = 2 \times Area of OCAO

Now, join AB such that it intersects the x-axis at M and AM is perpendicular to OC

Coordinates of M = \left ( \frac{1}{2},0 \right )

Now,

Area OCAO = Area OMAO + Area CMAC

=\left [ \int_{0}^{\frac{1}{2}}\sqrt{1-(x-1)^2}dx +\int_{\frac{1}{2}}^{1}\sqrt{1-x^2}dx \right ]
=\left [ \frac{x-1}{2}\sqrt{1-(x-1)^2}+\frac{1}{2}\sin^{-1}(x-1) \right ]_{0}^{\frac{1}{2}}+\left [ \frac{x}{2}+\frac{1}{2}\sin^{-1}x \right ]_{\frac{1}{2}}^{1}

=\left [- \frac{1}{4}\sqrt{1-(-\frac{1}{2})^2}+\frac{1}{2}\sin^{-1}(\frac{1}{2}-1)-0-\frac{1}{2}\sin^{-1}(-1) \right ]+\left [ 0+\frac{1}{2}\sin^{-1}(1)- \frac{1}{4}\sqrt{1-\left ( \frac{1}{2} \right )^2}-\frac{1}{2}\sin^{-1}\left ( \frac{1}{2} \right )\right ]
=\left [ -\frac{\sqrt3}{8}+\frac{1}{2}\left ( -\frac{\pi}{6} \right )-\frac{1}{2}\left ( -\frac{\pi}{2} \right ) \right ]+\left [ \frac{1}{2}\left ( \frac{\pi}{2} \right ) -\frac{\sqrt3}{8}-\frac{1}{2}\left ( \frac{\pi}{6} \right )\right ]
= \left [ -\frac{\sqrt3}{8}+\frac{\pi}{6} \right ]+\left [ \frac{\pi}{6}-\frac{\sqrt3}{8} \right ]
=2 \left [ -\frac{\sqrt3}{8}+\frac{\pi}{6} \right ]
Now,
Area of OBCAO = 2 \times Area of OCAO

=2\times 2 \left [ -\frac{\sqrt3}{8}+\frac{\pi}{6} \right ]
=\frac{2\pi}{3}-\frac{\sqrt3}{2}

Therefore, the answer is \frac{2\pi}{3}-\frac{\sqrt3}{2}

Question: 3 Find the area of the region bounded by the curves \small y=x^2+2,y=x,x=0 and \small x=3 .

Answer:

The area of the region bounded by the curves,

\small y=x^2+2,y=x,x=0 and \small x=3 is represented by the shaded area OCBAO as

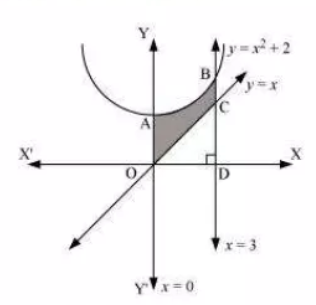
1654758611010

Then, Area OCBAO will be = Area of ODBAO - Area of ODCO

which is equal to

\int_0^3(x^2+2)dx - \int_0^3x dx

= \left ( \frac{x^3}{3}+2x \right )_0^3 -\left ( \frac{x^3}{2} \right )_0^3

= \left [ 9+6 \right ] - \left [ \frac{9}{2} \right ] = 15-\frac{9}{2} = \frac{21}{2}units.

Question: 4 Using integration find the area of region bounded by the triangle whose vertices are \small (-1,0),(1,3) and \small (3,2) .

Answer:

So, we draw BL and CM perpendicular to x-axis.

Then it can be observed in the following figure that,

Area(\triangle ACB) = Area (ALBA)+Area(BLMCB) - Area (AMCA)

We have the graph as follows:

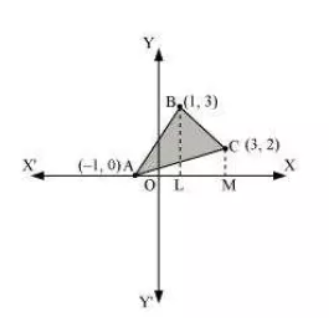
1654758688421

Equation of the line segment AB is:

y-0 = \frac{3-0}{1+1}(x+1) or y = \frac{3}{2}(x+1)

Therefore we have Area of ALBA

=\int_{-1}^1 \frac{3}{2}(x+1)dx =\frac{3}{2}\left [ \frac{x^2}{2}+x \right ]_{-1}^1

=\frac{3}{2}\left [ \frac{1}{2}+1-\frac{1}{2}+1 \right ] =3units.

So, the equation of line segment BC is

y-3 = \frac{2-3}{3-1}(x-1) or y= \frac{1}{2}(-x+7)

Therefore the area of BLMCB will be,

=\int_1^3 \frac{1}{2}(-x+7)dx =\frac{1}{2}\left [ -\frac{x^2}{2}+7x \right ]_1^3

= \frac{1}{2}\left [ -\frac{9}{2}+21+\frac{1}{2}-7 \right ] =5units.

Equation of the line segment AC is,

y-0 = \frac{2-0}{3+1}(x+1) or y = \frac{1}{2}(x+1)

Therefore the area of AMCA will be,

=\frac{1}{2}\int_{-1}^3 (x+1)dx =\frac{1}{2}\left [ \frac{x^2}{2}+x \right ]_{-1}^3

=\frac{1}{2}\left ( \frac{9}{2}+3-\frac{1}{2}+1 \right ) = 4units.

Therefore, from equations (1), we get

The area of the triangle \triangle ABC =3+5-4 =4units.

Question:5 Using integration find the area of the triangular region whose sides have the equations \small y=2x+1,y=3x+1 and \small x=4 .

Answer:

The equations of sides of the triangle are y=2x+1, y =3x+1,\ and\ x=4 .

ON solving these equations, we will get the vertices of the triangle as A(0,1),B(4,13),\ and\ C(4,9)

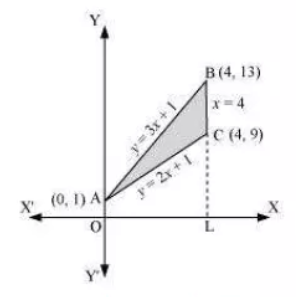
1654758730701

Thus it can be seen that,

Area (\triangle ACB) = Area (OLBAO) -Area (OLCAO)

= \int_0^4 (3x+1)dx -\int_0^4(2x+1)dx

= \left [ \frac{3x^2}{2}+x \right ]_0^4 - \left [ \frac{2x^2}{2}+x \right ]_0^4

=(24+4) - (16+4) = 28-20 =8units.

Question:6 Choose the correct answer.

Smaller area enclosed by the circle \small x^2+y^2=4 and the line \small x+y=2 is

(A) \small 2(\pi -2) (B) \small \pi -2 (C) \small 2\pi -1 (D) \small 2(\pi +2)

Answer:

So, the smaller area enclosed by the circle, x^2+y^2 =4 , and the line, x+y =2 , is represented by the shaded area ACBA as

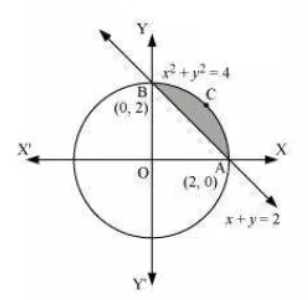
1654758775744

Thus it can be observed that,

Area of ACBA = Area OACBO - Area of (\triangle OAB)

=\int_0^2 \sqrt{4-x^2} dx -\int_0^2 (2-x)dx

= \left ( \frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}\sin^{-1}{\frac{x}{2}} \right )_0^2 - \left ( 2x -\frac{x^2}{2} \right )_0^2

= \left [ 2.\frac{\pi}{2} \right ] -[4-2]

= (\pi -2) units.

Thus, the correct answer is B.

Question:7 Choose the correct answer.

Area lying between the curves \small y^2=4x and \small y=2x is

(A) \small \frac{2}{3} (B) \small \frac{1}{3} (C) \small \frac{1}{4} (D) \small \frac{3}{4}

Answer:

The area lying between the curve, \small y^2=4x and \small y=2x is represented by the shaded area OBAO as

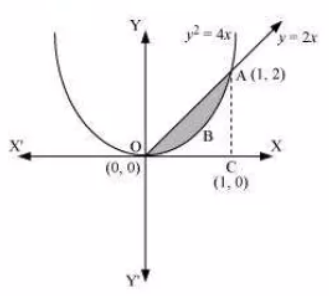
1654758937961

The points of intersection of these curves are O(0,0) and A (1,2) .

So, we draw AC perpendicular to x-axis such that the coordinates of C are (1,0).

Therefore the Area OBAO = Area(\triangle OCA) -Area (OCABO)

=2\left [ \frac{x^2}{2} \right ]_0^1 - 2\left [ \frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right ]_0^1

=\left | 1-\frac{4}{3} \right | = \left | -\frac{1}{3} \right | = \frac{1}{3} units.

Thus the correct answer is B.



More About NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2

The NCERT Class 12 Maths chapter application of Integrals mainly deals with the finding out of an area bounded by two curves. Exercise 8.2 Class 12 Maths is an extension of last exercise only. Hence before doing NCERT solutions for Class 12 Maths chapter 8 exercise 8.2 one should complete the exercise 8.1.

Also Read| Application of Integrals Class 12 Notes

Benefits of NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2

  • The Class 12th Maths chapter 8 exercise has 3 exercises in total maily dealing with the application of integrals.
  • These Class 12 Maths chapter 8 exercise 8.2 solutions are helpful in solving the questions in the upcoming exercise also.
  • NCERT solutions for Class 12 Maths chapter 8 exercise 8.2 provides mostly moderate to difficult level of questions.
50+ Entrance Exams for 10+2 Students Must Not Miss
Download this ebook to learn about 50+ entrance exams for 12th students to get admission to the best colleges for undergraduates.
Download EBook

Key Features Of NCERT Solutions for Exercise 8.2 Class 12 Maths Chapter 8

  • Comprehensive Coverage: The solutions encompass all the topics covered in ex 8.2 class 12, ensuring a thorough understanding of the concepts.
  • Step-by-Step Solutions: In this class 12 maths ex 8.2, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
  • Accuracy and Clarity: Solutions for class 12 ex 8.2 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
  • Conceptual Clarity: In this 12th class maths exercise 8.2 answers, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
  • Inclusive Approach: Solutions for ex 8.2 class 12 cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
  • Relevance to Curriculum: The solutions for class 12 maths ex 8.2 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Happy learning!!!


Frequently Asked Question (FAQs)

1. How many questions are there in exercise 8.2 Class 12 Maths ?

Total of 7 questions are there in exercise 8.2 Class 12 Maths.

2. Which applications are mentioned in this exercise ?

Area under two curves are discussed in this chapter mainly. 

3. Is this chapter very important for Board exams ?

Yes, this chapter holds good weightage so it is important to cover comprehensively. 

4. What is the difficulty level of this exercise 8.2 ?

Moderate to difficult level of questions are asked from this exercise. 

5. Mention some of the topics discussed in this chapter ?

Maily area and at higher level volume etc. are discussed in this. 

6. How many exercises does this chapter include ?

3 exercises are there in this chapter including miscellaneous exercise.

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

International General Knowledge Olympiad

Exam Date:19 September,2024 - 19 September,2024

Unified Cyber Olympiad

Exam Date:20 September,2024 - 20 September,2024

National Institute of Open Schooling 10th examination

Exam Date:20 September,2024 - 07 October,2024

National Institute of Open Schooling 12th Examination

Exam Date:20 September,2024 - 07 October,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

You can use them people also used problem

Read Complete Answer
Divyan 06 August,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

The Medhavi National Scholarship Program, under the Human Resources & Development Mission (HRDM), offers financial assistance to meritorious students through a scholarship exam. To be eligible, candidates must be between 16 and 40 years old as of the last date of registration and have at least passed the 10th grade from a recognized board. Higher qualifications, such as 11th/12th grade, graduation, post-graduation, or a diploma, are also acceptable.

To apply, download the Medhavi App from the Google Play Store, sign up, and read the detailed notification about the scholarship exam. Complete the registration within the app, take the exam from home using the app, and receive your results within two days. Following this, upload the necessary documents and bank account details for verification. Upon successful verification, the scholarship amount will be directly transferred to your bank account.

The scholarships are categorized based on the marks obtained in the exam: Type A for those scoring 60% or above, Type B for scores between 50% and 60%, and Type C for scores between 40% and 50%. The cash scholarships range from Rs. 2,000 to Rs. 18,000 per month, depending on the exam and the marks obtained.

Since you already have a 12th-grade qualification with 84%, you meet the eligibility criteria and can apply for the Medhavi Scholarship exam. Preparing well for the exam can increase your chances of receiving a higher scholarship.

Read Complete Answer
Yuvan 01 September,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
I have completed my 12th with arts cbse. I want to repeat my 12th with pcmb. How to become a private candidate and what are deadline to be able to appear in 2025 exam?

Hello student,

If you are planning to appear again for class 12th board exam with PCMB as a private candidate here is the right information you need:

  • No school admission needed! Register directly with CBSE. (But if you want to attend the school then you can take admission in any private school of your choice but it will be waste of money)
  • You have to appear for the 2025 12th board exams.
  • Registration for class 12th board exam starts around September 2024 (check CBSE website for exact dates).
  • Aim to register before late October to avoid extra fees.
  • Schools might not offer classes for private students, so focus on self-study or coaching.

Remember , these are tentative dates based on last year. Keep an eye on the CBSE website ( https://www.cbse.gov.in/ ) for the accurate and official announcement.

I hope this answer helps you. If you have more queries then feel free to share your questions with us, we will be happy to help you.

Good luck with your studies!

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Registrations 2024
PTE Registrations 2024
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer!

JEE Main high scoring chapters and topics
JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE sample paper 2024-25, marking scheme out for skill education subjects
September 02, 2024 - 12:13 PM IST
CBSE to overhaul internal assessment system, develop framework with British Council
August 28, 2024 - 04:58 PM IST
65 lakh students didn't clear Class 10, 12 board exams last year: Education ministry
August 21, 2024 - 10:24 PM IST
CBSE Compartment Result 2024: Marks verification, answer book photocopy, revaluation dates out
August 06, 2024 - 12:37 PM IST
CBSE Class 12 compartment results 2024 declared at cbseresults.nic.in; 29.78% pass
August 02, 2024 - 04:46 PM IST
CBSE best, Kerala board worst in curriculum, infrastructure: NCERT PARAKH report
July 30, 2024 - 04:48 PM IST
Assign 40% weightage to Class 12 exam in final result; have ‘on-demand exams’: NCERT PARAKH report
July 29, 2024 - 07:54 PM IST

Stay up-to date with CBSE Class 12th News

Back to top