NCERT Solutions for Class 10 Maths Chapter 5 Exercise 5.3 - Arithmetic Progressions

Q1 (i) Find the sum of the following APs: $\small 2,7,12,...,$ to $\small 10$ terms.

Answer:

Given series $\small 2,7,12,...,$ to $\small 10$ terms

Here, $a = 2 \ and \ n = 10$ and $d = a_2-a_1=7-2=5$

Now, we know that

$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S = \frac{10}{2}\left \{ 2\times 2 +(10-1)5\right \}$

$\Rightarrow S = 5\left \{ 4 +45\right \}$

$\Rightarrow S = 5\left \{ 49\right \}$

$\Rightarrow S =245$

Therefore, the sum of AP $\small 2,7,12,...,$ to $\small 10$ terms is 245

Q1 (ii) Find the sum of the following APs: $\small -37,-33,-29,...,$ to $\small 12$ terms.

Answer:

Given series $\small -37,-33,-29,...,$ to $\small 12$ terms.

Here, $a = -37 \ and \ n = 12$ and $d = a_2-a_1=-33-(-37)=4$

Now, we know that

$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S = \frac{12}{2}\left \{ 2\times (-37) +(12-1)4\right \}$

$\Rightarrow S = 6\left \{ -74 +44\right \}$

$\Rightarrow S = 5\left \{ -30\right \}$

$\Rightarrow S =-180$

Therefore, the sum of AP $\small -37,-33,-29,...,$ to $\small 12$ terms. is -180

Q1 (iii) Find the sum of the following APs: $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms.

Answer:

Given series $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms..

Here, $a = 0.6 \ and \ n = 100$ and $d = a_2-a_1=1.7-0.6=1.1$

Now, we know that

$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S = \frac{100}{2}\left \{ 2\times (0.6) +(100-1)(1.1)\right \}$

$\Rightarrow S = 50\left \{ 1.2 +108.9\right \}$

$\Rightarrow S = 50\left \{ 110.1\right \}$

$\Rightarrow S =5505$

Therefore, the sum of AP $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms. is 5505

Q1 (iv) Find the sum of the following APs: $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms.

Answer:

Given series $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms.

Here, $a = \frac{1}{15} \ and \ n = 11$ and $d = a_2-a_1=\frac{1}{12}-\frac{1}{15}= \frac{5-4}{60}= \frac{1}{60}$

Now, we know that

$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S = \frac{11}{2}\left \{ 2\times \frac{1}{15} +(11-1)(\frac{1}{60})\right \}$

$\Rightarrow S = \frac{11}{2}\left \{ \frac{2}{15} +\frac{1}{6}\right \}$

$\Rightarrow S = \frac{11}{2}\left \{ \frac{9}{30}\right \}$

$\Rightarrow S =\frac{99}{60}= \frac{33}{20}$

Therefore, the sum of AP $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms. is $\frac{33}{20}$

Q2 (i) Find the sums given below: $\small 7+10\frac{1}{2}+14+...+84$

Answer:

Given series $\small 7+10\frac{1}{2}+14+...+84$

First we need to find the number of terms

Here, $a = 7 \ and \ a_n = 84$ and $d = a_2-a_1=\frac{21}{2}-7= \frac{21-14}{2}= \frac{7}{2}$

Let suppose there are n terms in the AP

Now, we know that

$a_n = a+(n-1)d$

$\Rightarrow 84 = 7 + (n-1)\frac{7}{2}$

$\Rightarrow \frac{7n}{2}= 77+\frac{7}{2}$

$\Rightarrow n = 23$

Now, we know that

$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S = \frac{23}{2}\left \{ 2\times7 +(23-1)(\frac{7}{2})\right \}$

$\Rightarrow S = \frac{23}{2}\left \{ 14 +77\right \}$

$\Rightarrow S = \frac{23}{2}\left \{ 91\right \}$

$\Rightarrow S =\frac{2093}{2}=1046\frac{1}{2}$

Therefore, the sum of AP $\small 7+10\frac{1}{2}+14+...+84$ is $1046\frac{1}{2}$

Q2 (ii) Find the sums given below: $\small 34+32+30+...+10$

Answer:

Given series $\small 34+32+30+...+10$

First we need to find the number of terms

Here, $a = 34 \ and \ a_n = 10$ and $d = a_2-a_1=32-34=-2$

Let suppose there are n terms in the AP

Now, we know that

$a_n = a+(n-1)d$

$\Rightarrow 10 = 34 + (n-1)(-2)$

$\Rightarrow -26 = -2n$

$\Rightarrow n = 13$

Now, we know that

$S = \frac{n}{2}\left \{ a+a_n \right \}$

$\Rightarrow S = \frac{13}{2}\left \{ 44\right \}$

$\Rightarrow S =13\times 22 = 286$

Therefore, the sum of AP $\small 34+32+30+...+10$ is 286

Q2 (iii) Find the sums given below: $\small -5+(-8)+(-11)+...+(-230)$

Answer:

Given series $\small -5+(-8)+(-11)+...+(-230)$

First we need to find the number of terms

Here, $a = -5 \ and \ a_n = -230$ and $d = a_2-a_1=-8-(-5)= -3$

Let suppose there are n terms in the AP

Now, we know that

$a_n = a+(n-1)d$

$\Rightarrow -230 = -5 + (n-1)(-3)$

$\Rightarrow -228 = -3n$

$\Rightarrow n = 76$

Now, we know that

$S = \frac{n}{2}\left \{ a+a_n \right \}$

$\Rightarrow S = \frac{76}{2}\left \{ (-5-230 )\right \}$

$\Rightarrow S = 38\left \{ -235\right \}$

$\Rightarrow S = -8930$

Therefore, the sum of AP $\small -5+(-8)+(-11)+...+(-230)$ is -8930

Q3 (i) In an AP: given $\small a=5$ , $\small d=3$ , $\small a_n=50$ , find $\small n$ and $\small S_n$ .

Answer:

Given $a = 5, d = 3 \ and \ a_n = 50$

Let suppose there are n terms in the AP

Now, we know that

$a_n = a+(n-1)d$

$\Rightarrow 50 = 5 + (n-1)3$

$\Rightarrow 48 = 3n$

$\Rightarrow n = 16$

Now, we know that

$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S = \frac{16}{2}\left \{ 2\times(5) +(16-1)(3)\right \}$

$\Rightarrow S = 8\left \{ 10+45\right \}$

$\Rightarrow S = 8\left \{ 55\right \}$

$\Rightarrow S =440$

Therefore, the sum of the given AP is 440

Q3 (ii) In an AP: given $\small a=7$ , $\small a_1_3=35$ , find $\small d$ and $\small S_1_3$ .

Answer:

Given $a = 7 \ and \ a_{13} = 35$

$a_{13}= a+12d = 35$

$= 12d = 35-7 = 28$

$d = \frac{28}{12}= \frac{7}{3}$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{13} = \frac{13}{2}\left \{ 2\times(7) +(13-1)(\frac{7}{3})\right \}$

$\Rightarrow S_{13} = \frac{13}{2}\left \{14 +28\right \}$

$\Rightarrow S_{13} = \frac{13}{2}\left \{42\right \}$

$\Rightarrow S_{13} = 13 \times 21 = 273$

Therefore, the sum of given AP is 273

Q3 (iii) In an AP: given $\small a_1_2=37,d=3,$ find $\small a$ and $\small S_1_2$ .

Answer:

Given $d = 3 \ and \ a_{12} = 37$

$a_{12}= a+11d = 37$

$= a= 37-11\times 3 = 37-33=4$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{12} = \frac{12}{2}\left \{ 2\times(4) +(12-1)3\right \}$

$\Rightarrow S_{12} = 6\left \{ 8+33\right \}$

$\Rightarrow S_{12} = 6\left \{41\right \}$

$\Rightarrow S_{12} =246$

Therefore, the sum of given AP is 246

Q3 (iv) In an AP: given $\small a_3=15, S_1_0=125,$ find $\small d$ and $\small S_1_0$

Answer:

Given $\small a_3=15, S_1_0=125$

$a_{3}= a+2d = 15 \ \ \ \ \ \ \ \ -(i)$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{10} = \frac{10}{2}\left \{ 2\times(a) +(10-1)d\right \}$

$\Rightarrow 125 = 5\left \{ 2a+9d\right \}$

$\Rightarrow 2a+9d = 25 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$

On solving equation (i) and (ii) we will get

$a= 17 \ and \ d = -1$

Now, $a_{10} = a+ 9d = 17 + 9(-1)= 17-9 = 8$

Therefore, the value of d and 10th terms is -1 and 8 respectively

Q3 (v) In an AP: given $\small d=5, S_9=75$ , find $\small a$ and $\small a_9$ .

Answer:

Given $\small d=5, S_9=75$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{9} = \frac{9}{2}\left \{ 2\times(a) +(9-1)5\right \}$

$\Rightarrow 75= \frac{9}{2}\left \{ 2a +40\right \}$

$\Rightarrow 150= 18a+360$

$\Rightarrow a = -\frac{210}{18}=-\frac{35}{3}$

Now, $a_{9} = a+ 8d = -\frac{35}{3} + 8(5)= -\frac{35}{3}+40 = \frac{-35+120}{3}= \frac{85}{3}$

Q3 (vi) In an AP: given $\small a=2,d=8,S_n=90,$ find $\small n$ and $\small a_n$ .

Answer:

Given $\small a=2,d=8,S_n=90,$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow 90 = \frac{n}{2}\left \{ 2\times(2) +(n-1)8\right \}$

$\Rightarrow 180 = n\left \{ 4+8n-8\right \}$

$\Rightarrow 8n^2-4n-180=0$

$\Rightarrow 4(2n^2-n-45)=0$

$\Rightarrow 2n^2-n-45=0$

$\Rightarrow 2n^2-10n+9n-45=0$

$\Rightarrow (n-5)(2n+9)=0$

$\Rightarrow n = 5 \ \ and \ \ n = - \frac{9}{2}$

We know that 'n' can not be negative so the only the value of n is 5

Now,

$a_{5} = a+ 4d = 2+4\times 8 = 2+32 = 34$

Therefore, value of n and nth term is 5 and 34 respectively

Q3 (vii) In an AP: given $\small a=8,a_n=62,S_n=210,$ find $\small n$ and $\small d$.

Answer:

Given $\small a=8,a_n=62,S_n=210,$

Now, we know that

$a_n = a+(n-1)d$

$62 = 8+(n-1)d$

$(n-1)d= 54 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow 210 = \frac{n}{2}\left \{ 2\times(8) +(n-1)d\right \}$

$\Rightarrow 420 = n\left \{ 16+54 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$

$\Rightarrow 420 = n\left \{ 70 \right \}$

$\Rightarrow n = 6$

Now, put this value in (i) we will get

$d = \frac{54}{5}$

Therefore, value of n and d are $6 \ and \ \frac{54}{5}$ respectively

Q3 (viii) In an AP: given $\small a_n=4,d=2,S_n=-14,$ find $\small n$ and $\small a$ .

Answer:

Given $\small a_n=4,d=2,S_n=-14,$

Now, we know that

$a_n = a+(n-1)d$

$4 = a+(n-1)2$

$a+2n = 6\Rightarrow a = 6-2n \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow -14 = \frac{n}{2}\left \{ 2\times(a) +(n-1)2\right \}$

$\Rightarrow -28 = n\left \{ 2(6-2n)+2n-2 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$

$\Rightarrow -28 = n\left \{ 10-2n \right \}$

$\Rightarrow 2n^2-10n-28=0$

$\Rightarrow 2(n^2-5n-14)=0$

$\Rightarrow n^2-7n+2n-14=0$

$\Rightarrow(n+2)(n-7)=0$

$\Rightarrow n = -2 \ \ and \ \ n = 7$

Value of n cannot be negative so the only the value of n is 7

Now, put this value in (i) we will get

a = -8

Therefore, the value of n and a are 7 and -8 respectively

Q3 (ix) In an AP: given $\small a=3,n=8,S=192,$ find $\small d$ .

Answer:

Given $\small a=3,n=8,S=192,$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow 192 = \frac{8}{2}\left \{ 2\times(3) +(8-1)d\right \}$

$\Rightarrow 192=4\left \{6 +7d\right \}$

$\Rightarrow 7d = 48-6$

$\Rightarrow d = \frac{42}{7} = 6$

Therefore, the value of d is 6

Q3 (x) In an AP: given $\small l=28,S=144 \ and \ n = 9$ and there are total $\small 9$ terms. Find $\small a$ .

Answer:

Given $\small l=28,S=144 \ and \ n = 9$

Now, we know that

$l = a_n = a+(n-1)d$

$28 = a_n = a+(n-1)d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow 144 = \frac{9}{2}\left \{ a + a +(n-1)d\right \}$

$\Rightarrow 288 =9\left \{ a+ 28\right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(using \ (i))$

$\Rightarrow a+28= 32$

$\Rightarrow a=4$

Therefore, the value of a is 4

Q4 How many terms of the AP: $\small 9,17,25,...$ must be taken to give a sum of $\small 636$ ?

Answer:

Given series $\small 9,17,25,...$

Here, $a =9 \ and \ d = 8$

And $S_n = 636$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

After putting values we get:

$\Rightarrow 636 = \frac{n}{2}\left \{ 18+(n-1)8 \right \}$

$\Rightarrow 1272 = n\left \{ 10+8n \right \}$

$\Rightarrow 8n^2+10n-1272=0$

$\Rightarrow 2(4n^2+5n-636)=0$

$\Rightarrow 4n^2+53n-48n-636=0$

$\Rightarrow (n-12)(4n+53)=0$

$\Rightarrow n = 12 \ \ and \ \ n = - \frac{53}{4}$

The value of n can not be negative, so the only value of n is 12

Therefore, the sum of 12 terms of AP $\ small9,17,25,...$ must be taken to give a sum of $\small 636$.

Q5 The first term of an AP is $\small 5$ , the last term is $\small 45$ and the sum is $\small 400$ . Find the number of terms and the common difference.

Answer:

Given $\small a=5,a_n=45,S_n=400,$

Now, we know that

$a_n = a+(n-1)d$

$45 = 5+(n-1)d$

$(n-1)d= 40 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow 400 = \frac{n}{2}\left \{ 2\times(5) +(n-1)d\right \}$

$\Rightarrow 800 = n\left \{ 10+40 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$

$\Rightarrow 800 = n\left \{ 50 \right \}$

$\Rightarrow n = 16$

Now, put this value in (i), we will get

$d = \frac{40}{15}= \frac{8}{3}$

Therefore, value of n and d are $16 \ and \ \frac{8}{3}$ respectively

Q6 The first and the last terms of an AP are $\small 17$ and $\small 350$ respectively. If the common difference is $\small 9$ , how many terms are there and what is their sum?

Answer:

Given $\small a=17,l=350,d=9,$

Now, we know that

$a_n = a+(n-1)d$

$350 = 17+(n-1)9$

$(n-1)9 = 333$

$(n-1)=37$

$n = 38$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{38}= \frac{38}{2}\left \{ 2\times(17) +(38-1)9\right \}$

$\Rightarrow S_{38}= 19\left \{ 34 +333\right \}$

$\Rightarrow S_{38}= 19\left \{367\right \}$

$\Rightarrow S_{38}= 6973$

Therefore, there are 38 terms and their sum is 6973.

Q7 Find the sum of first $\small 22$ terms of an AP in which $\small d=7$ and $\small 22$ nd term is $\small 149$ .

Answer:

Given $\small a_{22}=149,d=7,n = 22$

Now, we know that

$a_{22} = a+21d$

$149 = a+21\times 7$

$a = 149 - 147 = 2$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{22}= \frac{22}{2}\left \{ 2\times(2) +(22-1)7\right \}$

$\Rightarrow S_{22}= 11\left \{ 4 +147\right \}$

$\Rightarrow S_{22}= 11\left \{ 151\right \}$

$\Rightarrow S_{22}= 1661$

Therefore, there are 22 terms and their sum is 1661.

Q8 Find the sum of first $\small 51$ terms of an AP whose second and third terms are $\small 14$ and $\small 18$ respectively.

Answer:

Given $\small a_{2}=14,a_3=18,n = 51$ and $d= a_3-a_2= 18-14=4$

Now,

$a_2 = a+d$

$a= 14-4 = 10$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{51}= \frac{51}{2}\left \{ 2\times(10) +(51-1)4\right \}$

$\Rightarrow S_{51}= \frac{51}{2}\left \{ 20 +200\right \}$

$\Rightarrow S_{51}= \frac{51}{2}\left \{ 220\right \}$

$\Rightarrow S_{51}= 51 \times 110$

$\Rightarrow S_{51}=5304$

Therefore, there are 51 terms and their sum is 5610.

Q9 If the sum of first $\small 7$ terms of an AP is $\small 49$ and that of $\small 17$ terms is $\small 289$ , find the sum of first $\small n$ terms.

Answer:

Given $S_7 = 49 \ and \ S_{17}= 289$

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

After putting values we get:

$\Rightarrow S_{7}= \frac{7}{2}\left \{ 2\times(a) +(7-1)d\right \}$

$\Rightarrow 98= 7\left \{ 2a +6d\right \}$

$\Rightarrow a +3d = 7 \ \ \ \ \ \ \ -(i)$

Similarly,

$\Rightarrow S_{17}= \frac{17}{2}\left \{ 2\times(a) +(17-1)d\right \}$

$\Rightarrow 578= 17\left \{ 2a +16d\right \}$

$\Rightarrow a +8d = 17 \ \ \ \ \ \ \ -(ii)$

On solving equations (i) and (ii), we will get

a = 1 and d = 2

Now, the sum of the first n terms is

$S_n = \frac{n}{2}\left \{ 2\times 1 +(n-1)2 \right \}$

$S_n = \frac{n}{2}\left \{ 2 +2n-2 \right \}$

$S_n = n^2$

Therefore, the sum of n terms is $n^2$.

Q10 (i) Show that $\small a_1,a_2,...,a_n,...$ form an AP where an is defined as below: $\small a_n=3+4n$ Also find the sum of the first $\small 15$ terms.

Answer:

Given $\small a_n=3+4n$

We will check the values of $a_n$ for different values of n

$a_1 = 3+4(1) =3+4= 7$

$a_2 = 3+4(2) =3+8= 11$

$a_3 = 3+4(3) =3+12= 15$ and so on.

From the above, we can see that this is an AP with the first term(a) equal to 7 and a common difference (d) equal to 4

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times(7) +(15-1)4\right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 14 +56\right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 70\right \}$

$\Rightarrow S_{15}= 15 \times 35$

$\Rightarrow S_{15}= 525$

Therefore, the sum of 15 terms is 525.

Q10 (ii) Show that $\small a_1,a _2,...,a_n,...$ form an AP where an is defined as below: $\small a_n=9-5n$ . Also find the sum of the first $\ small15$ terms in each case .

Answer:

Given $\small a_n=9-5n$

We will check the values of $a_n$ for different values of n

$a_1 = 9-5(1) =9-5= 4$

$a_2 = 9-5(2) =9-10= -1$

$a_3 = 9-5(3) =9-15= -6$ and so on.

From the above, we can see that this is an AP with the first term (a) equal to 4 and common difference (d) equal to -5

Now, we know that

$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times(4) +(15-1)(-5)\right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 8 -70\right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ -62\right \}$

$\Rightarrow S_{15}= 15 \times (-31)$

$\Rightarrow S_{15}= -465$

Therefore, the sum of 15 terms is -465.

Q11 If the sum of the first $\small n$ terms of an AP is $\small 4n-n^2$ , what is the first term (that is $\small S_1$ )? What is the sum of first two terms? What is the second term? Similarly, find the $\small 3$ rd, the $\small 10$ th and the $\small n$ th terms

Answer:

Given that the sum of the first $\small n$ terms of an AP is $\small 4n-n^2$

Now,

$\Rightarrow S_n = 4n-n^2$

Now, first term is

$\Rightarrow S_1 = 4(1)-1^2=4-1=3$

Therefore, first term is 3
Similarly,

$\Rightarrow S_2 = 4(2)-2^2=8-4=4$

Therefore, sum of first two terms is 4

Now, we know that

$\Rightarrow S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_2 = \frac{2}{2}\left \{ 2\times 3+(2-1)d \right \}$

$\Rightarrow 4 = \left \{6+d \right \}$

$\Rightarrow d = -2$

Now,

$a_2= a+d = 3+(-2 )= 1$

Similarly,

$a_3= a+2d = 3+2(-2 )= 3-4=-1$

$a_{10}= a+9d = 3+9(-2 )= 3-18=-15$

$a_{n}= a+(n-1)d = 3+(n-1)(-2 )= 5-2n$

Q12 Find the sum of the first $\small 40$ positive integers divisible by $\small 6$ .

Answer:

Positive integers divisible by 6 are 6,12,18,...

Thus, this is an AP with

$here, \ a = 6 \ and \ d = 6$

Now, we know that

$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{40}= \frac{40}{2}\left \{ 2\times 6+(40-1)6 \right \}$

$\Rightarrow S_{40}= 20\left \{12+234 \right \}$

$\Rightarrow S_{40}= 20\left \{246 \right \}$

$\Rightarrow S_{40}= 4920$

Therefore, sum of the first $\small 40$ positive integers divisible by $\small 6$ is 4920.

Q13 Find the sum of the first $\small 15$ multiples of $\small 8$ .

Answer:

The first 15 multiples of 8 are 8,16,24,...

Therefore, this is an AP with

$here, \ a = 8 \ and \ d = 8$

Now, we know that

$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times 8+(15-1)8 \right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 16+112 \right \}$

$\Rightarrow S_{15}= \frac{15}{2}\left \{ 128 \right \}$

$\Rightarrow S_{15}= 15 \times 64 = 960$

Therefore, the sum of the first 15 multiples of 8 is 960.

Q14 Find the sum of the odd numbers between $\small 0$ and $\small 50$ .

Answer:

The odd numbers between 0 and 50 are 1,3,5,...49

This is an AP with

$here, \ a = 1 \ and \ d = 2$

There are a total of 25 odd numbers between 0 and 50

Now, we know that

$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\Rightarrow S_{25}= \frac{25}{2}\left \{ 2\times 1+(25-1)2 \right \}$

$\Rightarrow S_{25}= \frac{25}{2}\left \{ 2+48 \right \}$

$\Rightarrow S_{25}= \frac{25}{2}\times 50$

$\Rightarrow S_{25}= 25 \times 25 = 625$

Therefore, sum of the odd numbers between $\small 0$ and $\small 50$ 625

Q15 A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs $\small 200$ for the first day, Rs $\small 250$ for the second day, Rs $\small 300$ for the third day, etc., the penalty for each succeeding day being Rs $\small 50$ more than for the preceding day. How much money the contractor has to pay a penalty, if he has delayed the work by $\small 30$ days?

Answer:

Given: Penalty for delay of completion beyond a certain date is Rs $\small 200$ for the first day, Rs $\small 250$ for the second day, Rs $\small 300$ for the third day, and a penalty for each succeeding day being Rs $\small 50$ more than for the preceding day

We can see that

200,250,300,..... is an AP with

$a = 200 \ and \ d = 50$

Now, the penalty for 30 days is given by the expression

$S_{30}= \frac{30}{2}\left \{ 2\times 200+(30-1)50 \right \}$

$S_{30}= 15\left ( 400+1450 \right )$

$S_{30}= 15 \times 1850$

$S_{30}= 27750$

Therefore, the penalty for 30 days is 27750

Q16 A sum of Rs $\small 700$ is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs $\small 20$ less than its preceding prize, find the value of each of the prizes.

Answer:

Given: each price is decreased by 20 rupees,

Therefore, d = -20 and there are total 7 prizes so n = 7 and sum of prize money is Rs 700 so $S_7 = 700$

Let a be the prize money given to the 1st student

Then, $S_7 = \frac{7}{2}\left \{ 2a+(7-1)(-20) \right \}$

$700 = \frac{7}{2}\left \{ 2a-120 \right \}$

$2a - 120 = 200$

$a = \frac{320}{2}= 160$

Therefore, the prize given to the first student is Rs 160

Now, Let $a_2,a_2,...,a_7$ is the prize money given to the next 6 students

Thus, $a_2 = a+d = 160+(-20)=160-20=140$

$a_3 = a+2d = 160+2(-20)=160-40=120$

$a_4 = a+3d = 160+3(-20)=160-60=100$

$a_5 = a+4d = 160+4(-20)=160-80=80$

$a_6 = a+5d = 160+5(-20)=160-100=60$

$a_7 = a+6d = 160+6(-20)=160-120=40$

Therefore, the prize money given to 1 to 7 students is 160, 140, 120, 100, 80, 60, 40.

Q17 In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I???? will plant $\small 1$ tree, a section of Class II will plant $\small 2$ trees and so on till Class XII. There are three sections in each class. How many trees will be planted by the students?

Answer:

First, there are 12 classes,s and each class has 3 sections

Since each section of class 1 will plant 1 tree, so 3 trees will be planted by 3 sections of class 1. Thus every class will plant 3 times the number of their class

Similarly,

No. of trees planted by 3 sections of class 1 = 3

Number of trees planted by 3 sections of class 2 = 6

No. of trees planted by 3 sections of class 3 = 9

Number of trees planted by 3 sections of class 4 = 12

Its clearly an AP with first term (a) = 3 and common difference (d) = 3 and total number of classes (n) = 12

Now, the number of trees planted by 12 classes is given by

$S_{12}= \frac{12}{2}\left \{ 2\times 3+(12-1)\times 3 \right \}$

$S_{12}= 6\left ( 6+33 \right )$

$S_{12}= 6 \times 39 = 234$

Therefore, the number of trees planted by 12 classes is 234.

Q18 A spiral is made up of successive semicircles, with centres alternately at $\small A$ and $\small B$ ??????, starting with centre at $\small A$ , of radii $\small 0.5\hspace {1mm}cm,1.0\hspace {1mm}cm,1.5\hspace {1mm}cm,2.0\hspace {1mm}cm,...$ as shown in Fig. $\small 5.4$ . What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take $\pi =\frac{22}{7}$ )

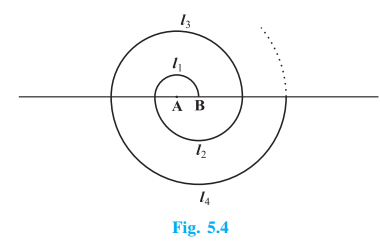
[ Hint : Length of successive semicircles is $\small l_1,l_2,l_3,l_4,...$ with centres at $\small A,B,A,B,...,$ respectively.]

Answer:

From the above-given figure

Circumference of 1st semicircle $l_1 = \pi r_1 = 0.5\pi$

Similarly,

Circumference of 2nd semicircle $l_2 = \pi r_2 = \pi$

Circumference of 3rd semicircle $l_3 = \pi r_3 = 1.5\pi$

It is clear that this is an AP with $a = 0.5\pi \ and \ d = 0.5\pi$

Now, the sum of the lengths of 13 such semicircles is given by

$S_{13} = \frac{13}{2}\left \{ 2\times 0.5\pi + (13-1)0.5\pi\right \}$

$S_{13} = \frac{13}{2}\left ( \pi+6\pi \right )$

$S_{13} = \frac{13}{2}\times 7\pi$

$S_{13} = \frac{91\pi}{2} = \frac{91}{2}\times \frac{22}{7}=143$

Therefore, sum of length of 13 such semicircles is 143 cm

Q19 $\small 200$ logs are stacked in the following manner: $\small 20$ logs in the bottom row, $\small 19$ in the next row, $\small 18$ in the row next to it and so on (see Fig. $\small 5.5$ ). In how many rows are the $\small 200$ logs placed and how many logs are in the top row?

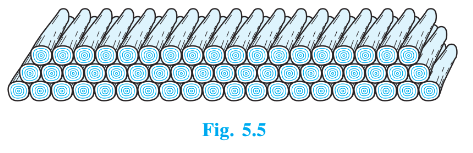
Answer:

As the rows are going up, the number of logs is decreasing,

We can clearly see that 20, 19, 18, ..., is an AP and here $a = 20 \ and \ d = -1$

Let's suppose 200 logs are arranged in 'n' rows,

Then,

$S_n = \frac{n}{2}\left \{ 2\times 20 +(n-1)(-1) \right \}$

$200 = \frac{n}{2}\left \{ 41-n \right \}$

$\Rightarrow n^2-41n +400 = 0$

$\Rightarrow n^2-16n-25n +400 = 0$

$\Rightarrow (n-16)(n-25) = 0$

$\Rightarrow n = 16 \ \ and \ \ n = 25$

Now, case (i) n = 25

$a_{25} =a+24d = 20+24\times (-1)= 20-24=-4$

But number of rows can not be in negative numbers

Therefore, we will reject the value n = 25

Case (ii) n = 16

$a_{16} =a+15d = 20+15\times (-1)= 20-15=5$

Therefore, the number of rows in which 200 logs are arranged is equal to 5.

Q20 In a potato race, a bucket is placed at the starting point, which is $\small 5$ m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Fig. $\small 5.6$ ).

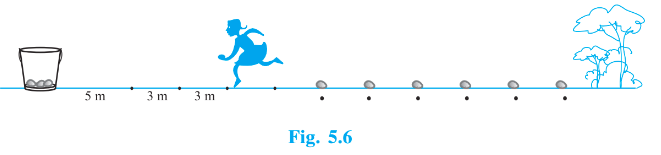
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?

[ Hint: To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is $\small 2\times5+2\times (5+3)$ ]

Answer:

Distance travelled by the competitor in picking and dropping 1st potato $= 2 \times 5 = 10 \ m$

Distance travelled by the competitor in picking and dropping 2nd potato $= 2 \times (5+3) =2\times 8 = 16 \ m$

Distance travelled by the competitor in picking and dropping 3rd potato $= 2 \times (5+3+3) =2\times 11 = 22 \ m$ and so on

We can see that it is an AP with first term (a) = 10 and common difference (d) = 6

There are 10 potatoes in the line

Therefore, the total distance travelled by the competitor in picking and dropping potatoes is

$S_{10}= \frac{10}{2}\left \{ 2\times 10+(10-1)6 \right \}$

$S_{10}= 5\left ( 20+54 \right )$

$S_{10}= 5\times 74 = 370$

Therefore, the total distance travelled by the competitor in picking and dropping potatoes is 370 m