NCERT Solutions for Class 10 Maths Chapter 5 Exercise 5.4 - Arithmetic Progressions

Q1. Which term of the AP: is its first negative term $\small 121,117,113,...,$? [Hint : Find $n$ for $a_n<0$]

Answer:

Given AP is

$\small 121,117,113,...,$

Here $a = 121 \ and \ d = -4$

Let's suppose the nth term of the AP is the first negative term

Then,

$a_n = a+ (n-1)d$

If the nth term is negative, then $a_n < 0$

$\Rightarrow 121+(n-1)(-4) < 0$

$\Rightarrow 125<4n$

$\Rightarrow n > \frac{125}{4}=31.25$

Therefore, the first negative term must be the 32nd term

Q2. The sum of the third and the seventh terms of an AP is $\small 6$ and their product is $\small 8$ . Find the sum of first sixteen terms of the AP.

Answer:

It is given that the sum of the third and seventh terms of an AP is and their product is $\small 8$

$a_3= a+ 2d$

$a_7= a+ 6d$

Now,

$a_3+a_7= a+ 2d+a+6d= 6$

$\Rightarrow 2a+8d = 6$

$\Rightarrow a+4d = 3 \Rightarrow a = 3-4d \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

And

$a_3.a_7 = (a+2d).(a+6d)=a^2+8ad +12d^2 = 8 \ \ \ \ \ \ \ -(ii)$

Putting the value from equation (i) in equation (ii), we will get

$\Rightarrow (3-4d)^2+8(3-4d)d+12d^2= 8$

$\Rightarrow 9+16d^2-24d+24d-32d^2+12d^2=8$

$\Rightarrow 4d^2 = 1$

$\Rightarrow d = \pm \frac{1}{2}$

Now,

Case (i) $d = \frac{1}{2}$

$a= 3 - 4 \times \frac{1}{2} = 1$

Then,

$S_{16}=\frac{16}{2}\left \{ 2\times 1+(16-1)\frac{1}{2} \right \}$

$S_{16}=76$

Case (ii) $d = -\frac{1}{2}$

$a= 3 - 4 \times \left ( -\frac{1}{2} \right ) = 5$

Then,

$S_{16}=\frac{16}{2}\left \{ 2\times 1+(16-1)\left ( -\frac{1}{2} \right ) \right \}$

$S_{16}=20$

Q3. A ladder has rungs $\small 25$ cm apart. (see Fig. $\small 5.7$ ). The rungs decrease uniformly in length from $\small 45$ cm at the bottom to $\small 25$ cm at the top. If the top and the bottom rungs are $\small 2\frac{1}{2}$ m apart, what is the length of the wood required for the rungs? [Hint:Number of rungs = $\frac{250}{25}+1$]

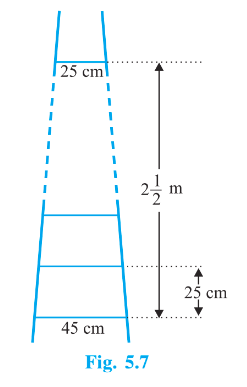
Answer:

It is given that

The total distance between the top and bottom rung $= 2\frac{1}{2}\ m = 250cm$

Distance between any two rungs = 25 cm

Total number of rungs = $\frac{250}{25}+1= 11$

And it is also given that the bottom-most rung is of 45 cm length and the top-most is of 25 cm length. As it is given that the length of rungs

decreases uniformly, it will form an AP with $a = 25, a_{11} = 45 \ and \ n = 11$

Now, we know that

$a_{11}= a+ 10d$

$\Rightarrow 45=25+10d$

$\Rightarrow d = 2$

Now, the total length of the wood required for the rungs is equal to

$S_{11} = \frac{11}{2}\left \{ 2\times 25+(11-1)2 \right \}$

$S_{11} = \frac{11}{2}\left \{ 50+20 \right \}$

$S_{11} = \frac{11}{2}\times 70$

$S_{11} =385 \ cm$

Therefore, the total length of the wood required for the rungs is equal to 385 cm

Q4 The houses of a row are numbered consecutively from $\ small1$ to $\ small49$. Show that there is a value of $\small x$ such that the sum of the numbers of the houses preceding the house numbered $\small x$ is equal to the sum of the numbers of the houses following it. Find the value of $\ small x$.

Answer:

It is given that the sum of the numbers of the houses preceding the house numbered $\small x$ is equal to the sum of the numbers of the

houses following it

And 1,2,3,.....,49 form an AP with a = 1 and d = 1

Now, we know that

$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$

Suppose there exists an n term such that ( n < 49)

Now, according to the given conditions

The sum of the first n - 1 terms of AP = The sum of the terms following the nth term

Sum of the first n - 1 terms of AP = Sum of the whole AP - Sum of the first m terms of AP

i.e.

$S_{n-1}=S_{49}-S_n$

$\frac{n-1}{2}\left \{ 2a+((n-1)-1)d \right \}=\frac{49}{2}\left \{ 2a+(49-1)d \right \}-\frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\frac{n-1}{2}\left \{ 2+(n-2) \right \}=\frac{49}{2}\left \{ 2+48 \right \}-\frac{n}{2}\left \{ 2+(n-1) \right \}$

$\frac{n-1}{2}\left \{ n\right \}=\frac{49}{2}\left \{ 50 \right \}-\frac{n}{2}\left \{ n+1 \right \}$

$\frac{n^2}{2}-\frac{n}{2}=1225-\frac{n^2}{2}-\frac{n}{2}$

$n^2 = 1225$

$n = \pm 35$

Given House numbers are not negative,e so we reject n = -35

Therefore, the sum of no of houses preceding house no 35 is equal to the sum of no of houses following house number 35.

Q5. A small terrace at a football ground comprises of $\small 15$ steps each of which is $\small 50$ m long and built of solid concrete. Each step has a rise of $\small \frac{1}{4}\: m$ and a tread of $\small \frac{1}{2}\: m$ . (see Fig. $\small 5.8$ ). Calculate the total volume of concrete required to build the terrace.
[ Hint: Volume of concrete required to build the first step $\small =\frac{1}{4}\times \frac{1}{2}\times 50\: m^3$ ]

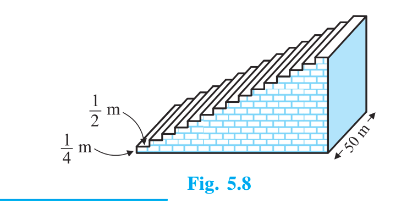
Answer:

It is given that

football ground comprises of $\small 15$ steps each of which is $\small 50$ m long and Each step has a rise of $\small \frac{1}{4}\: m$

and a tread of $\small \frac{1}{2}\: m$

Now,

The volume required to make the first step = $\frac{1}{4}\times \frac{1}{2}\times 50 = 6.25 \ m^3$

Similarly,

The volume required to make 2nd step = $\left ( \frac{1}{4}+\frac{1}{4}\right )\times \frac{1}{2}\times 50=\frac{1}{2}\times \frac{1}{2}\times 50 = 12.5 \ m^3$

And

The volume required to make 3rd step = $\left ( \frac{1}{4}+\frac{1}{4}+\frac{1}{4}\right )\times \frac{1}{2}\times 50=\frac{3}{4}\times \frac{1}{2}\times 50 = 18.75 \ m^3$

And so on

We can see that this is an AP with $a= 6.25 \ and \ d = 6.25$

Now, the total volume of concrete required to build the terrace of 15 such steps is

$S_{15} =\frac{15}{2}\left \{ 2 \times 6.25 +(15-1)6.25 \right \}$

$S_{15} =\frac{15}{2}\left \{ 12.5 +87.5\right \}$

$S_{15} =\frac{15}{2}\times 100$

$S_{15} =15\times 50 = 750$

Therefore, the total volume of concrete required to build the terrace of 15 such steps is $750 \ m^3$