• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 2.4 Class 10 Maths Chapter 2 - Polynomials

NCERT Solutions for Exercise 2.4 Class 10 Maths Chapter 2 - Polynomials

Edited By Ramraj Saini | Updated on Nov 08, 2023 06:25 PM IST | #CBSE Class 10th
Upcoming Event
CBSE Class 10th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.4 Polynomials

NCERT Solutions for class 10 maths ex 2.4 Polynomials is discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. This class 10 ex 2.4 deals with polynomial and its types, algebraic expressions, degree of a polynomial expression, graphical representation of the polynomial equations, factorization, relationship between zeroes and coefficient of a polynomial.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.4 Polynomials
  2. Download PDF of NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.4 Polynomials
  3. Access Exercise 2.4 Class 10 Maths Answers
  4. More About NCERT Solutions for Class 10 Maths Exercise 2.4:
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 2.4
  6. NCERT Solutions of Class 10 Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 2.4 Class 10 Maths Chapter 2 - Polynomials
NCERT Solutions for Exercise 2.4 Class 10 Maths Chapter 2 - Polynomials

Mathematically, the number of terms and the degree of the polynomial, polynomial can be classified into many types. Based on the number of terms, polynomials are classified as Monomial, Binomial and Trinomial. Also based on Degree, polynomials are classified as Linear Polynomial, Quadratic polynomial and Cubic Polynomial. Along with the Class 10 Maths chapter, 2 exercise 2.4 the following exercises are also present. Students should practice all problems discussed in these exercises to command the concepts.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Download PDF of NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.4 Polynomials

Download PDF

Access Exercise 2.4 Class 10 Maths Answers

Polynomials Class 10 Maths Chapter 2 Excercise: 2.4

Q1 (1) Verify that the numbers given alongside the cubic polynomials below are their zeroes.
Also verify the relationship between the zeroes and the coefficients in each case:
2x^3 + x^2 - 5x +2 ; \frac{1}{2} , 1 , -2

Answer:

p(x) = 2x 3 + x 2 -5x + 2

\\p(\frac{1}{2})=2\times \left ( \frac{1}{2} \right )^{3}+\left ( \frac{1}{2} \right )^{2}-5\times \frac{1}{2}+2\\ p(\frac{1}{2})=\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+2\\ p(\frac{1}{2})=0

p(1) = 2 x 1 3 + 1 2 - 5 x 1 + 2

p(1) =2 + 1 - 5 + 2

p(1) = 0

p(-2) = 2 x (-2) 3 + (-2) 2 - 5 x (-2) +2

p(-2) = -16 + 4 + 10 + 2

p(-2) = 0

Therefore the numbers given alongside the polynomial are its zeroes

Verification of relationship between the zeroes and the coefficients

Comparing the given polynomial with ax 3 + bx 2 + cx + d, we have

a = 2, b = 1, c = -5, d = 2

The roots are \alpha ,\beta \ and\ \gamma

\\\alpha=\frac{1}{2}\\ \beta =1\\ \gamma =-2

\\\alpha+\beta +\gamma \\ =\frac{1}{2}+1+(-2)\\ =-\frac{1}{2}\\ =-\frac{b}{a}

Verified

\\\alpha\beta +\beta \gamma +\gamma \alpha \\ =\frac{1}{2}\times 1+1\times (-2)+(-2)\times \frac{1}{2}\\ =\frac{-5}{2}\\ =\frac{c}{a}

Verified

\\\alpha\beta\gamma \\=\frac{1}{2}\times 1\times -2\\ =-1 \\=-\frac{2}{2}\\ =-\frac{d}{a}

Verified

Q1 (2) Verify that the numbers given alongside the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:

x ^ 3- 4x ^ 2 + 5x - 2 ; 2,1,1

Answer:

p(x) = x 3 - 4x 2 + 5x - 2

p(2) = 2 3 - 4 x 2 2 + 5 x 2 - 2

p(2) = 8 - 16 + 10 - 2

p(-2) = 0

p(1) = 1 3 - 4 x 1 2 + 5 x 1 - 2

p(1) = 1 - 4 + 5 - 2

p(1) = 0

Therefore the numbers given alongside the polynomial are its zeroes

Verification of relationship between the zeroes and the coefficients

Comparing the given polynomial with ax 3 + bx 2 + cx + d, we have

a = 1, b = -4, c = 5, d = -2

The roots are \alpha ,\beta \ and\ \gamma

\\\alpha=2\\ \beta =1\\ \gamma =1

\\\alpha+\beta +\gamma \\ =2+1+1\\ =4\\ =-\frac{-4}{1}\\=-\frac{b}{a}

Verified

\\\alpha\beta +\beta \gamma +\gamma \alpha \\ =2\times 1+1\times 1+1\times 2\\ =5\\ =\frac{5}{1}\\ =\frac{c}{a}

Verified

\\\alpha\beta\gamma \\=2\times 1\times 1\\=2 \\=-\frac{-2}{1}\\=-\frac{d}{a}

Verified

Q2 Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.

Answer: Let the roots of the polynomial be \alpha ,\beta \ and\ \gamma

\\\alpha +\beta +\gamma =2\\ \alpha \beta +\beta \gamma +\gamma \alpha =-7\\ \alpha \beta \gamma =-14

\\x^{3}-(\alpha +\beta +\gamma )x^{2}+(\alpha \beta +\beta \gamma +\gamma \alpha)x-\alpha \beta \gamma =0\\ x^{3}-2x^{2}-7x+14=0

Hence the required cubic polynomial is x 3 - 2x 2 - 7x + 14 = 0

Q3 If the zeroes of the polynomial x^3 - 3 x^2+ x +1 are a – b, a, a + b, find a and b.

Answer:

x^3 - 3 x^2+ x +1

The roots of the above polynomial are a, a - b and a + b

Sum of the roots of the given plynomial = 3

a + (a - b) + (a + b) = 3

3a = 3

a = 1

The roots are therefore 1, 1 - b and 1 + b

Product of the roots of the given polynomial = -1

1 x (1 - b) x (1 + b) = - 1

1 - b 2 = -1

b 2 - 2 = 0

b=\pm \sqrt{2}

Therefore a = 1 and b=\pm \sqrt{2} .

Q4 If two zeroes of the polynomial x^4 - 6x ^3 - 26 x^2 + 138 x - 35 x^4 - 6x ^3 - 26 x^2 + 138 x - 35 are 2 \pm \sqrt 3 , find other zeroes .

Answer: Given the two zeroes are

2+\sqrt{3}\ and\ 2-\sqrt{3}

therefore the factors are

[x-(2+\sqrt{3})]\ and[x-(\ 2-\sqrt{3})]

We have to find the remaining two factors. To find the remaining two factors we have to divide the polynomial with the product of the above factors

[x-(2+\sqrt{3})]\[x-(\ 2-\sqrt{3})]=x^2-(2+\sqrt{3})x-(\ 2-\sqrt{3})x+(\ 2+\sqrt{3})(\ 2-\sqrt{3})\\=x^2-2x-\sqrt{3}x-2x+\sqrt{3}x+1\\=x^2-4x+1

Now carrying out the polynomial division

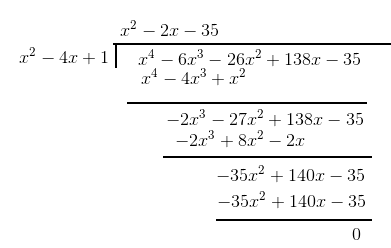
1635919283320

Now we get x^2-2x -35 \ is \ also \ a\ factor

\\x^2-2x -35 =x^2-7x+5x-35\\=x(x-7)+5(x-7)\\=(x-7)(x+5)

So the zeroes are 2+\sqrt{3}\ ,\ 2-\sqrt{3},7\ and\ -5

Q5 If the polynomial x ^4 - 6x ^3 + 16 x^2 - 35 x + 10 is divided by another polynomial x^2 - 2x + k , the remainder comes out to be x + a, find k and a.

Answer: The polynomial division is carried out as follows

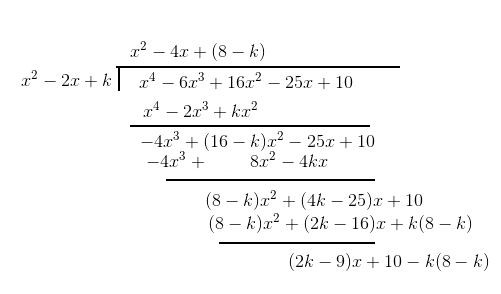
1635919302615

Given the remainder =x+a

The obtained remainder after division is (2k-9)x+10-k(8-k)

now equating the coefficient of x

2k-9=1

which gives the value of k=5

now equating the constants

a=10-k(8-k)=10-5(8-5)=-5

Therefore k=5 and a=-5

More About NCERT Solutions for Class 10 Maths Exercise 2.4:

Exercise 2.4 Class 10 Maths – consists of five problems in this section each containing a few sub-questions. In exercise 2.4 Class 10 Maths question 1 has two subsections where we need to check and demonstrate the relationship between the zeroes and the coefficients in each case. The remaining questions also support the zeros of a polynomial. And the last sum is based on the concept of division of a polynomial. The NCERT solutions for Class 10 Maths exercise 2.4 mainly focused on the zeroes of the polynomial, the relationship between the zeroes, the coefficients of the polynomial and the Division Algorithm. Two questions related to the division algorithm are given in exercise 2.4 Class 10 Maths.

Benefits of NCERT Solutions for Class 10 Maths Exercise 2.4

  • NCERT solutions for Class 10 Maths exercise 2.4 helps in solving and revising all questions of these exercises.
  • If you go through the NCERT solution for Class 10th Maths chapter 2 exercise 2.4, you will be able to get more marks if you practice it thoroughly.
  • Exercise 2.4 Class 10 Maths, is based on zeroes of the polynomial, the relationship between the zeroes, the coefficients of the polynomial and the division Algorithm which are important concepts of the chapter. also find Polynomials class 10 Notes here and use these notes to revise all the concepts discussed in this chapter.

Also see-

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What are terms, degrees and exponents in a polynomial 6x^2 - 5x - 18 ?

This ex 2.4 class 10 discussed concepts of  terms, degrees and exponents in a polynomial. Practice the problems discussed in it to command the concepts. as per the above problem:

Terms : 6x^2, 5x, 18 

Degree : 2 

Exponents : 2 and 1 

2. What is a quadratic polynomial?

The class 10 maths ex 2.4  explains the concepts related to quadratic polynomial. A quadratic polynomial is nothing but a polynomial with degree two. The general form of a quadratic polynomial is ax^2 + bx + c = 0 where a, b, c are real numbers 

3. Check whether the polynomial 5x^2 + 6x + 54 = 0 a quadratic polynomial.

The concepts related to quadratic polynomial are discussed in class 10 ex 2.4. Practice the problems discussed in this exercise to command these concepts. as per this problem the maximum index here is 2 . Also it is in the form of ax^2 + bx + c = 0. 

Therefore 5x^2 + 6x + 54 = 0 is a quadratic polynomial. 

4. Factorize the polynomial n^2 - 10n + 24 .

n^2 - 10n + 24 = n^2 - 4n - 6n + 24 

= n(n - 4) - 6(n - 4) 

= (n - 4)(n - 6) 

5. Is 9 a polynomial?

The number 9 can be written as 9x^0 which is a polynomial. Therefore 9 is a polynomial.

6. What is the division algorithm according to NCERT solutions for Class 10 Maths chapter 2 exercise 2.4 ?

If p(x) and g(x) are any two polynomials where g(x) ≠ 0, p(x) = g(x) × q(x) + r(x).

That is Dividend = Divisor × Quotient + Remainder

7. How many questions and what sort of questions are covered within the NCERT solutions for Class 10 Maths chapter 2 exercise 2.4?

NCERT solutions for Class 10 Maths chapter 2 exercise 2.4  consists of five problems and the questions are based on the concept of the division algorithm, to verify and prove the relationship between the zeroes, the coefficients and the zeros of a polynomial. 

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:02 December,2024 - 16 December,2024

Himachal Pradesh Board of Secondary Education 12th Examination

Application Date:02 December,2024 - 16 December,2024

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Digital Banking Business Model
 Via State Bank of India
Business Analytics Foundations
 Via PW Skills
Full-Stack Android Development
 Via Masai School
Data Science for Beginners
 Via Board Infinity
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:18 PM IST :
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST

Stay up-to date with CBSE Class 10th News

Back to top