NCERT Solutions for Exercise 2.3 Class 10 Maths Chapter 2 - Polynomials
Upcoming Event
CBSE Class 10th Exam Date:01 Jan' 26 - 14 Feb' 26
NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.3 Polynomials
NCERT Solutions for class 10 maths ex 2.3 Polynomials is discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Exercise 2.3 of Class 10 Maths introduces the notion of polynomials in x with real coefficients, the notion of polynomials of degrees 1, 2, 3, quadratic equation, and many more with numerical problems on the Polynomials chapter.
The Class 10th Maths chapter 2 exercise 2.3 moves towards the topics like the class of addition, subtraction and multiplication of polynomials. Also, zeroes/roots of a polynomial function f(x). Also students can find all exercise listed below, practice them to command the maths concepts.
Access Exercise 2.3 Class 10 Maths Answers
Polynomials Class 10 Maths Chapter 2 Excercise: 2.3
Answer: The polynomial division is carried out as follows
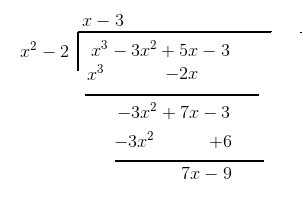
The quotient is x-3 and the remainder is 7x-9
Answer:
The division is carried out as follows
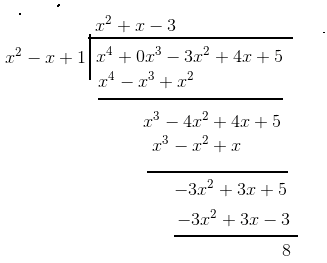
The quotient is $x^2+x-3$
and the remainder is 8
Answer: The polynomial is divided as follows
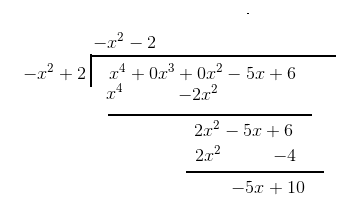
The quotient is $-x^2-2$ and the remainder is $-5x+10$
$t^2 - 3, 2t^4 + 3t^3 - 2t^2 - 9t - 12$
Answer:
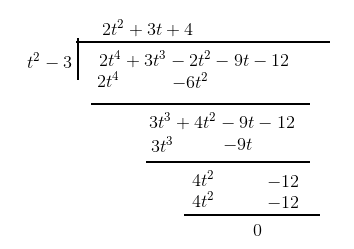
After dividing we got the remainder as zero. So $t^2 - 3$ is a factor of $2t^4 + 3t^3 - 2t^2 - 9t - 12$
$x^2 + 3x + 1, 3x^4 + 5x^3 - 7x^2 + 2x + 2$
Answer: To check whether the first polynomial is a factor of the second polynomial we have to get the remainder as zero after the division
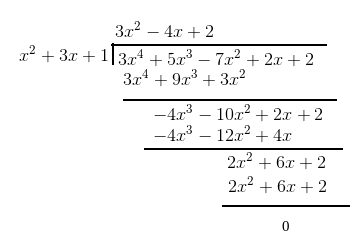
After division, the remainder is zero thus $x^2+3x+1$ is a factor of $3x^4 + 5x^3 - 7x^2 + 2x + 2$
Q2 (3) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial: $x^3 - 3x + 1, x^5 - 4x^3 + x^2 + 3x + 1$
Answer: The polynomial division is carried out as follows
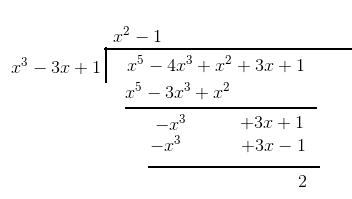
The remainder is not zero, there for the first polynomial is not a factor of the second polynomial
Q3 Obtain all other zeroes of $3x^4 + 6x^3 - 2x^2 - 10x - 5$ , if two of its zeroes are $\sqrt {\frac5{3}} \: \:and \: \: - \sqrt {\frac{5}{3}}$
Answer:
Two of the zeroes of the given polynomial are $\sqrt {\frac5{3}} \: \:and \: \: - \sqrt {\frac{5}{3}}$ .
Therefore two of the factors of the given polynomial are $x-\sqrt{\frac{5}{3}}$ and $x+\sqrt{\frac{5}{3}}$
$(x+\sqrt{\frac{5}{3}})\times (x-\sqrt{\frac{5}{3}})=x^{2}-\frac{5}{3}$
$x^{2}-\frac{5}{3}$ is a factor of the given polynomial.
To find the other factors we divide the given polynomial with $3\times (x^{2}-\frac{5}{3})=3x^{2}-5$
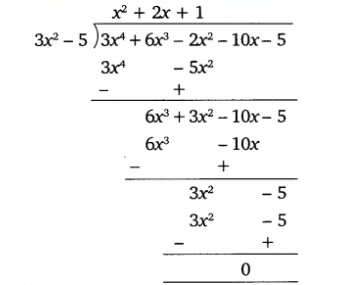
The quotient we have obtained after performing the division is $x^{2}+2x+1$
$\\x^{2}+2x+1\\ =x^{2}+x+x+1\\ =x(x+1)+(x+1)\\ =(x+1)^{2}$
(x+1) 2 = 0
x = -1
The other two zeroes of the given polynomial are -1.
Answer: Quotient = x-2
remainder =-2x+4
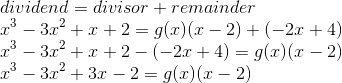
$g(x)=\frac{x^3-3x^2+3x-2}{x-2}$
Carrying out the polynomial division as follows
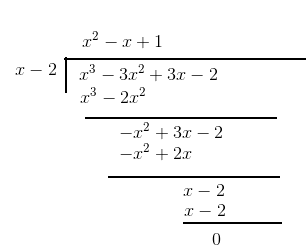
$g(x)={x^2-x+1}$
Answer: deg p(x) will be equal to the degree of q(x) if the divisor is a constant. For example
$\\p(x)=2x^2-2x+8\\q(x)=x^2-x+4\\g(x)=2\\r(x)=0$
Q5 (2) Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and deg q(x) = deg r(x)
Answer: Example for a polynomial with deg q(x) = deg r(x) is given below
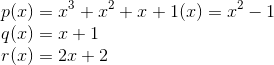
Answer:
example for the polynomial which satisfies the division algorithm with r(x)=0 is given below
$\\p(x)=x^3+3x^2+3x+5\\q(x)=x^2+2x+1\\g(x)=x+1\\r(x)=4$
More About NCERT Solutions for Class 10 Maths Chapter 2 Exercise 2.3
The problems from the concepts of division of polynomial p(x) with polynomial g(x) are covered in exercise 2.3 Class 10 Maths. The Introductory numerical questions of NCERT solutions for Class 10 Maths chapter 2 exercise 2.3 is to represent the numerical problems of finding quotient and remainder. And later on questions of Class 10 Maths chapter 2 exercise 2.3 is to find the polynomial if Quotient and remainder is given.
Also Read| Polynomials Class 10 Notes
Key Features of NCERT Solutions for Class 10 Maths Chapter 2 Exercise 2.3
The solved example before the exercise 2.3 Class 10 Maths and the NCERT solutions for Class 10 Maths chapter 2 exercise 2.3 are important as it covers questions from the basic division of Polynomials
If students can solve each and every question of this exercise 2.3 Class 10 Maths he will be able to grasp the factorization concept of the polynomial as given in Class 10th Maths chapter 2 exercise 2.4
For Class 10 final exams students may get a short answer or long answer questions from the type covered in the Class 10 Maths chapter 2 exercise 2.3
Also see-
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions
Frequently Asked Questions (FAQs)
Q: Define Polynomial?
A:
Polynomial '' comes from the word ‘Poly’ (Meaning Many) and ‘nomial’ (in this case meaning Term)-so it means many terms.
Q: Can a in polynomial ax² + bx + c be equal to zero?
A:
No, a ≠ 0 because it will turn into a linear equation
Q: What happens when zeroes of quadratic equation are equal?
A:
When ax² + bx + c =0 has roots/zeros α and β if they are equal, then sign of a (coef of x²) and c (constant term) must be equal
Q: What is the formula of sum of roots of Polynomial ax² + bx + c =0?
A:
sum of roots = α + β = -(b/a).
Q: What is the formula of Product of roots of Polynomial ax² + bx + c =0?
A:
Product of roots = α * β = (c/a)
Q: What does a polynomial with degree = 3 called?
A:
A polynomial with degree = 3 is called Cubic polynomial
Q: What is division algorithm in Polynomial?
A:
Ans Consider the functions, f(x) and g(x) are any two polynomials with for any value of x, g(x) ≠ 0, then we have derived an expression-
f(x) = g(x) × q(x) + r(x)
Dividend = Divisor * Quotient + Remainder
Q: What happens when a polynomial is multiplied by itself?
A:
Each term of the first polynomial is multiplied by each term of the second polynomial when the two polynomials are multiplied.
Articles
Related Stories
|
Upcoming School Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 10th
On Question asked by student community
Have a question related to CBSE Class 10th ?
Hi! If you’re looking for the Class 11 English half yearly question paper for 2025-26 (CBSE board), you’ll find the right resource once you check the link provided from Careers360. Solving previous or sample papers is a smart way to prepare, as it helps you understand the question types, marking scheme, and important topics. This practice will boost your confidence and help you manage your time well in the actual exam.
https://school.careers360.com/boards/cbse/cbse-class-11-half-yearly-sample-papers-2025-26
Hi dear candidate,
Could you please specify us the board of education for which you need the half yearly question papers of class X so that we can help you further.
Below are few links which may help you and it has all the subjects with English as well:
CBSE Class 10 Half Yearly Exam Question Paper 2025-26 with Answer Key & Analysis
ICSE Class 10 Half Yearly Sample Papers 2025-26 PDF (All Subjects)
BEST REGARDS
Hi dear candidate,
Can you please specify the board of education or state for which you need to know the exam pattern and syllabus so that we can guide you accordingly.
Since, most of the boards uses NCERT as base syllabus, you can refer to the link below:
NCERT Syllabus for Class 10 – All Subjects PDF Download 2025-26
Exam pattern:
CBSE 10th New Exam Pattern 2026- Marking Scheme, Subject-Wise Exam Pattern
BEST REGARDS
The CBSE Class 10th Board Exams for the 2026 session will follow the revised curriculum, emphasizing competency-based questions.
-
Conducting Body: Central Board of Secondary Education (CBSE).
-
Exam Period: The main theory exams are typically held between February and April 2026.
-
Grading: Based on marks in five main subjects plus internal assessment marks (often 20 marks per subject) provided by the school.
-
Passing Criteria: You must achieve at least 33% overall in each subject (theory + practical/internal assessment combined) to be declared pass.
Key Preparation Strategy
The most crucial element of your preparation is understanding the exam structure:
-
Syllabus: Strictly adhere to the rationalized syllabus released by CBSE for the 2025-26 academic year.
-
Practice: Your primary resource should be the latest sample papers and previous year question papers. These accurately reflect the format and types of competency questions being asked.
For the most comprehensive and official announcements, including the detailed time table and access to crucial practice materials, always check the official board updates, as tracked by Careers360: https://school.careers360.com/exams/cbse-class-10th .
HELLO,
If you want admission to 9th grade under the CBSE board in Andhra Pradesh , visit nearby CBSE affiliated schools during the admission period that is generally from January to April or you can check the official websites of the schools in which you are interested for admission if they are accepting the admissions now .
After deciding the school and getting information about admission deadline from the school you can fill out the admission form with documents submission like your previous report card , transfer certificate and birth certificate , they make take entrance test or interview to confirm your admission
To know more visit :- https://school.careers360.com/schools/cbse-schools-in-andhra-pradesh
Hope this Helps!
Popular CBSE Class 10th Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
CBSE Class 10th Notifications
Never miss an CBSE Class 10th update
Get timely CBSE Class 10th updates directly to your inbox. Stay informed!