Integrals 12th Notes - Free NCERT Class 12 Maths Chapter 7 Notes - Download PDF

Integrals Class 12 Notes PDF Download

Use the link below to download the PDF version of NCERT Notes Class 12 Maths Chapter 7 Integrals for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Notes for Class 12 Chapter 7 Integrals

Adding or summing up the small parts to find the whole sum of the function is the basic meaning of integral calculus.

Indefinite integrals and definite integrals are the two types of integrals that are found in integral calculus.

Indefinite Integral

Thus, the formula that gives this anti-derivative is called the indefinite integral.

Integration as an Inverse Process of Differentiation

Integration is defined as the inverse of differentiation. Here, we are given a function and asked to find its primitive (the original function). Such a process is called an anti-derivative or indefinite integral.

Let us see an example:

We know that

$\frac{d}{d x}(\sin x+c)=\cos x$ or, $\int \cos x d x=\sin x+c$

Here, the actual function is “sinx + c”. Using the indefinite integral, we found the actual equation from the derived one.

Thus, we came to know that the integration of some functions is written as

$\int f(x) d x=F(x)+c$

Here, f(x) is “integrand”, f(x)dx is “element of integration”, $x$ is “variable of integration” and “c” is the integration constant.

Some of the formulas are listed below, which will help us to solve the problems.

$\begin{aligned}
& \int x^n d x=\frac{x^{n+1}}{n+1}+c,(n \neq-1) \\
& \int d x=x+c \\
& \int \cos x d x=\sin x+c \\
& \int \sin x d x=-\cos x+c \\
& \int \sec ^2 x d x=\tan x+c \\
& \int \operatorname{cosec}^2 x d x=-\cot x+c \\
& \int \sec x \tan x=\sec x+c \\
& \int \operatorname{cosec} x \cot x=-\operatorname{cosec} x+c \\
& \int \frac{d x}{\sqrt{1-x^2}}=\sin ^{-1} x+c \\
& \int \frac{d x}{\sqrt{1-x^2}}=-\cos ^{-1} x+c \\
& \int \frac{d x}{1+x^2}=\tan ^{-1} x+c \\
& \int \frac{d x}{1+x^2}=-\cot ^{-1} x+c \\
& \int \frac{d x}{x \sqrt{x^2-1}}=\sec ^{-1} x+c \\
& \int \frac{d x}{x \sqrt{x^2-1}}=-\operatorname{cosec}^{-1}+c \\
& \int e^x d x=e^x+c \\
& \int \frac{1}{x} d x=\log |x|+c \\
& \int a^x d x=\frac{a^x}{\log a}+c
\end{aligned}$

Geometrical Interpretation of Indefinite Integral

Let us assume that y=f(x) be a curve such that $f^{\prime}(x)=2 x \Rightarrow f(x)=x^2+c$

Now, if we give values like 4, 3, 2, 1, 0, -1, -2, -3 to the arbitrary constant c, then the equation will give

$y=x^2+4, x^2+3, x^2+2, x^2+1, x^2, x^2-1, x^2-2, x^2-3$ṣ

having loci as a parabola.

Thus, the equation $\int f(x) d x=F(x)+c=y$ represents a family of curves.

Some properties of the indefinite integral

Here we shall derive some properties of indefinite integrals.

(I) The processes of integration and differentiation is the inverse of each other in the sense of the following results:

$\frac{d}{d x} \int f(x) d x=f(x)$ and $\int f^{\prime}(x) d x=f(x)+c$

where c is the arbitrary constant.

(II) Two indefinite integrals with the same derivative lead to the same family of curves; thus, they are equivalent.

$\frac{d}{d x} \int f(x) d x=\frac{d}{d x} \int g(x) d x$

(III) $\int[f(x)+g(x)] d x=\int f(x) d x+\int g(x) d x$
$(I V)$ For any real number $\mathrm{k}, \int k f(x) d x=k \int f(x) d x$

(V) Using properties (III) and (IV) can be generalised to a finite number of functions $f_1, f_2, f_3, …, f_n$ and the real numbers $k_1, k_2, k_3, …, k_n$ give

$\begin{aligned} & \int\left[k_1 f_1(x)+k_2 f_2(x)+\ldots k_n f_n(x)\right] d x \\ = & \int k_1 f_1(x) d x+\int k_2 f_2(x) d x+\ldots \int k_n f_n(x) d x\end{aligned}$

Example:

Find the anti-derivative (integral) of $\frac{1}{x}, \quad x \neq 0$
Solution:
We know that $\frac{d}{d x}(\log x)=\frac{1}{x}, x>0$ and $\frac{d}{d x}(\log (-x))=\frac{1}{-x}(-1)=\frac{1}{x}, x<0$ Thus combining the above $\frac{d}{d x} \log x=\frac{1}{x}, x \neq 0$ Therefore $\frac{1}{x} d x=\log |x|+c$

Methods of Integration

We have many ways of solving integration. Mostly, we solve by using:

1. Integration by substitution

2. Integration by Partial Fraction

3. Integration by Parts

Integration by Substitution

The given integral $\int f(x) d x$ can be transferred into another form by changing the independent variable x to t by substituting $\mathrm{x}=\mathrm{g}(\mathrm{t})$.

Let us assume that

$I=\int f(x) d x$

Substitute

x=g(t), so that dx/dt=g'(t)

Then we write dx=g’(t) dt

Thus $\quad I=\int f(x) d x=\int f(g(t)) g^{\prime}(t) dt$

Example: Integrate w.r.t x, sin mx

Solution:

We know that by differentiating mx, we get m. Thus, we can substitute mx = t so that mdx =dt

Thus $\int \sin (m x) d x=\int \frac{1}{m} \sin (t) d t=-\frac{1}{m} \cos t+c=-\frac{1}{m} \cos m x+c$

Integration by Trigonometric Identities

The identities are used to find the integral when integration involves some trigonometric functions.

Example: Find $\int \cos ^2 x d x$
Solution: We know that

$\cos ^2 x=\frac{1+\cos 2 x}{2}$

Using this, we get that

$\cos ^2 x d x=\frac{1}{2}(1+\cos 2 x) d x=\frac{1}{2}[d x+\cos 2 x d x]=\frac{x}{2}+\frac{1}{4} \sin 2 x+c$

Integrals of Some Particular Function

Some of the formulas are listed below

$\begin{aligned}
& \int \frac{d x}{x^2-a^2} d x=\frac{1}{2 a} \log \frac{|x-a|}{|x+a|}+c \\
& \int \frac{d x}{a^2-x^2}=\frac{1}{2 a} \log \frac{|a+x|}{|a-x|}+c \\
& \int \frac{d x}{x^2+a^2}=\frac{1}{a} \tan ^{-1} \frac{x}{a}+c \\
& \int \frac{d x}{\sqrt{x^2-a^2}}=\log \left|x+\sqrt{x^2-a^2}\right|+c \\
& \int \frac{d x}{\sqrt{x^2+a^2}}=\log \left|x+\sqrt{x^2+a^2}\right|+c \\
& \int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+c
\end{aligned}$

Let us see an example

$\begin{aligned}
& \int \frac{d x}{\left(4+9 x^2\right)} d x \\
& =\int \frac{d x}{9\left(\frac{4}{9}+x 2\right)}
\end{aligned}$

Now using a special formula

$\begin{aligned}
& \int \frac{d x}{x^2+a^2}=\frac{1}{a} \tan ^{-1} \frac{x}{a}+c \\
& =\frac{1}{9} \int \frac{d x}{x^2+\left(\frac{2}{3}\right)^2} \\
& =\frac{1}{9} \frac{1}{2 / 3} \tan ^{-1} \frac{3 x}{2}+c \\
& =\frac{1}{6} \tan ^{-1} \frac{3 x}{2}+c
\end{aligned}$

Integration by Partial Fraction

The integration of a rational function can be solved by using partial fractions.

$\begin{array}{|l|l|l|}
\hline \text { S.No. } & \text { Form of a rational function } & \text { Formation of a partial function } \\
\hline 1 & \frac{p x+q}{(x-a)(x-b)}, a \neq b & \frac{A}{x-a}+\frac{B}{x-b} \\
\hline 2 & \frac{p x+q}{(x-a)^2} & \frac{A}{x-a}+\frac{B}{(x-a)^2} \\
\hline 3 & \frac{p x^2+q x+r}{(x-a)(x-b)(x-c)} & \frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c} \\
\hline 4 & \frac{p x^2+q x+r}{(x-a)^2(x-b)} & \frac{A}{x-a}+\frac{B}{(x-a)^2}+\frac{C}{x-b} \\
\hline 5 & \frac{p x^2+q x+r}{(x-a)\left(x^2+b x+c\right)} & \frac{A}{x-a}+\frac{B x+c}{x^2+b x+c} \\
\hline
\end{array}$
Let us see the following example
$\begin{aligned}
& \int \frac{x^2}{x^2+x+6} d x \\
& =\int\left(1-\frac{x-6}{x^2+x+6} d x\right. \\
& =\int d x-\int \frac{x-6}{x 2+x+6} d x \\
& =x-\frac{9}{5} \int \frac{d x}{x+3}+\frac{4}{5} \int \frac{d x}{x-2} \\
& =x-\frac{9}{5} \ln |x+3|+\frac{4}{5} \ln |x-2|+c
\end{aligned}$

Integration by Parts

The ILATE rule needs to be followed while doing integration by parts. According to the ILATE rule, we can determine which function will be the 1st function and which will be the 2nd function.

ILATE

I → Inverse function

L → Logarithmic function

A → Algebraic function

T → Trigonometric function

E → Exponential function

From the above rule, as an example, we can say that there are two functions, like trigonometric functions and logarithmic functions. The logarithmic function will be treated as the first function, and the trigonometric function will be treated as the second function.

The general expression follows as

$\int f(x) g(x) d x=f(x) \int g(x) d x-\int\left[\left\{\int g(x) d x\right\} \frac{d}{d x} f(x)\right] dx$

“The integral of the product of two functions = (1st function) × (integral of the 2nd function) – Integral of [(differential coefficient of the 1st function) × (integral of the 2nd function)]”

Example: Solve $\int \ln x d x$
Solution:
$\begin{aligned}
& \int \ln x \cdot 1 d x \\
& \Rightarrow \ln x \int 1 d x-\int\left[\left(\int 1 d x\right) \frac{d}{d x}(\ln x)\right] d x \\
& \Rightarrow x \ln x-\int x \cdot \frac{1}{x} d x \\
& \Rightarrow x \ln x-x+c
\end{aligned}$

Integration of special types of functions
The formulas are listed below

$\begin{aligned}
& \int \sqrt{x^2+a^2} d x=\frac{1}{2} x \sqrt{x^2+a^2}+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+c \\
& \int \sqrt{x^2-a^2} d x=\frac{1}{2} x \sqrt{x^2-a^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+c
\end{aligned}$

Definite Integral

In the indefinite, we saw that the result of the integration was not a unique value. But here indefinite integral we will find a unique value, and it is well defined within a limited boundary. Generally, the definite integral is denoted by

$\int_a^b f(x) d x$

Her “a” is the lower limit, and “b” is the upper limit of the integral. The value of the definite integral is computed by F(b) - F(a).

Basically, in Definite integral consists of two cases as discussed below:

Definite Integral as a Limit of the Sum

If the definite integral $\int_a^b f(x) d x$

is the area bounded by the curve y = f(x), the ordinates x = a, x = b and the x-axis. To evaluate this area, consider the region PRSQP between this curve, the x-axis, and the ordinates x = a and x =b

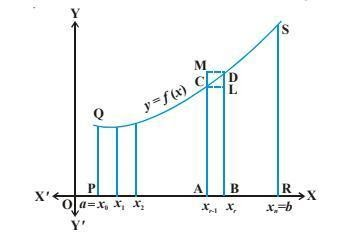
From the figure, we find the general equation of the definite integral as a limit of a sum

$\begin{aligned}
&\begin{aligned}
\int_a^b f(x) d x & =h[f(a)+f(a+h)+\ldots+f(a+(n-1) h] \\
\Rightarrow \int_a^b f(x) d x & =\frac{(b-a)}{n}[f(a)+f(a+h)+\ldots+f(a+(n-1) h]
\end{aligned}\\
&\text { Where } h=\frac{b-a}{n} \rightarrow 0 \text { as } n \rightarrow \infty
\end{aligned}$

Some Properties of the Definite Integral

$P_0: \int_a^b f(x) d x=\int_a^b f(t) d t$
$P_1: \int_a^b f(x) d x=-\int_b^a f(x) d x ;$ in particular, $\int_a^a f(x) d x=0$
$P_2: \int_a^b f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$
$P_3: \int_a^c f(x) d x=\int_a^c f(a+b-x) d x$
$P_4: \int_0^b f(x) d x=\int_0^b f(b-x) d x$
$P_5: \int_0^{2 b} f(x) d x=\int_0^b f(x) d x+\int_0^b f(2 b-x) d x$
$P_6: \int_0^{2 b} f(x) d x=2 \int_0^b f(x) d x$ if $f(2 b-x)=f(x)$
and $\int_0^{2 b} f(x) d x=0 \quad$ if $\quad f(2 b-x)=-f(x)$
$P_7:(i) \int_{-a}^a f(x) d x=2 \int_0^a f(x) d x$, if f is even function, i.e., if $\mathrm{f}(-\mathrm{x})=\mathrm{f}(\mathrm{x})$
(ii) $\int_{-a}^a f(x) d x=0$, if f is odd function, i.e., $\mathrm{f}(-\mathrm{x})=-\mathrm{f}(\mathrm{x})$

Let us see an example

$\begin{aligned}
& \int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x \\
& \text { Let } \int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x=I-\cdots\cdots (1) \\
& I=\int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin \left(\frac{\pi}{2}-x\right)}}{\sqrt{\sin \left(\frac{\pi}{2}-x\right)}+\sqrt{\cos \left(\frac{\pi}{2}-x\right)}} d x \\
& I=\int_0^{\frac{\pi}{2}} \frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x\cdots\cdots\cdots (2)
\end{aligned}$
Now $(1)+(2)$
$\begin{aligned}
& \int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x+\int_0^{\frac{\pi}{2}} \frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x=2 I \\
& 2 I=\int_0^{\frac{\pi}{2}} d x \\
& I=\frac{\pi}{4}
\end{aligned}$

This brings us to the end of the chapter.

Integrals: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 12 chapter 7 Integrals:

Question 1: The integral $\int_{-1}^{\frac{3}{2}}\left(\left|\pi^2 x \sin (\pi x)\right|\right) \mathrm{dx}$ is equal to:

Solution:

$\begin{aligned} & I=\int_{-1}^{3 / 2}\left|\pi^2 x \sin (\pi x)\right| d x \\ &=\int_{-1}^1\left|\pi^2 x \sin (\pi x)\right| d x+\int_1^{3 / 2}\left|\pi^2 x \sin (\pi x)\right| d x \\ &=2 \int_0^1\left|\pi^2 x \sin (\pi x)\right| d x-\pi^2 \int_1^{3 / 2}|x \sin (\pi x)| d x\end{aligned}$

$\begin{aligned} & =2 \pi^2 \int_0^1|x \sin (\pi x)| d x-\pi^2 \int_1^{3 / 2}|x \sin (\pi x)| d x \\ & \because \int x \sin (\pi x) d x=x\left(\frac{-\cos \pi x}{\pi}\right)-\int \frac{-\cos \pi x}{\pi} d x \\ & =-\frac{x}{\pi} \cos \pi x+\frac{1}{\pi^2} \sin \pi x+C \\ & \therefore \quad I=2 \pi^2\left(\frac{1}{\pi}\right)-\pi^2\left(-\frac{1}{\pi^2}-\frac{1}{\pi}\right) \\ & =2 \pi+1+\pi \\ & =3 \pi+1\end{aligned}$

Hence, the correct answer is $3 \pi+1$.

Question 2: The value of $\int_{-1}^1 \frac{(1+\sqrt{|x|-x}) e^x+(\sqrt{|x|-x}) e^{-x}}{e^x+e^{-x}} d x$ is equal to:

Solution:

$\begin{aligned} & \mathrm{I}=\int_{-1}^1 \frac{(1+\sqrt{|-\mathrm{x}|-(-\mathrm{x})}) \mathrm{e}^{-\mathrm{x}}+(\sqrt{|-\mathrm{x}|-(-\mathrm{x})}) \mathrm{e}^{-(-\mathrm{x})}}{\mathrm{e}^{-\mathrm{x}}+\mathrm{e}^{-(-\mathrm{x})}} \mathrm{dx} \\ & \Rightarrow \mathrm{I}=\int_{-1}^1 \frac{(1+\sqrt{|\mathrm{x}|+\mathrm{x}}) \mathrm{e}^{-\mathrm{x}}+(\sqrt{|\mathrm{x}|+\mathrm{x}}) \mathrm{e}^{\mathrm{x}}}{\mathrm{e}^{\mathrm{-x}}+\mathrm{e}^{\mathrm{x}}} \mathrm{dx}\end{aligned}$

$\begin{aligned} & \Rightarrow 2 \mathrm{I}=\int_{-1}^1 \frac{(1+\sqrt{|\mathrm{x}|+\mathrm{x}}+\sqrt{|\mathrm{x}|-\mathrm{x}})\left(\mathrm{e}^{\mathrm{x}}+\mathrm{e}^{-\mathrm{x}}\right)}{\left(\mathrm{e}^{\mathrm{x}}+\mathrm{e}^{-\mathrm{x}}\right)} \mathrm{dx} \\ & \Rightarrow 2 \mathrm{I}=\int_{-1}^1(1+\sqrt{|\mathrm{x}|+\mathrm{x}}+\sqrt{|\mathrm{x}|-\mathrm{x}}) \mathrm{dx}\end{aligned}$

$\begin{aligned} & \Rightarrow 2 \mathrm{I}=2 \int_0^1(1+\sqrt{|\mathrm{x}|+\mathrm{x}}+\sqrt{|\mathrm{x}|-\mathrm{x}}) \mathrm{dx} \\ & \Rightarrow 2 \mathrm{I}=2 \int_0^1(1+\sqrt{2 \mathrm{x}}+\sqrt{0}) \mathrm{dx}\end{aligned}$

$\begin{aligned} & \Rightarrow \mathrm{I}=\int_0^1(1+\sqrt{2 \mathrm{x}}) \mathrm{dx}=\left[\mathrm{x}+\frac{2 \sqrt{2}}{3} \mathrm{x}^{3 / 2}\right]_0^1 \\ & \Rightarrow \mathrm{I}=\frac{2 \sqrt{2}}{3}+1\end{aligned}$

Hence, the correct answer is $\frac{2 \sqrt{2}}{3}+1$.

Question 3: The integral $\int_0^\pi \frac{8 x d x}{4 \cos ^2 x+\sin ^2 x}$ is equal to

Solution:

$I=\int_0^\pi \frac{8 x d x}{4 \cos ^2 x+\sin ^2 x}$

Apply property
$I=\int_0^\pi \frac{8(\pi-x) d x}{4 \cos ^2 x+\sin ^2 x}$

Add
$\begin{aligned}
& 2 I=\int_0^\pi \frac{8 \pi}{4 \cos ^2 x+\sin x} d x \\
& I=4 \pi \int_0^\pi \frac{1}{4 \cos ^2 x+\sin ^2 x}
\end{aligned}$

$\begin{aligned} & \because \frac{1}{4 \cos ^2 x+\sin ^2 x}=\frac{1}{4 \cos ^2(\pi-x)+\sin ^2(\pi-x)} \\ & \therefore I=4 \pi \times 2 \int_0^{\pi / 2} \frac{1}{4 \cos ^2 x+\sin ^2 x} d x \\ & =8 \pi \int_0^{\pi / 2} \frac{\sec ^2 x d x}{4+\tan ^2 x} \\ & \text { let } \tan x=t \\ & \sec ^2 x d x=d t \\ & =8 \pi \int_0^{\infty} \frac{d t}{4+t^2} \\ & =\frac{8 \pi}{2}\left[\tan ^{-1} t\right]_0^{\infty} \\ & = \frac{8 \pi}{2}(\pi / 2-0) \\ & = \frac{4 \pi^2}{2} = 2 \pi^2\end{aligned}$

Hence, the correct answer is $2 \pi^2$.

NCERT Class 12 Maths Notes – Chapter-Wise Links

To help students in their preparation, Careers360 has compiled all Class 12 Maths NCERT notes in one place for easy and quick access.

Subject-Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 12 Solutions
• NCERT Exemplar Class 12 Maths
• NCERT Exemplar Class 12 Physics
• NCERT Exemplar Class 12 Chemistry
• NCERT Exemplar Class 12 Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions of class 12.

• NCERT Solutions for Class 12 Mathematics
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for Class 12 Biology

NCERT Books and NCERT Syllabus

Before starting a new academic year, students should refer to the latest syllabus to see the chapters they’ll be studying. Given below are the updated syllabus links along with some reference books.

• NCERT Books Class 12 Maths
• NCERT Syllabus Class 12 Maths
• NCERT Books Class 12
• NCERT Syllabus Class 12