• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Miscellaneous Exercise Chapter 9 Class 12 - Differential Equations

NCERT Solutions for Miscellaneous Exercise Chapter 9 Class 12 - Differential Equations

Edited By Ramraj Saini | Updated on Dec 04, 2023 01:29 PM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 12 Chapter 9 Miscellaneous Exercise

NCERT Solutions for miscellaneous exercise chapter 9 class 12 Differential Equations are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. At the end of all the chapters of NCERT Class 12 Maths book, there is an exercise known as miscellaneous exercise. This covers questions from the whole chapter. NCERT solutions for Class 12 Maths chapter 9 miscellaneous exercise take a tour through all the concepts covered in this NCERT chapter. Class 12 Maths chapter 9 miscellaneous exercise solutions are a bit more lengthy compared to other exercises of differential equations. Class 12 Maths chapter 9 miscellaneous solutions covers the complete chapter through questions. If one student is able to solve miscellaneous exercise chapter 9 Class 12 without looking to the solution, then it implies he has understood the concepts covered in the chapter. The ideas covered in the last 6 exercises are used in the NCERT solutions for Class 12 Maths chapter 9 miscellaneous exercise.

This Story also Contains
  1. NCERT Solutions For Class 12 Chapter 9 Miscellaneous Exercise
  2. More About NCERT Solutions for Class 12 Maths Chapter 9 Miscellaneous Exercise
  3. Also Read| Differential Equations Class 12th Notes
  4. Benefits of NCERT Solutions for Class 12 Maths Chapter 9 Miscellaneous Exercise.
  5. By going through the Class 12 Maths chapter 9 miscellaneous exercise solutions students can have better exposure to the concepts detailed in the chapter.
  6. All the questions in the miscellaneous exercise chapter 9 Class 12 are important and are important from an exam point of view.
  7. Key Features Of NCERT Solutions For Class 12 Chapter 9 Miscellaneous Exercise
  8. NCERT Solutions Subject Wise
  9. Subject Wise NCERT Exemplar Solutions

Miscellaneous exercise class 12 chapter 9 are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise enumerated in NCERT Book together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Differential Equations Class 12 Chapter 9 -Miscellaneous Exercise

Question:1 Indicate Order and Degree.

(i) \frac{d^2y}{dx^2} + 5x \left (\frac{dy}{dx} \right )^2-6y = \log x

Answer:

Given function is
\frac{d^2y}{dx^2} + 5x \left (\frac{dy}{dx} \right )^2-6y = \log x
We can rewrite it as
y''+5x(y')^2-6y = \log x
Now, it is clear from the above that, the highest order derivative present in differential equation is y''

Therefore, the order of the given differential equation \frac{d^2y}{dx^2} + 5x \left (\frac{dy}{dx} \right )^2-6y = \log x is 2
Now, the given differential equation is a polynomial equation in its derivative y '' and y 'and power raised to y '' is 1
Therefore, it's degree is 1

Question:1 Indicate Order and Degree.

(ii) \left(\frac{dy}{dx} \right )^3 - 4\left(\frac{dy}{dx} \right )^2 + 7y = \sin x

Answer:

Given function is
\left(\frac{dy}{dx} \right )^3 - 4\left(\frac{dy}{dx} \right )^2 + 7y = \sin x
We can rewrite it as
(y')^3-4(y')^2+7y=\sin x
Now, it is clear from the above that, the highest order derivative present in differential equation is y'

Therefore, order of given differential equation is 1
Now, the given differential equation is a polynomial equation in it's dervatives y 'and power raised to y ' is 3
Therefore, it's degree is 3

Question:1 Indicate Order and Degree.

(iii) \frac{d^4 y}{dx^4} - \sin\left(\frac{d^3y}{dx^3} \right ) = 0

Answer:

Given function is
\frac{d^4 y}{dx^4} - \sin\left(\frac{d^3y}{dx^3} \right ) = 0
We can rewrite it as
y''''-\sin y''' = 0
Now, it is clear from the above that, the highest order derivative present in differential equation is y''''

Therefore, order of given differential equation is 4
Now, the given differential equation is not a polynomial equation in it's dervatives
Therefore, it's degree is not defined

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(i) xy = ae^x + be^{-x} + x^2\qquad :\ x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} - xy +x^2 -2 =0

Answer:

Given,

xy = ae^x + be^{-x} + x^2

Now, differentiating both sides w.r.t. x,

x\frac{dy}{dx} + y = ae^x - be^{-x} + 2x

Again, differentiating both sides w.r.t. x,

\\ (x\frac{d^2y}{dx^2} + \frac{dy}{dx}) + \frac{dy}{dx} = ae^x + be^{-x} + 2 \\ \implies x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} = ae^x + be^{-x} + 2 \\ \implies x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} = xy -x^2 + 2 \\ \implies x\frac{d^2y}{dx^2} + 2\frac{dy}{dx} - xy + x^2 + 2

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(ii) y = e^x(a\cos x + b \sin x )\qquad : \ \frac{d^2y}{dx^2} - 2\frac{dy}{dx} + 2y = 0

Answer:

Given,

y = e^x(a\cos x + b \sin x )

Now, differentiating both sides w.r.t. x,

\frac{dy}{dx} = e^x(-a\sin x + b \cos x ) + e^x(a\cos x + b \sin x ) =e^x(-a\sin x + b \cos x ) +y

Again, differentiating both sides w.r.t. x,

\\ \frac{d^2y}{dx^2} = e^x(-a\cos x - b \sin x ) + e^x(-a\sin x + b \cos x ) + \frac{dy}{dx} \\ = -y + (\frac{dy}{dx} -y) + \frac{dy}{dx} \\ \implies \frac{d^2y}{dx^2} - 2\frac{dy}{dx} + 2y = 0

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(iii) y= x\sin 3x \qquad : \ \frac{d^2y}{dx^2} + 9y - 6\cos 3x = 0

Answer:

Given,

y= x\sin 3x

Now, differentiating both sides w.r.t. x,

y= x\sin 3x \frac{dy}{dx} = x(3\cos 3x) + \sin 3x

Again, differentiating both sides w.r.t. x,

\\ \frac{d^2y}{dx^2} = 3x(-3\sin 3x) + 3\cos 3x + 3\cos 3x \\ = -9y + 6\cos 3x \\ \implies \frac{d^2y}{dx^2} + 9y - 6\cos 3x = 0

Therefore, the given function is the solution of the corresponding differential equation.

Question:2 Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.

(iv) x^2 = 2y^2\log y\qquad : \ (x^2 + y^2)\frac{dy}{dx} - xy = 0

Answer:

Given,

x^2 = 2y^2\log y

Now, differentiating both sides w.r.t. x,

\\ 2x = (2y^2.\frac{1}{y} + 2(2y)\log y)\frac{dy}{dx} = 2(y + 2y\log y)\frac{dy}{dx} \\ \implies \frac{dy}{dx} = \frac{x}{y(1+ 2\log y)}

Putting \frac{dy}{dx}\ and \ x^2 values in LHS

\\ (2y^2\log y + y^2)\frac{dy}{dx} - xy = y^2(2\log y + 1)\frac{x}{y(1+ 2\log y)} -xy \\ = xy - xy = 0 = RHS

Therefore, the given function is the solution of the corresponding differential equation.

Question:3 Form the differential equation representing the family of curves given by (x-a)^2 + 2y^2 = a^2 , where a is an arbitrary constant.

Answer:

Given equation is
(x-a)^2 + 2y^2 = a^2
we can rewrite it as
2y^2 = a^2-(x-a)^2 -(i)
Differentiate both the sides w.r.t x
\frac{d\left ( 2y^2 \right )}{dx}=\frac{d(a^2-(x-a)^2)}{dx}
4yy^{'}=4y\frac{dy}{dx}=-2(x-a)\\ \\
(x-a)= -2yy'\Rightarrow a = x+2yy' -(ii)
Put value from equation (ii) in (i)
(-2yy')^2+2y^2= (x+2yy')^2\\ 4y^2(y')^2+2y^2= x^2+4y^2(y')^2+4xyy'\\ y' = \frac{2y^2-x^2}{4xy}
Therefore, the required differential equation is y' = \frac{2y^2-x^2}{4xy}

Question:4 Prove that x^2 - y^2 = c (x^2 + y^2 )^2 is the general solution of differential equation (x^3 - 3x y^2 ) dx = (y^3 - 3x^2 y) dy , where c is a parameter.

Answer:

Given,

(x^3 - 3x y^2 ) dx = (y^3 - 3x^2 y) dy

\implies \frac{ dy}{dx} = \frac{(x^3 - 3x y^2 )}{(y^3 - 3x^2 y)}

Now, let y = vx

\implies \frac{ dy}{dx} = \frac{ d(vx)}{dx} = v + x\frac{dv}{dx}

Substituting the values of y and y' in the equation,

v + x\frac{dv}{dx} = \frac{(x^3 - 3x (vx)^2 )}{((vx)^3 - 3x^2 (vx))}

\\\implies v + x\frac{dv}{dx} = \frac{1 - 3v^2 }{v^3 - 3v}\\ \implies x\frac{dv}{dx} = \frac{1 - 3v^2 }{v^3 - 3v} -v = \frac{1 - v^4 }{v^3 - 3v}

\implies (\frac{v^3 - 3v }{1 - v^4})dv = \frac{dx}{x}

Integrating both sides we get,

1517901119530459

Now, 1517901120316962

1517901121031268

Let 151790112181538

151790112256298

\implies 1517901123344265

\implies 1517901124127226

Now, 1517901124894198

1517901125674574

Let v 2 = p

151790112647622

1517901127259961

1517901128042674

1517901128803851

Now, substituting the values of I 1 and I 2 in the above equation, we get,

1517901129585614

Thus,

1517901130366853

1517901131127676

1517901131975586

1517901132764415

\\ (x^2 - y^2)^2 = C'^4(x^2 + y^2 )^4 \\ \implies (x^2 - y^2) = C'^2(x^2 + y^2 )^2 \\ \implies (x^2 - y^2) = K(x^2 + y^2 )^2, where\ K = C'^2

Question:5 Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.

Answer:

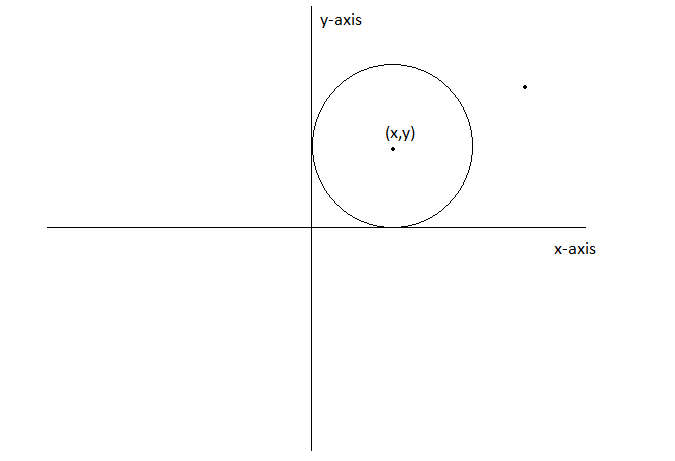
1654780046916 Now, equation of the circle with center at (x,y) and radius r is
(x-a)^2+(y-b)^2 = r^2
Since, it touch the coordinate axes in first quadrant
Therefore, x = y = r
(x-a)^2+(y-a)^2 = a^2 -(i)
Differentiate it w.r.t x
we will get
2(x-a)+2(y-a)y'= 0\\ \\ 2x-2a+2yy'-2ay' = 0\\ a=\frac{x+yy'}{1+y'} -(ii)
Put value from equation (ii) in equation (i)
(x-\frac{x+yy'}{1+y'})^2+(y-\frac{x+yy'}{1+y'})^2=\left ( \frac{x+yy'}{1+y'} \right )^2\\ \\ (x+xy'-x-yy')^2+(y+yy'-x-yy')^2=(x+yy')^2\\ \\ (y')^2(x-y)^2+(x-y)^2=(x+yy')^2\\ \\ (x-y)^2\left ( (y')^2+1 \right )=(x+yy')^2
Therefore, the differential equation of the family of circles in the first quadrant which touches the coordinate axes is (x-y)^2\left ( (y')^2+1 \right )=(x+yy')^2

Question:6 Find the general solution of the differential equation \frac{dy}{dx} + \sqrt{\frac{1 - y^2}{1-x^2}} = 0

Answer:

Given equation is
\frac{dy}{dx} + \sqrt{\frac{1 - y^2}{1-x^2}} = 0
we can rewrite it as
\frac{dy}{dx } =- \sqrt{\frac{1-y^2}{1-x^2}}\\ \\ \frac{dy}{\sqrt{1-y^2}}= \frac{-dx}{\sqrt{1-x^2}}
Now, integrate on both the sides
\sin^{-1}y + C =- \sin ^{-1}x + C'\\ \\ \sin^{-1}y+\sin^{-1}x= C
Therefore, the general solution of the differential equation \frac{dy}{dx} + \sqrt{\frac{1 - y^2}{1-x^2}} = 0 is \sin^{-1}y+\sin^{-1}x= C

Question:7 Show that the general solution of the differential equation \frac{dy}{dx} + \frac{y^2 + y + 1}{x^2 + x + 1} = 0 is given by (x + y + 1) = A (1 - x - y - 2xy) , where A is parameter.

Answer:

Given,

\frac{dy}{dx} + \frac{y^2 + y + 1}{x^2 + x + 1} = 0

1517901142938688

1517901143721318

1517901144865249

Integrating both sides,

15179011455756

1517901146296446

1517901147071246

1517901147830720

1517901148634163

1517901149451944

1517901150235484

1517901151028875

1517901151812195

Let 1517901152593257

1517901153375926

Let A = 1517901154163100 ,

1517901154943810

Hence proved.

Question:8 Find the equation of the curve passing through the point \left(0,\frac{\pi}{4} \right ) whose differential equation is \sin x \cos y dx + \cos x \sin y dy = 0.

Answer:

Given equation is
\sin x \cos y dx + \cos x \sin y dy = 0.
we can rewrite it as
\frac{dy}{dx}= -\tan x\cot y\\ \\ \frac{dy}{\cot y}= -\tan xdx\\ \\ \tan y dy =- \tan x dx
Integrate both the sides
\log |\sec y|+C' = -\log|sec x|- C''\\ \\ \log|\sec y | +\log|\sec x| = C\\ \\ \sec y .\sec x = e^{C}
Now by using boundary conditiond, we will find the value of C
It is given that the curve passing through the point \left(0,\frac{\pi}{4} \right )
So,
\sec \frac{\pi}{4} .\sec 0 = e^{C}\\ \\ \sqrt2.1= e^C\\ \\ C = \log \sqrt2
Now,
\sec y.\sec x= e^{\log \sqrt 2}\\ \\ \frac{\sec x}{\cos y} = \sqrt 2\\ \\ \cos y = \frac{\sec x}{\sqrt 2}
Therefore, the equation of the curve passing through the point \left(0,\frac{\pi}{4} \right ) whose differential equation is \sin x \cos y dx + \cos x \sin y dy = 0. is \cos y = \frac{\sec x}{\sqrt 2}

Question:9 Find the particular solution of the differential equation (1 + e^ {2x} ) dy + (1 + y^2 ) e^x dx = 0 , given that y = 1 when x = 0 .

Answer:

Given equation is
(1 + e^ {2x} ) dy + (1 + y^2 ) e^x dx = 0
we can rewrite it as
\frac{dy}{dx}= -\frac{(1+y^2)e^x}{(1+e^{2x})}\\ \\ \frac{dy}{1+y^2}= \frac{-e^xdx}{1+e^{2x}}
Now, integrate both the sides
\tan^{-1}y + C' =\int \frac{-e^{x}dx}{1+e^{2x}}
\int \frac{-e^{x}dx}{1+e^{2x}}\\
Put
e^x = t \\ e^xdx = dt
\int \frac{dt}{1+t^2}= \tan^{-1}t + C''
Put t = e^x again
\int \frac{-e^{x}dx}{1+e^{2x}} = -\tan ^{-1}e^x+C''
Put this in our equation
\tan^{-1}y = -\tan ^{-1}e^x+C\\ \tan^{-1}y +\tan ^{-1}e^x=C
Now, by using boundary conditions we will find the value of C
It is given that
y = 1 when x = 0
\\ \tan^{-1}1 +\tan ^{-1}e^0=C\\ \\ \frac{\pi}{4}+\frac{\pi}{4}= C\\ C = \frac{\pi}{2}
Now, put the value of C

\tan^{-1}y +\tan ^{-1}e^x=\frac{\pi}{2}
Therefore, the particular solution of the differential equation (1 + e^ {2x} ) dy + (1 + y^2 ) e^x dx = 0 is \tan^{-1}y +\tan ^{-1}e^x=\frac{\pi}{2}

Question:10 Solve the differential equation ye^\frac{x}{y}dx = \left(xe^\frac{x}{y} + y^2 \right )dy\ (y \neq 0)

Answer:

Given,

ye^\frac{x}{y}dx = (xe^\frac{x}{y} + y^2)dy

\\ ye^\frac{x}{y}\frac{dx}{dy} = xe^\frac{x}{y} + y^2 \\ \implies e^\frac{x}{y}[y\frac{dx}{dy} -x] = y^2 \\ \implies \frac{e^\frac{x}{y}[y\frac{dx}{dy} -x]}{y^2} = 1

Let \large e^\frac{x}{y} = t

Differentiating it w.r.t. y, we get,

\\ \frac{d}{dy}e^\frac{x}{y} = \frac{dt}{dy} \\ \implies e^\frac{x}{y}.\frac{d}{dy}(\frac{x}{y}) = \frac{dt}{dy} \\ \implies \frac{e^\frac{x}{y}[y\frac{dx}{dy} -x]}{y^2} =\frac{dt}{dy}

Thus from these two equations,we get,

\\ \frac{dt}{dy} = 1 \\ \implies \int dt = \int dy \\ \implies t = y + C

1517901178627857

Question:11 Find a particular solution of the differential equation (x - y) (dx + dy) = dx - dy, , given that y = -1 , when x = 0 . (Hint: put x - y = t )

Answer:

Given equation is
(x - y) (dx + dy) = dx - dy,
Now, integrate both the sides
Put
(x-y ) = t\\ dx - dy = dt
Now, given equation become
dx+dy= \frac{dt}{t}
Now, integrate both the sides
x+ y + C '= \log t + C''
Put t = x- y again
x+y = \log (x-y)+ C
Now, by using boundary conditions we will find the value of C
It is given that
y = -1 when x = 0
0+(-1) = \log (0-(-1))+ C\\ C = -1
Now, put the value of C

x+y = \log |x-y|-1\\ \log|x-y|= x+y+1
Therefore, the particular solution of the differential equation (x - y) (dx + dy) = dx - dy, is \log|x-y|= x+y+1

Question:12 Solve the differential equation \left[\frac{e^{-2\sqrt x}}{\sqrt x} - \frac{y}{\sqrt x} \right ]\frac{dx}{dy} = 1\; \ (x\neq 0) .

Answer:

Given,

\left[\frac{e^{-2\sqrt x}}{\sqrt x} - \frac{y}{\sqrt x} \right ]\frac{dx}{dy} = 1

1517901190189935

1517901190951594

This is equation is in the form of 1517901191734385

p = 1517901192495126 and Q = 151790119325976

Now, I.F. = 1517901194040946

We know that the solution of the given differential equation is:

1654780149326

151790119561795

1517901196417819

151790119717945

Question:13 Find a particular solution of the differential equation \frac{dy}{dx} + y \cot x = 4x \textup{cosec} x\ (x\neq 0) , given that y = 0 \ \textup{when}\ x = \frac{\pi}{2} .

Answer:

Given equation is
\frac{dy}{dx} + y \cot x = 4x \textup{cosec} x\ (x\neq 0)
This is \frac{dy}{dx} + py = Q type where p =\cot x and Q = 4xcosec x Q = 4x \ cosec x
Now,
I.F. = e^{\int pdx}= e^{\int \cot xdx}= e^{\log |\sin x|}= \sin x
Now, the solution of given differential equation is given by relation
y(I.F.) =\int (Q\times I.F.)dx +C
y(\sin x ) =\int (\sin x\times 4x \ cosec x)dx +C
y(\sin x) =\int(\sin x\times \frac{4x}{\sin x}) +C\\ \\ y(\sin x) = \int 4x + C\\ y\sin x= 2x^2+C
Now, by using boundary conditions we will find the value of C
It is given that y = 0 when x= \frac{\pi}{2}
at x= \frac{\pi}{2}
0.\sin \frac{\pi}{2 } = 2.\left ( \frac{\pi}{2} \right )^2+C\\ \\ C = - \frac{\pi^2}{2}
Now, put the value of C
y\sin x= 2x^2-\frac{\pi^2}{2}
Therefore, the particular solution is y\sin x= 2x^2-\frac{\pi^2}{2}, (sinx\neq0)

Question:14 Find a particular solution of the differential equation (x+1)\frac{dy}{dx} = 2e^{-y} -1 , given that y = 0 when x = 0

Answer:

Given equation is
(x+1)\frac{dy}{dx} = 2e^{-y} -1
we can rewrite it as
\frac{e^ydy}{2-e^y}= \frac{dx}{x+1}\\
Integrate both the sides
\int \frac{e^ydy}{2-e^y}= \log |x+1|\\
\int \frac{e^ydy}{2-e^y}
Put
2-e^y = t\\ -e^y dy = dt
\int \frac{-dt}{t}=- \log |t|
put t = 2- e^y again
\int \frac{e^ydy}{2-e^y} =- \log |2-e^y|
Put this in our equation
\log |2-e^y| + C'= \log|1+x| + C''\\ \log (2-e^y)^{-1}= \log (1+x)+\log C\\ \frac{1}{2-e^y}= C(1+x)

Now, by using boundary conditions we will find the value of C
It is given that y = 0 when x = 0
at x = 0
\frac{1}{2-e^0}= C(1+0)\\ C = \frac{1}{2}
Now, put the value of C
\frac{1}{2-e^y} = \frac{1}{2}(1+x)\\ \\ \frac{2}{1+x}= 2-e^y\\ \frac{2}{1+x}-2= -e^y\\ -\frac{2x-1}{1+x} = -e^y\\ y = \log \frac{2x-1}{1+x}
Therefore, the particular solution is y = \log \frac{2x-1}{1+x}, x\neq-1

Question:15 The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20, 000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?

Answer:

Let n be the population of the village at any time t.

According to question,

\frac{dn}{dt} = kn\ \ (k\ is\ a\ constant)

\\ \implies \int \frac{dn}{n} = \int kdt \\ \implies \log n = kt + C

Now, at t=0, n = 20000 (Year 1999)

\\ \implies \log (20000) = k(0) + C \\ \implies C = \log2 + 4

Again, at t=5, n= 25000 (Year 2004)

\\ \implies \log (25000) = k(5) + \log2 + 4 \\ \implies \log 25 + 3 = 5k + \log2 +4 \\ \implies 5k = \log 25 - \log2 -1 =\log \frac{25}{20} \\ \implies k = \frac{1}{5}\log \frac{5}{4}

Using these values, at t =10 (Year 2009)

\\ \implies \log n = k(10)+ C \\ \implies \log n = \frac{1}{5}\log \frac{5}{4}(10) + \log2 + 4 \\ \implies \log n = \log(\frac{25.2.10000}{16}) = \log(31250) \\ \therefore n = 31250

Therefore, the population of the village in 2009 will be 31250.

Question:16 The general solution of the differential equation \frac{ydx - xdy}{y} = 0 is

(A) xy = C

(B) x = Cy^2

(C) y = Cx

(D) y = Cx^2

Answer:

Given equation is
\frac{ydx - xdy}{y} = 0
we can rewrite it as
dx = \frac{x}{y}dy\\ \frac{dy}{y}=\frac{dx}{x}
Integrate both the sides
we will get
\log |y| = \log |x| + C\\ \log \frac{y}{x} = C \\ \frac{y}{x} = e^C\\ \frac{y}{x} = C\\ y = Cx
Therefore, answer is (C)

Question:17 The general solution of a differential equation of the type \frac{dx}{dy} + P_1 x = Q_1 is

(A) ye^{\int P_1 dy} = \int \left(Q_1 e^{\int P_1 dy} \right )dy +C

(B) ye^{\int P_1 dx} = \int \left(Q_1 e^{\int P_1 dx} \right )dx +C

(C) xe^{\int P_1 dy} = \int \left(Q_1 e^{\int P_1 dy} \right )dy +C

(D) xe^{\int P_1 dx} = \int \left(Q_1 e^{\int P_1 dx} \right )dx +C

Answer:

Given equation is
\frac{dx}{dy} + P_1 x = Q_1
and we know that the general equation of such type of differential equation is

xe^{\int p_1dy} = \int (Q_1e^{\int p_1dy})dy+ C
Therefore, the correct answer is (C)

Question:18 The general solution of the differential equation e^x dy + (y e^x + 2x) dx = 0 is

(A) xe^y + x^2 = C

(B) xe^y + y^2 = C

(C) ye^x + x^2 = C

(D) ye^y + x^2 = C

Answer:

Given equation is
e^x dy + (y e^x + 2x) dx = 0
we can rewrite it as
\frac{dy}{dx}+y=-2xe^{-x}
It is \frac{dy}{dx}+py=Q type of equation where p = 1 \ and \ Q = -2xe^{-x}
Now,
I.F. = e^{\int p dx }= e^{\int 1dx}= e^x
Now, the general solution is
y(I.F.) = \int (Q\times I.F.)dx+C
y(e^x) = \int (-2xe^{-x}\times e^x)dx+C\\ ye^x= \int -2xdx + C\\ ye^x=- x^2 + C\\ ye^x+x^2 = C
Therefore, (C) is the correct answer

More About NCERT Solutions for Class 12 Maths Chapter 9 Miscellaneous Exercise

Eighteen questions for practising the whole chapter are present in the miscellaneous exercise chapter 9 Class 12. All these questions are solved in Class 12 Maths chapter 9 miscellaneous exercise solutions. The Class 12 Maths chapter 9 miscellaneous solutions are given a stepwise manner and can be accessed for free. Students can also download the NCERT solutions for Class 12 Maths chapter 9 miscellaneous exercise using webpage download options available online.

Also Read| Differential Equations Class 12th Notes

Benefits of NCERT Solutions for Class 12 Maths Chapter 9 Miscellaneous Exercise.

  • By going through the Class 12 Maths chapter 9 miscellaneous exercise solutions students can have better exposure to the concepts detailed in the chapter.

  • All the questions in the miscellaneous exercise chapter 9 Class 12 are important and are important from an exam point of view.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Key Features Of NCERT Solutions For Class 12 Chapter 9 Miscellaneous Exercise

  • Comprehensive Coverage: The solutions encompass all the topics covered in miscellaneous exercise class 12 chapter 9, ensuring a thorough understanding of the concepts.
  • Step-by-Step Solutions: In this class 12 chapter 9 maths miscellaneous solutions, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
  • Accuracy and Clarity: Solutions for class 12 maths miscellaneous exercise chapter 9 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
  • Conceptual Clarity: In this class 12 maths ch 9 miscellaneous exercise solutions, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
  • Inclusive Approach: Solutions for class 12 chapter 9 miscellaneous exercise cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
  • Relevance to Curriculum: The solutions for miscellaneous exercise class 12 chapter 9 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What is the number of exercises covered in the chapter Differential Equations?

Seven including the miscellaneous exercise.

2. How many miscellaneous examples are given in the NCERT book?

Five miscellaneous examples are given in the NCERT Class 12 Maths chapter Differential Equations.

3. Give the number of questions covered in the miscellaneous exercise?

18 questions are covered in the miscellaneous exercise of chapter 9 Class 12 NCERT book

4. What number of objective questions are covered in the NCERT solutions for Class 12 Maths chapter 9 miscellaneous exercise?

3 multiple choice questions with 4 options for each are covered in the  Class 12 Maths chapter 9 miscellaneous exercise .

5. What are the main topics covered in the chapter?

The main topics covered in the chapter are order and degree, general and peculiar solutions of differential equations, formation of the differential equation for which general solution is given and a few methods to solve differential equations.

6. What are the topics covered in the first exercise of the chapter?

The first exercise covers the topic order and degree of differential equations

7. What is the topic covered in the last exercise of the chapter?

Solutions to linear differential equations

8. Why do we solve Class 12 Maths chapter 9 miscellaneous solutions?

After completing the chapter students can test their knowledge through miscellaneous exercises since it covers questions from all main topics of the chapter. 

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

View All School Exams

Certifications By Top Providers

Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:17 PM IST :
CBSE Board Exams 2025: Online portal for availing exemptions by CWSN students opens
December 18, 2024 - 02:57 PM IST
Board Exams: States agree to equivalence; no question paper ‘jumbling’ from next year, says PARAKH CEO
December 12, 2024 - 12:44 PM IST
Board Exam Date 2025 Live: CBSE, ICSE, BSEB, MPBSE Class 10, 12 timetable out; Punjab, Rajasthan schedule soon
December 08, 2024 - 10:34 PM IST
CBSE Board Exams 2025: Guidelines issued for Class 10, 12 practicals
December 03, 2024 - 01:11 PM IST
Board Exam Date Sheet 2025 Live: ICSE, ISC, CBSE, MP time table out; BSEB routine soon
November 26, 2024 - 10:18 PM IST
Board exam dates 2025: CBSE, CISCE, UP, MP, Maharashtra, TN time table out; state-wise updates
November 25, 2024 - 08:42 PM IST
Board Exam Date Sheet 2025: CBSE, UPMSP, MPBSE, Class 10, 12 board exam dates out; BSEB, CGBSE schedules soon
November 22, 2024 - 10:04 PM IST

Stay up-to date with CBSE Class 12th News

Back to top