Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 4.3 Class 9 Maths Chapter 4 - Linear Equations in Two Variables

NCERT Solutions for Exercise 4.3 Class 9 Maths Chapter 4 - Linear Equations in Two Variables

Edited By Vishal kumar | Updated on Oct 05, 2023 03:19 PM IST

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables: Exercise 4.3- Download Free PDF

NCERT Solutions for Class 9 Maths Exercise 4.3 introduces the notion of linear equations in two variables, as well as how to graphically solve linear equations. Linear equations in two variables are equations with a wholly unique solution, no solution, or infinitely many solutions of the form ax+by+c=0, in which a, b, and c are real numbers. To identify the set of solutions to the linear equations with two variables, we must first determine the value of the variables. The graphical representations of linear equations in two variables in graphs were the main topic of the NCERT book Class 9 Maths chapter 4 exercise 4.3. The basic strategy to display linear equations on the graph and discover the point of the equation on the graph is the graphical method of solution of linear equations in two variables. (x, y) is the form in which the solution to a system of linear equations is written.

This Story also Contains
  1. NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables: Exercise 4.3- Download Free PDF
  2. NCERT Solutions for Class 9 Maths Chapter 4 – Linear Equations in Two Variables Exercise 4.3
  3. Access Linear Equations In Two Variables Class 9 Maths Chapter 4 Exercise: 4.3
  4. More About NCERT Solutions for Class 9 Maths Exercise 4.3
  5. Benefits of NCERT Solutions for Class 9 Maths Exercise 4.3
  6. Key Features of 9th Class Maths Exercise 4.3 Answers
  7. NCERT Solutions of Class 10 Subject Wise
  8. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 4.3 Class 9 Maths Chapter 4 - Linear Equations in Two Variables
NCERT Solutions for Exercise 4.3 Class 9 Maths Chapter 4 - Linear Equations in Two Variables

NCERT solutions for Class 9 Maths chapter 4 exercise 4.3 include eight questions, four of which are Long Answer Questions, two of which are Short Answer Questions, one of which is a Multiple Choice Question, and the remaining one is the Main Question with five sub-questions. This Class 9 Maths chapter 4 exercise 4.3 thoroughly explains the fundamentals of linear equations in two variables. The following exercises are also included along with NCERT syllabus Class 9 Maths chapter 4 exercise 4.3.

NCERT Solutions for Class 9 Maths Chapter 4 – Linear Equations in Two Variables Exercise 4.3

Download PDF


Access Linear Equations In Two Variables Class 9 Maths Chapter 4 Exercise: 4.3

Q1 (i) Draw the graph of each of the following linear equations in two variables: x + y = 4

Answer:

Given : x + y = 4

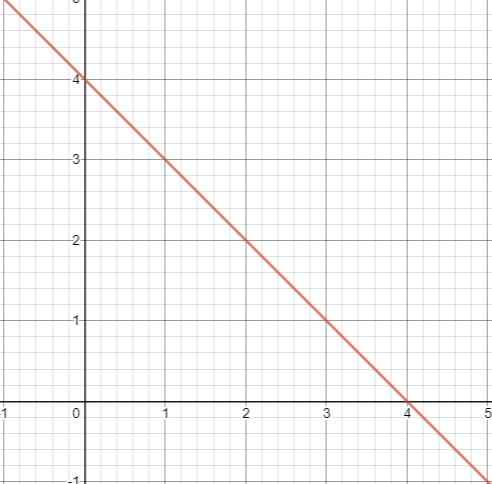
1640075509869

Putting x=0,we have y=4-0=4

Putting x=1,we have y=4-1=3

Thus, (0,4) and (1,3) are solutions of given equation.

Q1 (ii) Draw the graph of each of the following linear equations in two variables: x - y = 2

Answer:

Given : x - y = 2

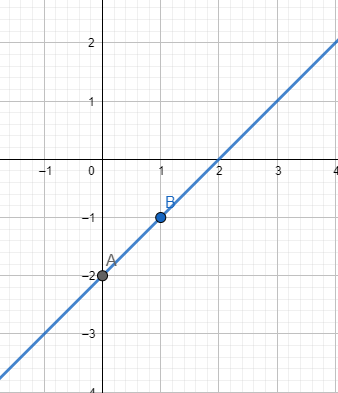
1640075537340

Putting x=0,we have y=0-2=-2

Putting x=1,we have y=1-2=-1

Thus, (0,-2) and (1,-1) are solutions of given equation.

Q1 (iii) Draw the graph of each of the following linear equations in two variables: y = 3x

Answer:

Given : y = 3x

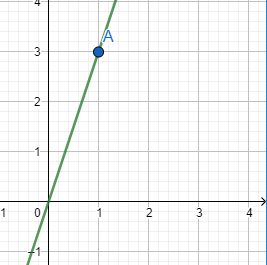
1640075560924

Putting x=0,we have y=3(0)=0

Putting x=1,we have y=3(1)=3

Thus, (0,0) and (1,3) are solutions of given equation.

Q1 (iv) Draw the graph of each of the following linear equations in two variables: 3 = 2x + y

Answer:

Given : 3 = 2x + y

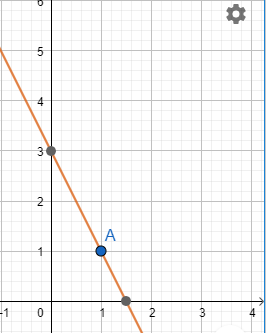
1640075579373

Putting x=0,we have y=3-2.(0)=3

Putting x=1,we have y=3-2.(1)=1

Thus, (0,3) and (1,1) are solutions of given equation.

Q2 Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?

Answer:

The equations of two lines passing through (2, 14) are given by : x+y=16\, \, and\, \, x-y=-12

There are infinite lines passing through (2, 14) because infinite lines pass through a point.

Q3 If the point (3, 4) lies on the graph of the equation 3y = ax+ 7 , find the value of a .

Answer:

Given : the point (3, 4) lies on the graph of the equation 3y = ax+ 7

Put x=3 and y=4

3y = ax+ 7

\Rightarrow 3(4) = a(3)+ 7

\Rightarrow 12 = 3a+ 7

\Rightarrow 12 -7 = 3a

\Rightarrow 5 = 3a

\Rightarrow a=\frac{5}{3}

Q4 The taxi fare in a city is as follows: For the first kilometre, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare as Rs. y, write a linear equation for this information, and draw its graph.

Answer:

Given: The distance covered as x km and total fare is Rs. y.

Total fare =the fare for first km + the fare of the remaining distance

\therefore y=8+5\times (x-1)

\Rightarrow y=8+5x-5

\Rightarrow y=3+5x

For graph,

Putting x=0, we have y=3+5(0)=3

Putting x=1, we have y=3+5(1)=8

Putting x=2, we have y=3+5(2)=13

Hence,(0,3),(1,8) and (2,13) are solutions of equation.

The graph is as shown :

1640075605267

Q5 (A) From the choices given below, choose the equation whose graph is given in Fig. 4.6.

(i) y = x

(ii) x + y = 0

(iii) y = 2x

(iv) 2 + 3 y = 7x

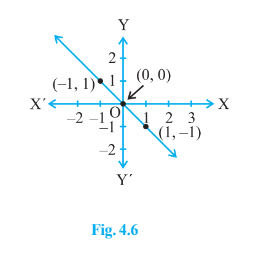
1640075631362

Answer:

For the given figure :

Points on line are (-1,1) , (0,0 ) and (1,-1)

x + y = 0 satisfies all the above points.

Thus, x + y = 0 is the correct equation of the line.

Q5 (B) From the choices given below, choose the equation whose graph is given in Fig. 4.7

(i) y = x + 2

(ii) y = x - 2

(iii) y = -x + 2

(iv) x + 2y = 6


1640075653339

Answer:

For the given figure :

Points on line are (-1,3) , (0,2 ) and (2,0)

y = -x + 2 satisfies all the above points.

Thus, y = -x + 2 is the correct equation of the line.

Q6 (i) If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is: 2 units

Answer:

Let work done be y and distance be x.

Given : Constant force = 5 units

Work done by a body on the application of a constant force is directly proportional to the distance travelled by the body.

i.e. y\, \, \alpha \, \, x

\Rightarrow y=kx

k=Constant force = 5

Then,

\Rightarrow y=5x

For graph,

Put x=0,we have y=5(0)=0

Put x=1,we have y=5(1)=5

Put x=2,we have y=5(2)=10

Points are (0,0) , (0,5) and (2,10)

If the distance travelled is 2 units then the work done is 10 units.

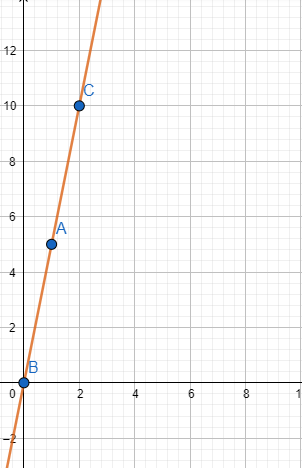
1640075688295

Q6 (ii) If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is : 0 unit

Answer:

Let work done be y and distance be x.

Given : Constant force = 5 units

Work done by a body on the application of a constant force is directly proportional to the distance travelled by the body.

i.e. y\, \, \alpha \, \, x

\Rightarrow y=kx

k=Constant force = 5

Then, \Rightarrow y=5x

For graph,

Put x=0,we have y=5(0)=0

Put x=1,we have y=5(1)=5

Put x=2,we have y=5(2)=10

Points are (0,0) , (0,5) and (2,10)

If the distance travelled is 0 units then work done is 0 units.

Q7 Yamini and Fatima, two students of Class IX of a school, together contributed Rs. 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as Rs. x and Rs. y.) Draw the graph of the same.

Answer:

Let the contribution of Yamini be x.

contribution of Yamini be y.

According to question,

x+y=100

For x=0 , we have y=100-0=100

For x=10 , we have y=100-10=90

For x=20 , we have y=100-20=80

Hence, (0,100) , (10,90) and (20,80)

1640075759528

Q8 (i) In countries like the USA and Canada, the temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius: F = \left(\frac{9}{5} \right )C + 32

Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for the y-axis.

Answer:

Let celsius be on x-axis and Fahrenheit be on y-axis.

F = \left(\frac{9}{5} \right )C + 32

For graph,

Putting x=0, we get y= \left(\frac{9}{5} \right )(0)+ 32=32

Putting x=5, we get y= \left(\frac{9}{5} \right )(5)+ 32=41

Putting x=10, we get y= \left(\frac{9}{5} \right )(10)+ 32=50

Hence, points are (0,32) , (5,41) and (10,50).

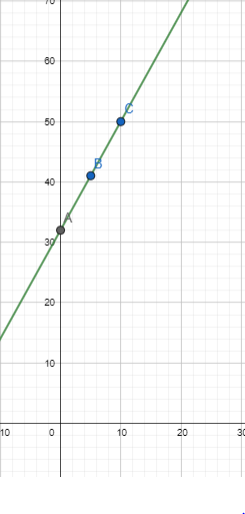
1640077580553

Q8 (ii) In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius: F = \left(\frac{9}{5} \right )C + 32

If the temperature is 30°C, what is the temperature in Fahrenheit?

Answer:

F = \left(\frac{9}{5} \right )C + 32

Put c=30,

F = \left(\frac{9}{5} \right )30 + 32=54+32=86

Thus, the temperature = 30°C, then the temperature is 86 in Fahrenheit.

Q8 (iii) In countries like USA and Canada, the temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius: F = \left(\frac{9}{5} \right )C + 32

If the temperature is 95°F, what is the temperature in Celsius?

Answer:

F = \left(\frac{9}{5} \right )C + 32

Put F=95,

95 = \left(\frac{9}{5} \right )C + 32

\Rightarrow \left(\frac{9}{5} \right )C=95 -32

\Rightarrow \left(\frac{9}{5} \right )C=63

\Rightarrow C=35

If the temperature is 95°F, then 35 is the temperature in Celsius.

Q8 (iv) In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius: F = \left(\frac{9}{5} \right )C + 32

If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?

Answer:

If the temperature is 0°C,

F = \left(\frac{9}{5} \right )C + 32

F = \left(\frac{9}{5} \right )(0) + 32

\Rightarrow F = 32

if the temperature is 0°F,

F = \left(\frac{9}{5} \right )C + 32

0= \left(\frac{9}{5} \right )C + 32

\Rightarrow \left(\frac{9}{5} \right )C=- 32

\Rightarrow C=- 17.8

Thus, if the temperature is 0°C , then the temperature in Fahrenheit is 32 and if the temperature is 0°F, then the temperature in celsius is -17.8.

Q8 (v) In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius: F = \left(\frac{9}{5} \right )C + 32

(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.

Answer:

F = \left(\frac{9}{5} \right )C + 32

Let temperature be x in both Fahrenheit and celsius.

x= \left(\frac{9}{5} \right )x + 32

\Rightarrow 5x= 9x + 160

\Rightarrow 5x-9x = 160

\Rightarrow -4x = 160

\Rightarrow x = -40 \degree

Thus, 40 is the temperature which is numerically the same in both Fahrenheit and celsius.

More About NCERT Solutions for Class 9 Maths Exercise 4.3

A horizontal line and a vertical line divide a Cartesian plane into four areas, with the horizontal line known as the X-axis and the vertical line known as the Y-axis. The origin is also known as the point where both axes meet, and its value is (0, 0) . In Class 9 Maths chapter 4 exercise 4.3, to solve linear equations in two variables graphically, we must first build the graph of the equations by drawing a table for different values of x and y and then display the points on the graph for each equation using the values. Then we'll be able to connect all of the points. As a result, we have the graph. every point on the line satisfies the equation of the line in exercise 4.3 class 9 maths and every solution of the equation is a point on the line.

Also Read| Linear Equations In Two Variables Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Exercise 4.3

• NCERT solutions for Class 9 Maths exercise 4.3 assists us in solving and revising all questions in these exercises, as well as gaining a better understanding of two-variable linear equations.

• If you go through the NCERT solution for Class 9 Maths chapter 4 exercise 4.3, we may gain practice from solving all the questions based on graphical representations of linear equations in two variables and get an overall idea about the topic.

• Exercise 4.3 Class 9 Maths, which is based on graphical representations of linear equations in two variables, will be useful in Class 10 Maths chapter 3 exercise 3.2 - pairs of linear equations with two variables.

Key Features of 9th Class Maths Exercise 4.3 Answers

  1. Expertly Crafted Solutions: The solution for class 9 maths chapter 4 exercise 4.3 have been prepared by subject matter experts. They ensure accuracy and clarity in explanations.

  2. Comprehensive Coverage: Exercise 4.3 class 9 maths covers various topics related to quadratic equations and their solutions. It includes problems involving quadratic equations in one variable.

  3. Step-by-Step Format: Class 9 maths ex 4.3 Solutions are presented in a step-by-step format, making it easy for students to follow the solution process and understand the concepts.

  4. Conceptual Clarity: The primary objective of ex 4.3 class 9 is to help students develop a clear understanding of quadratic equations and their solutions.

  5. Variety of Problems: This Exercise 4.3 class 9 maths offers a range of problems with different levels of complexity, allowing students to practice and enhance their problem-solving skills.

  6. PDF Availability: Solutions are often available in PDF format, allowing students to download and access them offline for convenient studying.

  7. Free of Charge: These resources are typically provided free of charge, making them accessible to all students.

Also see-

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What is the graphical method of solving linear equations in two variables according to NCERT solutions for Class 9 Maths chapter 4 exercise 4.3?

The graphical method of solution of the linear equations is the basic approach to represent the linear equations on the graph and find the point of the given equation.

2. X-coordinate is also called __________

X-coordinate is also called the abscissa 

3. The y-coordinate is also known as ________ .

The y-coordinate is also known as ordinate.

4. Which quadrant is positive?

The positive values of x and y are in quadrant I. Thus quadrant I is known as the positive quadrant.

5. Quadrant 4 is _______

Quadrant 4 is Both positive and negative. Reason: In quadrant 4, the x-coordinates are positive whereas the y-coordinates are negative.

6. Check whether the equation xy-2=7 a linear equation in two variables?

Because the term xy is of degree 2, xy-2=7 is not a two-variable linear equation.

7. Which quadrant does (-7, 8) belong to, according to NCERT solutions for Class 9 Maths chapter 4 exercise 4.3?

 (-7, 8) corresponds to the II quadrants, according to NCERT solutions for Class 9 Maths chapter 4 exercise 4.3.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Karnataka Pre-University Certificate Examination

Exam Date:04 May,2024 - 04 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
Barmer teacher suspended for slapping class 3 student
01/05/2024, 17:07:10
Teacher arrested for `sexual exploitation' at Ujjain Ashram school
01/05/2024, 14:28:18
Delhi NCR schools get bomb threat; fire tender arrives, search underway
01/05/2024, 04:09:04
Education is greatest gift to society: Vice President Jagdeep Dhankhar
30/04/2024, 17:02:12
Jharkhand schools up to Class 8 closed till further orders due to heat wave
30/04/2024, 11:49:37
Delhi School EWS Admission 2024-25: Registration window opens at edudel.nic.in; eligibility
30/04/2024, 09:27:25
Education ministry asks NCERT to review, update textbooks on yearly basis
29/04/2024, 12:22:03
Back to top