Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 3.7 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables

NCERT Solutions for Exercise 3.7 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables

Edited By Ramraj Saini | Updated on Nov 13, 2023 03:31 PM IST | #CBSE Class 10th

NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.7

NCERT Solutions for class 10 maths ex 3.7 Pair of Linear Equations in two variables is discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. This ex 3.7 class 10 includes cross-multiplication, elimination, and substitution methods for solving two-variable linear equations, as well as all of the topics from the whole chapter. A linear equation in two variables is a system of equations of the form ax + by + c = 0, where a, b, c are real numbers, having unique solution, no solutions, or infinitely many solutions. To identify the set of solutions to the linear equations with two variables, there are five mathematical ways including graphical method, replacement method, cross Multiplication method, and elimination method.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.7
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 3 Exercise 3.7
  3. Assess NCERT Solutions for Class 10 Maths chapter 3 exercise 3.7
  4. Pair of Linear Equations in Two Variables Class 10 Chapter 3 Excercise: 3.7
  5. More About NCERT Solutions for Class 10 Maths Exercise 3.7
  6. Benefits of NCERT Solutions for Class 10 Maths Exercise 3.7:
  7. NCERT Solutions of Class 10 Subject Wise
  8. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 3.7 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables
NCERT Solutions for Exercise 3.7 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables

These class 10 maths ex 3.2 solutions are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer! Trusted by 3,500+ universities globally

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 3 Exercise 3.7

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 3 exercise 3.7

Pair of Linear Equations in Two Variables Class 10 Chapter 3 Excercise: 3.7

Q1 The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.

Answer:

Let the age of Ani be a, age of Biju be b ,

Case 1: when Ani is older than Biju

age of Ani's father Dharam:

d=2a and

age of his sister Cathy :

c=\frac{b}{2}

Now According to the question,

a-b=3...........(1)

Also,

\\d-c=30 \\\Rightarrow 2a-\frac{b}{2}=30

\Rightarrow 4a-b=60..............(2)

Now subtracting (1) from (2), we get,

3a=60-3

\Rightarrow a=19

putting this in (1)

19-b=3

\Rightarrow b=16

Hence the age of Ani and Biju is 19 years and 16 years respectively.

Case 2:

b-a=3..........(3)

And

\\d-c=30 \\\Rightarrow 2a-\frac{b}{2}=30

\Rightarrow 4a-b=60..............(4)

Now Adding (3) and (4), we get,

3a=63

\Rightarrow a=21

putting it in (3)

b-21=3

\Rightarrow b=24.

Hence the age of Ani and Biju is 21 years and 24 years respectively.

Q2 One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II]

[Hint : x + 100 = 2(y - 100), y + 10 = 6(x - 10) ]

Answer:

Let the amount of money the first person and the second person having is x and y respectively

Noe, According to the question.

x + 100 = 2(y - 100)

\Rightarrow x - 2y =-300...........(1)

Also

y + 10 = 6(x - 10)

\Rightarrow y - 6x =-70..........(2)

Multiplying (2) by 2 we get,

2y - 12x =-140..........(3)

Now adding (1) and (3), we get

-11x=-140-300

\Rightarrow 11x=440

\Rightarrow x=40

Putting this value in (1)

40-2y=-300

\Rightarrow 2y=340

\Rightarrow y=170

Thus two friends had 40 Rs and 170 Rs respectively.


Q3 A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.

Answer:

Let the speed of the train be v km/h and the time taken by train to travel the given distance be t hours and the distance to travel be d km.

Now As we Know,

speed=\frac{distance }{time}

\Rightarrow v=\frac{d}{t}


\Rightarrow d=vt..........(1)
Now, According to the question,
(v+10)=\frac{d}{t-2}

\Rightarrow (v+10){t-2}=d

\Rightarrow vt +10t-2v-20=d

Now, Using equation (1), we have

\Rightarrow -2v+10t=20............(2)
Also,

(v-10)=\frac{d}{t+3}

\Rightarrow (v-10)({t+3})=d

\Rightarrow vt+3v-10t-30=d
\Rightarrow3v-10t=30..........(3)

Adding equations (2) and (3), we obtain:
v=50.
Substituting the value of x in equation (2), we obtain:
(-2)(50)+10t=20

\Rightarrow -100+10t=20

\Rightarrow 10t=120

\Rightarrow t=12
Putting this value in (1) we get,

d=vt=(50)(12)=600

Hence the distance covered by train is 600km.

Q4 The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.

Answer:

Let the number of rows is x and the number of students in a row is y.
Total number of students in the class = Number of rows * Number of students in a row
=xy

Now, According to the question,

\\xy = (x - 1) (y + 3) \\\Rightarrow xy= xy - y + 3x - 3 \\\Rightarrow 3x - y - 3 = 0 \\ \Rightarrow 3x - y = 3 ...... ... (1)

Also,

\\xy=(x+2)(y-3)\\\Rightarrow xy = xy + 2y - 3x - 6 \\ \Rightarrow 3x - 2y = -6 ... (2)
Subtracting equation (2) from (1), we get:
y=9
Substituting the value of y in equation (1), we obtain:
\\3x - 9 = 3 \\\Rightarrow 3x = 9 + 3 = 12 \\\Rightarrow x = 4
Hence,
The number of rows is 4 and the Number of students in a row is 9.

Total number of students in a class

: xy=(4)(9)=36

Hence there are 36 students in the class.

Q5 In a \Delta\textup{ABC}, \angle C = 3 \angle B = 2( \angle A + \angle B) . Find the three angles.

Answer:

Given,

\angle C = 3 \angle B = 2(\anlge A + \angle B)

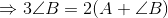
\Rightarrow 3 \angle B = 2(\anlge A + \angle B)

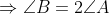
\Rightarrow \angle B = 2 \angle A

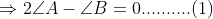
\Rightarrow 2 \angle A -\angle B = 0..........(1)

Also, As we know that the sum of angles of a triangle is 180, so

\angle A +\angle B+ \angle C=180

\angle A +\angle B+ 3\angle B=180^0

\angle A + 4\angle B=180^0..........(2)

Now From (1) we have

\angle B = 2 \angle A.......(3)

Putting this value in (2) we have

\angle A + 4(2\angle A)=180^0.

\Rightarrow 9\angle A=180^0.

\Rightarrow \angle A=20^0.

Putting this in (3)

\angle B = 2 (20)=40^0

And

\angle C = 3 \angle B =3(40)=120^0

Hence three angles of triangles 20^0,40^0\:and\:120^0.

Q6 Draw the graphs of the equations 5x - y =5and 3x - 7 = 3 . Determine the coordinates of the vertices of the triangle formed by these lines and the y-axis.

Answer:

Given two equations,

5x - y =5.........(1)

And

3x - y = 3........(2)

Points(x,y) which satisfies equation (1) are:

X
0
1
5
Y
-5
0
20

Points(x,y) which satisfies equation (1) are:

X
0
1
2
Y
-3
0
3


GRAPH:

Graph

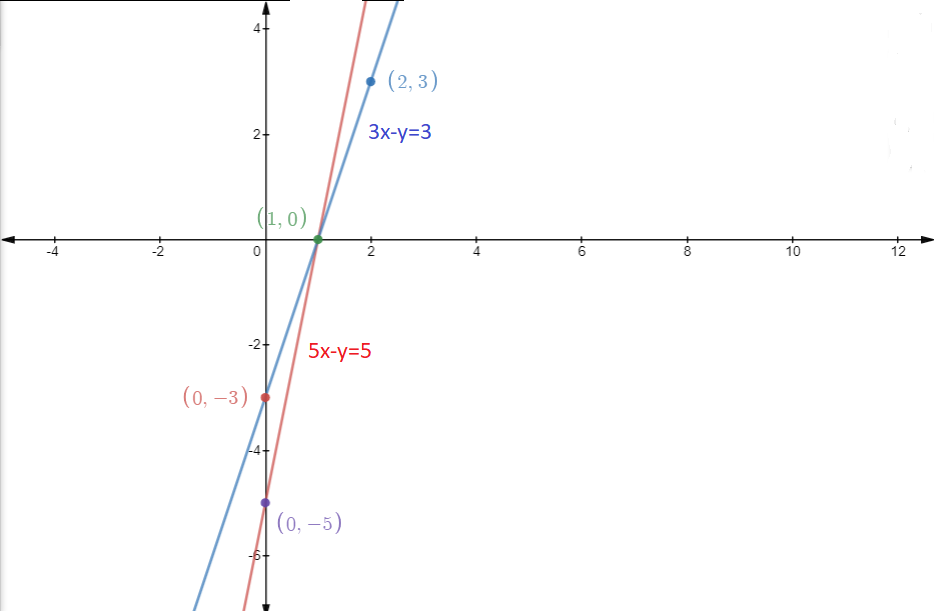
As we can see from the graph, the three points of the triangle are, (0,-3),(0,-5) and (1,0).

Q7 (i) Solve the following pair of linear equations:\\px + qy = p - q\\ qx - py = p + q

Answer:

Given Equations,

\\px + qy = p - q.........(1)\\ qx - py = p + q.........(2)

Now By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(q)(-p-q)-(q-p)(-p)}=\frac{y}{(q-p)(q)-(p)(-p-q)}=\frac{1}{(p)(-p)-(q)(q)}

\frac{x}{-p^2-q^2}=\frac{y}{p^2+q^2}=\frac{1}{-p^2-q^2}

x=1,\:and\:y=-1

Q7 (ii) Solve the following pair of linear equations:\\ax + by = c\\ bx +ay = 1 + c

Answer:

Given two equations,

\\ax + by = c.........(1)\\ bx +ay = 1 + c.........(2)

Now By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(b)(-1-c)-(-c)(a)}=\frac{y}{(-c)(b)-(a)(-1-c)}=\frac{1}{(a)(a)-(b)(b)}

\frac{x}{-b-bc+ac}=\frac{y}{-cb+a+ac}=\frac{1}{a^2-b^2}

x=\frac{-b-bc+ac}{a^2-b^2},\:and\:y=\frac{a-bc+ac}{a^2-b^2}


Q7(iii) Solve the following pair of linear equations: \\\frac{x}{a} - \frac{y}{b} = 0\\ ax + by = a^2 +b^2

Answer:

Given equation,

\\\frac{x}{a} - \frac{y}{b} = 0\\\Rightarrow bx-ay=0...........(1)\\ ax + by = a^2 +b^2...............(2)

Now By Cross multiplication method,

\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{1}{a_1b_2-a_2b_1}

\frac{x}{(-a)(-a^2-b^2)-(b)(0)}=\frac{y}{(0)(a)-(b)(-a^2-b^2)}=\frac{1}{(b)(b)-(-a)(a)}

\frac{x}{a(a^2+b^2)}=\frac{y}{b(a^2+b^2)}=\frac{1}{a^2+b^2}

x=a,\:and\:y=b

Q7(iv) Solve the following pair of linear equations: \\(a-b)x + (a+b)y = a^2 -2ab - b^2\\ (a+b)(x+y) = a^2 +b^2

Answer:

Given,

\\(a-b)x + (a+b)y = a^2 -2ab - b^2..........(1)

And

\\ (a+b)(x+y) = a^2 +b^2\\\Rightarrow (a+b)x+(a+b)y=a^2+b^2...........(2)

Now, Subtracting (1) from (2), we get

(a+b)x-(a-b)x=a^2+b^2-a^2+2ab+b^2

\Rightarrow(a+b-a+b)x=2b^2+2ab

\Rightarrow 2bx=2b(b+2a)

\Rightarrow x=(a+b)

Substituting this in (1), we get,

(a-b)(a+b)+(a+b)y=a^2-2ab-b^2

\Rightarrow a^2-b^2+(a+b)y=a^2-2ab-b^2

\Rightarrow (a+b)y=-2ab

\Rightarrow y=\frac{-2ab}{a+b} .

Hence,

x=(a+b),\:and\:y=\frac{-2ab}{a+b}

Q7(v) Solve the following pair of linear equations: \\152x - 378y = -74\\ -378x + 152y = -604

Answer:

Given Equations,

\\152x - 378y = -74............(1)\\ -378x + 152y = -604............(2)

As we can see by adding and subtracting both equations we can make our equations simple to solve.

So,

Adding (1) and )2) we get,

-226x-226y=-678

\Rightarrow x+y=3...........(3)

Subtracting (2) from (1) we get,

530x-530y=530

\Rightarrow x-y=1...........(4)

Now, Adding (3) and (4) we get,

2x=4

\Rightarrow x=2

Putting this value in (3)

2+y=3

\Rightarrow y=1

Hence,

x=2\:and\:y=1

Q8 ABCD is a cyclic quadrilateral (see Fig. 3.7). Find the angles of the cyclic quadrilateral.

Answer:

As we know that in a quadrilateral the sum of opposite angles is 180 degrees.

So, From Here,

4y+20-4x=180

\Rightarrow 4y-4x=160

\Rightarrow y-x=40............(1)

Also,

3y-5-7x+5=180

\Rightarrow 3y-7x=180........(2)

Multiplying (1) by 3 we get,

\Rightarrow 3y-3x=120........(3)

Now,

Subtracting, (2) from (3) we get,

4x=-60

\Rightarrow x=-15

Substituting this value in (1) we get,

y-(-15)=40

\Rightarrow y=40-15

\Rightarrow y=25

Hence four angles of a quadrilateral are :

\angle A =4y+20=4(25)+20=100+20=120^0

\angle B =3y-5=3(25)-5=75-5=70^0

\angle C =-4x=-4(-15)=60^0

\angle D =-7x+5=-7(-15)+5=105+5=110^0

More About NCERT Solutions for Class 10 Maths Exercise 3.7

NCERT solutions for Class 10 Maths exercise 3.7 covered the graphical approach and algebraic method of linear equations in two variables, types of solutions, and their graphs. At times, two systems of equations can be parallel. In such situations, they have no recourse. The two systems of equations may coincide in exceptional cases, resulting in an infinite number of solutions for the given system. The provided system is said to be consistent since it has a unique solution if the two systems of equations overlap. The following tasks are included along with NCERT book Class 10 Maths chapter 3 exercisr 3.7. All 8 questions are related to the graphical method and algebraic method are given in Exercise 3.7 Class 10 Maths. Also students can get access of Pair of linear equations in two variables notes to revise all the concepts discussed in this chapter.

Benefits of NCERT Solutions for Class 10 Maths Exercise 3.7:

  • NCERT Solutions for Class 10 Maths exercise 3.7 extensively covers a wide range of inquiries identified with every one of the points like cross-multiplication, elimination, and substitution methods.
  • Exercise 3.7 Class 10 Maths, helps the understudies who wish to score high in CBSE Term tests are encouraged to through NCERT solutions for Class 10 Maths exercise 3.7 all through.
  • By tackling the NCERT solution for Class 10 Maths chapter 3 exercise 3.7, students can accomplish a decent score in term tests just as in cutthroat assessments.

Also see-

JEE Main Important Mathematics Formulas

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

Apply

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. According to NCERT solutions for Class 10 Maths chapter 3 exercise 3.7 , What strategies are employed to obtain the solution of a pair of linear equations?

Option 1: 

• Graphical method 

• Algebraic methods 

  • Method of Substitution 

  • Method of Elimination 

  • Method of cross-multiplication

are the approaches used to find the solution to a pair of linear equations 

2. If the pair of linear equations has an infinite number of solutions, then the equations will be _______

If the pair of linear equations have an infinite number of solutions, then the equations will be consistent and dependent. 

3. The pair of equations x=m and y=n graphically represents lines which are

  • Parallel to each other 

  • Intersecting at (n, m)

  • coincident each other

  • Intersecting at (m, n)

The pair of equations x=m and y=n graphically represents lines that are intersecting at (m, n)

 Option (d) intersecting at (m, n)

4. What possibilities exist when two lines intersect in a plane, and what are they?

When two lines are in a plane, there are three alternative solutions. They really are. 

• Two lines may intersect at times. 

• Two lines may not intersect at times, and they may be parallel to each other. 

• Two lines may be coincident at times.

5. Is it important to learn all three methods to solve pairs of linear equations in two variables of NCERT solutions for Class 10 Maths chapter 3 exercise 3.7 ?

Yes, it is important to learn all three methods to solve pairs of linear equations in two variables.

6. What types of questions are covered in the NCERT solutions for Class 10 Maths chapter 3 exercise 3.7 ?

NCERT solutions for Class 10 Maths chapter 3 exercise 3.7 Consists of questions covering topics from the overall chapter that is it has problems related to all the topics like cross-multiplication, elimination, and substitution methods. 

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

National Rural Talent Scholarship Examination

Application Date:05 September,2024 - 20 September,2024

National Institute of Open Schooling 10th examination

Admit Card Date:13 September,2024 - 07 October,2024

National Institute of Open Schooling 12th Examination

Admit Card Date:13 September,2024 - 07 October,2024

Nagaland Board of Secondary Education 12th Examination

Application Date:17 September,2024 - 30 September,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

Hello

The Sadhu Ashram in Aligarh is located in Chhalesar . The ashram is open every day of the week, except for Thursdays . On Mondays, Wednesdays, and Saturdays, it's open from 8:00 a.m. to 7:30 p.m., while on Tuesdays and Fridays, it's open from 7:30 a.m. to 7:30 p.m. and 7:30 a.m. to 6:00 a.m., respectively . Sundays have varying hours from 7:00 a.m. to 8:30 p.m. . You can find it at Chhalesar, Aligarh - 202127 .

Read Complete Answer
vaibhavi bhalsod 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Pearson | PTE
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer! Trusted by 3,500+ universities globally

View All Application Forms
News and Notifications
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST
CBSE conducts surprise inspections at 27 schools in Rajasthan, Delhi to curb menace of dummy schools
September 03, 2024 - 03:02 PM IST
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST
CBSE Class 10 compartment result 2024 soon at cbseresults.nic.in; websites to check
August 03, 2024 - 04:38 PM IST
CBSE 10th, 12th revaluation lot 2 result 2024 out at cbseresults.nic.in; passing marks
July 30, 2024 - 06:39 PM IST

Stay up-to date with CBSE Class 10th News

Back to top