NCERT Class 11 Chemistry Chapter 5 Notes States of Matter - Download PDF
NCERT Class 11 Chemistry chapter 5 notes are based on the different types of forces that exist between the gases. The chapter States of matter Class 11 notes also included the laws that are governed by the gases. Here in this NCERT chapter 5, Class 11 included the laws that are applicable to real and ideal gases.
This Story also Contains
- NCERT Class 11 Chapter 5 Notes
- States of Matter Class 11 Notes- Topic 1:
- Intermolecular Forces:
- States of Matter Class 11 Notes- Topic 2:
- The Gaseous State:
- States of Matter Class 11 Notes- Topic 3:
- Ideal Gas Equation
- States of Matter Class 11 Notes- Topic 4:
- Kinetic Energy and Molecular Speeds:
- States of Matter Class 11 Notes- Topic 5:
- Liquefaction of Gases:
- States of Matter Class 11 Notes- Topic 5:
- Surface Tension:
- NCERT Class 11 Notes Chapter-Wise
Introductory Part may include: The NCERT Class 11 chapter 5 notes gives us a brief intro of Liquification of gases, Viscosity, Surface tension, Vapour pressure, Liquid state. Kinetic energy and molecular speeds, Kinetic molecular theory of gases, Deviation from ideal gas behaviour and the graphs related to it are the highlighting key feature of States of matter 11 Notes. CBSE Class 11 Chemistry chapter 5 notes also cover the basic equations in the chapter. ch 5 chemistry class 11 notes
are important for building basic concepts which further helps chapters like Thermodynamics. The important Laws and their derivations are also covered in the CBSE Class 11 Chemistry chapter 5 notes. All these topics can be downloaded from Class 11 Chemistry chapter 5 notes pdf download. overall cbse class 11 chemistry ch 5 notes are good source for last minute revision.
Also, students can refer,
NCERT Class 11 Chapter 5 Notes
States of Matter Class 11 Notes- Topic 1:
Intermolecular Forces:
The force of attraction and repulsion that exists between particles like atoms and molecules, but does not include any electrostatic forces in between them are intermolecular forces. These forces(attractive) are also known as Van der Waals forces. The variations can be seen in the magnitude of Van der Waals forces and forces included in such category is the dispersion or London forces, Dipole induced dipole forces, and Dipole-dipole forces. A strong type of interaction can be seen in hydrogen bonding only and it is separated from all these forces.
Dispersion forces or London forces:
The London intermolecular force is the temporary and weakest intermolecular force. The force came into existence temporarily when the electrons occupy by the two adjacent atoms. The forces are important to an only short distance where energy is inversely proportional to the sixth power of distance that exists between two particles. Here energy interaction can be seen in the interacting particles and are inversely proportional to r6.
Dipole-Dipole forces:
The forces are formed by the attraction between molecules of one polarised positive end to another polarised negative end. Forces exist between molecules that possess permanent dipoles. The strengths of these forces are lying between 5 kJ to 20 kJ.
For stationary polar molecules, the interaction energy is proportional to r3, but in the case of rotation polar molecules, it is found to be r6.
Dipole induced Dipole forces:
Without any dipole molecule or atom induced dipole on its own. Forces exist between permanent dipoles and molecules with a lack of permanent dipoles. By deforming the electron cloud of an electrically neutral atom, a dipole is induced by another permanent dipole of a polar molecule. In this, the electrical polarizability and permanent polar dipole decide the induced dipoles in the atom. energy interaction can be seen in the interacting particles and are inversely proportional to r6.
Hydrogen Bond:
The species that basically participate in hydrogen bonding is F, O, N and sometimes Cl also. These are used in defining the structure and properties of molecules as they have an energy range between 10 to 100kJmol. The strength of the hydrogen bond can be determined by the bond between the hydrogen of the atom and another electronegative atom. The coulombic interaction exists with hydrogen and other lone pair electrons of the electronegative atom.
States of Matter Class 11 Notes- Topic 2:
The Gaseous State:
Definition Of Gas Constant
The gas constant can be defined as a physical constant and denoted by the letter R. Here R is Regnault constant. This can be found by experimental data of French chemists to calculate the early value of constant. Expressing the molar gas constant which is equivalent to Boltzmann constant and can be expressed in terms of energy per temperature or increment per mole.
Boyle’s Law
By conducting experiments, Robert Boyle came to the conclusion that at a constant temperature, with a fixed amount of pressure , a number of moles of gases varies inversely to that of volume. Such law is Boyle’s Law.
Mathematically it can be represented as follows:
p∝1/V(at constant temperature and moles)
p=k1/V
k1 Used here in this equation is proportionality constant, whose value will depend on gas temperature and units of pressure and volume in which they are expressed.
pV=k1
This denotes that pressure and volume are fixed when the temperature is at a constant condition. Boyle’s equation can also be written as when a fixed amount of gas occupies the volume V1 at a constant temperature at pressure p1 it expands so that volume becomes V2 at a constant temperature of pressure p2,
p1V1=p2V2=constant
Charles’s Law
Defining this law in which pressure remains constant, the volume of a fixed mass of gas is directly proportional to that of absolute temperature
V∝T
V=k2T
VT=constant
Thus, in general, we can write the above equation as follows:
V1T1=V2T2
Gay Lussac’s Law
In this law volume is constant and at fixed pressure conditions the amount of gases may vary directly with temperature. It can be represented as follows:
p∝T
pT=constant=k3
The above equation can also be derived using Charles’s law and Boyle’s Law
Avogadro Law
The law is stated according to the conclusion of Dalton’s atomic theory and Gay Lussac’s law of combining volumes. Such law can be now stated as Avogadro Law.
Defining Avogadro Law as according to temperature and pressure:
An equal volume of all gases contains an equal number of molecules at the same condition where temperature and pressure are the same. In other words, we can write it as under constant pressure and temperature conditions, the volume of gas will depend on the molecules of gases or the amount of gas.
V∝n
V=k4n
n represents the number of moles of gases.
The number of molecules present in one mole of gas is determined using 6.022×1023, which Avogadro constant.
States of Matter Class 11 Notes- Topic 3:
Ideal Gas Equation
An ideal gas can be defined as those gases which obeys the three laws strictly. Such gas is not found in nature and is hypothetical.
Combining all the three equations of above-mentioned laws we conclude:
V∝nTp
V=RnTp…………… (1)
Here R is the constant of proportionality, which is the so-called gas constant.
The value of R is the same for all the gases, so it is also known as the Universal gas constant.
By above expression (1) we obtain
pV=nRT
Gas constant value
The value of gas constant R can be derived from the three laws it can be given as follows:
Gas constant R=8.31445 Jmol-1K-1
The value may differ among units and are used diversely in many disciples.
R constant can be written in the form of Atm; As according to US standard atmosphere the value of R gas constant is given as:
R=8.31445 N.m.kmol-1K-1
Defining Specific Gas Constant
The specific gas constant can be defined as the ratio of the molar mass of gas constant R to the molar mass of a given gas mixture. A specific gas constant can be written as denoted as Rspecific .
Mathematically it can be expressed as:
Rspecific=RM
The specific gas constant in terms of the Boltzmann constant is the same as the Universal gas constant when it is divided by the molecular mass of gas or the mixture of gas. It can be represented as follows:
Rspecific=kbM
The understanding of the universal gas constant is related to calculations of the ideal gas formula and also the other applications of physical science.
States of Matter Class 11 Notes- Topic 4:
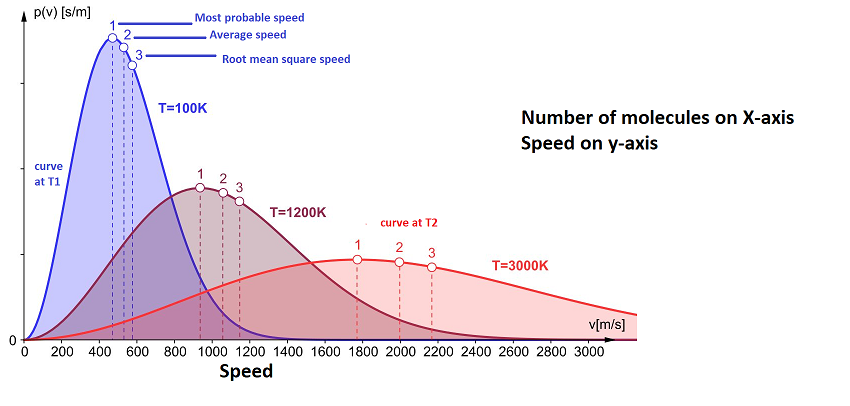
Kinetic Energy and Molecular Speeds:
Showing you the graph which signifies at different temperature ranges the motion of molecules of gases.
A maximum number of speeds can be shown by the peak of the graph and represented symbolically as Ump.
The kinetic energy of the particle can be shown as:
Kinetic energy=1/2mu2
Root mean square speed: This can be defined as the square root of the most probable speeds and the average speed.
urms=√u2
States of Matter Class 11 Notes- Topic 5:
Liquefaction of Gases:
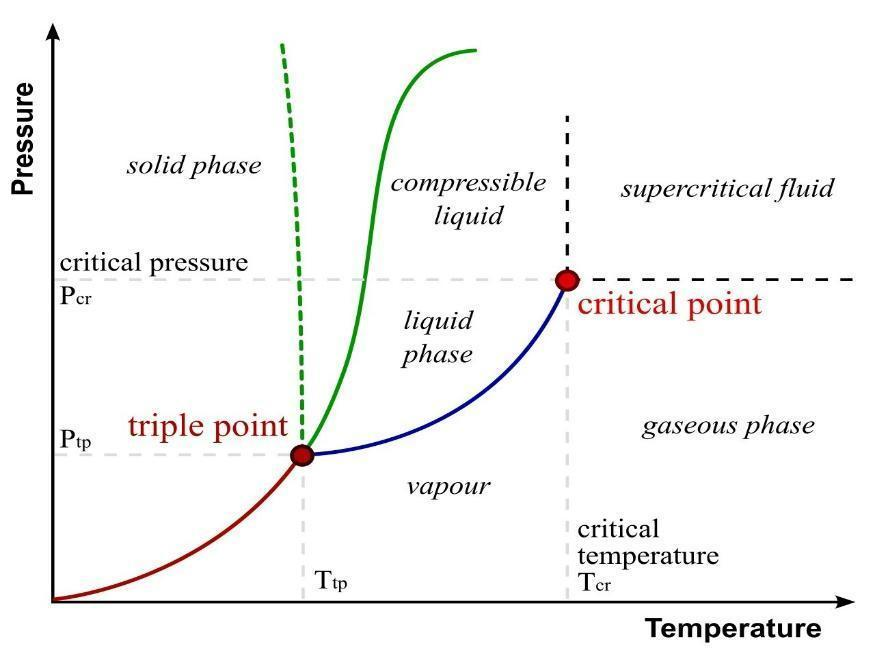
Vapour pressure:
This can be defined as the pressure created in the evacuated chamber by the liquid and exerts pressure on the walls of the chamber. After some time the pressure attains its equilibrium conditions, such pressure is known as vapour pressure and also a condition of equilibrium suggests that this pressure is saturated vapour pressure.
Critical temperature:
The condition arises when the density of liquid and vapours become the same at the point. At that point in time, the clear boundary between liquid and vapour disappears, such temperature is known as critical temperature.
Critical pressure and volume:
This can be defined as the pressure and volume at 1 mole of gas at its critical temperature.
States of Matter Class 11 Notes- Topic 5:
Surface Tension:
The molecule is experiencing force when it is in bulk from all the sides of liquid, rather than experiencing net force. But the molecules that are present on the surface of liquid experience a force inside the liquid called surface tension.
Viscosity: The term viscosity arises in between the layers of liquid, when they slip to one another a frictional force is generated.
Strong intermolecular forces act between the molecules to hold them together and resist the movement.
F∝A
F∝A.dudz ; dudz is velocity gradient
F=μA.dudz
is proportionality constant for coffecient of viscosiy
Significance of NCERT Class 11 Chemistry Chapter 5 Notes
States of matter Class 11 notes, will be helpful in revising the chapter major and minor in a stepwise manner in a very short period of time. The NCERT Class 11 Chemistry chapter 5 notes are designed to cover the needs of each and every student in their doubts with more precision. Also, this NCERT Class 11 Chemistry chapter 5 is important in maintaining the balance between major and minor topics of the Class 11 CBSE Chemistry Syllabus. CBSE Class 11 Chemistry chapter 5 notes include Basic laws of gases which are in turn very important to understand for covering the other chapters in chemistry. Last but not least it is the best guide to score excellent marks in the CBSE board examination. chemistry class 11 chapter 5 notes pdf download can be used to prepare in offline mode. Class 11 States of matter notes contain the laws, different types of forces and also the concept of critical temperature, pressure, viscosity, surface tension. chemistry class 11 chapter 5 notes pdf can be used for revising the concepts just before the exam.
NCERT Class 11 Notes Chapter-Wise
NCERT Class 11 Chemistry Chapter 1 Notes |
NCERT Class 11 Chemistry Chapter 11 Notes |
NCERT Class 11 Chemistry Chapter 12 Notes |
Subject Wise NCERT Exemplar Solutions
- NCERT Exemplar Class 11 Solutions
- NCERT Exemplar Class 11 Maths
- NCERT Exemplar Class 11 Physics
- NCERT Exemplar Class 11 Chemistry
- NCERT Exemplar Class 11 Biology
Subject Wise NCERT Solutions
Frequently Asked Questions (FAQs)
The gas constant can be represented as R and is also known as the universal gas constant. The ideal gas denotes the exact definition of gas constant where the product of pressure to volume is divided by number of moles and temperature of gas and is equal to constant number always. For more details about this topic students can refer to cbse class 11 chemistry ch 5 notes.
Molecules of water are the example of dipole-dipole forces. For more understanding on the topics, students can refer ch 5 chemistry class 11 notes.
The ideal gas constant can be the combination of all the laws:
Boyle’s Law
Charles’s Law
Gay-Lussac’s Law
Avogadro Law or Avogadro number
Ideal gas equation derivation.
Pressure is directly proportional to temperature.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
