NCERT Solutions for Class 11 Maths Chapter 7 Exercise 7.1 - Binomial Theorem
Squares and cubes of binomials like $a+b$ and $a-b$ can be easily evaluated, but what happens when there are higher powers of binomials, like $(a+b)^n$ where the value of n is 8, 9, 10, or even more? So, to overcome this difficulty Binomial Theorem introduces a general formula that makes expansion easier for terms involving higher powers of 'n'
This Story also Contains
- NCERT Solutions Class 11 Maths Chapter 7 Exercise 7.1
- Topics covered in Chapter 7 Binomial Theorem Exercise 7.1
- NCERT Solutions of Class 11 Subject Wise
- Subject-Wise NCERT Exemplar Solutions
In this exercise, Students are going to learn about the Binomial Theorem, Pascal's triangle, and binomial expansion for the positive integers. Solutions of NCERT are designed to provide detailed and step-by-step solutions to every question. Exercise 7.1 solutions are formulated by subject experts in a very clear and comprehensive manner, which helps students to understand concepts easily. Students can also check NCERT Solutions to get detailed solutions for Science and Maths from Class 6 to Class 12.
NCERT Solutions Class 11 Maths Chapter 7 Exercise 7.1
Question 1: Expand the expression. $(1-2x)^5$
Answer:
Given,
The Expression:
$(1-2x)^5$
the expansion of this Expression is,
$(1-2x)^5 =$
$\\^5C_0(1)^5-^5C_1(1)^4(2x)+^5C_2(1)^3(2x)^2-^5C_3(1)^2(2x)^3+^5C_4(1)^1(2x)^4-^5C_5(2x)^5$
$1-5(2x)+10(4x^2)-10(8x^3)+5(16x^4)-(32x^5)$
$1-10x+40x^2-80x^3+80x^4-32x^5$
Question 2: Expand the expression. $\left(\frac{2}{x} - \frac{x}{2} \right )^5$
Answer:
Given,
The Expression:
$\left(\frac{2}{x} - \frac{x}{2} \right )^5$
the expansion of this Expression is,
$\left(\frac{2}{x} - \frac{x}{2} \right )^5\Rightarrow$
$\\^5C_0\left(\frac{2}{x}\right)^5-^5C_1\left(\frac{2}{x}\right)^4\left(\frac{x}{2}\right)+^5C_2\left(\frac{2}{x}\right)^3\left(\frac{x}{2}\right)^2$$-^5C_3\left(\frac{2}{x}\right)^2\left(\frac{x}{2}\right)^3+^5C_4\left(\frac{2}{x}\right)^1\left(\frac{x}{2}\right)^4-^5C_5\left(\frac{x}{2}\right)^5$
$\Rightarrow \frac{32}{x}-5\left ( \frac{16}{x^4} \right )\left ( \frac{x}{2} \right )+10\left ( \frac{8}{x^3} \right )\left ( \frac{x^2}{4} \right )-10\left ( \frac{4}{x^2} \right )\left ( \frac{x^2}{8} \right )$$+5\left ( \frac{2}{x} \right )\left ( \frac{x^4}{16} \right )-\frac{x^5}{32}$
$\Rightarrow \frac{32}{x^5}-\frac{40}{x^3}+\frac{20}{x}-5x+\frac{5x^2}{8}-\frac{x^3}{32}$
Question 3: Expand the expression. $(2x-3)^6$
Answer:
Given,
The Expression:
$(2x-3)^6$
the expansion of this Expression is,
$(2x-3)^6=$
$\Rightarrow$$\\^6C_0(2x)^6-^6C_1(2x)^5(3)+^6C_2(2x)^4(3)^2-^6C_3(2x)^3(3)^3+$$^6C_4(2x)^2(3)^4-^6C_5(2x)(3)^5+^6C_6(3)^6$
$\Rightarrow$$64x^6-6(32x^5)(3)+15(16x^4)(9)-20(8x^3)(27)+15(4x^2)(81)-6(2x)(243)$$+729$
$\Rightarrow$$64x^6-576x^5+2160x^4-4320x^3+4860x^2-2916x+729$
Question 4: Expand the expression. $\left(\frac{x}{3} + \frac{1}{x} \right )^5$
Answer:
Given,
The Expression:
$\left(\frac{x}{3} + \frac{1}{x} \right )^5$
the expansion of this Expression is,
$\left(\frac{x}{3} + \frac{1}{x} \right )^5\Rightarrow$
$\Rightarrow ^5C_0\left(\frac{x}{3}\right)^5+^5C_1\left(\frac{x}{3}\right)^4\left(\frac{1}{x}\right)+^5C_2\left(\frac{x}{3}\right)^3\left(\frac{1}{x}\right)^2$$+^5C_3\left(\frac{x}{3}\right)^2\left(\frac{1}{x}\right)^3+^5C_4\left(\frac{x}{3}\right)^1\left(\frac{1}{x}\right)^4+^5C_5\left(\frac{1}{x}\right)^5$
$\Rightarrow \frac{x^5}{243} +5\left ( \frac{x^4}{81} \right )\left ( \frac{1}{x} \right )+10\left ( \frac{x^3}{27} \right )\left ( \frac{1}{x^2} \right )+10\left ( \frac{x^2}{9} \right )\left ( \frac{1}{x^3} \right )$$+5\left ( \frac{x}{3} \right )\left ( \frac{1}{x^4} \right )+\frac{1}{x^5}$
$\Rightarrow \frac{x^5}{243}+\frac{5x^3}{81}+\frac{10x}{27}+\frac{10}{9x}+\frac{5}{3x^2}+\frac{1}{x^5}$
Question 5: Expand the expression. $\left(x + \frac{1}{x} \right )^6$
Answer:
Given,
The Expression:
$\left(x + \frac{1}{x} \right )^6$
the expansion of this Expression is,
$\left(x + \frac{1}{x} \right )^6$
$\Rightarrow ^6C_0(x)^6+^6C_1(x)^5\left ( \frac{1}{x} \right )+^6C_2(x)^4\left ( \frac{1}{x} \right )^2+^6C_3(x)^3\left ( \frac{1}{x} \right )^3+$$^6C_4(x)^2\left ( \frac{1}{x} \right )^4+^6C_5(x)\left ( \frac{1}{x} \right )^5+^6C_6\left ( \frac{1}{x} \right )^6$
$\Rightarrow x^6+6(x^5)\left ( \frac{1}{x} \right )+15(x^4)\left ( \frac{1}{x^2} \right )+20(8x^3)\left ( \frac{1}{x^3} \right )$$+15(x^2)\left ( \frac{1}{x^4} \right )+6(x)\left ( \frac{1}{x^5} \right )+\frac{1}{x^6}$
$\Rightarrow x^6+6x^4+15x^2+20+\frac{15}{x^2}+\frac{6}{x^4}+\frac{1}{x^6}$
Question 6: Using binomial theorem, evaluate the following:$(96)^3$
Answer:
As 96 can be written as (100-4);
$\\\Rightarrow (96)^3\\=(100-4)^3\\=^3C_0(100)^3-^3C_1(100)^2(4)+^3C_2(100)(4)^2-^3C_3(4)^3$
$\\=(100)^3-3(100)^2(4)+3(100)(4)^2-(4)^3$
$\\=1000000-120000+4800-64$
$\\=884736$
Question 7: Using binomial theorem, evaluate the following:$(102)^5$
Answer:
As we can write 102 in the form 100+2
$\Rightarrow (102)^5$
$=(100+2)^5$
$\\=^5C_0(100)^5+^5C_1(100)^4(2)+^5C_2(100)^3(2)^2$$+^5C_3(100)^2(2)^3+^5C_4(100)^1(2)^4+^5C_5(2)^5$
$=10000000000+1000000000+40000000+800000+8000+32$
$=11040808032$
Question 8: Using binomial theorem, evaluate the following:
Answer:
As we can write 101 in the form 100+1
$\Rightarrow (101)^4$
$=(100+1)^4$
$\\=^4C_0(100)^4+^4C_1(100)^3(1)+^4C_2(100)^2(1)^2$$+^4C_3(100)^1(1)^3+^4C_4(1)^4$
$=100000000+4000000+60000+400+1$
$=104060401$
Question 9: Using binomial theorem, evaluate the following:$(99)^5$
Answer:
As we can write 99 in the form 100-1
$\Rightarrow (99)^5$
$=(100-1)^5$
$\\=^5C_0(100)^5-^5C_1(100)^4(1)+^5C_2(100)^3(1)^2$$-^5C_3(100)^2(1)^3+^5C_4(100)^1(1)^4-^5C_5(1)^5$
$=10000000000-500000000+10000000-100000+500-1$
$=9509900499$
Question 10: Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Answer:
AS we can write 1.1 as 1 + 0.1,
$(1.1)^{10000}=(1+0.1)^{10000}$
$=^{10000}C_0+^{10000}C_1(1.1)+Other \:positive\:terms$
$=1+10000\times1.1+ \:Other\:positive\:term$
$>1000$
Hence,
$(1.1)^{10000}>1000$
Question 11 :Find $(a + b)^4 - (a-b)^4$ . Hence, evaluate$(\sqrt{3} + \sqrt2)^4 - (\sqrt3-\sqrt2)^4$ .
Answer:
Using Binomial Theorem, the expressions $(a+b)^4$ and $(a-b)^4$ can be expressed as
$(a+b)^4=^4C_0a^4+^4C_1a^3b+^4C_2a^2b^2+^4C_3ab^3+^4C_4b^4$
$(a-b)^4=^4C_0a^4-^4C_1a^3b+^4C_2a^2b^2-^4C_3ab^3+^4C_4b^4$
From Here,
$(a+b)^4-(a-b)^4 = ^4C_0a^4+^4C_1a^3b+^4C_2a^2b^2+^4C_3ab^3+^4C_4b^4$$-^4C_0a^4+^4C_1a^3b-^4C_2a^2b^2+^4C_3ab^3-^4C_4b^4$
$(a+b)^4-(a-b)^4 = 2\times( ^4C_1a^3b+^4C_3ab^3)$
$(a+b)^4-(a-b)^4 = 8ab(a^2+b^2)$
Now, Using this, we get
$(\sqrt{3} + \sqrt2)^4 - (\sqrt3-\sqrt2)^4=8(\sqrt{3})(\sqrt{2})(3+2)=8\times\sqrt{6}\times5=40\sqrt{6}$
Question 12 :Find $(x+1)^6 + (x-1)^6$ . Hence or otherwise evaluate $(\sqrt2+1)^6 + (\sqrt2-1)^6$.
Answer:
Using Binomial Theorem, the expressions $(x+1)^4$ and $(x-1)^4$ can be expressed as ,
$(x+1)^6=^6C_0x^6+^6C_1x^51+^6C_2x^41^2+^4C_3x^31^3+^6C_4x^21^4+^6C_5x1^5+^6C_61^6$
$(x-1)^6=^6C_0x^6-^6C_1x^51+^6C_2x^41^2-^4C_3x^31^3+^6C_4x^21^4-^6C_5x1^5+^6C_61^6$
From Here,
$\\(x+1)^6-(x-1)^6=^6C_0x^6+^6C_1x^51+^6C_2x^41^2+^4C_3x^31^3+$$^6C_4x^21^4+^6C_5x1^5+^6C_61^6$$\:\:\:\:\;\:\:\;\:\:\:\ +^6C_0x^6-^6C_1x^51+^6C_2x^41^2-^4C_3x^31^3+^6C_4x^21^4-^6C_5x1^5+^6C_61^6$
$(x+1)^6+(x-1)^6=2(^6C_0x^6+^6C_2x^41^2+^6C_4x^21^4+^6C_61^6)$
$(x+1)^6+(x-1)^6=2(x^6+15x^4+15x^2+1)$
Now, Using this, we get
$(\sqrt2+1)^6 + (\sqrt2-1)^6=2((\sqrt{2})^6+15(\sqrt{2})^4+15(\sqrt{2})^2+1)$
$(\sqrt2+1)^6 + (\sqrt2-1)^6=2(8+60+30+1)=2(99)=198$
Question 13: Show that $9^{n+1} - 8n - 9$is divisible by 64, whenever n is a positive integer.
Answer:
If we want to prove that $9^{n+1} - 8n - 9$is divisible by 64, then we have to prove that $9^{n+1} - 8n - 9=64k$
As we know, from binomial theorem,
$(1+x)^m=^mC_0+^mC_1x+^mC_2x^2+^mC_3x^3+....^mC_mx^m$
Here putting x = 8 and replacing m by n+1, we get,
$9^{n+1}=^{n+1}C_0+\:^{n+1}C_18+^{n+1}C_28^2+.......+^{n+1}C_{n+1}8^{n+1}$
$9^{n+1}=1+8(n+1)+8^2(^{n+1}C_2+\:^{n+1}C_38+^{n+1}C_48^2+.......+^{n+1}C_{n+1}8^{n-1})$
$9^{n+1}=1+8n+8+64(k)$
Now, Using This,
$9^{n+1} - 8n - 9=9+8n+64k-9-8n=64k$
Hence
$9^{n+1} - 8n - 9$ is divisible by 64.
Question 14: Prove that $\sum_{r = 0}^n3^r \ ^nC_r = 4^n$
Answer:
As we know from Binomial Theorem,
$\sum_{r = 0}^na^r \ ^nC_r = (1+a)^n$
Here putting a = 3, we get,
$\sum_{r = 0}^n3^r \ ^nC_r = (1+3)^n$
$\sum_{r = 0}^n3^r \ ^nC_r = 4^n$
Hence Proved.
Also read
Topics covered in Chapter 7 Binomial Theorem Exercise 7.1
The Binomial Theorem for positive integer powers is introduced in this exercise. The formula for the expansion of expressions of the form $(x+a)^n$ is discussed in this exercise.
1) Pascal's Triangle
Pascal's triangle is used to represent the Binomial coefficients. It is a triangular array of numbers, which represents each number is the sum of two numbers directly above it in the previous row.
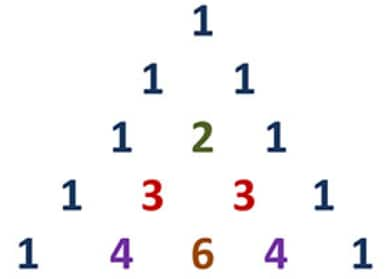
The $n^{\text {th }}$ row of pascal triangle contains $(x+a)^{n-1}$ rows coefficients.
3) Binomial Theorem for any Positive Integer n
The expansion of $(a+b)^n$ is,
$(a+b)^n={ }^n \mathrm{C}_0 a^n+{ }^n \mathrm{C}_1 a^{n-1} b+{ }^n \mathrm{C}_2 a^{n-2} b^2+\ldots+{ }^n \mathrm{C}_{n-1} a \cdot b^{n-1}+{ }^n \mathrm{C}_n b^n$
Binomial Theorem can also be stated as $(a+b)^n=\sum_{k=0}^n{ }^n \mathrm{C}_k a^{n-k} b^k$
Some special cases:
a) Taking $a=x$ and $b=-y$, we obtain
$(x-y)^n=[x+(-y)]^n$
Thus $(x-y)^n={ }^n \mathrm{C}_0 x^n-{ }^n \mathrm{C}_1 x^{n-1} y+{ }^n \mathrm{C}_2 x^{n-2} y^2+\ldots+(-1)^n{ }^n \mathrm{C}_n y^n$
b) Taking $a=1, b=x$, we obtain
$(1+x)^n={ }^n \mathrm{C}_0+{ }^n \mathrm{C}_1 x+{ }^n \mathrm{C}_2 x^2+{ }^n \mathrm{C}_3 x^3+\ldots+{ }^n \mathrm{C}_n x^n$
c) Taking $a=1, b=-x$, we obtain
$(1-x)^n={ }^n \mathrm{C}_0-{ }^n \mathrm{C}_1 x+{ }^n \mathrm{C}_2 x^2-\ldots+(-1)^n{ }^n \mathrm{C}_n x^n$
Also Read
NCERT Solutions of Class 11 Subject Wise
Students can refer subject-wise NCERT solutions. The links to solutions are given below
Subject-Wise NCERT Exemplar Solutions
Students can access the NCERT exemplar solutions to enhance their deep understanding of the topic. These solutions are aligned with the CBSE syllabus and also help in competitive exams.
Frequently Asked Questions (FAQs)
Binomial expansion for positive integers and pascal triangle are covered in the Class 11 Maths exercise 7.1.
Co-ordinate geometry has 10 marks weightage in the CBSE Class 11 Maths exam.
Here you will get NCERT Exemplar Solutions for Class 11 Free.
Yes, NCERT exercise solutions are very helpful for the revision of the important concepts before the exam.
NCERT exercise-wise solutions are prepared by subject matter experts who are experienced in this field.
Yes, NCERT solutions for Class 11 Maths contain the diagrams and charts where ever it is necessary.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
