NCERT Solutions for Class 7 Science Chapter 8 Measurement of Time and Motion
Have you ever asked yourself how we determine the time a pendulum takes to swing or how we determine the speed of a moving car? Class 7 Science Chapter 8 - Measurement of Time and Motion is an answer to that. This chapter discusses the various forms of motion, time measurements and calculation of speed using simple and relatable examples. It aids students in relating real-world observations, such as a car being driven on the road or a ball rolling, to science.
This Story also Contains
- Download Class 7 Science Chapter 8 - Measurement of Time and Motion Question Answers PDF
- Measurement of Time and Motion NCERT Solutions: Exercise Solutions
- Measurement of Time and Motion Class 7 Science Chapter 8: Additional Questions
- Measurement of Time and Motion Class 7 Science Chapter 8: Topics
- Approach to Solve Questions of Class 7 Science Chapter 8 – Measurement of Time and Motion
- Benefits of NCERT Solutions for Class 7 Science Curiosity Chapter 8
- NCERT Solutions for Class 7 Science – Chapter-Wise
.jpg)
The NCERT Solutions for Class 7 Science Chapter 8 - Measurement of Time and Motion give step-wise solutions to all questions set in the textbook, and this way, even the difficult concepts are simple to comprehend. Several critical aspects related to speed, distance-time graphs, time measurement and pendulum clocks are simplified in explanation. The NCERT solutions are made by subject experts according to the latest CBSE syllabus 2025-26 to make sure students do not make some typical errors when converting units and using the formulas. They are useful study guides, whether it is school exams, fast revision, or a strong foundation to competitive exams, since NCERT Solutions for Class 7 Science Chapter 8 - Measurement of Time and Motion provide good guidance. These facilitate self-directed learning, enhance critical thinking and improve self-confidence. Using clear explanations, solved examples, and exam-oriented instructions, Measurement of Time and Motion NCERT Solutions have made the science of motion and time measurement easier than ever before.
Download Class 7 Science Chapter 8 - Measurement of Time and Motion Question Answers PDF
Measurement of Time and Motion class 7 question answers are provided in a simple and downloadable PDF format, which makes the preparation of exams more flexible and efficient. These are step-by-step solutions to all questions of the textbook that include necessary topics like types of motion, methods of measurement of time, distance-time graphs, pendulum clocks, and calculation of speed. By using this free PDF, students have the ability to revise with ease, on their mobile, laptop or tablet, without even having to be connected online. The Measurement of Time and Motion Class 7 question answers, prepared by highly qualified teachers according to the newest NCERT syllabus 2025-26, will allow students to acquire a good conceptual knowledge of the subject, reduce mistakes in unit conversions, and ready the student to take exams. These Class 7 Science Chapter 8 - Measurement of Time and Motion question answers help to revise faster, have a clear understanding of concepts and increase confidence when tackling both textbook problems and exam-based problems.
Measurement of Time and Motion NCERT Solutions: Exercise Solutions
The Measurement of Time and Motion class 7 question answers give a structured solution to all the exercise questions of Chapter 7 of the textbook. These class 7 science chapter 8 Measurement of Time and Motion question answers describe such concepts as types of motion, speed, time measurement, pendulum clocks, and distance-time graphs in plain language so that they are easy to understand. These Measurement of Time and Motion NCERT Solutions are designed based on the most recent NCERT syllabus (2025-26), to ensure that the students are well-prepared to take the exam and have a solid grounding in physics.
Q1. Calculate the speed of a car that travels 150 metres in 10 seconds. Express your answer in km/h.
Answer:
Distance $=150 \mathrm{~m}$
Time taken $=10 \mathrm{~s}$
$
\text { Speed }=\frac{\text { Distance covered }}{\text { Time taken }}=\frac{150 \mathrm{~m}}{10 \mathrm{~s}}
$
Speed in km$/\mathrm{hr}=15 \times \frac{18}{5}=54 \mathrm{~km} / \mathrm{h}$
Q2. A runner completes 400 metres in 50 seconds. Another runner completes the same distance in 45 seconds. Who has a greater speed and by how much?
Answer:
Runner 1:
Distance $=400 \mathrm{~m}$,
Time $=50 \mathrm{~s}$
Speed $=\frac{\text { Distance covered }}{\text { Time taken }}=\frac{400 \mathrm{~m}}{50 \mathrm{~s}}=8 \mathrm{~m} / \mathrm{s}$
Runner 2:
Distance $=400 \mathrm{~m}$,
Time $=50 \mathrm{~s}$
Speed $=\frac{\text { Distance covered }}{\text { Time taken }}=\frac{400 \mathrm{~m}}{45 \mathrm{~s}}=8.89 \mathrm{~m} / \mathrm{s}$
Difference $=8.89-8=0.89 \mathrm{~m} / \mathrm{s}$
Hence, the speed of runner 2 is greater by approximately $0.89 \mathrm{~m} / \mathrm{s}$.
Q3. A train travels at a speed of 25 m/s and covers a distance of 360 km. How much time does it take?
Answer:
$\begin{gathered}\text { Speed }=25 \mathrm{~m} / \mathrm{s} \\ \text { Distance }=360 \mathrm{~km}=3,60,000 \mathrm{~m} \\ \text { Time taken }=\frac{\text { Distance }}{\text { Speed }}=\frac{3,60,0000 \mathrm{~m}}{25 \mathrm{~m} / \mathrm{s}} \\ =14,400 \mathrm{~s} \\ =240 \mathrm{mins} \\ =4 \text { hours }\end{gathered}$
Q4. A train travels 180 km in 3 h. Find its speed in:
(i) km/h
(ii) m/s
(iii) What distance will it travel in 4 h if it maintains the same speed throughout the journey?
Answer:
Distance $=180 \mathrm{~km}$, time $=3 \mathrm{~h}$
(i) Speed $=\frac{\text { Distance }}{\text { Time }}=\frac{180 \mathrm{~km}}{3 \mathrm{~h}_5}=60 \mathrm{~m} / \mathrm{h}$
(ii) Speed in $\mathrm{m} / \mathrm{s}=60 \times \frac{5}{18}=16.677 \mathrm{~m} / \mathrm{s}$
(iii) Time $=4 \mathrm{~h}$, Speed $=60 \mathrm{~km} / \mathrm{h}$
Distance $=$ Speed $\times$ Time
$
=60 \times 4=240 \mathrm{~km}
$
Q5. The fastest galloping horse can reach a speed of approximately 18 m/s. How does this compare to the speed of a train moving at 72 km/h?
Answer:
Speed of horse $=18 \mathrm{~m} / \mathrm{s}$
Speed of train $=72 \mathrm{~km} / \mathrm{h}=72 \times \frac{5}{18}=20 \mathrm{~m} / \mathrm{s}$
The train is faster by $2 \mathrm{~m} / \mathrm{s}$ than the fastest galloping horse.
Q6. Distinguish between uniform and non-uniform motion using the example of a car moving on a straight highway with no traffic and a car moving in city traffic.
Answer:
Uniform motion: If an object covers equal distances in equal distance in equal intervals of time, its motion is said to be uniform. A car moving on a straight highway with no traffic is an example of uniform motion.
Non-uniform motion: If an object covers unequal distances in equal intervals of time, its motion is said to be non-uniform. A car moving in traffic is an example of nonuniform motion.
Q7. Data for an object covering distances in different intervals of time are given in the following table. If the object is in uniform motion, fill in the gaps in the table.
Answer:
In uniform motion, an object covers equal distances in equal intervals of time. Hence, the speed of an object remains constant throughout the motion.
The object covers 8 m every 10 seconds. Hence, the speed of an object remains constant at 0.8 m/s throughout the motion.
Q8. A car covers 60 km in the first hour, 70 km in the second hour, and 50 km in the third hour. Is the motion uniform? Justify your answer. Find the average speed of the car.
Answer:
The car covers different distances in each hour. Hence, the motion of the car is nonuniform.
Total distance $=60 \mathrm{~km}+70 \mathrm{~km}+50 \mathrm{~km}=180 \mathrm{~km}$
Total time $=3$ hours
$
\begin{gathered}
\text { Average speed }=\frac{\text { Total distance travelled }}{\text { Total time taken }} \\
=\frac{180 \mathrm{~km}}{3 \mathrm{~h}}=60 \mathrm{~km} / \mathrm{h}
\end{gathered}
$
Hence, the average speed of the car is $60 \mathrm{~km} / \mathrm{h}$.
Q9. Which type of motion is more common in daily life — uniform or non-uniform? Provide three examples from your experience to support your answer.
Answer:
In our daily life, most motions are nonuniform because objects do not move at the same speed all the time. Their speed changes due to factors like traffic, rough or uneven roads and other obstacles.
Examples:
• Travelling in a bus on an uneven road
• Playing cricket
• Walking through a crowded market
Q10. Data for the motion of an object are given in the following table. State whether the speed of the object is uniform or non-uniform. Find the average speed.
Answer:
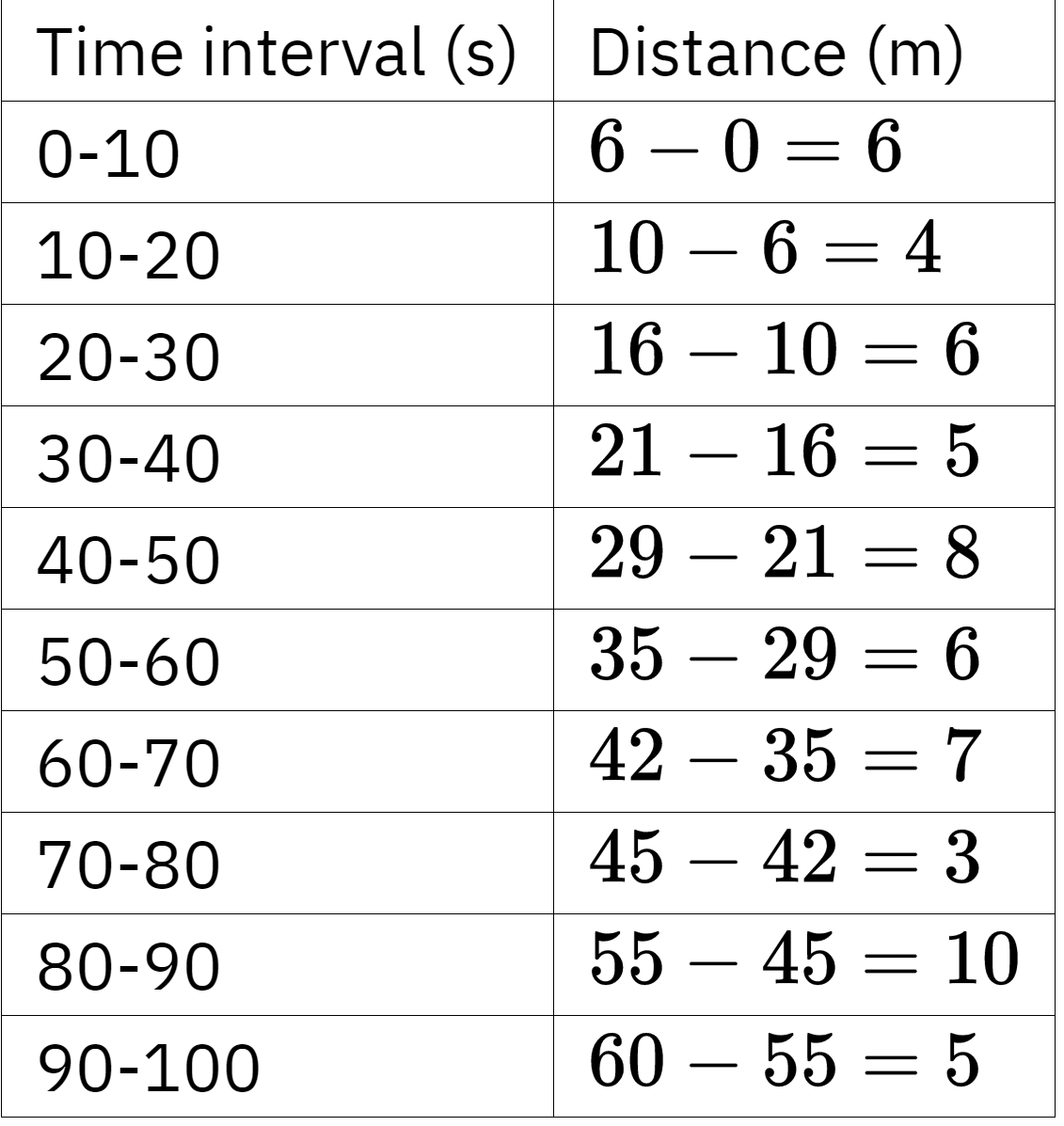
The object exhibits non-uniform motion because it covers
$
\begin{aligned}
& \text { Total distance travelled }=60 \mathrm{~m} \\
& \quad \text { Total time taken }=100 \mathrm{~s} \\
& \text { Average speed }=\frac{\text { Total distance }}{\text { Total time taken }} \\
& \quad=\frac{60}{100} \\
& =0.6 \mathrm{~m} / \mathrm{s}
\end{aligned}
$
Q11. A vehicle moves along a straight line and covers a distance of 2 km. In the first 500 m, it moves with a speed of 10 m/s and in the next 500 m, it moves with a speed of 5 m/s. With what speed should it move the remaining distance so that the journey is complete in 200 s? What is the average speed of the vehicle for the entire journey?
Answer:
Given
Total distance $=2 \mathrm{~km}=2000 \mathrm{~m}$,
Total time $=200$
Step 1: Time taken to cover the first 500 m
$
\text { Time }=\frac{\text { Distance }}{\text { Speed }}=\frac{500}{10}=50 \mathrm{~s}
$
Step 2: Time taken to cover the next 500 m
$
\text { Time }=\frac{500}{10}=100 \mathrm{~s}
$
Step 3: Remaining distance $=2000-1000=1000 \mathrm{~m}$
Remaining time $=200-150=50 \mathrm{~s}$
Step 4: Speed required to cover the remaining 1000 m
$
\text { Speed }=\frac{1000}{50}=20 \mathrm{~m} / \mathrm{s}
$
Step 5: Average speed $=\frac{\text { Totaldistance }}{\text { Totaltimetaken }}=\frac{2000}{200}=10 \mathrm{~m} / \mathrm{s}$
Measurement of Time and Motion Class 7 Science Chapter 8: Additional Questions
Class 7 science Chapter 8 Additional Questions are aimed at helping the students reinforce their knowledge on the measurement of time and motion in real life. Such questions allow doing more work than the textbook exercises, giving students an opportunity to think and use the concepts in reality. Through these questions, students would also develop better problem-solving skills and be able to prepare well for exams.
Q1: Distance between Bholu’s and Golu’s house is 9 km. Bholu has to attend Golu’s birthday party at 7 o’clock. He started from his home at 6 o’clock on his bicycle and covered a distance of 6 km in 40 minutes. At that point he met Chintu and he spoke to him for 5 minutes and reached Golu’s birthday party at 7 o’clock. With what speed did he cover the second part of the journey? Calculate his average speed for the entire journey.
Answer;
Distance between Bholu's and Golu's house $=9 \mathrm{~km}$
Distance covered by Bholu in the first part of the journey $=6 \mathrm{~km}$
Time taken to cover $6 \mathrm{~km}=40 \mathrm{~min}$
Distance covered by Bholu in second part of the journey $=9-6=3 \mathrm{~km}$
Time taken to cover $3 \mathrm{~km}=60-(40+5)=15 \mathrm{~min}$
The speed of Bholu while covering the second part of the journey
$
\begin{aligned}
& =\frac{3 \mathrm{~km}}{\left(\frac{15}{60}\right) \mathrm{h}} \\
& =12 \mathrm{~km} / \mathrm{h}
\end{aligned}
$
Average speed of Bholu for the entire journey
$
\begin{aligned}
& =\frac{\text { Total distance }}{\text { Time taken }} \\
& =\frac{9 \mathrm{~km}}{60 \mathrm{~min}} \\
& =9 \mathrm{~km} / \mathrm{h}
\end{aligned}
$
Q2: Boojho goes to the football ground to play football. The distance-time graph of his journey from his home to the ground is given in the figure below
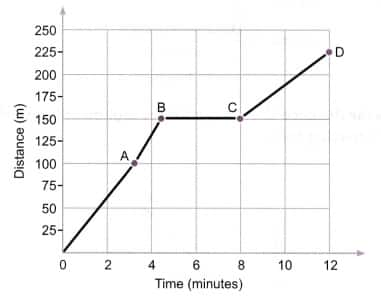
(a) What does the graph between points B and C indicate about the motion of Boojho?
(b) Is the motion between 0 to 4 minutes uniform or nonuniform?
(c) What is his speed between 8 and 12 minutes of his journey?
Answer:
a. Graph between points B and C is a horizontal line, which indicates that Boojho is at rest, i.e., his speed is zero.
b. Motion between 0 to 4 minutes is non-uniform as the distance-time graph for this time interval is not a straight line.
c. Speed of Boojho between 8 and 12 minutes of his journey
$
\begin{aligned}
& =\frac{(225-150) \mathrm{m}}{(12-8) \mathrm{min}} \\
& =\frac{75}{4} \\
& =18.75 \mathrm{~m} / \mathrm{min}
\end{aligned}
$
Q3: The average age of children of Class VII is 12 years and 3 months. Express this age in seconds.
Answer:
The average age $=12$ years 3 months
1 year $=365$ Days
$=365 \times 24$ hours $[\because 1$ days $=24$ hours $]$
$=365 \times 24 \times 3600 \mathrm{sec}[\because 1$ hour $=3600 \mathrm{sec}]=31536000 \mathrm{sec}$
So, 12 years $=31536000 \mathrm{sec} \times 12=378432000$ seconds
And 3 months $=3 \times 30$ days $=3 \times 30 \times 24$ hours $=3 \times 30 \times 24 \times 3600$ s $=77$
Now, the total age in seconds $=378432000 \mathrm{~s}+7776000 \mathrm{~s}=386208000 \mathrm{~s}$
Measurement of Time and Motion Class 7 Science Chapter 8: Topics
The Class 7 Science Chapter 8 - Measurement of Time and Motion provides a student with an exciting introduction to the world of measuring motion and time as a key to comprehending it. This chapter describes significant scientific tools, techniques, and concepts that are applied in our daily lives to determine speed, distance, and time. It assists students in establishing a good grounding in physics by connecting real-life illustrations, such as moving vehicles and moving clocks, with the scientific concept of motion and measurement.
8.1 Measurement of Time
8.1.1 A simple pendulum
8.1.2 SI unit of time
8.2 Slow or Fast
8.3 Speed
8.4 Uniform and Non-uniform Linear Motion
Approach to Solve Questions of Class 7 Science Chapter 8 – Measurement of Time and Motion
The chapter Measurement of Time and Motion assists the students to comprehend the recognition of motion, its measurement, and calculation using such concepts as speed, distance, and time. In order to effectively answer questions in this chapter, one should pay attention to conceptual clarity and logical use. Here's a useful approach:
- Grasp the Basics: Get to know the meaning of distance, displacement, speed and time. Know the relation with each other by mere formulas.
- Relate to Real-Life Illustrations: Use the motion in everyday life--as cars on the roads, or a swinging pendulum, or a racehorse. This facilitates easier remembrance of the concepts.
- Learn to Work with Units and Conversions: Take extra care in units (m, km, s, hr) and conversions, because it is here that mistakes are frequently made.
- Use Diagrams and Graphs: Solve distance-time graphs and use pendulum diagrams. Drawing increases the strength of explanations and the acquisition of more marks.
- Practice Formula-Based Problems: Solve problems of speed, time and distance step by step. It is always best to write the formula first and then replace values.
- Learn Through Activities: Experience basic phenomena like the pendulum of a clock or measure the time of an object in motion to develop useful knowledge about motion and time measurement.
- Revise Key Terms: Review concepts such as uniform motion, oscillation, simple pendulum, speed, average speed, and distance-time graph to be able to answer correctly.
- Solve NCERT Exercises and Extra Questions: Practice both textual and application-based questions to strengthen exam readiness and avoid common mistakes.
Benefits of NCERT Solutions for Class 7 Science Curiosity Chapter 8
The NCERT Solutions of Class 7 Science Chapter 8 - Measurement of Time and Motion are used to help students grasp the main scientific concepts concerning motion, speed, and time in a proper way. These class 7 science chapter 8 Measurement of Time and Motion question answers provide step-by-step solutions to textbook questions, which allow students to understand concepts and enhance their skills in solving problems. They are structured based on the newest NCERT syllabus and reinforce conceptual understanding, and help to prepare effectively to take exams based on straightforward explanations and real-life examples.
1. Clearly Defined Concepts
Measurement of Time and Motion class 7 question answers offer clear and sequential descriptions of such concepts as speed, time, distance, periodic and non-periodic motion and normal units.
2. Proper Use of Formulae & Units
Students are taught how to work with formulas (such as Speed = Distance/Time) correctly, learn the concept of SI units, conversion formula and computing techniques that are used to solve numerical questions.
3. Boosts Calculation and Problem-Solving Skills
The detailed solution of numerical problems and reasoning question papers enhances the mathematical and analytical skills of students. Solutions provide ways in which students interpret and solve tables or diagrams in motion graphs and questions.
4. Helps in Exam Preparation
Model answers reflect current NCERT question trends, which equip students to deal with all kinds of exam questions, objective, short answer, long answer, and HOTS (Higher Order Thinking Skills).
NCERT Solutions for Class 7 Science – Chapter-Wise
The NCERT Solutions of Class 7 Science give step-by-step solutions of all the chapters of the new NCERT textbook. These solutions assist students in developing a good foundation, planning well before exams, and comprehending concepts easily. It is easy to revise or access any topic with the chapter-wise links, making it easier to learn and more organised.
NCERT Solutions for Class 7- Subject Wise
Also Check NCERT Books and NCERT Syllabus here
Also Check NCERT Books and NCERT Syllabus here
Frequently Asked Questions (FAQs)
Q: What are the benefits of using the NCERT Solutions for Class 7 Science Chapter 8 to develop analytical skills?
A:
By working through problems that require calculations and graphs:
1. Students become better at using logic.
2. They improve their interpretation of data
3. They boost precision while selecting units or methods
Q: How can students be ready for the Class 7 Science Chapter 8 exam questions using the NCERT Solution approach?
A:
Solutions offer:
- Detailed solutions that are in line with the CBSE
- Practice with graphs and equations.
- Definitions and unit clarification
- Discussion about the often asked questions and mistakes
Q: What topics are included in the NCERT curriculum Class 7 Science?
A:
The NCERT curriculum Class 7 Science covers various chapters such as nutrition, heat transfer, plant reproduction, motion, and electric current, with exercises and activities to make learning interactive.
Q: Where can I study from the Science textbook for Class 7 NCERT?
A:
You can follow the Science textbook for Class 7 NCERT which is designed according to the CBSE syllabus and covers all important scientific concepts in simple language with examples.
Q: Is the swing in the playground an example of periodic movement?
A:
Yes, a swing moves back and forth on a regular basis and is a type of periodic motion, just like a simple pendulum
Q: Does the weight of an object play a role in how fast it moves?
A:
Not really. Speed is mainly dependent upon the force applied to the object and the surface it is travelling on. A heavy object might travel slower if not enough force is applied.
Q: What are some devices that measure time?
A:
Some devices we can use to measure time are clocks, watches, stopwatches, sundials, water clocks, and sand timers.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters