NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions - Download PDF

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions - Download PDF

Edited By Ravindra Pindel | Updated on Feb 07, 2024 06:13 PM IST

NCERT Solutions for algebraic expressions class 7: An algebraic expression contains variables, numbers, and operations. In this article, you will get NCERT solutions for class 7 maths chapter 12 Algebraic Expressions. All the algebraic expressions are explained in NCERT. In solutions of NCERT for Class 7 Maths chapter 12 Algebraic Expressions, you will get questions related to solving all three types of algebraic expressions. Also, you will learn the addition and subtraction of algebraic expression. There are many problems in the CBSE NCERT solutions for Class 7 Maths chapter 12 Algebraic Expressions which will give more clarity of the concepts. You can also refer to the NCERT syllabus of Class 7 Maths for better understanding. Check NCERT Solutions from Classes 6 to 12 for Science and Math by clicking on the above link. Here you will get NCERT Solutions for Class 7 for Maths Chapter 12 .

Latest: NCERT Class 7 Maths: Chapterwise Important Formulas with Examples and Points

This Story also Contains

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions - Important Formulae
NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7 - Important Points
NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7
NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7th Topic 12.2
NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Topic 12.3
NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7th Topic 12.4
NCERT Solutions for Class 7th Math Chapter 12 Algebraic Expressions Topic 12.5 Monomials, Binomials, Trinomials and Polynomials
NCERT Solutions for Class 7th Math Chapter 12 Algebraic Expression Exercise 12.1
NCERT Solutions for Class 7th Math Chapter 12 Algebraic Expressions Topic 12.6
NCERT Solutions for Chapter 12 Maths Class 7 Algebraic Expression Exercise: 12.2
NCERT Solutions for Chapter 12 Maths Class 7th Algebraic Expression Exercise 12.3
NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expression Exercise 12.4
Algebraic Expressions Class 7 Chapter 12-Topics

This chapter is important for our coming classes. We must practice questions of this chapter and must be able to solve problems very fastly.

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions - Important Formulae

Perimeter of Equilateral triangle = 3a, where, a = side length of triangle

Perimeter of a square = 4a, where, a = side length of square

Perimeter of regular pentagon = 5a, where, a = side length of pentagon

Area of square = a², where, a = side length of square

Area of rectangle = l × b where, l = length and b = breadth

Area of a Triangle = (1/2) ( b) (h), where b = base and h = height

NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7 - Important Points

Variable: A symbol denoted by letters (such as x, y, z, p, q, r, etc.) that can vary, representing an unknown quantity or value.

How Are Expressions Formed:

Algebraic expressions are formed by combining variables and constants using mathematical operations (Addition, Subtraction, Multiplication, Division).

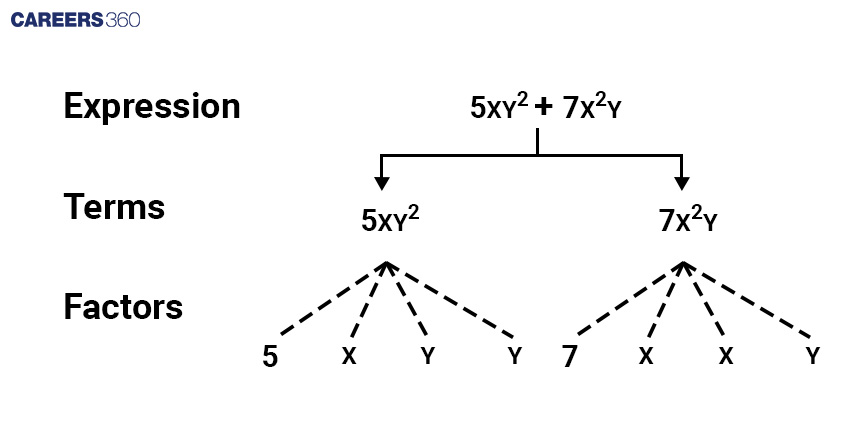
Terms and Factors of An Expression:

Terms are components of expressions formed by combining variables and constants.

The term includes the sign, so we say "added" without specifying addition or subtraction.

In the diagram, factors are shown with dotted lines and terms with continuous lines.

1692070816523

Coefficient: The coefficient is the numerical factor of a term in an expression.

Free download NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions PDF for CBSE Exam.

NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7

NCERT Solutions for Class 7 Maths Chapter 12 Questions and Exercise

NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7th Topic 12.2

Question: Describe how the following expressions are obtained:

$7xy+5, x^{2} y,4x^{2}-5x$

Answer: $7xy+5$

the above expression is obtained by adding 7xy with 5. Here 7xy is obtained by multiplying 7,x and y

$4 x^2-5x$

the above expression is obtained by subtracting the product of 5 and x from the product of 4,x and x

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Topic 12.3

Question:1 What are the terms in the following expressions? Show how the terms are formed. Draw a tree diagram for each expression:

$8y+3x^{2},7mn-4,2x^{2}y.$

Answer: $8y+3x^{2}$ The terms in the expression are

$8y\ and\ 3x^{2}$

$8y+3x^{2}$ is obtained by adding the product of 8 and y with the product of 3 x and x

the tree diagram for the expression is given below

1643021027441

$7mn-4$ has two terms 7mn and 4 and the expression is obtained by subtracting 4 from the product of 7,m and n. The tree diagram is shown below.

$2x^2y$ has only one term, that is the expression itself.

The expression is formed by multiplying 4 terms 2, x, x and y. The tree diagrams are shown below

1643021048526

Question:2 Write three expressions each having 4 terms.

Answer: We can write as many expressions we need with 4 terms. Following are a few examples of expression with 4 terms

$\\ a+b+c+d\\ab+bc+cd+ad\\abc+bcd+acd+abcd$

Question: Identify the coefficients of the terms of following expressions:

$4x-3y,a+b+5,2y+5,2xy$

Answer: i) $4x-3y$ has two terms 4x and -3y

the coefficient of x is 4 and the coefficient of y is -3

ii) a+b+5 has 3 terms a,b and a constant that is 5.

the coefficient of a is 1 and b is also 1. Constant terms have no coefficient

iii) 2y+5 has two terms 2y and 5 which is constant.

The coefficient of y is 2. Constant terms have no coefficient

iv) 2xy has only one term which is 2xy and the coefficient of xy is 2

NCERT Solutions for Maths Chapter 12 Algebraic Expressions Class 7th Topic 12.4

Question:1(i) Group the like terms together from the following:

$12x$ , $12$ , $-25x$ , $-25$ , $-25y$ , $1$ , $x$ , $12y$ , $y$

Answer: The like terms are grouped below

Group 1: $12x$ , $-25x$ , $x$

Group 2: $-25y$ , $12y$ , $y$

Group 3: $12$ , $-25$ , $1$

NCERT Solutions for Class 7th Math Chapter 12 Algebraic Expressions Topic 12.5 Monomials, Binomials, Trinomials and Polynomials

Question: Classify the following expressions as a monomial, a binomial or a trinomial:

$a,a+b.ab+a+b,ab+a+b-5,xy,xy+5,5x^{2}-x+2,4pq-3q+5p,7,4m-7n+10,4mn+7.$

Answer: Monomial: a, xy, 7

binomial: a+b, xy+5, 4mn+7

Trinomial: ab+a+b, 5x ² -x+2, 4pq-3q+5p, 4m-7n+10

Polynomial with 4 terms: ab+a+b-5

NCERT Solutions for Class 7th Math Chapter 12 Algebraic Expression Exercise 12.1

Question: 1(i) Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

Subtraction of $z$ from $y$ .

Answer: Subtraction of z from y: $y-z$

Question: 1(ii) Get the algebraic expressions in the following cases using variables, constants and arithmetic operation.

One-half of the sum of numbers $x$ and $y$ .

Answer: Sum of numbers x and y = x + y

One half of the sum of numbers x and y

$=\frac{x+y}{2}$

Question: 1(iii) Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

The number $z$ multiplied by itself.

Answer:

The number $z$ multiplied by itself $=z\times z=z^{2}$

Question: 1(iv) Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

One-fourth of the product of numbers $p$ and $q$ .

Answer: Product of the numbers p and q $= p \times q=pq$

One-fourth of the product of numbers p and q

$=\frac{pq}{4}$

Question: 1(v) Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

Numbers $x$ and $y$ both squared and added.

Answer: Number x squared = $x^{2}$

Number y squared = $y^{2}$

Numbers x and y both squared and added = $x^{2}+ y^{2}$

Question:1(vi) Get the algebraic expressions in the following cases using variables, constants and arithmetic operation.

Number 5 added to three times the product of numbers $m$ and $n$ .

Answer: Product of numbers m and n $=m\times n=mn$

Number 5 added to three times the product of numbers $m$ and $n$ = $=3\times mn+5=3mn+5$

Question:1(vii) Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

Product of numbers $y$ and $z$ subtracted from $10$ .

Answer: Product of numbers y and z $=y\times z=yz$

Product of numbers y and z subtracted from 10 $=10-yz$

Question: 1(viii) Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.

Sum of numbers $a$ and $b$ subtracted from their product.

Answer: Sum of numbers a and b = a + b

Product of the numbers a and b $=a\times b=ab$

Sum of numbers $a$ and $b$ subtracted from their product $= ab - (a+b) = ab - a - b$ .

Question:2(i) Identify the terms and their factors in the following expressions

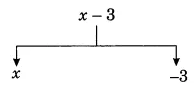
Show the terms and factors by tree diagrams. (a) $x-3$

Answer: Expression : x - 3

Terms in the above expression: x and -3

Tree diagram for the given expression

1643021082718

Question: 2 (i) Identify the terms and their factors in the following expressions

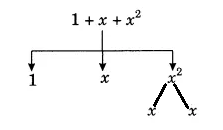
Show the terms and factors by tree diagrams (b) $1+x+x^{2}$

Answer: Expression: $1 + x + x^2$

Tems in the above expression: $1, x \and\ x^2$

Factors of x ² : x and x

Tree diagram for the given expression

1643021117870

Question:2(i) Identify the terms and their factors in the following expressions

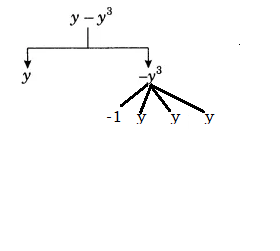
Show the terms and factors by tree diagrams (c) $y-y^{3}$

Answer: Expression: y - y ³

Terms in the above expression: y and -y ³

Factors of -y ³ : -1, y, y and y

Tree diagram for the given expression

1643021160195

Question: 2 (i) Identify the terms and their factors in the following expressions

Show the terms and factors by tree diagrams. (d) $5xy^{2}+7x^{2}y$

Answer: Expression: 5xy ² + 7x ² y

Terms in the above expression: 5xy ² and 7x ² y

Factors of 5xy ² : 5, x, y and y

Factors of 7x ² y: 7, x, x and y

Tree diagram for the given expression

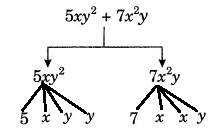
1643021192704

Question: 2 (i) Identify the terms and their factors in the following expressions

Show the terms and factors by tree diagrams (e) $-ab+2ab^{2}-3a^{2}$

Answer:

Expression: -ab + 2ab ² - 3a ²

Terms in the above expression: -ab, 2ab ² and -3a ²

Factors of -ab: -1, a and b

Factors of 2ab ² : 2, a, b and b

Factors of -3a ² : -1, 3, a and a

Tree diagram for the given expression

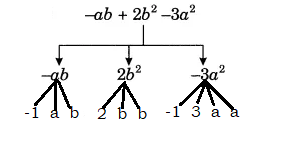
1643021223439

Question: 2 (ii) Identify terms and factors in the expressions given below:

(a) $-4x+5$

Answer: Expression: -4x + 5

Terms in the above expression: -4x and 5

Factors of -4x: -1, 4 and x

Factors of 5: 5

Question: 2 (ii) Identify terms and factors in the expressions given below:

(b) $-4x+5y$

Answer: Expression: -4x + 5y

Terms in the above expression: -4x and 5y

Factors of -4x: -1, 4 and x

Factors of 5y: 5 and y

Question: 2 (ii) Identify terms and factors in the expressions given below:

(c) $5y+3y^{2}$

Answer: Expression: 5y + 3y ²

Terms in the above expression: 5y and 3y ²

Factors of 5y: 5 and y

Factors of 3y ² : 3, y and y

Question: 2 (ii) Identify terms and factors in the expressions given below:

(d) $xy+2x^{2}y^{2}$

Answer: Expression: xy + 2x ² y ²

Terms in the above expression: xy and 2x ² y ²

Factors of xy: x and y

Factors of 2x ² y ² : 2, x, x, y and y

Question: 2 (ii) Identify terms and factors in the expressions given below:

(e) $pq+q$

Answer: Expression: pq + q

Tems in the above expression: pq and q

Factors of pq: p and q

Factors of q: q

Question: 2 (ii) Identify terms and factors in the expressions given below:

(f) $1.2 \; ab-2.4\; b+3.6\; a$

Answer: Expression: 1.2ab - 2.4b + 3.6a

Tems in the above expression: 1.2ab, -2.4b and 3.6a

Factors of 1.2ab: 1.2, a and b

Factors of -2.4b: -1, 2.4 and b

Factors of 3.6a: 3.6 and a

Question: 2( ii) Identify terms and factors in the expressions given below:

(g) $\frac{3}{4}x+\frac{1}{4}$

Answer: Expression: $\frac{3}{4}x+\frac{1}{4}$

Terms in the above expression: $\frac{3}{4}x$ and $\frac{1}{4}$

Factors of $\frac{3}{4}x$ : $\frac{3}{4}$ and x

Factors of $\frac{1}{4}$ : $\frac{1}{4}$

Question: 2 (ii) Identify terms and factors in the expressions given below:

(h) $0.1\; p^{2}+0.2\; q^{2}$

Answer: Expression: 0.1p ² + 0.2q ²

Tems in the above expression:0.1p ² and 0.2q ²

Factors of 0.1p ² : 0.1, p and p

Factors of 0.2q ² : 0.2, q and q

Question:3(i) Identify the numerical coefficients of terms (other than constants) in the following expressions:

Answer: Expression: 5 - 3t ²

Tems in the above expression: 5 and -3t ²

Coefficient of -3t ² : -3

Question:3(ii) Identify the numerical coefficients of terms (other than constants) in the following expressions:

$1+t+t^{2}+t^{3}$

Answer: Expression: 1 + t + t ² + t ³

Terms in the above expression: 1, t, t ² and t ³

Coefficient of t is 1

Coefficient of t ² is 1

Coefficient of t ³ : is 1

Question: 3(iii) Identify the numerical coefficients of terms (other than constants) in the following expressions:

Answer: Expression: x + 2xy + 3y

Terms in the above expression: x, 2xy and 3y

Coefficient of x: 1

Coefficient of 2xy: 2

Coefficient of 3y: 3

Question: 3(iv) Identify the numerical coefficients of terms (other than constants) in the following expressions:

Answer: Expression: 100m + 1000n

Terms in the above expression: 100m and 1000n

Coefficient of 100m: 100

Coefficient of 1000n: 1000

Question: 3(v) Identify the numerical coefficients of terms (other than constants) in the following expressions:

$-p^{2}q^{2}+7pq$

Answer: Expression: -p ² q ² + 7pq

Tems in the above expression: -p ² q ² and 7pq

Coefficient of -p ² q ² : -1

Coefficient of 7pq: 7

Question:3(vi) Identify the numerical coefficients of terms (other than constants) in the following expressions:

$1.2\; a+0.8\; b$

Answer: Expression: 1.2a + 0.8b

Terms in the above expression: 1.2a and 0.8b

Coefficient of 1.2a: 1.2

Coefficient of 0.8b: 0.8

Question:3(vii) Identify the numerical coefficients of terms (other than constants) in the following expressions:

Answer: Expression: 3.14r ²

Terms in the above expression: 3.14r ²

Coefficient of 3.14r ² is 3.1

Question: 3(viii) Identify the numerical coefficients of terms (other than constants) in the following expressions:

Answer: Expression: 2(l + b) = 2l + 2b

Tems in the above expression: 2l and 2b

Coefficient of 2l: 2

Coefficient of 2b: 2

Question: 3(ix) Identify the numerical coefficients of terms (other than constants) in the following expressions:

$0.1\; y+0.01\; y^{2}$

Answer: Expression: 0.1y + 0.01y ²

Tems in the above expression: 0.1y and 0.01y ²

Coefficient of 0.1y is 0.1

Coefficient of 0.01y ² is 0.01

Question: 4 (a) Identify terms which contain x and give the coefficient of x.

(i) $y^{2}x+y$

Answer: Expression: y ² x + y

Terms with x: y ² x

Coefficient of x in y ² x: y ²

Question:4(a) Identify terms which contain x and give the coefficient of x.

(ii) $13y^{2}-8yx$

Answer: Expression: 13y ² - 8yx

Terms with x: -8yx

Coefficient of x in -8yx: -8y

Question: 4 (a) Identify terms which contain x and give the coefficient of x.

(iii) $x+y+2$

Answer: Expression: x + y + 2

Terms with x: x

Coefficient of x in x: 1

Question: 4 (a) Identify terms which contain x and give the coefficient of x.

(iv) $5+z+zx$

Answer: Expression: 5 + z + zx

Terms with x: zx

Coefficient of x in zx: z

Question: 4 (a) Identify terms which contain x and give the coefficient of x .

(v) $1+x+xy$

Answer: Expression: 1 + x + xy

Terms with x: x and xy

Coefficient of x in x: 1

Coefficient of x in xy: y

Question:4(a) Identify terms which contain x and give the coefficient of x.

(vi) $12xy^{2}+25$

Answer: Expression: 12xy ² + 5

Terms with x: 12xy ²

Coefficient of x in 12xy ² : 12y ²

Question:4(a) Identify terms which contain x and give the coefficient of x.

(vii) $7x+xy^{2}$

Answer: Expression: 7x + xy ²

Terms with x: 7x and xy ²

Coefficient of x in 7x: 7

Coefficient of x in xy ² : y ²

Question: 4 (b) Identify terms which contain $y^{2}$ and give the coefficient of $y^{2}$ .

Answer: Expression: 8 - xy ²

Terms with y ² : -xy ²

Coefficient of y ² in -xy ² : -x

Question: 4 (b) Identify terms which contain $y^{2}$ and give the coefficient of $y^{2}$ .

(ii) $5y^{2}+7x$

Answer: Expression: 5y ² + 7x

Terms with y ² : 5y ²

Coefficient of y ² in 5y ² : 5

Question: 4 (b) Identify terms which contain $y^{2}$ and give the coefficient of $y^{2}$ .

(iii) $2x^{2}y-15xy^{2}+7y^{2}$

Answer: Expression: 2x ² y -15xy ² + 7y ²

Terms with y ² : -15xy ² and 7y ²

Coefficient of y ² in -15xy ² : -15x

Coefficient of y ² in 7y ² : 7

Question:5 Classify into monomials, binomials and trinomials.

(i) 4y – 7z

(ii) y ²

(iii) x + y – xy

(iv) 100

(v) ab – a – b

(vi) 5 – 3t

(vii) 4p ² q – 4pq ²

(viii) 7mn

(ix) z ² – 3z + 8

(x) a ² + b ²

(xi) z ² + z

(xii) 1 + x + x ²

Answer: (i) 4y – 7z

Binomial

(ii) y ²

Monomial

(iii) x + y – xy

Trinomial

(iv) 100

Monomial

(v) ab – a – b

Trinomial

(vi) 5 – 3t

Binomial

(vii) 4p ² q – 4pq ²

Binomial

(viii) 7mn

Monomial

(ix) z ² – 3z + 8

Trinomial

(x) a ² + b ²

Binomial

(xi) z ² + z

Binomial

(xii) 1 + x + x ²

Trinomial

Question:6(i) State whether a given pair of terms is of like or unlike terms.

Answer: (i) $1,100$ are Like terms.

Question:6(ii) State whether a given pair of terms is of like or unlike terms.

$-7x,\frac{5}{2}x$

Answer: (ii) $-7x,\frac{5}{2}x$ are Like terms

Question:6(iii) State whether a given pair of terms is of like or unlike terms.

Answer: Unlike since y and x are unlike terms

Question: 6(iv) State whether a given pair of terms is of like or unlike terms.

Answer: Like terms, since both the terms contain xy and only the coefficient is different

Question: 6(v) State whether a given pair of terms is of like or unlike terms.

$4m^{2}p,4mp^{2}$

Answer: Unlike since $m^2p \ and \ mp^2$ are different

Question: 6(vi) State whether a given pair of terms is of like or unlike terms.

$12xz,12x^{2}z^{2}$

Answer: Unlike since $xz \ and\ x^2z$ are unlike terms

Question:7(a) Identify like terms in the following:

$-xy^{2},-4yx^{2},8x^{2},2xy^{2},7y,-11x^{2},-100x,-11yx,20x^{2}y,-6x^{2},y,2xy,3x$

Answer: Like terms are

(i) -xy ² and 2xy ²

(ii) -4x ² y and 20x ² y

(iii) 8x ² , -11x ² and -6x ²

(iv) 7y and y

(v) -100x and 3x

(vi) -11yx and 2xy

Question:7(b) Identify like terms in the following:

$10pq,7p,8q,-p^{2}q^{2},-7qp,-100q,-23,12q^{2}p^{2},-5p^{2},41,2405p,78qp,13p^{2}q,qp^{2},701p^{2}$

Answer: Like terms are

(i) 10pq, -7qp and 78qp

(ii) 7p and 2405p

(iii) 8q and -100q

(iv) -p ² q ² and 12q ² p ²

(vii) -23 and 41

(viii) -5p ² and 701p ²

(ix) 13p ² q and qp ²

NCERT Solutions for Class 7th Math Chapter 12 Algebraic Expressions Topic 12.6

Question:(i) Add and subtract

Answer: Adding

$m-n,m+n$

Will give the result as follows

$m-n+m+n=2m$

Subtracting

$m-n,m+n$

Will give the result as follows

$m-n-(m+n)=m-n-m-n=-2n$

Question:(ii) Add and subtract

Answer: Adding the following terms

$mn+5-2,mn+3$

we will get

$mn+5-2+mn+3=2mn+6$

Subtracting

$mn+5-2,mn+3$

We will get

$mn+5-2-(mn+3)=mn+5-2-mn-3=0$

NCERT Solutions for Chapter 12 Maths Class 7 Algebraic Expression Exercise: 12.2

Question: 1(i) Simplify combining like terms:

$21b-32+7b-20b$

Answer: 21b - 32 + 7b -20b

= (21 + 7 - 20)b -32

= 8b - 32

The simplified expression is 8b - 32.

Question:1(ii) Simplify combining like terms:

$-z^{2}+13z^{2}-5z+7z^{3}-15z$

Answer: $-z^{2}+13z^{2}-5z+7z^{3}-15z$

-z ² + 13z ² - 5z + 7z ³ - 15z

= (-1 + 13)z ² + (-5 - 15)z +7z ³

=12z ² - 20z + 7z ³

The simplified expression is 12z ² - 20z + 7z ³

Question:1(iii) Simplify combining like terms:

$p-(p-q)-q-(q-p)$

Answer: p - (p - q) - q - (q - p)

= p - p + q - q - q + p

= p - p + p + q - q -q

= p - q

The simplified expression is p - q.

Question: 1(iv) Simplify combining like terms:

$3a-2b-ab-(a-b+ab)+3ab+b-a$

Answer: 3a - 2b - ab - (a - b + ab) + 3ab + b - a

= 3a - 2b - ab - a + b - ab + 3ab + b - a

= (3 - 1 - 1)a + (-2 + 1 +1)b + (-1 - 1 + 3)ab

= a + ab

The simplified expression is a + ab.

Question:1(v) Simplify combining like terms:

$5x^{2}y-5x^{2}+3yx^{2}-3y^{2}+x^{2}-y^{2}+8xy^{2}-3y^{2}$

Answer: 5x ² y - 5x ² + 3yx ² - 3y ² + x ² - y ² + 8xy ² - 3y ²

= (5 + 3 )x ² y + (-5 + 1)x ² + (-3 - 1 - 3)y ² + 8xy ²

= 8x ² y - 4x ² - 7y ² + 8xy ²

The simplified expression is 8x ² y - 4x ² - 7y ² + 8xy ²

Question:1(vi) Simplify combining like terms:

$(3y^{2}+5y-4)-(8y-y^{2}-4)$

Answer: (3y ² + 5y - 4) - (8y - y ² - 4)

= 3y ² + 5y - 4 - 8y + y ² + 4

= (3 + 1)y ² + (5 - 8)y - 4 + 4

= 4y ² - 3y

The simplified expression is 4y ² - 3y

Question:2 Add:

(i) $3mn,-5mn,8mn,-4mn$

(ii) $t-8tz,3tz-z,z-t$

(iii) $-7mn+5,12mn+2,9mn-8,-2mn-3$

(iv) $a+b-3,b-a+3,a-b+3$

(v) $14x+10y-12xy-13,18-7x-10y+8xy,4xy$

(vi) $5m-7n,3n-4m+2,2m-3mn-5$

(vii) $4x^{2}y,-3xy^{2},-5xy^{2},5x^{2}y$

(viii) $3p^{2}q^{2}-4pq+5,-10 p^{2}q^{2},15+9pq+7p^{2}q^{2}$

(ix) $ab-4a,4b-ab,4a-4b$

(x) $x^{2}-y^{2}-1,y^{2}-1-x^{2},1-x^{2}-y^{2}$

Answer: The given terms are added as follows

$\\(i) 3mn + (-5mn) + 8mn + (-4mn)\\ = (3 - 5 + 8 - 4)mn\\ = 2mn$

$\\(ii) t - 8tz + (3tz - z) + (z - t)\\ = t - 8tz + 3tz - z + z - t\\ = (1 - 1)t + (-8 + 3)tz + (-1 + 1)z\\ = -5tz$

$\\(iii) -7mn + 5 + (12mn + 2) + (9mn - 8) + (-2mn - 3)\\ = -7mn + 5 + 12mn + 2 + 9mn - 8 - 2mn - 3 \\= (-7 + 12 + 9 - 2)mn + 5 + 2 - 8 - 3 \\= 12mn - 4$

$\\(iv) a + b - 3 + (b - a + 3) + (a - b + 3)\\ \\= a + b - 3 + b - a + 3 + a - b + 3 \\= (1 - 1 + 1)a + (1 + 1 -1)b - 3 + 3 + 3 \\= a + b + 3$

$\\(v) 14x + 10y - 12xy - 13 + (18 - 7x - 10y + 8xy) + 4xy\\ = 14x + 10y - 12xy - 13 + 18 - 7x - 10y + 8xy + 4xy \\= (14 -7)x + (10 - 10)y + (-12 + 8 + 4)xy - 13 + 18 \\= 7x + 5$

$\\(vi) 5m - 7n + (3n - 4m + 2) + (2m - 3mn - 5) \\= 5m - 7n + 3n - 4m + 2 + 2m - 3mn - 5 \\= (5 - 4 + 2)m + (-7 + 3)n + 2 - 5 - 3mn \\= 3m - 4n - 3mn - 3$

$\\(viii) 3p^2q^2 - 4pq + 5 + (-10p^2q^2) + (15 + 9pq + 7p^2q^2) \\= 3p^2q^2 - 4pq + 5 - 10p^2q^2 + 15 + 9pq + 7p^2q^2 \\= (3 - 10 + 7)p^2q^2 + (-4 + 9)pq + 5 + 15 \\= 5pq + 20$

$\\(ix) ab - 4a + (4b - ab) + (4a - 4b) \\= ab - 4a + 4b - ab + 4a - 4b \\= (1 - 1)ab + (-4 + 4)a + (4 - 4)b \\=0$

$\\(x)\ x^2 - y^2 - 1 + (y^2 - 1 - x^2) + (1 - x^2 - y^2) \\= (1 - 1 - 1)x^2 + (-1 + 1 - 1)y^2 - 1 - 1 + 1 \\= -x^2 - y^2 - 1$

Question:3 Subtract:

(i) $-5y^{2}$ from $y^{2}$

(ii) $6xy$ from $-12xy$

(iii) $(a-b)$ from $(a+b)$

(iv) $a(b-5)$ from $b(5-a)$

(v) $-m^{2}+5mn$ from $4m^{2}-3mn+8$

(vi) $-x^{2}+10x-5$ from $5x-10$

(vii) $5a^{2}-7ab+5b^{2}$ from $3ab-2a^{2}-2b^{2}$

(viii) $4pq-5q^{2}-3p^{2}$ from $5p^{2}+3q^{2}-pq$

Answer: The given terms are subtracted as follows

(i)

$\\ y^2 - (-5y^2) \\= y^2 + 5y^2 \\= 6y^2$

(ii)

$\\ -12xy - 6xy\\ = -18xy$

(iii)

$\\(a+b)-(a-b)\\ =a+b-a+b =2b$

(iv)

$\\ b(5 - a) - a(b - 5) \\= 5b - ab - (ab - 5a) \\= 5b - ab - ab + 5a \\= 5b - 2ab + 5a$

(v)

$\\4m^2 - 3mn + 8 - (-m^2 + 5mn) \\= 4m^2 - 3mn + 8 + m^2 - 5mn \\= (4 + 1)m^2 + (-3 - 5)mn + 8 \\= 5m^2 - 8mn + 8$

(vi)

$\\ 5x - 10 - (-x^2 + 10x - 5) \\= 5x - 10 + x^2 - 10x + 5 \\= x^2 + (5 - 10)x - 10 + 5 \\= x^2 - 5x - 5$

(vii)

$\\ 3ab - 2a^2 - 2b^2 - (5a^2 - 7ab + 5b^2) \\= 3ab - 2a^2 - 2b^2 - 5a^2 + 7ab - 5b^2 \\= (3 + 7)ab + (-2 -5)a^2 + (-2 - 5)b^2 \\= 10ab - 7a^2 - 7b^2$
(viii)

$\\ 5p^2 + 3q^2 - pq - (4pq - 5q^2 - 3p^2) \\= 5p^2 + 3q^2 - pq - 4pq + 5q^2 + 3p^2 \\= (5 + 3) p^2 + (3 + 5)q^2 + (-1 - 4)pq \\= 8p^2 + 8q^2 - 5pq$

Question: 4 (a) What should be added to $x^{2}+xy+y^{2}$ to obtain

Answer: Let the term be a which must be added to x ² + xy + y ² to obtain 2x ² + 3xy

$\\a + x^2 + xy + y^2 = 2x^2 + 3xy \\a = 2x^2 + 3xy - (x^2 + xy + y^2) \\a = (2-1)x^2 + (3 - 1)xy -y^2 \\a = x^2 + 2xy - y^2$

x ² + 2xy - y ² should be added to x ² + xy + y ² to obtain 2x ² + 3xy

Question: 4 (b) What should be subtracted from $2a+8b+10$ to get

Answer: Let the term be c which must be subtracted from 2a + 8b + 10 to get -3a + 7b + 16

$\\2a + 8b + 10 - c = -3a + 7b + 16 \\c = 2a + 8b + 10 - (-3a + 7b + 16) \\c = 2a + 8b + 10 + 3a - 7b - 16 \\c = (2 + 3)a + (8 - 7)b + 10 - 16 \\c = 5a + b - 6$

5a + b - 6 must be subtracted from 2a + 8b + 10 to get -3a + 7b + 16

Question: 5 What should be taken away from $3x^{2}-4y^{2}+5xy+20$ to obtain

$-x^{2}-y^{2}+6xy+20 ?$

Answer: Let the term be a which must be taken away from 3x ² - 4y ² + 5xy + 20 to obtain -x ² - y ² + 6xy + 20

$\\3x^2 - 4y^2 + 5xy + 20 - a = -x^2 - y^2 + 6xy + 20 \\a = 3x^2 - 4y^2 + 5xy + 20 - ( -x^2 - y^2 + 6xy + 20 ) \\a = 3x^2 - 4y^2 + 5xy + 20 + x^2 + y^2 - 6xy - 20 \\a = ( 3 + 1 )x^2 + ( -4 + 1 )y^2 + ( 5 - 6 )xy + 20 - 20 \\a = 4x^2 - 3y^2 - xy$

4x ² - 3y ² - xy must be taken away from 3x ² - 4y ² + 5xy + 20 to obtain -x ² - y ² + 6xy + 20

Question:6(a) From the sum of $3x-y+11$ and $-y-11$ , subtract $3x-y-11.$

Answer:

$\\( 3x - y + 11 + ( - y - 11 ) ) - ( 3x - y - 11 ) \\= 3x - y + 11 - y - 11 - 3x + y + 11 \\= ( 3 - 3 )x + ( -1 - 1 + 1)y + 11 - 11 + 11 \\= -y + 11$

On subtracting 3x - y - 11 from the sum of 3x - y + 11 and -y - 11 we get -y + 11

Question: 6 (b) From the sum of $4+3x$ and $5-4x+2x^{2},$ subtract the sum of $3x^{2}-5x$ and $-x^{2}+2x+5$ .

Answer:

$\\( 4 + 3x + ( 5 - 4x + 2x^2) ) - ( 3x^2 - 5x + ( -x^2 + 2x + 5) \\= (4 + 3x + 5 - 4x + 2x^2 ) - ( 3x^2 - 5x -x2 + 2x + 5) \\= 4 + 3x + 5 - 4x + 2x^2 - 3x^2 + 5x + x^2 - 2x - 5 \\=4 + 5 - 5 + ( 3 - 4 + 5 - 2 )x + ( 2 - 3 + 1 )x^2 \\=4 + 2x$

On subtracting the sum of $3x^{2}-5x$ and $-x^{2}+2x+5$ from the sum of $4+3x$ and $5-4x+2x^{2}$ we get $4+2x$

NCERT Solutions for Chapter 12 Maths Class 7th Algebraic Expression Exercise 12.3

Question:1(i) If $m=2,$ find the value of:

Answer: (i) m - 2

= 2 - 2

= 0

If m = 2 the value of m - 2 = 0

Question:1(ii) If $m=2,$ find the value of:

Answer:

$\\3m - 5 \\= 3 \times 2 - 5 \\= 6 - 5 \\= 1$

If m = 2 the value of 3m - 5 = 1

Question:1(iii) If $m=2,$ find the value of:

Answer:

$\\9 - 5m \\= 9 - 5 \times 2 \\= 9 - 10 \\= -1$

If m = 2 the value of 9 - 5m = -1

Question: 1(iv) If $m=2,$ find the value of:

Answer:

$\\3m^2 - 2m - 7 \\= 3 \times 2^2 - 2 \times 2 - 7 \\= 12 - 4 - 7 \\= 1$

If m = 2 the value of 3m ² - 2m - 7 = 1

Question: 1(v) If find the value of: (v) If $m=2,$ find the value of:

$\frac{5m}{2}-4$

Answer:

$\frac{5m}{2}-4$

$=\frac{5\times 2}{2}-4$

= 5 - 4

= 1

If m = 2 the value of $\frac{5m}{2}-4 = 1$

Question:2(i) If $p=-2,$ find the value of:

Answer:

$\\4p + 7 \\= 4 \times ( -2 ) + 7 \\= -8 + 7 \\= -1$

If p = -2 the value of 4p + 7 = -1

Question: 2(ii) If $p=-2,$ find the value of:

Answer:

$\\-3p^2 + 4p + 7 \\= -3 x ( -2 )^2 + 4 x ( -2 ) + 7 \\= -12 - 8 + 7 \\= -13$

If p = -2 the value of -3p ² + 4p + 7 = -13

Question: 2(iii) If $p=-2$ , find the value of:

$-2p^{3}-3p^{2}+4p+7$

Answer:

$\\-2p3 - 3p2 + 4p + 7 \\= - 2 \times ( -2)^3 - 3 \times ( -2 )^2 + 4 \times ( -2 ) + 7 \\= 16 - 12 - 8 + 7 \\= 3$

If p = -2 the value of -2p ³ - 3p ² + 4p + 7 = 3

Question: 3(i) Find the value of the following expressions, when $x=-1$ :

Answer:

$\\2x - 7 \\= 2 \times ( -1 ) - 7 \\= -2 - 7 \\= -9$

If x = -1 the value of 2x - 7 = -9

Question: 3(ii) Find the value of the following expressions, when

Answer:

-x + 2

= -( -1 ) + 2

= 1 + 2

= 3

If x = -1 the value of -x + 2 = 3

Question:3(iii) Find the value of the following expressions, when $x=-1$ :

Answer:

$\\x^2 + 2x + 1 \\= ( -1 )^2 + 2 \times ( -1 ) + 1 \\= 1 - 2 + 2 \\= 0$

If x = -1 the value of x ² + 2x + 1 = 0

Question:3(iv) Find the value of the following expressions, when $x=-1$ :

Answer:

$\\2x^2 - x - 2 \\= 2\times ( -1 )^2 - ( -1 ) - 2 \\ = 2 + 1 - 2 \\= 1$

So the value at x=-1 is 1

Question: 4(i) If $a=2,b=-2,$ find the value of:

Answer:

a ² + b ²

= ( 2 ) ² + ( -2 ) ²

= 4 + 4

= 8

If a = 2 and b = -2 the value of a ² + b ² = 8

Question: 4(ii) If $a=2,b=-2,$ find the value of:

$a^{2}+ab+b^{2}$

Answer:

$\\a^2 + ab + b^2 \\= 2^2 + 2 \times ( -2 ) + ( -2 )^2 \\= 4 - 4 + 4 \\= 4$

If a = 2 and b = -2 the value of a ² + ab + b ² = 4

Question:4(iii) If $a=2,b=-2,$ find the value of

Answer:

a ² - b ²

= 2 ² - ( -2 ) ²

= 4 - 4

= 0

If a = 2 and b = -2 the value of a ² - b ² = 0

Question: 5(i) When $a=0,b=-1,$ find the value of the given expressions:

Answer:

$\\2a + 2b \\= 2 \times 0 + 2 \times ( -1 ) \\= 0 - 2 \\= -2$

When a = 0 and b = -1 the value of the given expression 2a + 2b = -2

Question: 5(ii) When $a=0,b=-1,$ find the value of the given expressions:

$2a^{2}+b^{2}+1$

Answer:

$\\2a^2 + b^2 + 1 \\= 2 \times 0^2 + ( -1 )2 + 1 \\= 0 + 1 + 1 \\= 2$

When a = 0 and b = -1 the value of the given expression 2a ² + b ² + 1 = 2

Question: 5(iii) When $a=0,b=-1$ , find the value of the given expressions:

$2a^{2}b+2ab^{2}+ab$

Answer:

$\\2a^2b + 2ab^2 + ab \\= 2 \times 0^2 \times ( -1 ) + 2 \times 0 \times ( -1 )^2 + 0 \times ( -1 )\\ = 0 + 0 + 0 \\= 0$

When a = 0 and b = -1 the value of the given expression 2a ² b + 2ab ² + ab = 0

Question:5(iv) When $a=0,b=-1,$ find the value of the given expressions:

Answer:

$\\a^2 + ab + 2 \\= 0^2 + 0 \times ( -1 ) + 2 \\= 0 + 0 + 2 \\= 2$

When a = 0 and b = -1 the value of the given expression a ² + ab + 2 = 2

Question: 6(i) Simplify the expressions and find the value if $x$ is equal to $2$

Answer:

$\\x + 7 + 4( x - 5 ) \\= x + 7 + 4x - 20 \\= 5x - 13 \\= 5 \times 2 - 13 \\= 10 - 13 \\= -3$

If x is equal to 2 the value of x + 7 + 4( x - 5 ) = -3

Question: 6(ii) Simplify the expressions and find the value if $x$ is equal to $2$

Answer:

$\\3( x + 2 ) + 5x - 7 \\= 3x + 6 + 5x - 7 \\= 8x - 1 \\= 8 \times (2) - 1 \\= 16 - 1 \\= 15$

If x is equal to 2 the value of 3( x + 2 ) + 5x - 7 = 15

Question: 6(iii) Simplify the expressions and find the value if $x$ is equal to $2$

Answer:

$\\6x + 5( x - 2 ) \\= 6x + 5x - 10 \\= 11x - 10 \\= 11 \times 2 - 10 \\= 22 - 10 \\= 12$

If x is equal to 2 the value of 6x + 5( x - 2 ) = 12

Question: 6(iv) Simplify the expressions and find the value if $x$ is equal to $2$

$4(2x-1)+3x+11$

Answer:

$\\4( 2x - 1 ) + 3x + 11 \\= 8x - 4 + 3x + 11 \\= 11x + 7 \\= 11 \times 2 + 7 \\= 22 + 7 \\= 29$

If x is equal to 2 the value of 4( 2x - 1 ) + 3x + 11 = 29

Question: 7 Simplify these expressions and find their values if

$x=3,a=-1,b=-2.$

(i) $3x-5-x+9$

(ii) $2-8x+4x+4$

(iii) $3a+5-8a+1$

(iv) $10-3b-4-5b$

(v) $2a-2b-4-5+a$

Answer:

The expression is simplified as follows and also obtained their values

(i)

$\\ 3x - 5 - x + 9 \\= 2x + 4 \\= 2 \times 3 + 4 \\= 10$

(ii)

$\\ 2 - 8x + 4x + 4 \\= 6 - 4x \\= 6 - 4 \times 3 \\= -6$

(iii)

$\\3a + 5 - 8a + 1 \\= -5a + 6 \\= -5 \times ( -1 ) + 6 \\= 5 + 6 \\=11$

(iv)

$\\10 - 3b - 4 - 5b \\= 6 - 8b \\= 6 - 8 \times ( -2 ) \\= 6 + 16 \\= 22$

(v)

$\\2a - 2b - 4 - 5 + a \\= 3a - 2b - 9 \\= 3 \times ( -1 ) - 2 \times ( -2 ) - 9 \\= -3 + 4 - 9 \\= -8$

Question: 8 (i) If $z=10,$ find the value of

$z^{3}-3(z-10)$

Answer:

$\\z^3 - 3( z - 10 ) \\= z^3 - 3z + 30 \\= 10^3 - 3 \times 10 + 30 \\= 1000 - 30 + 30 \\= 1000$

If z = 10 the value of z ³ - 3( z - 10 ) = 1000

Question: 8 (ii) If $p=-10,$ find the value of

Answer:

$\\p^2 - 2p - 100 \\= ( -10 )^2 - 2 \times ( -10 ) - 100 \\= 100 + 20 - 100 \\= 20$

If p = -10 the value of p ² - 2p - 100 = 20

Question: 9 What should be the value of a if the value of $2x^{2}+x-a$ equals to $5$ , when

Answer:

$\\2x^2 + x - a = 5 \\2 \times 0^2 + 0 - a = 5 \\-a = 5 \\a = -5$

Therefore for a = -5 when the value of x=0

Question: 10 Simplify the expression and find its value when $a=5$ and

$b=-3\; .2(a^{2}+ab)+3-ab$

Answer:

$\\2( a^2 + ab ) + 3 - ab \\= 2a^2 + 2ab + 3 - ab \\= 2a^2 + ab + 3 \\= 2 \times 5^2 + 5 \times ( -3 ) + 3 \\= 50 - 15 + 3 \\= 38$

When a = 5 and b = -3 the value 2( a ² + ab ) + 3 - ab = 38

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expression Exercise 12.4

Question:1 Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.

1643021315624

1643021328650

1643021389568

Answer:

1643021404783

The number of segments required to form n of each digits shown above are 5n + 1, 3n + 1 and 5n + 2

When n = 5

$\\5n + 1 = 5 \times 5 + 1 = 26 \\3n + 1 = 3 \times 5 + 1 = 16 \\5n + 2 = 5 \times 5 + 2 = 27$

When n = 10

$\\5n + 1 = 5 \times 10 + 1 = 51 \\3n + 1 = 3 \times 10+ 1 = 31 \\5n + 2 = 5 \times 10 + 2 = 52$

When n = 100

$\\5n + 1 = 5 \times 100 + 1 = 501 \\3n + 1 = 3 \times 100+ 1 = 301 \\5n + 2 = 5 \times 100 + 2 = 502$

Question: 2 Use the given algebraic expression to complete the table of number patterns.

1643021436757

Answer: Below you can find the table of number patterns:

1643021453229

Algebraic Expressions Class 7 Chapter 12-Topics

How Are Expressions Formed?
Terms Of An Expression
Like And Unlike Terms
Monomials, Binomials, Trinomials And Polynomials
Addition And Subtraction Of Algebraic Expressions
Finding The Value Of An Expression
Using Algebraic Expressions – Formulas And Rules

NCERT Solutions for Class 7 Maths Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Integers
Chapter 2	Fractions and Decimals
Chapter 3	Data Handling
Chapter 4	Simple Equations
Chapter 5	Lines and Angles
Chapter 6	The Triangle and its Properties
Chapter 7	Congruence of Triangles
Chapter 8	Comparing quantities
Chapter 9	Rational Numbers
Chapter 10	Practical Geometry
Chapter 11	Perimeter and Area
Chapter 12	Algebraic Expressions
Chapter 13	Exponents and Powers
Chapter 14	Symmetry
Chapter 15	Visualising Solid Shapes

NCERT Solutions for Class 7 Subject Wise

NCERT Solutions for Class 7 Maths

NCERT Solutions for Class 7 Science

Benefits of NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions

You will learn to simplify and solve algebraic expressions in this chapter.
You will also learn the addition and subtraction of algebraic expressions which is helpful in making the expression simpler.
It will help you in your homework as all the NCERT questions including practice questions given below every topic are covered in this article.
There are many questions given below every topic to give you conceptual clarity. In NCERT solutions for Class 7 Maths chapter 12 Algebraic Expressions, you will get solutions to these practice questions also.
You should practice all the NCERT questions including examples. If you facing difficulties in doing so, you can take help from these solutions.

Happy learning!!!

Also Check NCERT Books and NCERT Syllabus here:

Also Read

NCERT Solutions for Class 7 Science Chapter 18 Wastewater Story

NCERT Solutions for Class 7 Science Chapter 17 Forests Our Lifeline

NCERT Solutions for Class 7 Science Chapter 16 Water A Precious Resource

NCERT Solutions for Class 7 Science Chapter 14 Electric Current and Its Effects

NCERT Solutions for Class 7 Science Chapter 13 Motion and Time

NCERT Solutions for Class 7 Science Chapter 12 Reproduction in Plants

Articles

DBSE Time Table 2025, Check Delhi Board Exam Schedule for Class 10 & 12

Dec 20, 2024

TNEA Rank Wise Colleges List 2024 - Tamil Nadu Engineering Rank vs College

Dec 20, 2024

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms

News and Notifications

Class 10 student dies by suicide; parents allege harassment from teachers, peers

Winter vacation for Delhi schools from January 1 to 15; DoE issues guidelines for remedial class

Several Delhi schools receive bomb-threat mail, no suspicious items found

CBSE conducts surprise inspections at 29 schools; most violated board’s affiliation by-laws

Schools in Gurugram, Faridabad to hold classes in hybrid mode due to air pollution

CBSE files police complaint against two Delhi schools for submitting fake land certificates

Several Delhi schools receive bomb threat; fifth incident in nine days

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

OR

Explore Top Colleges Accepting Applications

Applications Open