NCERT Solutions for Class 7 Maths Chapter 2 Arithmetic Expressions

NCERT Solutions for Class 7 Maths Chapter 2 Arithmetic Expressions: Download PDF

Careers360 brings you NCERT Solutions for Class 7 Maths Chapter 2 Arithmetic Expressions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.

Download PDF

NCERT Solutions for Class 7 Maths Chapter 2 Arithmetic Expressions: Exercise Questions

Below are the detailed NCERT Class 7 Maths Chapter 2 Arithmetic Expressions question answers provided in the textbook.

Question 1: Fill in the blanks to make the expressions equal on both sides of the = sign:

(a) 13 + 4 = ____ + 6

(b) 22 + ____ = 6 × 5

(c) 8 × ____ = 64 ÷ 2

(d) 34 – ____ = 25

Solution:

1. Left-hand side: 13 + 4 = 17
   Right-hand side: 6
   So, it lacks 17 - 6 = 11
   Hence, the correct answer is 11.
2. Left-hand side: 22
   Right-hand side: 6 × 5 = 30
   So, it lacks 30 - 22 = 8
   Hence, the correct answer is 8.
3. Left-hand side: 8
   Right-hand side: 64 ÷ 2 = 32
   If we multiply 8 by 4, we will get 32.
   Hence, the correct answer is 4.
4. Left-hand side: 34
   Right-hand side: 25
   So, we have to subtract 34 - 25 = 9
   Hence, the correct answer is 9.

Question 2: Arrange the following expressions in ascending (increasing) order of their values.

(a) 67 – 19

(b) 67 – 20

(c) 35 + 25

(d) 5 × 11

(e) 120 ÷ 3

Solution:

(a) 67 – 19 = 48

(b) 67 – 20 = 47

(c) 35 + 25 = 60

(d) 5 × 11 = 55

(e) 120 ÷ 3 = 40

Here, 40 < 47 < 48 < 55 < 60
So, the increasing order of expressions is:
(e) 120 ÷ 3, (b) 67 – 20, (a) 67 – 19, (d) 5 × 11, (c) 35 + 25

Question 1: Find the values of the following expressions by writing the terms in each case.

(a) 28 – 7 + 8

(b) 39 – 2 × 6 + 11

(c) 40 – 10 + 10 + 10

(d) 48 – 10 × 2 + 16 ÷ 2

(e) 6 × 3 – 4 × 8 × 5

Solution:

Question 2: Write a story/situation for each of the following expressions and find their values.

(a) 89 + 21 – 10

(b) 5 × 12 – 6

(c) 4 × 9 + 2 × 6

Solution:

Question 3(a): For each of the following situations, write the expression describing the situation, identify its terms and find the value of the expression.

Queen Alia gave 100 gold coins to Princess Elsa and 100 gold coins to Princess Anna last year. Princess Elsa used the coins to start a business and doubled her coins. Princess Anna bought jewellery and has only half of the coins left. Write an expression describing how many gold coins Princess Elsa and Princess Anna together have.

Solution:

Required Expression:
100 × 2 + 100 ÷ 2

Calculation (Step by step):
100 × 2 + 100 ÷ 2
= 100 × 2 + 50

= 200 + 50

= 250

Question 3 (b): For each of the following situations, write the expression describing the situation, identify its terms and find the value of the expression.

A metro train ticket between two stations is ₹40 for an adult and ₹20 for a child. What is the total cost of tickets: (i) for four adults and three children? (ii) for two groups having three adults each?

Solution:

(i) Required Expression:
40 × 4 + 20 × 3

Calculation (Step by step):

40 × 4 + 20 × 3

= 160 + 60

= 220

(ii) Required Expression:
40 × 3 + 40 × 3

Calculation (Step by step):

40 × 3 + 40 × 3

= 120 + 120

= 240

Question 3 (c): For each of the following situations, write the expression describing the situation, identify its terms and find the value of the expression.

Find the total height of the window by writing an expression describing the relationship among the measurements shown in the picture.

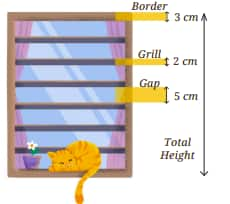
Solution:

There are:
2 Borders, 6 Grills, and 7 Gaps.

Required Expression:
2 × 3 + 2 × 6 + 5 × 7

Calculation (Step by step):
2 × 3 + 2 × 6 + 5 × 7

= 6 + 12 + 35

= 53

Question 1: Fill in the blanks with numbers, and boxes with operation signs such that the expressions on both sides are equal.

(a) 24 + (6 – 4) = 24 + 6 _____

(b) 38 + (_____ _____) = 38 + 9 – 4

(c) 24 – (6 +4) = 24 6 – 4

(d) 24 – 6 – 4 = 24 – 6 _____

(e) 27 – (8 + 3) = 27 8 3

(f) 27– (_____ _____) = 27 – 8 + 3

Solution:

Question 2: Remove the brackets and write the expression having the same value.

(a) 14 + (12 + 10)

(b) 14 – (12 + 10)

(c) 14 + (12 – 10)

(d) 14 – (12 – 10)

(e) –14 + 12 – 10

(f) 14 – (–12 – 10)

Solution:

Question 3: Find the values of the following expressions. For each pair, first try to guess whether they have the same value. When are the two expressions equal?

(a) (6 + 10) – 2 and 6 + (10 – 2)

(b) 16 – (8 – 3) and (16 – 8) – 3

(c) 27 – (18 + 4) and 27 + (–18 – 4)

Solution:

1. 1st value = (6 + 10) – 2 = 16 – 2 = 14
   2nd value = 6 + (10 – 2) = 6 + 8 = 14
   
   Hence, both values are equal.
2. 1st value = 16 – (8 – 3) = 16 – 5 = 11
   2nd value = (16 – 8) – 3 = 8 – 3 = 5
   
   Hence, both values are not equal.
3. 1st value = 27 – (18 + 4) = 27 – 22 = 5
   2nd value = 27 + (–18 – 4) = 27 – 22 = 5
   
   Hence, both values are equal.

Question 4: In each of the sets of expressions below, identify those that have the same value. Do not evaluate them, but rather use your understanding of terms.

(a) 319 + 537, 319 – 537, – 537 + 319, 537 – 319

(b) 87 + 46 – 109, 87 + 46 – 109, 87 + 46 – 109, 87 – 46 + 109, 87 – (46 + 109), (87 – 46) + 109

Solution:

(a)

• $319-537$ and $-537+319$ as this shows the Commutative property of Addition.
• $319+537$ is unique.
• $537-319$ is unique.

(b)

• All 87+46-109 are the same (first three expressions)
• $87-46+109$ and $(87-46)+109$ are the same, as this follows the associative property of addition.
• $87-(46+109)$ is unique.

Question 5: Add brackets at appropriate places in the expressions such that they lead to the values indicated.

(a) 34 – 9 + 12 = 13

(b) 56 – 14 – 8 = 34

(c) –22 – 12 + 10 + 22 = – 22

Solution:

Question 6: Using only the reasoning of how terms change their values, fill the blanks to make the expressions on either side of the equality (=) equal.

(a) 423 + ______= 419 + ______

(b) 207 – 68 = 210 – ______

Solution:

(a)

On the left side, 423 is 4 more than 419 on the right side.
So, we have to add something greater than 4 to add at least 1 on the left side.
Hence, the expression becomes:
423 + 1 = 419 + 5

(b)

210 is 3 more than 207.

To keep equality, the number subtracted must also be 3 more to balance:

Hence, the expression becomes:
207 – 68 = 210 – (68 + 3)
∴ 207 – 68 = 210 – 71

Question 7: Using the numbers 2, 3 and 5, and the operators ‘+’ and ‘–’, and brackets, as necessary, generate expressions to give as many values as possible. For example, 2 – 3 + 5 = 4 and 3 – (5 – 2) = 0.

Solution:

Question 8: Whenever Jasoda has to subtract 9 from a number, she subtracts 10 and adds 1 to it. For example, 36 – 9 = 26 + 1.

(a) Do you think she always gets the correct answer? Why?

(b) Can you think of other similar strategies? Give some examples.

Solution:

(a)
Yes. Jasoda always gets the correct answer.
When she subtracts 10 instead of 9, she subtracts 1 extra. But to balance that, she adds 1.

(b)

Here are some similar strategies.

Question 9: Consider the two expressions:

a) 73 – 14 + 1,

b) 73 – 14 – 1.

For each of these expressions, identify the expressions from the following collection that are equal to it.

(a) 73 – (14 + 1)

(b) 73 – (14 – 1)

(c) 73 + (– 14 + 1)

(d) 73 + (– 14 – 1)

Solution:

a) 73 – 14 + 1 = 60

b) 73 – 14 – 1 = 58
Now,
(a) 73 – (14 + 1) = 58

(b) 73 – (14 – 1) = 60

(c) 73 + (– 14 + 1) = 60

(d) 73 + (– 14 – 1) = 58

So, (b) 73 – (14 – 1) and (c) 73 + (– 14 + 1) are equivalent to 73 – 14 + 1.

Also, (a) 73 – (14 + 1) and (d) 73 + (– 14 – 1) are equivalent to 73 – 14 – 1.

Question 1: Fill in the blanks with numbers and boxes by signs, so that the expressions on both sides are equal.

(a) 3 × (6 + 7) = 3 × 6 + 3 × 7

(b) (8 + 3) × 4 = 8 × 4 + 3 × 4

(c) 3 × (5 + 8) = 3 × 5 ☐ 3 × ____

(d) (9 + 2) × 4 = 9 × 4 ☐ 2 ×____

(e) 3 × (____ + 4) = 3 ____+____

(f) (____+ 6) × 4 = 13 × 4 + ____

(g) 3 × (____+____) = 3 × 5 + 3 × 2

(h) (____+____)×____= 2 × 4 + 3 × 4

(i) 5 × (9 – 2) = 5 × 9 – 5 × ____

(j) (5 – 2) × 7 = 5 × 7 – 2 × ____

(k) 5 × (8 – 3) = 5 × 8 ☐ 5 × ____

(l) (8 – 3) × 7 = 8 × 7 ☐ 3 × 7

(m) 5 × (12 –____) =____ ☐ 5 ×____

(n) (15 –____) × 7 =____ ☐ 6 × 7

(o) 5 × (____–____) = 5 × 9 – 5 × 4

(p) (____–____) × ____= 17 × 7 – 9 × 7

Solution:

Question 2: In the boxes below, fill ‘<’, ‘>’ or ‘=’ after analysing the expressions on the LHS and RHS. Use reasoning and understanding of terms and brackets to figure this out, and not by evaluating the expressions.

(a) (8 – 3) × 29 ☐ (3 – 8) × 29

(b) 15 + 9 × 18 ☐ (15 + 9) × 18

(c) 23 × (17 – 9) ☐ 23 × 17 + 23 × 9

(d) (34 – 28) × 42 ☐ 34 × 42 – 28 × 42

Solution:

Question 3: Here is one way to make 14: 2 × ( 1 + 6 ) = 14. Are there other ways of getting 14? Fill them out below:

(a) _____× (_____+_____) = 14

(b) _____× (_____+_____) = 14

(c) _____× (_____+_____) = 14

(d) _____× (_____+_____) = 14

Solution:
Here are some other ways to make 14.

• (a) 2 × (3 + 4) = 14
• (b) 7 × (1 + 1) = 14
• (c) 1 × (7 + 7) = 14
• (d) 14 × (0 + 1) = 14

Question 4: Find out the sum of the numbers given in each picture below in at least two different ways. Describe how you solved it through expressions.

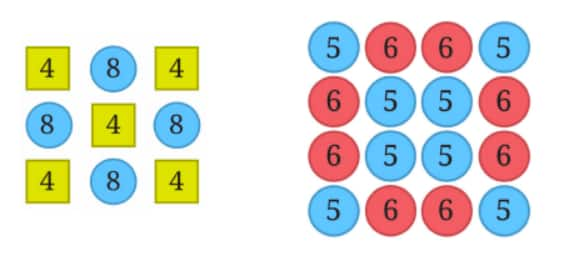
Solution:

1st picture:
4 × 5 + 8 × 4 = 52
Also, we can use the distributive property of multiplication over addition.

4 × (5 + 8) = 52

2nd picture:
5 × 8 + 6 × 8 = 88

Also, we can use the distributive property of multiplication over addition.

8 × (5 + 6) = 88

Question 1 (a): Read the situations given below. Write appropriate expressions for each of them and find their values.
The district market in Begur operates on all seven days of a week. Rahim supplies 9 kg of mangoes each day from his orchard and Shyam supplies 11 kg of mangoes each day from his orchard to this market. Find the amount of mangoes supplied by them in a week to the local district market.

Solution:

Required expression:
9 × 7 + 11 × 7
= 63 + 77
= 140

Hence, the correct answer is 140.

Question 1 (b): Read the situations given below. Write appropriate expressions for each of them and find their values.

Binu earns ₹20,000 per month. She spends ₹5,000 on rent, ₹5,000 on food, and ₹2,000 on other expenses every month. What is the amount Binu will save by the end of a year?

Solution:

Required expression:
12 × {20000 – (5000 + 5000 + 2000)}

= 12 × {20000 – 12000}
= 12 × 8000

= 96000

Hence, the correct answer is 96000.

Question 1 (c): Read the situations given below. Write appropriate expressions for each of them and find their values.

During the daytime a snail climbs 3 cm up a post, and during the night while asleep, accidentally slips down by 2 cm. The post is 10 cm high, and a delicious treat is on its top. In how many days will the snail get the treat?

Solution:

Each day, the snail climbs 3 cm up.
Each night, the snail slips down 2 cm.

So, net climb = 3 – 2 = 1
But, on the last climb of 3 cm, it will reach at the top and in 1 day.
We have to find out how many days the snail to climb the rest of (10 – 3) = 7 cm

Required expression:
(10 – 3) ÷ (3 – 2)
= 7 ÷ 1

= 7
Total days = 7 + 1 = 8 days

Hence, the correct answer is 8.

Question 2: Melvin reads a two-page story every day except on Tuesdays and Saturdays. How many stories would he complete reading in 8 weeks? Which of the expressions below describes this scenario?

(a) 5 × 2 × 8

(b) (7 – 2) × 8

(c) 8 × 7

(d) 7 × 2 × 8

(e) 7 × 5 – 2

(f) (7 + 2) × 8

(g) 7 × 8 – 2 × 8

(h) (7 – 5) × 8

Solution:
Melvin reads a 2-page story each day except Tuesdays and Saturdays.
So, he reads on: 7 – 2 = 5 days per week
Total duration: 8 weeks

The correct expressions are:

• (b) (7 – 2) × 8
• (g) 7 × 8 – 2 × 8

Question 3: Find different ways of evaluating the following expressions:

(a) 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10

(b) 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1

Solution:

Question 4: Compare the following pairs of expressions using ‘<’, ‘>’ or ‘=’ or by reasoning.
(a) 49 – 7 + 8 49 – 7 + 8

(b) 83 × 42 – 18 83 × 40 – 18

(c) 145 – 17 × 8 145 – 17 × 6

(d) 23 × 48 – 35 23 × (48 – 35)

(e) (16 – 11) × 12 –11 × 12 + 16 × 12

(f) (76 – 53) × 88 88 × (53 – 76)

(g) 25 × (42 + 16) 25 × (43 + 15)

(h) 36 × (28 – 16) 35 × (27 – 15)

Solution:

Question 5: Identify which of the following expressions are equal to the given expression without computation. You may rewrite the expressions using terms or removing brackets. There can be more than one expression which is equal to the given expression.

(a) 83 – 37 – 12

(i) 84 – 38 – 12

(ii) 84 – (37 + 12)

(iii) 83 – 38 – 13

(iv) – 37 + 83 –12

(b) 93 + 37 × 44 + 76

(i) 37 + 93 × 44 + 76

(ii) 93 + 37 × 76 + 44

(iii) (93 + 37) × (44 + 76)

(iv) 37 × 44 + 93 + 76

Solution:

(a)
Given expression: 83 – 37 – 12

(b)
Given expression: 93 + 37 × 44 + 76

Question 6: Choose a number and create ten different expressions having that value.

Solution:
Let's choose the number 10.

(1) 5 + 5

(2) 20 – 10

(3) 2 × 5

(4) 50 ÷ 5

(5) (3 × 4) – 2

(6) (12 + 8) ÷ 2

(7) 6 + (8 – 4)

(8) 3 × (6 – 4) + 4

(9) (25 – 5) ÷ 2

(10) (2 + 3) × 2

Arithmetic Expressions Class 7 NCERT Solutions: Topics

Students will explore the following topics in NCERT Class 7 Maths Chapter 2 Arithmetic Expressions:

• Simple Expressions
• Reading and Evaluating Complex Expressions
• Swapping and Grouping
• Swapping the Order of Things in Everyday Life

Class 7 Maths Chapter 2 Arithmetic Expressions Solutions: Extra Question

Question:

Simplify the following expression and find its value when $x=2$:
$4 x+5 x-3+7$

Answer:

$4 x+5 x-3+7$
$=9x+4$
$=9\times(2) + 4$
$=18+4$
$=22$

Hence, the correct answer is 22.

Class 7 Maths NCERT Chapter 2 Arithmetic Expressions: Notes

Careers360 has prepared these Class 7 Arithmetic Expressions Notes to make your revision smoother and faster. Additionally, these notes will help students to understand the Arithmetic Expressions NCERT solutions and solve them on their own from next time.

Arithmetic Expression

An Arithmetic Expression is a mathematical phrase made up of numbers, variables and arithmetic operators, such as addition, subtraction, multiplication, and division.
Every arithmetic expression has a value, which is the number it evaluates to.
Example: 3 + 7 = 9, 12 × 3 = 36

Symbols and their meanings

“=”: This is an “equal to” sign. When the left-hand side is equal to the right-hand side, then an equal sign is used.

“>”: This is a “greater than” sign. We use the greater than sign when one value exceeds the other.

“<”: This is a “less than” sign. We use the less-than sign when one value is lower than another.

Brackets

There are three types of brackets used in Mathematics.

• Parentheses: ( )
• Square Brackets: [ ]
• Curly Brackets: { }

In a mathematical expression, the operations inside the brackets should be performed first. Brackets indicate priority in the order of operations.

When multiple types of brackets are used, the innermost bracket is solved first, followed by the next outer bracket.

Terms without brackets

If there are no brackets in a mathematical expression, then it follows the order below:

Division – Multiplication – Addition – Subtraction

Properties of Mathematical Operations

There is also the distributive property related to multiplication and how it interacts with addition and subtraction. It states that multiplication distributes over addition (and subtraction) in the following way:

Arithmetic Expressions Class 7 NCERT Solutions - Points to Remember

Check the following important points to understand and solve the Class 7 Maths Chapter 2 Arithmetic Expressions question answers effectively.

• The parts of an expression separated by plus (+) or minus (−) signs are called terms.

• A term is a product of its factors, which may be numerical or literal (variables).

• Only like terms can be added or subtracted.

• Perform division and multiplication from left to right.

• Perform addition and subtraction from left to right.

• The BODMAS rule helps to operate in the correct order to simplify an expression to get the value. Using this acronym, we get a clear picture of what operations need to be first, which ones after that, and which are last.
  BODMAS stands for Brackets, Of, Division, Multiplication, Addition, and Subtraction.

• Some important notations:

1. $(+)+(+)=+$

2. $(-)+(-)=-$

3. $(+) \times(+)=+$

4. $(+) \times(-)=-$

5. $(-) \times(-)=+$

NCERT Solutions for Class 7 Maths Chapter Wise

For students' preparation, Careers360 has gathered all Class 7 Maths NCERT solutions here for quick and convenient access.

NCERT Books and NCERT Syllabus

Students can also check the NCERT Books and the NCERT Syllabus here:

• NCERT Syllabus Class 7 Maths
• NCERT Books for Class 7 Maths
• NCERT Books Class 7
• NCERT Syllabus Class 7