NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines
Suppose you are given three intersecting lines that meet at a point; now, imagine the possible scenarios that could arise from this. Also, have you thought about why the angles of certain triangles always seem to be equal? You can find all these answers in Chapter 7, 'A Tale of Three Intersecting Lines' from the NCERT Class 7 Maths textbook, where geometry comes alive. Therefore, it is essential to understand this chapter with a proper understanding and clarity, and this is where the NCERT Solutions for Class 7 Maths come into play.
This Story also Contains
- NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines: Download Free PDF
- NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines (Exercise)
- A Tale of Three Intersecting Lines Class 7 Maths Chapter 7: Topics
- Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines Solutions: Extra Question
- NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines: Notes
- Why are Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines Question Answers Important?
- NCERT Solutions for Class 7 Mathematics Chapter-Wise
- NCERT Books and NCERT Syllabus

These NCERT Solutions provide detailed and step-by-step explanations for the students. With the help of these solutions, they can practice the problems, verify their answer and strengthen their weak areas that need improvement. This will also clear their doubts and provide them with a proper understanding of the chapter's concepts. These NCERT Solutions for Class 7 are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines: Download Free PDF
Careers360 brings you NCERT Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines (Exercise)
Below, you will find the NCERT Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines question answers explained step by step.
|
A Tale of Three Intersecting Lines Class 7 Question answers |
Figure it Out
Question 1: Use the points on the circle and/or the centre to form isosceles triangles.
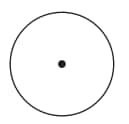
Solution:
Select any two points on the circle and join them to the centre of the circle.
Also, join these points to each other. This will form an isosceles triangle as the two radii are equal in length.
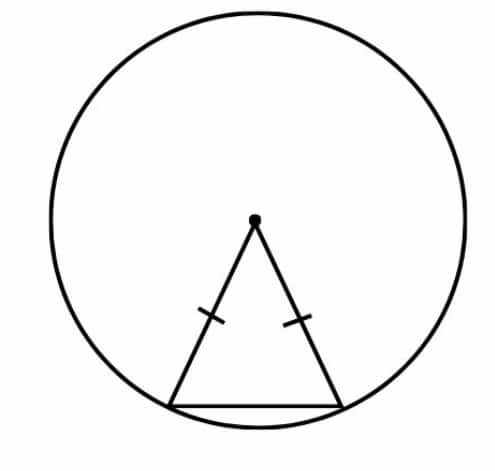
Question 2: Use the points on the circles and/or their centres to form isosceles and equilateral triangles. The circles are of the same size.
Solution:
An isosceles triangle can be formed by connecting the intersecting points of two circles and the centres of either circle.
Here, isosceles triangles are AXY and BXY.
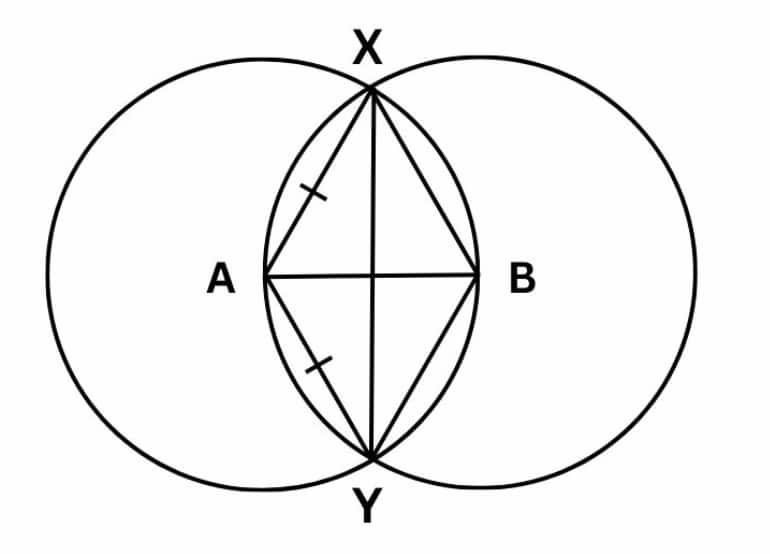
An equilateral triangle can be formed by connecting the centres of the 2 equal circles and one of their intersecting point.
Here, triangle AXB or triangle AYB is an equilateral triangle.
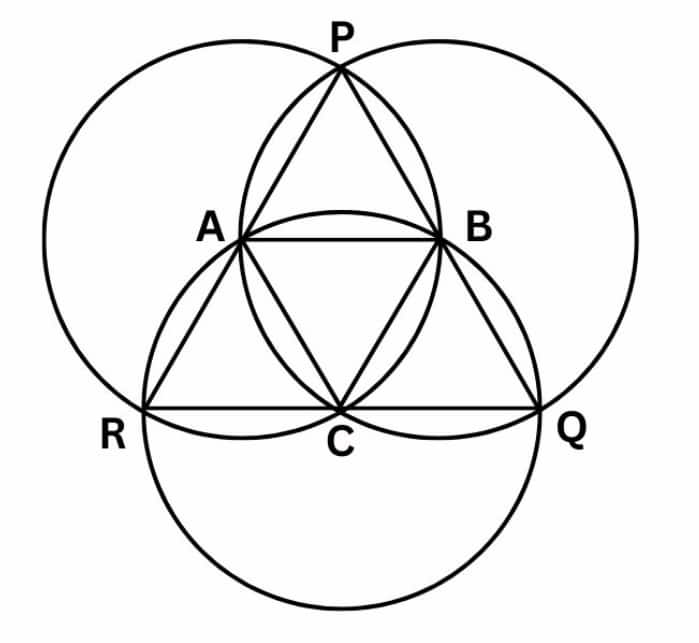
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 154 Number of Questions: 3 |
Question 1: We checked by construction that there are no triangles having sidelengths 3 cm, 4 cm and 8 cm; and 2 cm, 3 cm and 6 cm. Check if you could have found this without trying to construct the triangle.
Solution:
(a) Consider $\mathrm{AB}=4 \mathrm{~cm}, \mathrm{BC}=3 \mathrm{~cm}$ and $\mathrm{AC}=8 \mathrm{~cm}$.
Now, direct path length $=\mathrm{BC}=3 \mathrm{~cm}$
And, roundabout path length $=\mathrm{BA}+\mathrm{AC} =4 \mathrm{~cm}+8 \mathrm{~cm}=12 \mathrm{~cm}$
The direct path length is shorter than the roundabout path length.
Also, direct path length $=A B=4 \mathrm{~cm}$
Roundabout path length $=\mathrm{AC}+\mathrm{BC} =8 \mathrm{~cm}+3 \mathrm{~cm}=11 \mathrm{~cm}$
The direct path length is shorter than the roundabout path length.
Again, direct path length $=A C=8 \mathrm{~cm}$
Then, roundabout path length $=\mathrm{AB}+\mathrm{BC}=4 \mathrm{~cm}+3 \mathrm{~cm} =7 \mathrm{~cm}$
In this case, the direct path is longer than the roundabout path.
So, a triangle cannot exist.
(b) Consider $\mathrm{AB}=3 \mathrm{~cm}, \mathrm{BC}=2 \mathrm{~cm}, \mathrm{AC}=6 \mathrm{~cm}$
If we take the direct path $=A C=6 \mathrm{~cm}$.
And, roundabout path length $=A B+B C =3 \mathrm{~cm}+2 \mathrm{~cm} =5 \mathrm{~cm}$
Since the direct path is longer than the roundabout path.
So, a triangle cannot exist.
Question 2: Can we say anything about the existence of a triangle for each of the following sets of lengths?
(a) 10 km, 10 km and 25 km
(b) 5 mm, 10 mm and 20 mm
(c) 12 cm, 20 cm and 40 cm
You would have realised that using a rough figure and comparing the direct path lengths with their corresponding roundabout path lengths is the same as comparing each length with the sum of the other two lengths. There are three such comparisons to be made.
Solution:
(a) If the direct path is 25 km long, then the roundabout path is $10 \mathrm{~km}+10 \mathrm{~km}=20 \mathrm{~km}$.
Since the direct path cannot be longer than the roundabout path.
Therefore, 10 km, 10 km, and 25 km can't be the side lengths of a triangle.
(b) If the direct path is 20 mm long, then the roundabout path is $5 \mathrm{~mm}+10 \mathrm{~mm}=15 \mathrm{~mm}$.
Since the direct path cannot be longer than the roundabout path.
Therefore, 5 mm, 10 mm, and 20 mm can't be the side lengths of a triangle.
(c) If the direct path is 40 cm long, then the roundabout path is $12 \mathrm{~cm}+20 \mathrm{~cm}=32 \mathrm{~cm}$.
Since the direct path cannot be longer than the roundabout path.
Therefore, 12 cm, 20 cm, and 40 cm can't be the side lengths of a triangle.
Question 3: For each set of lengths seen so far, you might have noticed that in at least two of the comparisons, the direct length was less than the sum of the other two (if not, check again!).
For example, for the set of lengths 10 cm, 15 cm and 30 cm, there are two comparisons where this happens:
10 < 15 + 30
15 < 10 + 30
But this doesn’t happen for the third length: 30 > 10 + 15.
Will this always happen? That is, for any set of lengths, will there be at least two comparisons where the direct length is less than the sum of the other two? Explore different sets of lengths.
Solution:
Yes, for any set of lengths, there will always be at least two comparisons where the direct length is less than the sum of the other two. If two out of three comparisons have a direct length smaller than the sum of the other two, then such a triangle doesn't exist.
However, if all three comparisons have direct length smaller than the sum of the other two, then such a triangle exists.
Let us consider some examples:
(a) 5 cm, 7 cm and 9 cm
$\begin{aligned}
& 5+7>9 \\
& 7+9>5 \\
& 9+5>7
\end{aligned}$
Here, all three comparisons have a direct length smaller than the sum of the other two lengths. Hence, a triangle with the given side lengths exists.
(b) 2 cm, 3 cm and 6 cm
$\begin{aligned}
& 2+3<6 \\
& 3+6>2 \\
& 6+2>3
\end{aligned}$
Here, only two comparisons have a direct length smaller than the sum of the other two lengths. Hence, a triangle with the given side lengths doesn't exist.
(c) 7 cm, 15 cm and 30 cm
$\begin{aligned}
& 7+5<30 \\
& 15+30>7 \\
& 30+7>15
\end{aligned}$
Here, all three comparisons have a direct length smaller than the sum of the other two lengths. Hence, a triangle with the given side lengths doesn't exist.
Question: Further, for a given set of lengths, is it possible to identify which lengths will immediately be less than the sum of the other two, without calculations?
[Hint: Consider the direct lengths in increasing order.]
Solution:
Yes, it is possible to identify which length will be immediately less than the sum of the other two by simply arranging the direct lengths in increasing order.
Question: Given three sidelengths, what do we need to compare to check for the existence of a triangle?
Solution:
Compare each length with the sum of the other two:
$a<b+c$
$b<a+c$
$c<a+b$
If all three conditions are true, a triangle exists. [This is called the triangle inequality]
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 156 Number of Questions: 1 |
Figure it Out
Question 1: Which of the following lengths can be the sidelengths of a triangle? Explain your answers. Note that for each set, the three lengths have the same unit of measure.
(a) 2, 2, 5
(b) 3, 4, 6
(c) 2, 4, 8
(d) 5, 5, 8
(e) 10, 20, 25
(f) 10, 20, 35
(g) 24, 26, 28
Solution:
A set of lengths can be the side lengths of a triangle if each length < the sum of the other two lengths.
(a) $2<5+2$ but $5>2+2$
So, 2, 2, 5 cannot be the side lengths of a triangle.
(b) $3<4+6,4<3+6,6<4+3$
So, 3, 4, and 6 can be the side lengths of a triangle.
(c) $2<4+8,4<2+8$, but $8>4+2$
So, 2, 4, 8 cannot be the side lengths of a triangle.
(d) $5<5+8,8<5+5$
So, 5, 5, 8 can be the side lengths of a triangle.
(e) $10<20+25,20<25+10,25<10+20$
So, 10, 20, and 25 can be the side lengths of a triangle.
(f) $10<20+35,20<10+35$, but $35>10+20$
So, 10, 20, and 35 cannot be the side lengths of a triangle.
(g) $24<26+28,26<24+28,28<24+26$
So, 24, 26, and 28 can be the side lengths of a triangle.
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 159 Number of Questions: 3 |
Figure it Out
Question 1: Check if a triangle exists for each of the following sets of lengths:
(a) 1, 100, 100 (b) 3, 6, 9 (c) 1, 1, 5 (d) 5, 10, 12
Solution:
We know that when each length is smaller than the sum of the other two, we say that the lengths satisfy the triangle inequality, and when a set of lengths satisfies the triangle inequality, then a triangle exists.
(a) Here $1<100+100,100<100+1$
So, for side lengths 1, 100, 100, a triangle exists.
(b) $3<6+9,6<3+9$, but $9=6+3$
So, for side lengths $3,6,9$, a triangle does not exist.
(c) $1<1+5$, but $5>1+1$
So, for side lengths 1, 1, 5, a triangle does not exist.
(d) $5<10+12,10<5+12,12<10+5$
So, for side lengths 5, 10, and 12, a triangle exists.
Question 2: Does there exist an equilateral triangle with sides 50, 50, 50? In general, does there exist an equilateral triangle of any sidelength? Justify your answer.
Solution:
Yes, an equilateral triangle with sides 50, 50, and 50 can exist because each side ( 50 ) is less than the sum of the other two sides (50 + 50 = 100), which satisfies the triangle inequality.
Yes, an equilateral triangle can be constructed of any sidelength, satisfying the triangle inequality.
Question 3: For each of the following, give at least 5 possible values for the third length so there exists a triangle having these as sidelengths (decimal values could also be chosen):
(a) 1, 100 (b) 5, 5 (c) 3, 7
Solution:
(a) 5 possible values for the third length would be 99.5, 99.8, 100, 100.5, 100.9
Since, $100<1+99.5,100<1+99.8,100<1+100,100<1+100.5$, and $100<1+100.9$
(b) 5 possible values for the third length would be 1, 3.5, 5, 7.5, 8.9
Since, $5<1+5,5<5+3.5,5<5+5,5<5+7.5$, and $5<5+8.9$
(c) 5 possible values for the third length would be 4.5, 5, 6.9, 8, 9.8
Since, $7<3+4.5,7<5+3,7<3+6.9,7<3+8,7<3+9.8$
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 161 Number of Questions: 1 |
Figure it Out
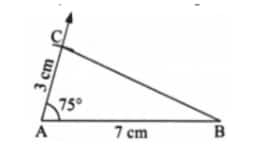
Question 1: Construct triangles for the following measurements, where the angle is included between the sides: (a) 3 cm, 75°, 7 cm; (b) 6 cm, 25°, 3 cm; (c) 3 cm, 120°, 8 cm
Solution:
(a) 3 cm, 75°, 7 cm
Step 1: Construct a side AB of length 7 cm.
Step 2: Construct $\angle\mathrm{A}=75^{\circ}$ by drawing the other arm of the angle.
Step 3: Mark the point $C$ on the other arm such that AC = 3 cm.
Step 4: Join BC to get the required triangle.
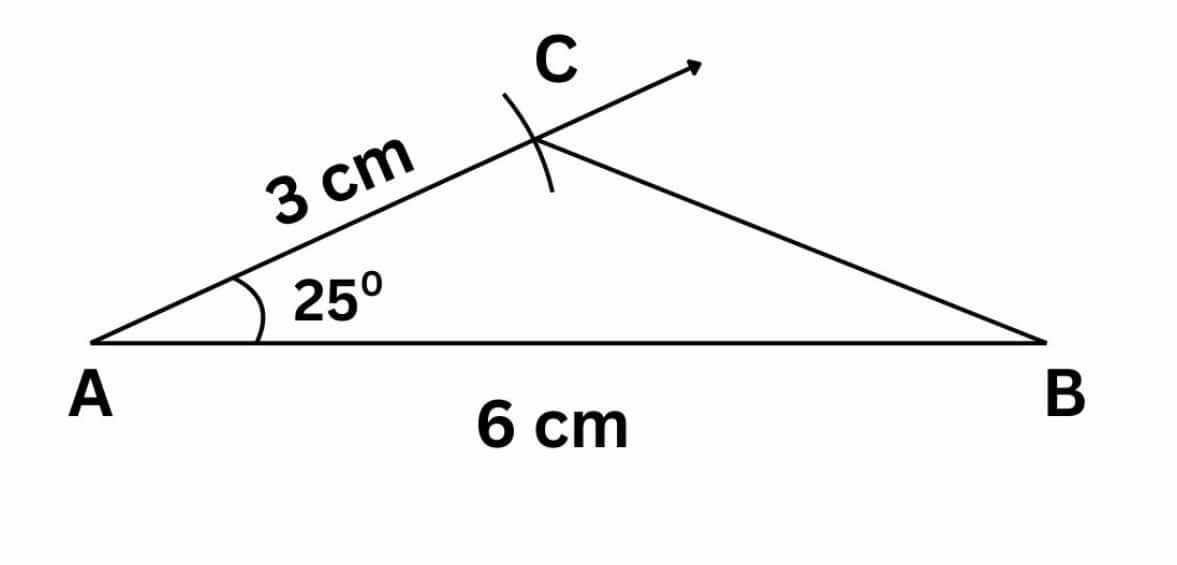
(b) 6 cm, 25°, 3 cm
Step 1: Construct a side AB of length 6 cm.
Step 2: Construct $\angle\mathrm{A}=25^{\circ}$ by drawing the other arm of the angle.
Step 3: Mark the point $C$ on the other arm such that AC = 3 cm.
Step 4: Join BC to get the required triangle.
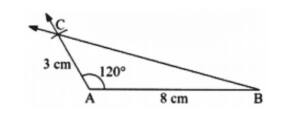
(c) 3 cm, 120°, 8 cm
Step 1: Construct a side AB of length 8 cm.
Step 2: Construct $\angle\mathrm{A}=120^{\circ}$ by drawing the other arm of the angle.
Step 3: Mark the point $C$ on the other arm such that AC = 3 cm.
Step 4: Join BC to get the required triangle.
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 162 Number of Questions: 1 |
Figure it Out
Question 1: Construct triangles for the following measurements:
(a) 75°, 5 cm, 75° (b) 25°, 3 cm, 60° (c) 120°, 6 cm, 30°
Solution:
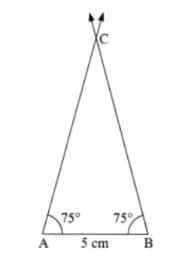
(a) 75°, 5 cm, 75°
(i) Draw the base AB of length 5 cm.
(ii) Draw $\angle \mathrm{A}$ and $\angle \mathrm{B}$ both of measures $45^{\circ}$ each.
(iii) The point of intersection of the two new line segments is the third vertex $C$.
(b) 25°, 3 cm, 60°
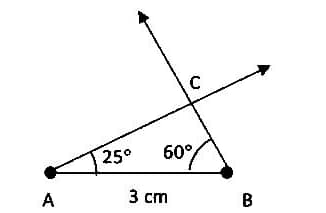
(i) Draw the base AB of length 3 cm.
(ii) Draw $\angle \mathrm{A}$ and $\angle \mathrm{B}$ of measures $25^{\circ}$ and $60^{\circ}$ respectively.
(iii) The point of intersection of the two new line segments is the third vertex C.
(c) 120°, 6 cm, 30°
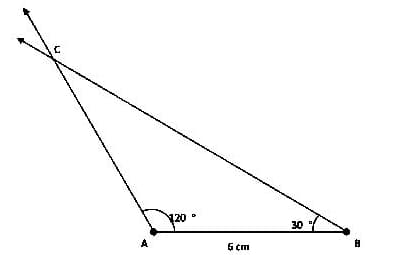
(i) Draw the base AB of length 6 cm.
(ii) Draw $\angle \mathrm{A}$ and $\angle \mathrm{B}$ of measures $120^{\circ}$ and $30^{\circ}$ respectively.
(iii) The point of intersection of the two new line segments is the third vertex C.
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 163 Number of Questions: 2 |
Figure it Out
Question 1: For each of the following angles, find another angle for which a triangle is (a) possible, (b) not possible. Find at least two different angles for each category: (a) 30° (b) 70° (c) 54° (d) 144°
Solution:
(i) $30^{\circ}$
A triangle is possible when another angle is less than $150^{\circ}$. Examples of angles are $120^{\circ}$ and $85^{\circ}$.
A triangle is not possible when another angle is greater than or equal to $150^{\circ}$. Examples of angles are $165^{\circ}$ and $170^{\circ}$.
(ii) $70^{\circ}$
A triangle is possible when another angle is less than $110^{\circ}$. Examples of angles are $100^{\circ}$ and $67^{\circ}$.
A triangle is not possible when another angle is greater than or equal to $110^{\circ}$. Examples of angles are $135^{\circ}$ and $150^{\circ}$.
(iii) $54^{\circ}$
A triangle is possible when another angle is less than $126^{\circ}$. Examples of angles are $105^{\circ}$ and $95^{\circ}$.
A triangle is not possible when another angle is greater than or equal to $126^{\circ}$. Examples of angles are $139^{\circ}$ and $145^{\circ}$.
(iv) $144^{\circ}$
A triangle is possible when another angle is less than $36^{\circ}$. Examples of angles are $20^{\circ}$ and $35^{\circ}$.
A triangle is not possible when another angle is greater than or equal to $36^{\circ}$. Examples of angles are $65^{\circ}$ and $45^{\circ}$.
Question 2: Determine which of the following pairs can be the angles of a triangle and which cannot:
(a) 35°, 150°, (b) 70°, 30°, (c) 90°, 85°, (d) 50°, 150°
Solution:
(a) $35^{\circ}, 150^{\circ}$
$35^{\circ}+150^{\circ}=185^{\circ}>180^{\circ}$. Not possible.
(b) $70^{\circ}, 30^{\circ}$
$70^{\circ}+30^{\circ}=100^{\circ}<180^{\circ}$. Possible.
(c) $90^{\circ}, 85^{\circ}$
$90^{\circ}+85^{\circ}=175^{\circ}<180^{\circ}$. Possible.
(d) $50^{\circ}, 150^{\circ}$
$50^{\circ}+150^{\circ}=200^{\circ}>180^{\circ}$. Not possible.
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 165 Number of Questions: 3 |
Figure it Out
Question 1: Find the third angle of a triangle (using a parallel line) when two of the angles are:
(a) 36°, 72°, (b) 150°, 15°, (c) 90°, 30°, (d) 75°, 45°
Solution:
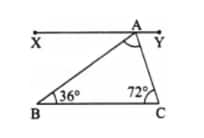
(a) 36°, 72°
Since XY ∥ BC, then:
∠ ABC = ∠XAB = 36° ……. (Alternate interior angles)
∠ BCA = ∠YAC = 72° ……. (Alternate interior angles)
∠XAB + ∠BAC + ∠YAC = 180°……… (Sum of angles on a straight line)
⇒ 36° + ∠BAC + 72° = 180°
⇒ 108° + ∠BAC = 180°
⇒ ∠BAC = 180° – 108°
⇒ ∠BAC = 72°.
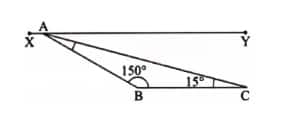
(b) 150°, 15°
Since XY ∥ BC, then:
∠ ABC = ∠XAB = 150° ……. (Alternate interior angles)
∠ BCA = ∠YAC = 15° ……. (Alternate interior angles)
∠XAB + ∠BAC + ∠YAC = 180°……… (Sum of angles on a straight line)
⇒ 150° + ∠BAC + 15° = 180°
⇒ 165° + ∠BAC = 180°
⇒ ∠BAC = 180° – 165°
⇒ ∠BAC = 15°.
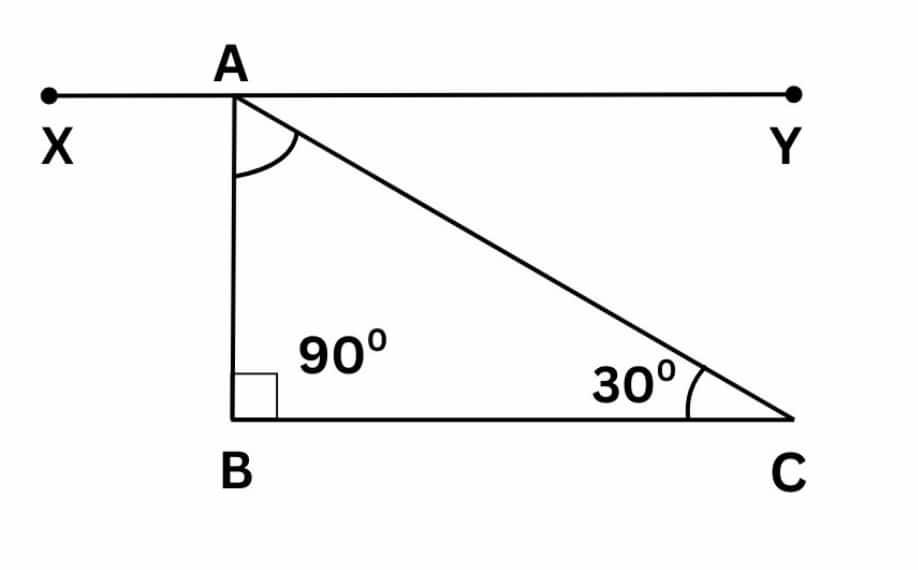
(c) 90°, 30°
Since XY ∥ BC, then:
∠ ABC = ∠XAB = 90° ……. (Alternate interior angles)
∠ BCA = ∠YAC = 30° ……. (Alternate interior angles)
∠XAB + ∠BAC + ∠YAC = 180°……… (Sum of angles on a straight line)
⇒ 90° + ∠BAC + 30° = 180°
⇒ 120° + ∠BAC = 180°
⇒ ∠BAC = 180° – 120°
⇒ ∠BAC = 60°.
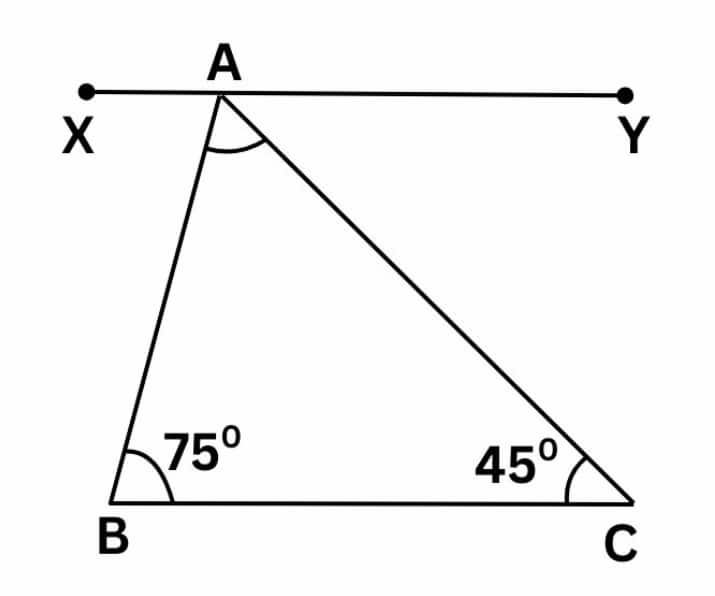
(d) 75°, 45°
Since XY ∥ BC, then:
∠ ABC = ∠XAB = 75° ……. (Alternate interior angles)
∠ BCA = ∠YAC = 45° ……. (Alternate interior angles)
∠XAB + ∠BAC + ∠YAC = 180°……… (Sum of angles on a straight line)
⇒ 75° + ∠BAC + 45° = 180°
⇒ 120° + ∠BAC = 180°
⇒ ∠BAC = 180° – 120°
⇒ ∠BAC = 60°
Question 2: Can you construct a triangle all of whose angles are equal to 70°? If two of the angles are 70°, what would the third angle be? If all the angles in a triangle have to be equal, then what must its measure be? Explore and find out.
Solution:
No, it is not possible to construct a triangle with all angles equal to 70°.
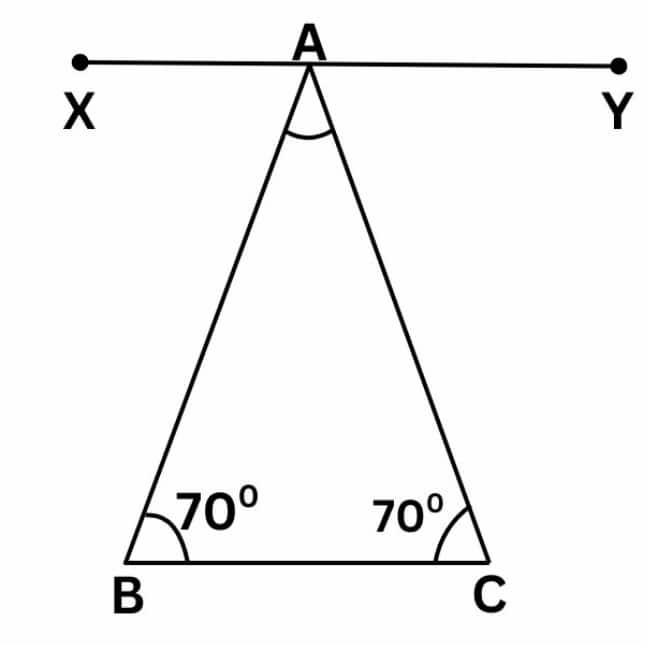
If we take two base angles as $70^{\circ}$ that is, $\angle \mathrm{B}$ and $\angle \mathrm{C}=70^{\circ}$, then we have to find $\angle \mathrm{BAC}$.
Since $X Y$ is parallel to $B C$.
So, $\angle \mathrm{XAB}=\angle \mathrm{B}=70^{\circ}$ $\qquad$
and $\angle \mathrm{YAC}=\angle \mathrm{C}=70^{\circ}$ $\qquad$
Also, $\angle \mathrm{XAB}+\angle \mathrm{BAC}+\angle \mathrm{YAC}=180^{\circ}$
$\Rightarrow 70^{\circ}+\angle \mathrm{BAC}+70^{\circ}=180^{\circ}[$ Using (i) and (ii) $]$
$\Rightarrow \angle B A C=180^{\circ}-140^{\circ}=40^{\circ}$.
So, the third angle would be $40^{\circ}$.
If all the angles in a triangle have to be equal, then each angle must measure $60^{\circ}$.
This type of triangle is called an equilateral triangle.
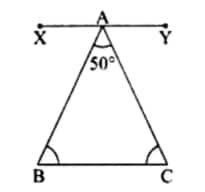
Question 3: Here is a triangle in which we know ∠B = ∠C and ∠A = 50°. Can you find ∠B and ∠C?
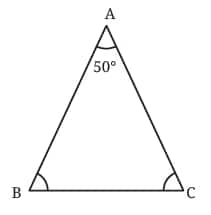
Solution:
Given, ∠B = ∠C and ∠A = 50°
Draw a line XY parallel to BC, then:
∠B = ∠XAB ……. (Alternate interior angles)
∠C = ∠YAC ……. (Alternate interior angles)
∠XAB + ∠A + ∠YAC = 180°……… (Sum of angles on a straight line)
⇒ ∠B + 50° + ∠C = 180°
⇒ ∠C + ∠C = 180° – 50°
⇒ 2∠C = 130°
⇒ ∠C = $\frac{130°}{2}$ = 65°
Therefore, ∠B = ∠C = 65°
| A Tale of Three Intersecting Lines Class 7 Question answers Page number: 170 Number of Questions: 4 |
Figure it Out
Question 1: Construct a triangle ABC with BC = 5 cm, AB = 6 cm, CA = 5 cm. Construct an altitude from A to BC.
Solution:
(i) Draw the base BC = 5 cm.
(ii) From B, draw a long arc of radius 6 cm.
(iii) From C, draw an arc of radius 5 cm intersecting the first arc at point A.
(iv) Point A is the required third vertex. Join AB and AC to get ∆ABC.
(v) Keep the ruler aligned to the base BC. Place the set square on the ruler such that one of the edges of the right angle touches the ruler.
(vi) Slide the set square along the ruler till the vertical edge of the set square touches the vertex A.
(vii) Draw the altitude to BC through A using the vertical edge of the set square.
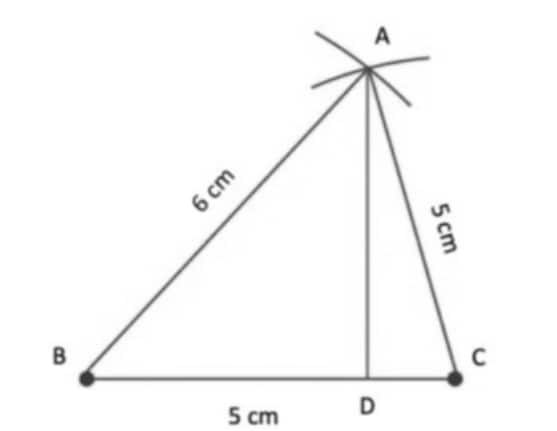
Therefore, in ∆ABC, AC is the required altitude from point A to BC.
Question 2: Construct a triangle TRY with RY = 4 cm, TR = 7 cm, ∠R = 140°. Construct an altitude from T to RY.
Solution:
(i) Construct side TR = 7 cm.
(ii) At point R, draw a ray RA making an angle of 140° with side TR.
(iii) With R as the centre and radius 4 cm, draw an arc intersecting ray RA at point Y.
(iv) Join points T and Y to form triangle ∆TRY.
(v) Keep the ruler aligned to the side RY. Place the set square on the ruler such that one of the edges of the right angle touches the ruler.
(vi) Slide the set square along the ruler till the vertical edge of the set square touches the vertex T.
(vii) Draw the altitude to BC through A using the vertical edge of the set square.
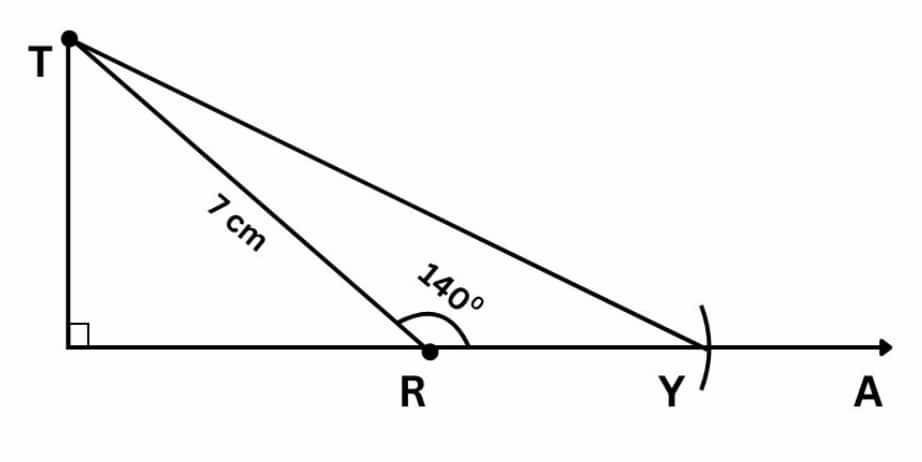
Therefore, in $\triangle$TRY, TB is the required altitude from point T to RY.
Question 3: Construct a right-angled triangle ∆ABC with ∠B = 90°, AC = 5 cm. How many different triangles exist with these measurements?
[Hint: Note that the other measurements can take any values. Take AC as the base. What values can ∠A and ∠C take so that the other angle is 90°?]
Solution:
In a right-angled triangle, if ∠B = 90° and AC = 5 cm, then by the angle sum property of triangles, ∠A + ∠C = 90°.
Since ∠A and ∠C can take various pairs of values that sum to 90°, this results in infinitely many right-angled triangles of different shapes.
For example:
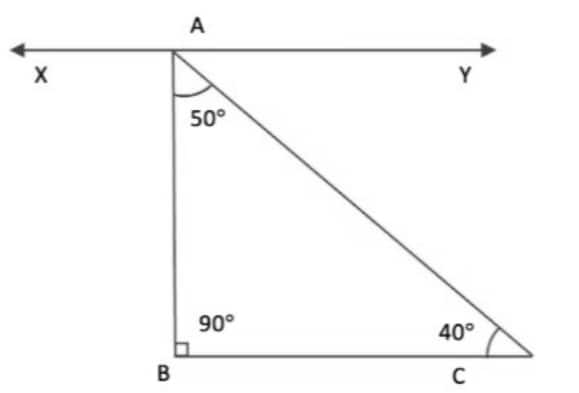
△ABC is a right-angled triangle with ∠B = 90°, AC = 5 cm, ∠A = 50°, and ∠C = 40°, such that
∠A + ∠C = 50° + 40° = 90°.
Question 4: Through construction, explore if it is possible to construct an equilateral triangle that is
(i) right-angled, (ii) obtuse-angled.
Also construct an isosceles triangle that is (i) right-angled, (ii) obtuse-angled.
Solution:
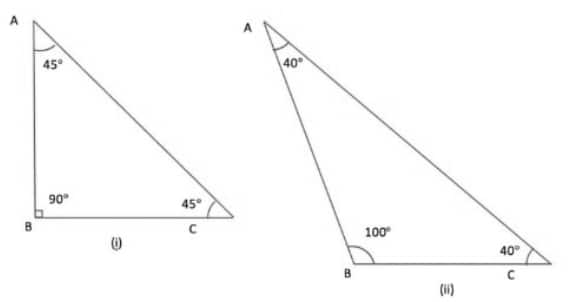
An equilateral triangle has each of its angles equal to 60°, so it is impossible to construct a right-angled or obtuse-angled equilateral triangle.
An isosceles triangle can be right-angled, with one angle of 90° and the other two angles of 45° each.
An isosceles triangle can also be obtuse-angled, with one angle of 100° and the other two angles of 40° each.
A Tale of Three Intersecting Lines Class 7 Maths Chapter 7: Topics
The important topics that are covered in NCERT Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines are:
- Triangles
- Equilateral Triangles
- Constructing a Triangle When its Sides are given
- Triangle Inequality
- Visualising the Construction of Circles
- Construction of Triangles When Some Sides and Angles are Given
- Angle Sum Property
- Exterior Angles Property
- Constructions Related to Altitudes of Triangles
- Types of Triangles
Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines Solutions: Extra Question
Question:
In a triangle, two angles measure $50^{\circ}$ and $60^{\circ}$. Find the measure of the third angle.
Solution:
We know the Angle Sum Property of a Triangle:
The sum of all three angles in a triangle is $= 180^\circ$
Let the third angle be $x$.
$50^{\circ}+60^{\circ}+x=180^{\circ}$
$⇒110^{\circ}+x=180^{\circ}$
$⇒x=180^{\circ}-110^{\circ}$
$\therefore x =70^{\circ}$
Hence, the correct answer is $70^{\circ}$.
NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines: Notes
Careers360 has prepared these Class 7 A Tale of Three Intersecting Lines Notes to make your revision smoother and faster. Additionally, these notes will help students understand the A Tale of Three Intersecting Lines NCERT solutions and solve them independently from next time.
|
Theorem |
Statements |
Related Formula (if any) |
|
Angle Sum Property |
The sum of the interior angles of a triangle is always 180 degrees. |
$\angle{A} + \angle{B} + \angle{C} = 180$ |
|
Triangle inequality theorem |
The sum of the lengths of any two sides of a triangle is greater than the length of the third side. |
$a+b>c,b+c>a,c+a>b$ where a, b, and c are the sides of the triangle. |
|
Pythagoras Theorem |
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. |
$c^2=a^2+b^2$ where c is the longest side of the right-angled triangle and b and a are the other two sides. |
|
Exterior Angle Theorem |
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles. |
$\angle{D} = \angle{A} + \angle{B}$ where D is the exterior angle and B and A are the opposite interior angles. |
Angle Sum Property
The sum of the interior angles of a triangle is always 180 degrees.
Proof:
Let’s draw a line PQ that passes through the vertex A and is parallel to side BC of the triangle ABC. We know that the sum of the angles on a straight line equals 180°.
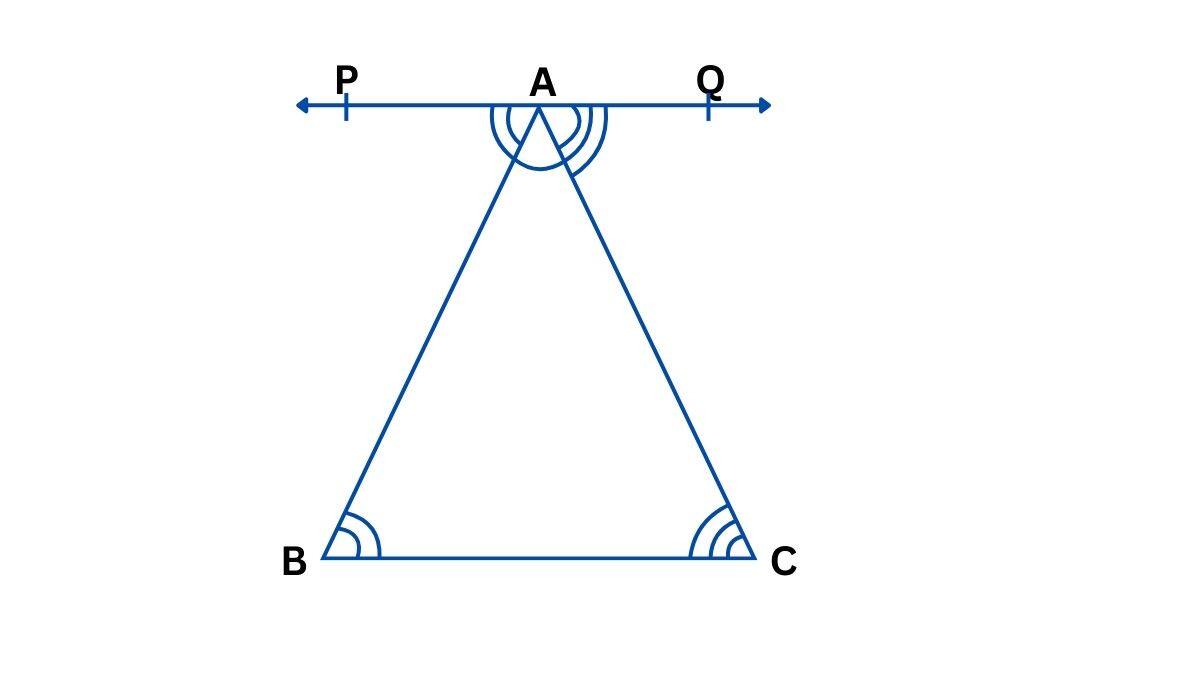
In other words, ∠PAB + ∠BAC + ∠QAC = 180° ………..(1)
Now, since the line PQ is parallel to BC,
∠PAB = ∠ABC and ∠QAC = ∠ACB. (Interior alternate angles)
Substituting these values in equation (1), we get,
∠ABC + ∠BAC + ∠ACB = 180°
Hence, the sum of the angles of a triangle is 180°. (proved)
Triangle inequality theorem
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Proof:
Let ABC be a triangle; we need to prove that AB + AC > BC.
Extend BA to point D such that AD = AC, and join C to D.
We note that ∠ACD = ∠ADC, which means that in triangle BCD, ∠BCD > ∠BDC.
Sides opposite to larger angles are larger, i.e. BD > BC
⇒ AB + AD > BC
⇒ AB + AC > BC (as AD = AC)
Hence, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. (proved)
Types of Triangles
Why are Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines Question Answers Important?
The chapter, A Tale of Three Intersecting Lines, helps us understand how different lines and angles in triangles meet and relate to each other. It also teaches us how to draw and study triangles carefully. These Class 7 Maths chapter 7 A Tale of Three Intersecting Lines question answers make learning these ideas easier through examples and practice questions.
- These solutions help us understand the properties of triangles, such as angles, sides, and types of triangles.
- Students learn how to construct triangles and related figures, which improves their drawing and measurement skills.
- Dealing with Class 7 Maths chapter 7 A Tale of Three Intersecting Lines question answers builds a strong base for higher classes when we study geometry in detail.
NCERT Solutions for Class 7 Mathematics Chapter-Wise
We at Careers360 compiled all the NCERT class 7 Maths solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and NCERT Syllabus
Students can also check the Class 7 NCERT Books and the NCERT Syllabus here:
Frequently Asked Questions (FAQs)
The exterior angle of a triangle is formed when one side is extended outward.
It equals the sum of the two opposite interior angles.
Example: If the opposite interior angles are 40° and 50°, the exterior angle = 90°.
An altitude is a perpendicular drawn from a vertex to the opposite side or its extension. Each triangle has three altitudes, which may intersect inside, on, or outside the triangle depending on its type.
The triangle inequality states that the sum of the lengths of any two sides of a triangle is always greater than the third side.
Mathematically:
a + b > c, b + c > a, and c + a > b
The Angle Sum Property of a Triangle states that:
The sum of the three interior angles of a triangle is always 180°.
The main topics covered in the NCERT Class 7 Maths chapter 7 A tale of Intersecting Lines are:
- Triangles
- Equilateral Triangles
- Triangle Inequality
- Visualising the Construction of Circles
- Angle Sum Property and Exterior Angles Property
- Triangles and their types
Here are some methods you can use to practice Chapter 7 of Class 7 Maths, A Tale of Three Intersecting Lines efficiently.
- Understand all the concepts and formulas related to it.
- Analyse the solved examples and understand the method of solving
- Solve all the exercises in the NCERT textbook on your own at first.
- If you get stuck, get help from the teachers or friends.
- Always draw diagrams to understand the question better and solve it efficiently.
Careers360 experts have prepared all the solutions in a student-friendly manner, and a step-by-step explanation is also given so that students can understand the solutions easily. You can access the links to those solutions from the tail end of this article.
No, if the sum of two sides equals the third side, the triangle becomes a straight line, and it is not a valid triangle.
For example: Three sides, 5 cm, 3 cm, and 8 cm cannot construct a triangle because 5 cm + 3 cm = 8 cm
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
