NCERT Solutions for Class 7 Maths Chapter 13 Visualising Solid Shapes
Have you ever wondered how architects design a building or how engineers create a 3D model of the building even before construction??? The concept of visualizing solid shapes plays a crucial role in these. Visualizing solid shapes is one of the essential skills in our day-to-day life, like arranging a set of items, packing certain items, assembling furniture, and so on. This interesting chapter helps students explore different types of 3D shapes like cubes, cuboids, cylinders, cones, etc. and their properties. It mainly focuses on the representation of these shapes in different views like top view, bottom view and side view. The NCERT Solutions of this chapter provide a clear explanation and step-by-step solutions for all the exercise questions.
This Story also Contains
- NCERT Solutions for Maths Chapter 13 Visualising Solid Shapes Class 7 - Notes
- NCERT Solutions for Maths Chapter 13 Visualising Solid Shapes Class 7
- NCERT Solutions for Class 7 Maths Chapter 13 Exercise
- Visualising Solid Shapes Class 7 Chapter 13-Topics
- NCERT Solutions for Class 7 Maths Chapter 13 Visualizing Solid Shapes - Points to Remember
- NCERT Solutions for Class 7 Maths Chapter Wise
- NCERT Solutions for Class 7 Subject Wise
- NCERT Books and NCERT Syllabus
These solutions will provide you with step-by-step explanations with conceptual clarity. These solutions are completely reliable as it is created by subject matter experts at Careers360. Students can also refer to NCERT Solutions for Class 7 Maths which give the step-by-step solution aligning the latest syllabus to all the chapters of Class 7 Maths.
NCERT Solutions for Maths Chapter 13 Visualising Solid Shapes Class 7 - Notes
Plane figures ⇒ 2D
Solid shapes ⇒ 3D
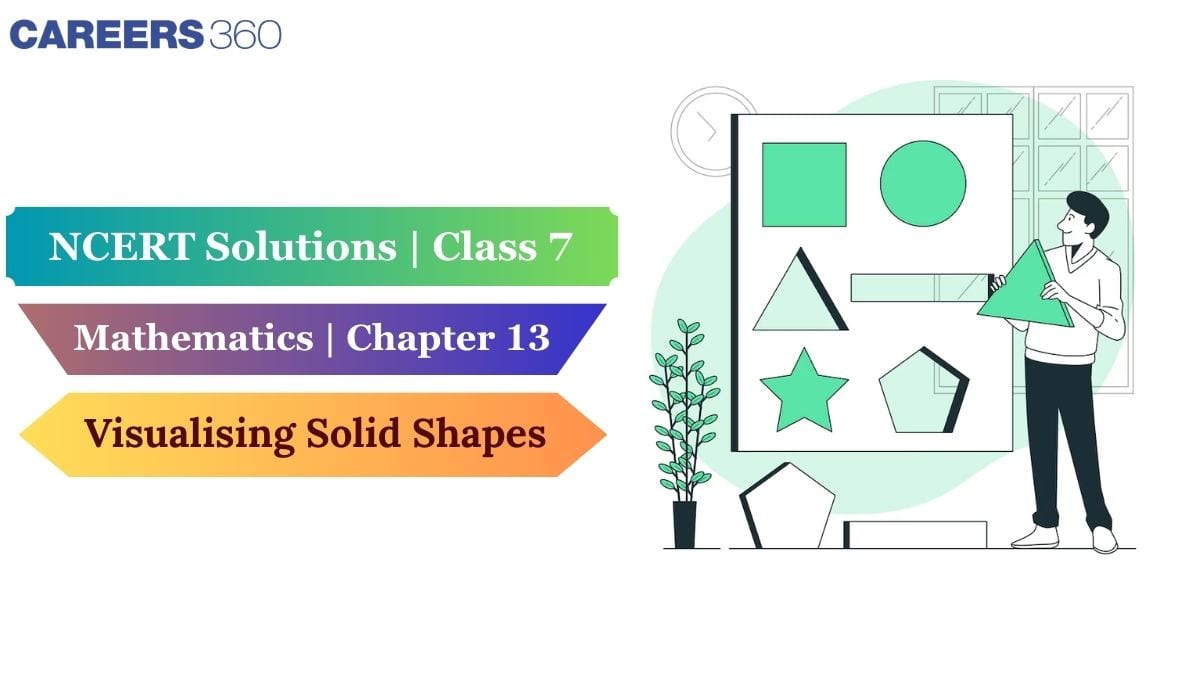
Cube: It is a 3D shape with 6 square faces, 12 edges and 8 vertices. It has equal length, breadth, and height as each face is a square. A dice is an example of a cube.
Cuboid: It is a 3D shape with 6 rectangular faces, 12 edges, and 8 vertices. Its length, breadth, and height are unequal, and opposite faces are equal in area. A matchbox or a book is an example of a cuboid.

Cone: It is a 3D shape with one circular face (base), one curved surface, and one vertex (tip). It tapers smoothly from the base to the vertex. An ice cream cone is an example of a cone.

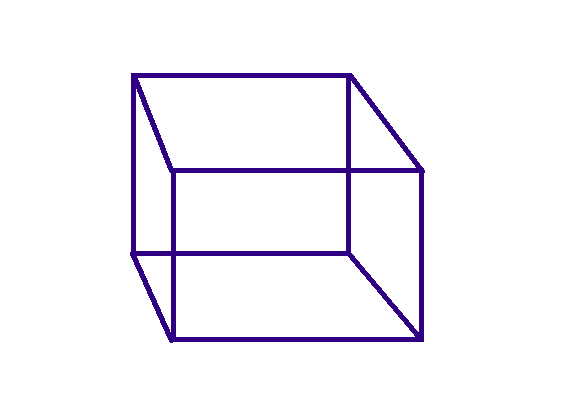
Sphere: It is a perfectly round 3D shape with no edges or vertices and one continuous curved surface. All points on its surface are equidistant from its centre. A ball is an example of a sphere.
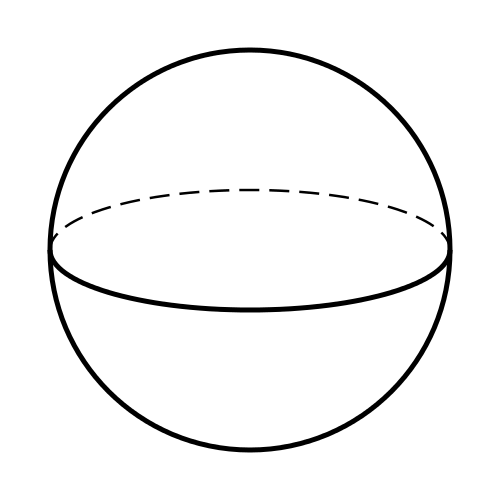
Cylinder: A cylinder is a 3D shape with 2 edges and no vertices. It has 3 faces - two circles and a rectangle wrapped around it. The top view of the cylinder is a circle. The vertical cross-section of the cylinder is rectangular in shape and the horizontal cross-section is circular in shape.
NCERT Solutions for Maths Chapter 13 Visualising Solid Shapes Class 7
NCERT Solutions for Class 7 Maths Chapter 13 Exercise
NCERT Solutions for Class 7 Maths Chapter 13 Visualizing Solid Shapes Exercise 13.1 Page Number: 202-203 Number of Questions: 5 |
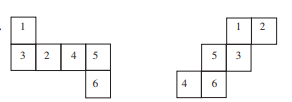
Insert suitable numbers in the blanks, remembering that the numbers on the opposite faces should total 7.
Answer:
The sum of the opposite sides of a dice =7
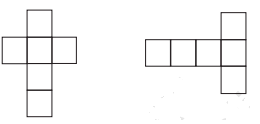
Question: 3 Can this be a net for a die? Explain your answer.
Answer:
NO,
This can not be a net for a die because the opposite faces of a die always have a total sum of 7.
Now, in this case, one pair is 4 opposite to 1
So, their sum is equal to 5 and not equal to 7
Also, the 2nd pair is 6 opposite to 3.
So, their sum is equal to 9 and not equal to 7
Answer:
There are three faces in the given net. The two possibilities of forming nets are
Question: 5 Match the nets with the appropriate solids:

Answer:
These are the correct matches
$(a) \rightarrow (ii)$
$(b) \rightarrow (iii)$
$(c) \rightarrow (iv)$
$(d) \rightarrow (i)$
NCERT Solutions for Class 7 Maths Chapter 13 Visualizing Solid Shapes Exercise 13.2 Page Number: 206-207 Number of Questions: 5 |
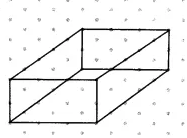
Question: 2 The dimensions of a cuboid are 5 cm, 3 cm and 2 cm. Draw three different isometric sketches of this cuboid.
Answer:
There are a total of 3 isometric sketches of the cuboid that are possible with the given dimensions of a cuboid.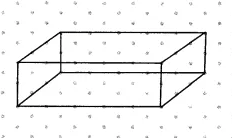
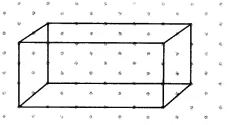
Answer:
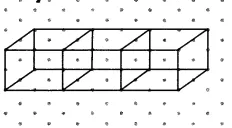
It is given that three cubes, each with a 2 cm edge, are placed side by side to form a cuboid.
So, the oblique sketch of the cuboid is given below.
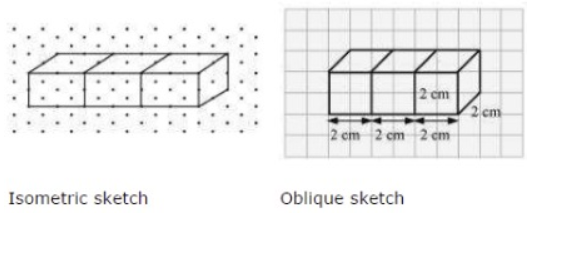
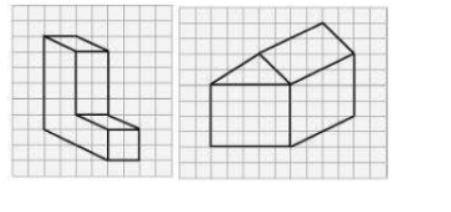
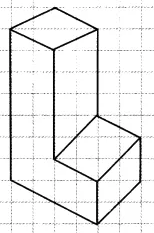
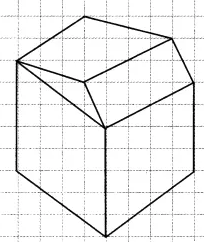
Question: 4 Make an oblique sketch for each one of the given isometric shapes:
Answer:
The oblique sketch for each one of the given isometric shapes is: -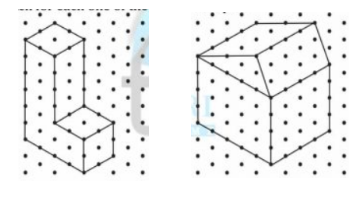
Question: 5 Give (i) an oblique sketch and (ii) an isometric sketch for each of the following:
(a) A cuboid of dimensions 5 cm, 3 cm and 2 cm. (Is your sketch unique?)
(b) A cube with an edge 4 cm long.
An isometric sheet is attached at the end of the book. You could try to make some cubes or cuboids of the dimensions specified by your friend.
Answer:
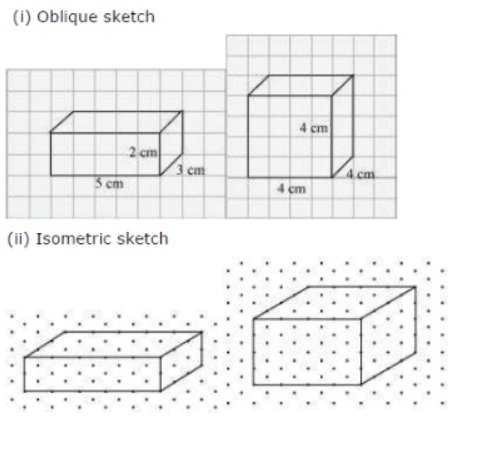
The isometric sketch of s cuboid of dimensions 5 cm, 3 cm and 2 cm. In a similar way, we can draw for the cube also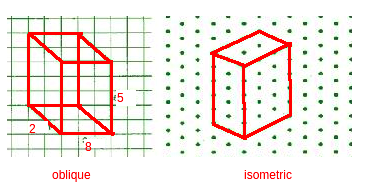
NCERT Solutions for Class 7 Maths Chapter 13 Visualizing Solid Shapes Exercise 13.3 Page Number: 209 Number of Questions: 1 |
Question: 1 What cross-sections do you get when you give a
(i) vertical cut (ii) horizontal cut
to the following solids?
(a) A brick (b) A round apple (c) A die (d) A circular pipe (e) An ice cream cone
Answer:
a) A brick
i) Vertical cut
A vertical cut gives a square or rectangular cross-section
ii) The horizontal cut gives a rectangular cross-section
b) A round apple
In both cases, the cross-section will be circular in shape approximately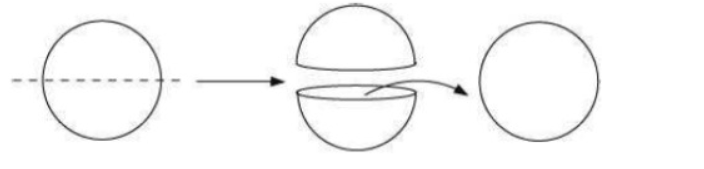
c) A die
Both the cuts will give a square shape.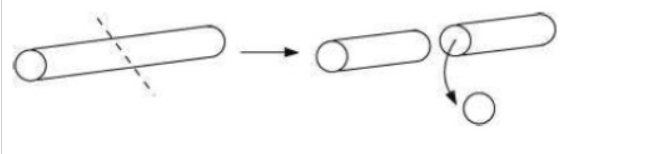
d) A circular pipe
i) A vertical cut will give a circular shape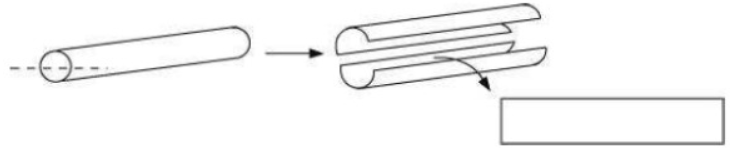
ii) The horizontal cut gives a rectangular shape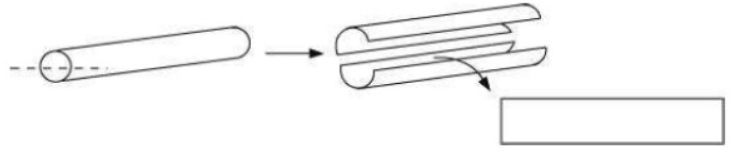
e) An ice cream cone
i) The vertical cut gives a triangular shape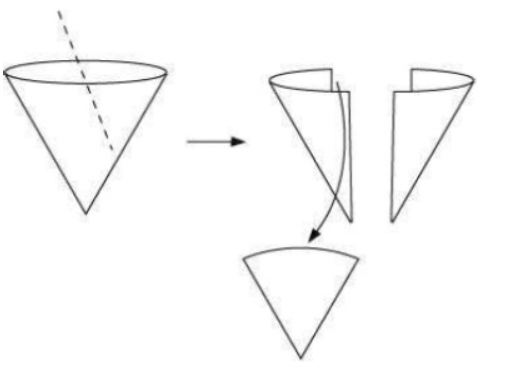
ii) The horizontal cut gives a circular shape
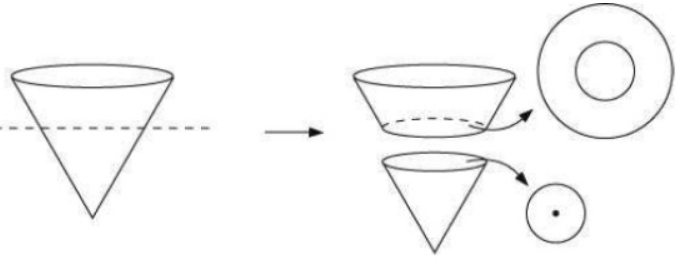
NCERT Solutions for Class 7 Maths Chapter 13 Visualizing Solid Shapes Exercise 13.4 Page Number: 210-211 Number of Questions: 3 |
Question: 3 Examine if the following are true statements:
(i) The cube can cast a shadow in the shape of a rectangle.
(ii) The cube can cast a shadow in the shape of a hexagon.
Answer:
A cube can cast shadows only in the shape of a square.
Therefore, both statements (i) and (ii) are not possible
Visualising Solid Shapes Class 7 Chapter 13-Topics
- Introduction: Plane Figures And Solid Shapes
- Faces, Edges And Vertices
- Nets For Building 3-D Shapes
- Drawing Solids On A Flat Surface
- Oblique Sketches
- Isometric Sketches
- Viewing Different Sections Of A Solid
- One Way To View An Object Is By Cutting Or Slicing
- Another Way Is By Shadow Play
- A Third Way Is By Looking At It From Certain Angles To Get Different Views
NCERT Solutions for Class 7 Maths Chapter 13 Visualizing Solid Shapes - Points to Remember
Vertices: Corner of solid shapes.
Edges: Line segment of solid skeleton.
Faces: Flat surface of a solid.
Oblique Sketch: It does not have proportional lengths of solid.
Isometric Sketch: It has proportional measurements of a solid.
Different Shapes on Shadows: The shadow of a sphere will be circular in shape, the shadow of a cone will be triangular in shape, and the shadow of the cylinder will be rectangular in shape. In simple words, this shadow is known as a plane view of a solid shape.
NCERT Solutions for Class 7 Maths Chapter Wise
NCERT Solutions for Class 7 Subject Wise
Students can access the subject-wise solutions for Class 7 using the links below.
NCERT Books and NCERT Syllabus
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters





