NCERT Solutions for Class 7 Maths Chapter 9 Perimeter and Area

NCERT Solutions for Class 7 Maths Chapter 9 Perimeter and Area - Important Formulae

Perimeter: The total length of the boundary of a two-dimensional shape.

Circumference: The distance around the boundary of a circle.

Area: The measure of the space enclosed by a two-dimensional shape.

Congruent: Two shapes are congruent if they have the same size and shape.

Base: The bottom side of a two-dimensional shape, like a parallelogram or triangle.

Height: The perpendicular distance between the base and the opposite side in a two-dimensional shape.

Diameter: The longest chord (line segment connecting two points on a circle) passing through the centre of a circle.

Radius: The distance from the centre of a circle to any point on its boundary.

Unit Conversions: Converting measurements from one unit to another, based on their relationships.

Unit Conversions:

$\begin{aligned} & 1 \mathrm{~cm}^2=100 \mathrm{~mm}^2 \\ & 1 \mathrm{~m}^2=10000 \mathrm{~cm}^2 \\ & 1 \text { hectare }=10000 \mathrm{~m} ^2\end{aligned}$

Formulas:

Perimeter of a Triangle = Side1 + Side2 + Side3

Perimeter of a Square = 4 × side of the square

Perimeter of a Rectangle = 2 × ( Length + Breadth or Width )

Circumference or Perimeter of a Circle$=\pi d=2 \pi r$ where d = Diameter of circle = 2r, r = Radius of circle

Area of a Square = Side × Side

Area of a rectangle = Length × Breadth

Area of a parallelogram = Base × Height

Area of a Triangle = ($\frac{1}{2}$) × ( Base) × ( Height)

Area of a circle $=\pi r^2$ where, r = Radius of circle

NCERT Solutions for Maths Chapter 9 Perimeter and Area Class 7 - Download PDF

NCERT Solution for Class 7 Maths Chapter 9 (Exercise)

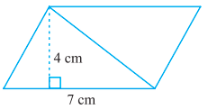
Question: 1(a)Find the area of the following parallelograms:

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 7cm

Height of parallelogram = 4 cm

$\Rightarrow 7 \times 4 = 28 \ cm^2$

Therefore, the area of the parallelogram is $28 \ cm^2$

Question: 1(b) Find the area of the following parallelograms:

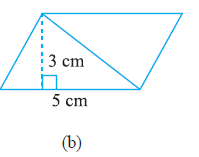
Answer:

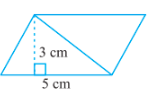
We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 5cm

and

Height of parallelogram = 3 cm

$\Rightarrow 3 \times 5 = 15 \ cm^2$

Therefore, the area of the parallelogram is $15 \ cm^2$

Question: 1(c) Find the area of the following parallelograms:

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 2.5cm

Height of parallelogram = 3.5 cm

$\Rightarrow 3.5 \times 2.5 = 8.75 \ cm^2$

Therefore, the area of the parallelogram is $8.75 \ cm^2$

Question: 1(d) Find the area of the following parallelograms:

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 5cm

Height of parallelogram = 4.8 cm

$\Rightarrow 5 \times 4.8 = 24 \ cm^2$

Therefore, the area of a parallelogram is $24 \ cm^2$

Question: 1(e) Find the area of the following parallelograms:

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 2 cm

Height of parallelogram = 4.4 cm

$\Rightarrow 2 \times 4.4 = 8.8 \ cm^2$

Therefore, the area of a parallelogram is $8.8 \ cm^2$

Question: 2(a) Find the area of each of the following triangles:

Answer: We know that

Area of triangle $=\frac{1}{2}\times base \times height$

Here,

Base of triangle = 4 cm

and

Height of triangle =3 cm

$\Rightarrow \frac{1}{2} \times 4 \times 3 = 6 \ cm^2$

Therefore, the area of the triangle is $6 \ cm^2$

Question: 2(b) Find the area of the following triangles:

Answer: We know that

Area of triangle $=\frac{1}{2}\times base \times height$

Here,

Base of triangle = 5 cm

Height of triangle =3.2 cm

$\Rightarrow \frac{1}{2} \times 5 \times 3.2 = 8 \ cm^2$

Therefore, the area of the triangle is $8 \ cm^2$

Question: 2(c) Find the area of the following triangles:

Answer: We know that

Area of triangle $=\frac{1}{2}\times base \times height$

Here,

Base of triangle = 3 cm

Height of triangle =4 cm

$\Rightarrow \frac{1}{2} \times 3 \times 4 = 6 \ cm^2$

Therefore, the area of the triangle is $6 \ cm^2$

Question: 2(d) Find the area of the following triangles:

Answer: We know that

Area of triangle $=\frac{1}{2}\times base \times height$

Here,

Base of triangle = 3 cm

Height of triangle =2 cm

$\Rightarrow \frac{1}{2} \times 2 \times 3 = 3 \ cm^2$

Therefore, the area of the triangle is $3 \ cm^2$

Question: 3 Find the missing values:

Answer: We know that

Area of parallelogram $= base \times height$

a) Here, the base and area of the parallelogram are given

$\Rightarrow 246= 20 \times height$

$\Rightarrow height = \frac{246}{20}= 12.3 \ cm$

b) Here height and area of the parallelogram are given

$\Rightarrow 154.5= 15 \times base$

$\Rightarrow base = \frac{154.5}{15}=10.3 \ cm$

c) Here height and area of the parallelogram are given

$\Rightarrow 48.72= 8.4 \times base$

$\Rightarrow base = \frac{48.72}{8.4}=5.8 \ cm$

d) Here base and area of the parallelogram are given

$\Rightarrow 16.38= 15.6 \times height$

$\Rightarrow height = \frac{16.38}{15.6}=1.05 \ cm$

Question: 4 Find the missing values:

Answer: We know that

Area of triangle $= \frac{1}{2}\times base \times height$

a) Here, the base and area of the triangle is given

$\Rightarrow 87= \frac{1}{2} \times 15 \times height$

$\Rightarrow height = \frac{87}{7.5}= 11.6 \ cm$

b) Here height and area of the triangle are given

$\Rightarrow 1256= \frac{1}{2}\times 31.4 \times base$

$\Rightarrow base = \frac{1256}{15.7}=80 \ mm$

c) Here base and area of the triangle is given

$\Rightarrow 170.5= \frac{1}{2} \times 22 \times height$

$\Rightarrow height = \frac{170.5}{11}=15.5 \ cm$

Question: 5(a) $PQRS$ is a parallelogram (Fig 11.23). $QM$ is the height from $Q$ to $SR$ and $QN$ is the height from $Q$ to $PS$ . If $SR=12 \; cm$ and

$QM=7.6 \; cm.$ Find: the area of the parallelogram $PQRS$

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 12 cm

Height of parallelogram = 7.6 cm

$\Rightarrow 12 \times 7.6 = 91.2 \ cm^2$

Therefore, the area of the parallelogram is $91.2 \ cm^2$

Question: 5(b) $PQRS$ is a parallelogram (Fig 11.23). $QM$ is the height from $Q$ to $SR$ and $QN$ is the height from $Q$ to $PS$ . If $SR=12 \; cm$ and $QM=7.6 \; cm.$ Find: $QN$ , if $PS=8\; cm$.

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram = 12 cm

Height of parallelogram = 7.6 cm

$\Rightarrow 12 \times 7.6 = 91.2 \ cm^2$

Now,

The area is also given by $QN \times PS$

$\Rightarrow 91.2 = QN \times 8$

$\Rightarrow QN = \frac{91.2}{8} = 11.4 \ cm$

Therefore, the value of QN is $11.4 \ cm$

Question: 6 $DL$ and $BM$ are the heights on sides $AB$ and $AD$ respectively, of parallelogram $ABCD$ (Fig 11.24). If the area of the parallelogram is $1470\; cm^{2}.$ $AB=35\; cm$ and $AD=49\; cm,$ find the length of $BM$ and $DL.$

Answer: We know that

Area of parallelogram $= base \times height$

Here,

Base of parallelogram(AB) = 35 cm

Height of parallelogram(DL) = h cm

$\Rightarrow 1470 = 35 \times h$

$\Rightarrow h = \frac{1470}{35} = 42 \ cm$

Similarly,

The area is also given by $AD \times BM$

$\Rightarrow 1470 = 49 \times BM$

$\Rightarrow BM = \frac{1470}{49} = 30 \ cm$

Therefore, the values of BM and DL are 30cm and 42cm, respectively

Question: 7 $\Delta ABC$ is right-angled at $A$ (Fig 11.25). $AD$ is perpendicular to $BC$ . If $AB=5\; cm,$ $BC=13\; cm$ and $AC=12\; cm,$ Find the area of $\Delta ABC$ . Also, find the length of $AD$.

Answer: We know that

Area of triangle $= \frac{1}{2} \times base \times height$

Now,

When base = 5 cm and height = 12 cm

Then, the area is equal to

$\Rightarrow \frac{1}{2} \times 5 \times 12 = 30 \ cm^2$

Now,

When base = 13 cm and height = AD area remains the same

Therefore,

$\Rightarrow 30= \frac{1}{2} \times 13 \times AD$

$\Rightarrow AD = \frac{60}{13} \ cm$

Therefore, the value of AD is $\frac{60}{3} \ cm$ and the area is equal to $30 \ cm^2$

Question: 8 $\Delta ABC$ is isosceles with $AB=AC=7.5\; cm$ and $BC=9\; cm$ (Fig 11.26). The height $AD$ from $A$ to $BC,$ is $6\; cm,$ Find the area of $\Delta ABC.$ What will be the height from $C$ to $AB$ i.e., $CE$ ?

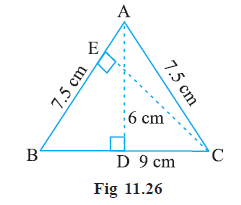
Answer: We know that

Area of triangle $= \frac{1}{2} \times base \times height$

Now,

When base(BC) = 9 cm and height(AD) = 6 cm

Then, the area is equal to

$\Rightarrow \frac{1}{2} \times 9 \times 6 = 27 \ cm^2$

Now,

When base(AB) = 7.5 cm and height(CE) = h , area remain same

Therefore,

$\Rightarrow 27= \frac{1}{2} \times 7.5 \times CE$

$\Rightarrow CE = \frac{54}{7.5}= 7.2 \ cm$

Therefore, the value of CE is 7.2cm and the area is equal to $27 \ cm^2$

Question: 1(a) Find the circumference of the circles with the following radius: (Take $\pi =\frac{22}{7}$ )

$14 \; cm$

Answer: We know that

Circumference of a circle is $= 2\pi r$

$\Rightarrow 2\pi r = 2 \times \frac{22}{7} \times 14 = 88 \ cm$

Therefore, the circumference of the circle is 88 cm

Question: 1(b) Find the circumference of the circles with the following radius: (Take $\pi =\frac{22}{7}$ )

$28\; mm$

Answer: We know that

Circumference of circle is $= 2\pi r$

$\Rightarrow 2\pi r = 2 \times \frac{22}{7} \times 28 = 176 \ mm$

Therefore, the circumference of the circle is 176 mm

Question: 1(c) Find the circumference of the circles with the following radius: (Take $\pi =\frac{22}{7}$ )

$21\; cm$

Answer: We know that

Circumference of circle is $= 2\pi r$

$\Rightarrow 2\pi r = 2 \times \frac{22}{7} \times 21 = 132 \ cm$

Therefore, the circumference of the circle is 132 cm

Question: 2(a) Find the area of the following circles, given that:

$radius=14\; mm$ (Take $\pi =\frac{22}{7}$ )

Answer: We know that

Area of circle is $= \pi r^2$

$\Rightarrow \pi r^2 = \frac{22}{7}\times (14)^2 = 616 \ mm^2$

Therefore, the area of the circle is $616 \ mm^2$

Question: 2(b) Find the area of the following circles, given that:

$diameter=49\; m$

Answer: We know that

Area of circle is $= \pi r^2$

$\Rightarrow \pi r^2 = \frac{22}{7}\times \left ( \frac{49}{2} \right )^2 =1886.5 \ m^2$

Therefore, the area of the circle is $1886.5 \ m^2$

Question: 2(c) Find the area of the following circles, given that:

$radius=5\; cm$

Answer: We know that

Area of circle is $= \pi r^2$

$\Rightarrow \pi r^2 = \frac{22}{7}\times \left (5 \right )^2 =\frac{550}{7} \ cm^2$

Therefore, the area of the circle is $\frac{550}{7} \ cm^2$

Question: 3 If the circumference of a circular sheet is $154\; m,$ find its radius. Also, find the area of the sheet. (Take $\pi =\frac{22}{7}$ )

Answer: It is given that the circumference of a circular sheet is 154 m

We know that

Circumference of circle is $= 2\pi r$

$\Rightarrow 154 = 2\pi r$

$\Rightarrow 154 = 2 \times \frac{22}{7} \times r$

$\Rightarrow r= \frac{49}{2}= 24.5 \ m$

Now,

Area of circle $= \pi r^2$

$\Rightarrow \frac{22}{7}\times \left ( 24.5 \right )^2 = 1886.5 \ m^2$

Therefore, the radius and area of the circle are 24.5 m and $1886.5 \ m^2$ respectively

Question: 4 A gardener wants to fence a circular garden of diameter $21 \; m$. Find the length of the rope he needs to purchase if he makes $2$ rounds of the fence. Also find the cost of the rope, if it costs $Rs.4 \; per \; meter.$ (Take $\pi =\frac{22}{7}$ ).

Answer: It is given that the diameter of a circular garden is $21 \; m$.

We know that

Circumference of circle is $= 2\pi r$

$\Rightarrow 2 \times \frac{22}{7}\times \frac{21}{2} = 66 \ m$

Now, the length of the rope required to make $2$ rounds of fence is

$\Rightarrow 2 \times$ circumference of circle

$\Rightarrow 2 \times 66 = 132 \ m$

Now, cost of rope at $Rs.4 \; per \; meter$ is

$\Rightarrow 132 \times 4 = 528 \ Rs$

Therefore, the length of the rope required to make $2$ rounds of fence is 132 m and the cost of rope at $Rs.4 \; per \; meter$ is Rs 528

Question: 5 From a circular sheet of radius $4\; cm$, a circle of radius $3\; cm$ is removed. Find the area of the remaining sheet.(Take $\pi =3.14$ )

Answer: We know that

Area of circle $= \pi r^2$

Area of circular sheet with radius 4 cm $= 3.14 \times (4)^2 = 50.24 \ cm^2$

Area of the circular sheet with radius 3 cm $= 3.14 \times (3)^2 = 28.26 \ cm^2$

Now,

Area of remaining sheet = Area of the circle with radius 4 cm - Area of the circle with radius 3 cm

$= 50.24 - 28.26 = 21.98\ cm^2$

Therefore, the Area of the remaining sheet is $21.98\ cm^2$

Question: 6 Saima wants to put lace on the edge of a circular table cover of diameter $1.5 \; m$. Find the length of the lace required and also find its cost if one meter of the lace costs $Rs.15.$ (Take $\pi =3.14$ )

Answer: It is given that the diameter of a circular table is 1.5m.

We know that

Circumference of circle is $= 2\pi r$

$\Rightarrow 2 \times \frac{22}{7}\times \frac{1.5}{2} = 4.71 \ m$

Now, the length of the lace required is

$\Rightarrow$ circumference of circle $= 4.71 \ m$

Now, cost of lace at $Rs.15 \; per \; meter$ is

$\Rightarrow 4.71 \times 15 = 70.65 \ Rs$

Therefore, the length of the lace required is 4.71 m and the cost of lace at $Rs.15 \; per \; meter$ is Rs 70.65

Question: 7 Find the perimeter of the adjoining figure, which is a semicircle including its diameter.

Answer: It is given that the diameter of a semicircle is 10 cm.

We know that

Circumference of semi-circle is $= \pi r$

Circumference of a semi-circle with a diameter of 10 cm including diameter is

$\Rightarrow \left ( \frac{22}{7}\times \frac{10}{2} \right )+10 = 15.7+10=25.7 \ cm$

Therefore, the Circumference of a semi-circle with a diameter of 10 cm including a diameter is 25.7 cm

Question: 8 Find the cost of polishing a circular table-top of diameter $1.6\; m$, if the rate of polishing is $Rs.\; 15/m^{2}$. (Take $\pi =3.14$ )

Answer: It is given that the diameter of a circular table is 1.6m.

We know that

Area of circle is $= \pi r^2$

$\Rightarrow 3.14 \times \left ( \frac{1.6}{2} \right )^2 = 2.0096 \ m^2$

Now, the cost of polishing at $Rs.15 \; per \; m^2$ is

$\Rightarrow 2.0096 \times 15 = 30.144 \ Rs$

Therefore, the cost of polishing at $Rs.15 \; per \; m^2$ is Rs 30.144

Question: 9 Shazli took a wire of length $44\; cm$ and bent it into the shape of a circle. Find the radius of that circle. Also, find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take $\pi =\frac{22}{7}$ )

Answer: It is given that the length of the wire is 44 cm

Now, we know that

Circumference of the circle (C) = $2 \pi r$

$\Rightarrow 44 = 2 \pi r$

$\Rightarrow r = \frac{44\times 7}{2 \times 22} = 7 \ cm$

Now,

Area of circle (A) = $\pi r^2$

$\Rightarrow \pi r^2= \frac{22}{7}\times (7)^2= 154 \ cm^2$ - (i)

Now,

Perimeter of square(P) = $4a$

$\Rightarrow 44=4a$

$\Rightarrow a = \frac{44}{4} = 11 \ cm$

Area of sqaure = $a^2$

$\Rightarrow a^2 = (11)^2= 121 \ cm^2$ -(ii)

From equations (i) and (ii) we can clearly see that the area of the circular-shaped wire is more than the square-shaped wire

Question: 10 From a circular card sheet of radius $14\; cm$, two circles of radius $3.5\; cm$ and a rectangle of length $3\; cm$ and breadth $1\; cm$ are removed.(as shown in the adjoining figure). Find the area of the remaining sheet. (Take $\pi =\frac{22}{7}$ )

Answer: It is given that the radius of the circular card sheet is $14\; cm$

Now, we know that

Area of circle (A) = $\pi r^2$

$\Rightarrow \pi r^2= \frac{22}{7}\times (14)^2= 616 \ cm^2$ - (i)

Now,

The area of the circle with a radius of 3.5 cm is

$\Rightarrow \pi r^2= \frac{22}{7}\times (3.5)^2= 38.5 \ cm^2$

Area of two such circle is = $38.5 \times 2 = 77 \ cm^2$ -(ii)

Now, Area of rectangle = $l \times b$

$\Rightarrow l \times b = 3 \times 1 = 3\ cm^2$ -(iii)

Now, the remaining area is (i) - [(ii) + (iii)]

$\Rightarrow 616- [77+3]\Rightarrow 616-80 = 536 \ cm^2$

Therefore, the area of the remaining sheet is $536 \ cm^2$

Question: 11 A circle of radius $2\; cm$ is cut out from a square piece of an aluminium sheet of side $6\; cm$. What is the area of the leftover aluminium sheet?

(Take $\pi =3.14$ )

Answer: It is given that the radius of the circle is $2 \ cm$

Now, we know that

Area of the circle (A) = $\pi r^2$

$\Rightarrow \pi r^2= 3.14 \times(2)^2= 12.56 \ cm^2$ - (i)

Now,

Now, the Area of square = $a^2$

$\Rightarrow a^2 = (6)^2 = 36 \ cm^2$ -(ii)

Now, the remaining area is (ii) - (i)

$\Rightarrow 36 - 12.56 = 23.44 \ cm^2$

Therefore, the area of the remaining aluminium sheet is $23.44 \ cm^2$

Question: 12 The circumference of a circle is $31.4\; cm$. Find the radius and the area of the circle. (Take $\pi =3.14$ )

Answer: It is given that the circumference of the circle is $31.4 \ cm$

Now, we know that

Circumference of circle is = $2 \pi r$

$\Rightarrow 31.4 = 2 \pi r$

$\Rightarrow 31.4 = 2 \times 3.14 \times r$

$\Rightarrow r = 5 \ cm$

Now, the Area of the circle (A) = $\pi r^2$

$\Rightarrow \pi r^2= 3.14 \times(5)^2= 78.5 \ cm^2$

Therefore, the radius and area of the circle are $5 \ cm \ and \ 78.5 \ cm^2$ respectively

Question: 13 A circular flower bed is surrounded by a path $4\; m$ wide. The diameter of the flower bed is $66\; m$. What is the area of this path? $(\pi =3.14)$

Answer: It is given that the diameter of the flower bed is $66\; m$

Therefore, $r = \frac{66}{2} = 33 \ m$

Now, we know that

Area of the circle (A) = $\pi r^2$

$\Rightarrow \pi r^2= 3.14 \times(33)^2= 3419.46\ m^2$ -(i)

Now, Area of outer circle with radius(r ') = 33 + 4 = 37 cm is

$\Rightarrow \pi r'^2= 3.14 \times(37)^2= 4298.66 \ m^2$ -(ii)

The area of the path is equation (ii) - (i)

$\Rightarrow 4298.66-3419.46 = 879.2 \ m^2$

Therefore, the area of the path is $879.2 \ m^2$

Question: 14 A circular flower garden has an area of $314\; m^{2}$. A sprinkler at the centre of the garden can cover an area that has a radius of $12 m$. Will the sprinkler water the entire garden? (Take $\pi =3.14$ )

Answer: It is given that the radius of the sprinkler is $12 m$

Now, we know that

Area of the circle (A) = $\pi r^2$

The area covered by sprinkles is

$\Rightarrow \pi r^2= 3.14 \times(12)^2= 452.16 \ m^2$

And the area of the flower garden is $314\; m^{2}$

Therefore, the sprinkler waters the entire garden

Question: 15 Find the circumference of the inner and the outer circles, shown in the adjoining figure. (Take $\pi =3.14$ )

Answer: We know that

Circumference of circle = $2 \pi r$

Now, the circumference of the inner circle with radius (r) = $19-10=9 \ m$ is

$\Rightarrow 2 \pi r = 2 \times 3.14 \times 9 = 56.52 \ m$

And the circumference of the outer circle with radius (r ') = 19 m is

$\Rightarrow 2 \pi r = 2 \times 3.14 \times 19 = 119.32 \ m$

Therefore, the circumference of the inner and outer circles are $56.52 \ m \ and \ 119.32 \ m$ respectively

Question: 16 How many times a wheel of radius $28\; cm$ must rotate to go $352\; m$? (Take $\pi =\frac{22}{7}$ )

Answer: It is given that the radius of the wheel is $28\; cm$

Now, we know that

Circumference of circle = $2 \pi r$

$\Rightarrow 2 \pi r = 2 \times 3.14 \times 28 = 175.84 \ cm$

Now, the number of rotations done by the wheel to go 352 m is

$\Rightarrow \frac{352 \ m}{175.84 \ cm} = \frac{35200}{175.84}\cong 200$

Therefore, the number of rotations done by the wheel to go 352 m is 200

Question: 17 The minute hand of a circular clock is $15\; cm$ long. How far does the tip of the minute hand move in $1$ hour? (Take $\pi =3.14$ )

Answer: It is given that the minute hand of a circular clock is $15\; cm$ long i.e. ( r = 15 cm)

Now, we know that one hour means a complete circle of minute hand

Now,

Circumference of circle = $2 \pi r$

$\Rightarrow 2 \pi r = 2 \times 3.14 \times 15 = 94.2 \ cm$

Therefore, the distance covered by a minute hand in one hour is 94.2 cm

Perimeter And Area Class 7 Maths Chapter 11- Topics

• Squares And Rectangles
• Triangles As Parts Of Rectangles
• Area Of A Parallelogram
• Area Of A Triangle
• Circles
• Circumference Of A Circle
• Area Of a Circle

NCERT Solutions for Class 7 Maths Chapter 9 Perimeter and Area - Points to Remember

Area of a triangle: If the base length and height of a triangle are given

$Area=\frac{1}{2}\times base\times height$

The perimeter of the triangle: The perimeter will be equal to the sum of the sides of the triangle

$\text{Perimeter}=a+b+c\\$

a- First side of the triangle

b- Second side of the triangle

c- Third side of the triangle

Area of Circles:

$Area=\pi r^2$

r- Radius of the circle

Circumference of Circle:

$\text{Circumference }=2\pi r$

r- Radius of the circle

Area of a parallelogram:

$Area= b\times h$

b- base length

h- height

NCERT Solutions for Class 7 Maths Chapter Wise

NCERT Solutions for Class 7 Subject Wise

Careers360 also provides solutions for all other subjects of Class 7. These subject-wise solutions contain all the solutions for all the chapters, subject-wise. Check out the links below to access the subject-wise Class 7 solutions.

• NCERT Solutions for Class 7 Maths
• NCERT Solutions for Class 7 Science

Students can also check the NCERT Books and the NCERT Syllabus here:

• NCERT Syllabus Class 7 Maths
• NCERT Books Class 7
• NCERT Syllabus Class 7