Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 3.2 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables

NCERT Solutions for Exercise 3.2 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables

Edited By Ramraj Saini | Updated on Nov 08, 2023 08:07 PM IST | #CBSE Class 10th

NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.2

NCERT Solutions for class 10 maths ex 3.2 Pair of Linear Equations in two variables is discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. This ex 3.2 class 10 deals with the graphical and algebraic representations of linear equations in two variables and their different type of solutions such as a unique solution, no solutions or infinitely many solutions, using the five methods namely the Graphical method, substitution method, cross Multiplication method, elimination method and determinant method.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.2
  2. Download PDF of NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.2
  3. Access Exercise 3.2 Class 10 Maths Answers
  4. More About NCERT Solutions for Class 10 Maths Exercise 3.2
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 3.2
  6. NCERT Solutions of Class 10 Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 3.2 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables
NCERT Solutions for Exercise 3.2 Class 10 Maths Chapter 3 - Pair of Linear Equations in two variables

These class 10 maths ex 3.2 solutions are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Tallentex 2025 - ALLEN's Talent Encouragement Exam

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

Apply

Download PDF of NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.2

Download PDF

Access Exercise 3.2 Class 10 Maths Answers

Pair of Linear Equations in Two Variables Class 10 Chapter 3 Exercise: 3.2

Q1 Form the pair of linear equations in the following problems and find their solutions graphically.

(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

Answer:

Let the number of boys is x and the number of girls is y.

Now, According to the question,

Total number of students in the class = 10, i.e.

\Rightarrow x+y=10.....(1)

And

the number of girls is 4 more than the number of boys,i.e.

x=y+4

\Rightarrow x-y=4..........(2)

Different points (x, y) for equation (1)

X
5
6
4
Y
5
4
6

Different points (x,y) satisfying (2)

X
5
6
7
y
1
2
3


Graph,

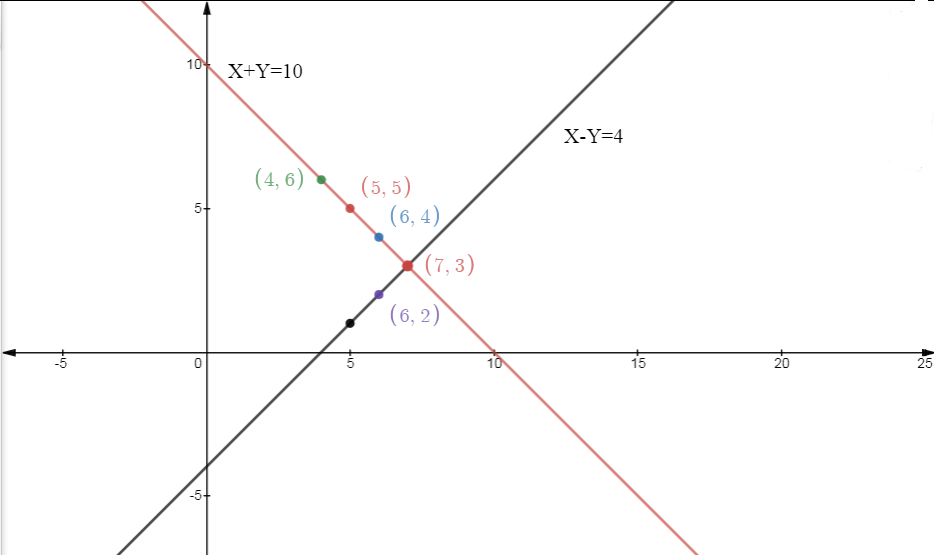
1635919752095

As we can see from the graph, both lines intersect at the point (7,3). that is x= 7 and y = 3 which means the number of boys in the class is 7 and the number of girls in the class is 3.

Q1 Form the pair of linear equations in the following problems and find their solutions graphically.

(ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and that of one pen.

Answer:

Let x be the price of 1 pencil and y be the price of 1 pen,

Now, According to the question

5x+7y=50......(1)

And

7x+5y=46......(2)

Now, the points (x,y), that satisfies the equation (1) are

X
3
-4
10
Y
5
10
0

And, the points(x,y) that satisfies the equation (2) are

X
3
8
-2
Y
5
-2
12

The Graph,

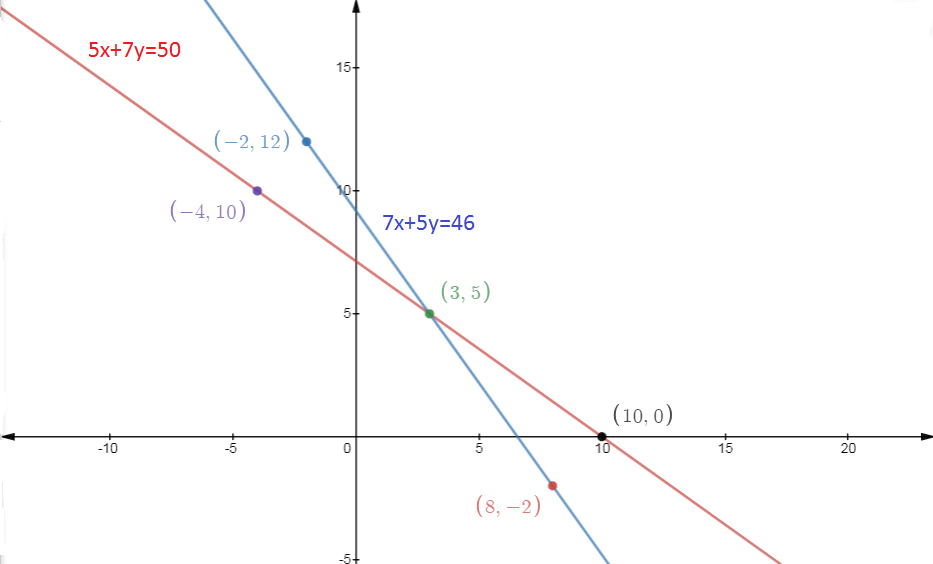
Graph

As we can see from the Graph, both line intersects at point (3,5) that is, x = 3 and y = 5 which means cost of 1 pencil is 3 and the cost of 1 pen is 5.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (i) \\5x - 4y + 8 = 0\\ 7x + 6y - 9 = 0

Answer:

Give, Equations,

\\5x - 4y + 8 = 0\\ 7x + 6y - 9 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{5}{7},\:\frac{b_1}{b_2}=\frac{-4}{6}\:and\:\frac{c_1}{c_2}=\frac{8}{-9}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means that both lines intersect at exactly one point.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (ii) \\9x + 3y + 12 = 0\\ 18x + 6y + 24 = 0

Answer:

Given, Equations,

\\9x + 3y + 12 = 0\\ 18x + 6y + 24 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}\:and \\\:\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means that both lines are coincident.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2} , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident: (iii) \\6x - 3y + 10 = 0\\ 2x - y+ 9 = 0

Answer:

Give, Equations,

\\6x - 3y + 10 = 0\\ 2x - y+ 9 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{6}{2}=3,\:\frac{b_1}{b_2}=\frac{-3}{-1}=3\:and\:\frac{c_1}{c_2}=\frac{10}{9}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means that both lines are parallel to each other.

Q2 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (i) 3x + 2y = 5;\qquad 2x - 3y = 7

Answer:

Give, Equations,

\\3x + 2y = 5;\qquad\\ 2x - 3y = 7

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\frac{a_1}{a_2}=\frac{3}{2},\:\frac{b_1}{b_2}=\frac{2}{-3}\:and\:\frac{c_1}{c_2}=\frac{5}{7}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means the given equations have exactly one solution and thus pair of linear equations is consistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (ii) 2x - 3y = 8;\qquad 4x - 6y = 9

Answer:

Given, Equations,

\\2x - 3y = 8;\qquad \\4x - 6y = 9

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-3}{-6}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{8}{9}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means the given equations have no solution and thus pair of linear equations is inconsistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (iii) \frac{3}{2}x + \frac{5}{3}y = 7;\qquad 9x -10y = 14

Answer:

Given, Equations,

\\\frac{3}{2}x + \frac{5}{3}y = 7;\qquad\\ \\ 9x -10y = 14

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{3/2}{9}=\frac{3}{18}=\frac{1}{6},\\\:\frac{b_1}{b_2}=\frac{5/3}{-10}=\frac{5}{-30}=-\frac{1}{6}\:and\\\:\frac{c_1}{c_2}=\frac{7}{14}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means the given equations have exactly one solution and thus pair of linear equations is consistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the lines representing the following pairs of linear equations are consistent, or inconsistent: (iv) 5x - 3y = 11;\qquad -10x + 6y =-22

Answer:

Given, Equations,

5x - 3y = 11;\qquad \\-10x + 6y =-22

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{5}{-10}=-\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-3}{6}=-\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{11}{-22}=-\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means the given equations have an infinite number of solutions and thus pair of linear equations is consistent.

Q3 On comparing the ratios \frac{a_1}{a_2}, \frac{b_1}{b_2}and \frac{c_1}{c_2}, find out whether the following pair of linear equations are consistent, or inconsistent (v) \frac{4}{3}x + 2y = 8; \qquad 2x + 3y = 12

Answer:

Given, Equations,

\\\frac{4}{3}x + 2y = 8; \qquad\\\\ 2x + 3y = 12

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{4/3}{2}=\frac{4}{6}=\frac{2}{3},\\\:\frac{b_1}{b_2}=\frac{2}{3}\:\:and\\\:\frac{c_1}{c_2}=\frac{8}{12}=\frac{2}{3}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means the given equations have an infinite number of solutions and thus pair of linear equations is consistent.

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (i) x + y = 5 \qquad 2x + 2 y = 10

Answer:

Given, Equations,

\\x + y = 5 \qquad\\ 2x + 2 y = 10

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{5}{10}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

It means the given equations have an infinite number of solutions and thus pair of linear equations is consistent.

The points (x,y) which satisfies in both equations are

X
1
3
5
Y
4
2
0

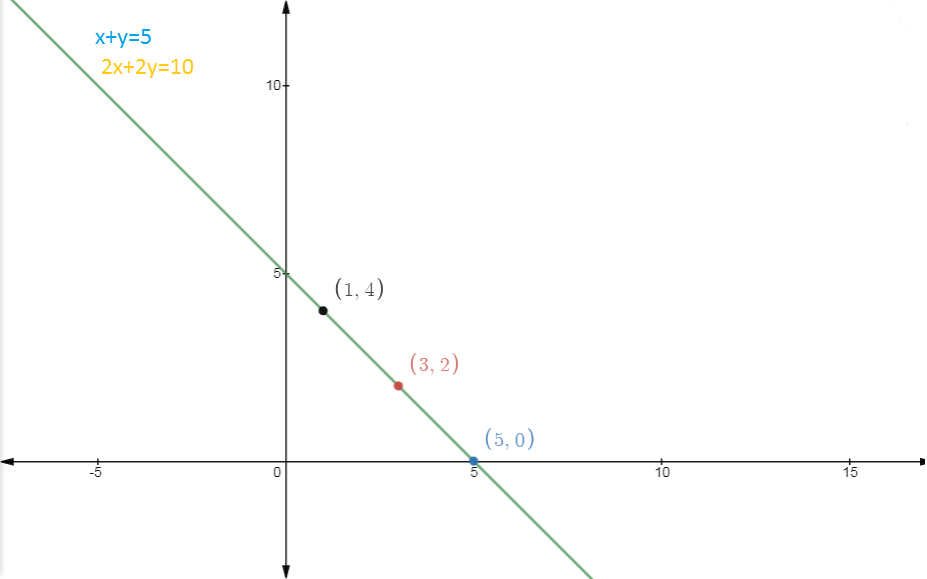
Graph

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (ii) x - y = 8,\qquad 3x - 3y = 16

Answer:

Given, Equations,

\\x - y = 8,\qquad\\ 3x - 3y = 16

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{1}{3},\\\:\frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3}\:and\\\:\frac{c_1}{c_2}=\frac{8}{16}=\frac{1}{2}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means the given equations have no solution and thus pair of linear equations is inconsistent.

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (iii) 2x + y - 6 =0, \qquad 4x - 2 y - 4 = 0

Answer:

Given, Equations,

\\2x + y - 6 =0, \qquad \\4x - 2 y - 4 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{1}{-2}=-\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{-6}{-4}=\frac{3}{2}

As we can see

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

It means the given equations have exactly one solution and thus pair of linear equations is consistent.

Now The points(x, y) satisfying the equation are,

X
0
2
3
Y
6
2
0


And The points(x,y) satisfying the equation \\4x - 2 y - 4 = 0 are,

X
0
1
2
Y
-2
0
2


GRAPH:

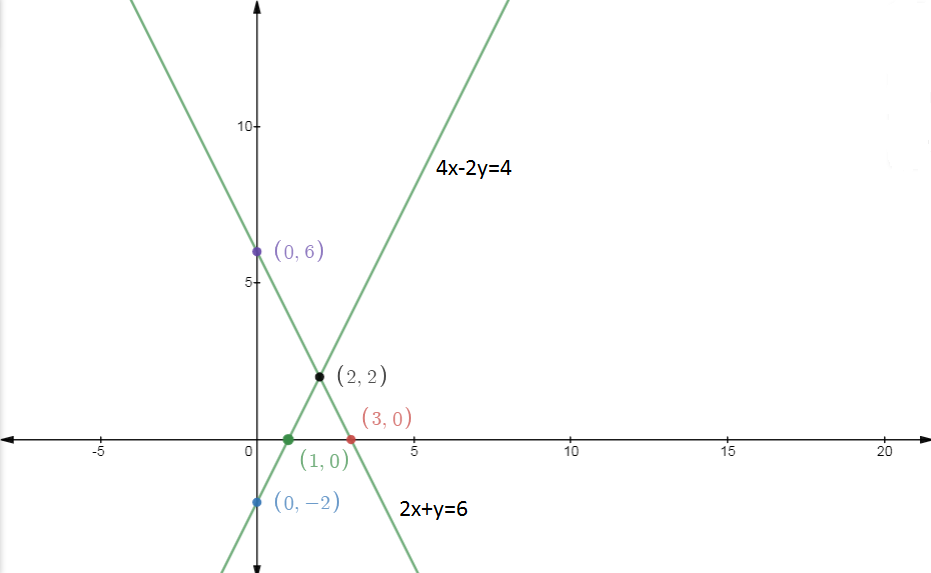
1635919975632

As we can see both lines intersects at point (2,2) and hence the solution of both equations is x = 2 and y = 2.

Q4 Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically: (iv) 2x - 2y - 2 =0, \qquad 4x - 4y -5 = 0

Answer:

Given, Equations,

\\2x - 2y - 2 =0, \qquad\\ 4x - 4y -5 = 0

Comparing these equations with a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , we get

\\\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2},\\\:\frac{b_1}{b_2}=\frac{-2}{-4}=\frac{1}{2}\:and\\\:\frac{c_1}{c_2}=\frac{-2}{-5}=\frac{2}{5}

As we can see

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

It means the given equations have no solution and thus pair of linear equations is inconsistent.

Q5 Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.

Answer:

Let lbe the length of the rectangular garden and b be the width.

Now, According to the question, the length is 4 m more than its width.i.e.

l=b+4

l-b=4....(1)

Also Given Half Parameter of the rectangle = 36 i.e.

l+b=36....(2)

Now, as we have two equations, on adding both equations, we get,

l+b+l-b=4+36

\Rightarrow 2l=40

\Rightarrow l=20

Putting this in equation (1),

\Rightarrow 20-b=4

\Rightarrow b=20-4

\Rightarrow b=16

Hence Length and width of the rectangle are 20m and 16 respectively.

Q6 Given the linear equation 2x + 3y -8 =0 , write another linear equation in two variables such that the geometrical representation of the pair so formed is: (i) intersecting lines

Answer:

Given the equation,

2x + 3y -8 =0

As we know that the condition for the intersection of lines a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , is ,

\frac{a_1}{a_2}\neq\frac{b_1}{b_2}

So Any line with this condition can be 4x+3y-16=0

Here,

\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{3}{3}=1

As

\frac{1}{2}\neq1 the line satisfies the given condition.

Q6 Given the linear equation 2x + 3y -8 =0 , write another linear equation in two variables such that the geometrical representation of the pair so formed is (ii) parallel lines

Answer:

Given the equation,

2x + 3y -8 =0

As we know that the condition for the lines a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , for being parallel is,

\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}

So Any line with this condition can be 4x+6y-8=0

Here,

\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}

\frac{c_1}{c_2}=\frac{-8}{-8}=1

As

\frac{1}{2}=\frac{1}{2}\neq1 the line satisfies the given condition.

Q6 Given the linear equation 2x + 3y -8 =0 , write another linear equation in two variables such that the geometrical representation of the pair so formed is: (iii) coincident lines

Answer:

Given the equation,

2x + 3y -8 =0

As we know that the condition for the coincidence of the lines a_1x+b_1y+c_1=0\:and\:a_2x+b_2y+c_2=0 , is,

\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}

So any line with this condition can be 4x+6y-16=0

Here,

\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}

\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}

\frac{c_1}{c_2}=\frac{-8}{-16}=\frac{1}{2}

As

\frac{1}{2}=\frac{1}{2}=\frac{1}{2} the line satisfies the given condition.

Q7 Draw the graphs of the equations x - y + 1=0and 3x +2 y - 12=0 . Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.

Answer:

Given, two equations,

x - y + 1=0.........(1)

And

3x +2 y - 12=0.........(2)

The points (x,y) satisfying (1) are

X
0
3
6
Y
1
4
7

And The points(x,y) satisfying (2) are,

X
0
2
4
Y
6
3
0


GRAPH:

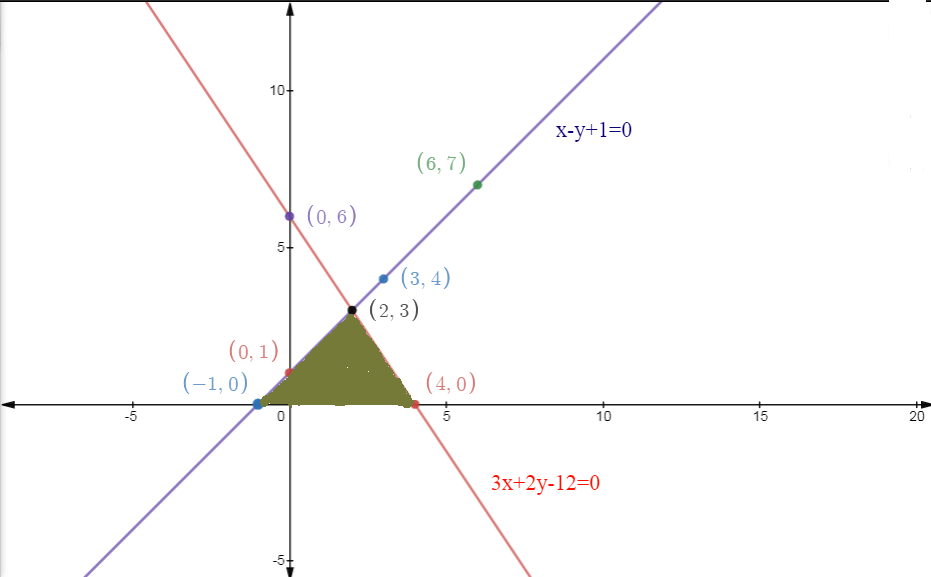
1635920037829

As we can see from the graph that both lines intersect at the point (2,3), And the vertices of the Triangle are ( -1,0), (2,3) and (4,0). The area of the triangle is shaded with a green colour.

More About NCERT Solutions for Class 10 Maths Exercise 3.2

The emphasis of NCERT solutions for Class 10 Maths exercise 3.2 was on graphical representations of linear equations in two variables, types of solutions, and associated graphs. Two systems of equations can be parallel at times. They have no solution in such situations. In rare situations, the two systems of equations may coincide, resulting in an infinite number of solutions for the given system. If the two systems of equations overlap, the given system is said to be consistent because it has a unique solution. NCERT solutions for Class 10 Maths exercise 3.2 was on the graphical depiction of the system of equations. NCERT syllabus Exercise 3.2 Class 10 Maths contains all three questions relating to the graphical depiction.Also students can get access of Pair of linear equations in two variables notes to revise all the concepts discussed in this chapter.

Benefits of NCERT Solutions for Class 10 Maths Exercise 3.2

  • NCERT solutions for Class 10 Maths exercise 3.2 help us solve and revise all of the problems in these exercises, as well as develop a deeper grasp of the pair of linear equations in two variables.
  • If you thoroughly practise the NCERT solution for Class 10th Maths chapter 3 exercise 3.2, which contains all significant questions from the exam point and all questions are revisited, you will be able to acquire higher marks in the test.
  • Exercise 3.2 Class 10 Maths, is based on graphical and algebraic representations of two-variable linear equations, types of solutions, and their graphs, all of which are significant concepts in the chapter.

Also see-

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. Check whether the equation xy - 9 = 3 a linear equation in two variables ?

The concepts related to linear equation is discussed in ex 3.2 class 10. Practice the problems discussed in this exercise to command the concepts. For this question, because of the term xy is of degree 2,  xy - 9 = 3 is not a linear equation in two variables.

2. In a graph, how many quadrants are there?

To understand the concepts of quadrants go through the problems discussed in class 10 maths ex 3.2. In a graph, there are four quadrants. a point can be represent in in a plain using the (x, y) coordinates.

3. When two lines intersect on a plane, how many choices are there, and what are they?

To get in depth understanding of related concepts practice problems enumerated in the class 10 ex 3.2.  as per these concepts, when two lines are in a plane, there are three alternative solutions. They really are. 

  • Two lines may intersect at times.
  • Two lines may not intersect at times, and they may be parallel to each other.
  • Two lines may be coincident at times.
4. In the NCERT solutions for Class 10 Maths chapter 3 exercise 3.2 How many questions and what types of questions are covered ?

In Class 10th Maths chapter 3 exercise 3.2, there are seven questions based on the notion of graphical representation of a system of equations.

5. How many solutions are there for linear equations in two variables if the equations are inconsistent and independent?

If the equations are consistent and dependent, there are no solutions to linear equations in two variables.

6. What is the criterion for two-variable linear equations that are both consistent and dependent?

You can go through the 10th class maths exercise 3.2 answers to get deeper understanding of the concepts related to equations are consistent and dependent. The requirement for linear equations in two variables is:  

a1/a2 = b1/b2 = c1/c2

7. According to NCERT solutions for Class 10 Maths chapter 3 exercise 3.2 , What is the graphical method of solution of a pair of linear equations?

The basic strategy to represent the linear equations on the graph and determine the point of intersection is the graphical method of solution of a pair of linear equations.

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:22 July,2024 - 31 August,2024

International General Knowledge Olympiad

Exam Date:19 September,2024 - 19 September,2024

Unified Cyber Olympiad

Exam Date:20 September,2024 - 20 September,2024

International English Olympiad

Exam Date:26 September,2024 - 26 September,2024

International Olympiad of Mathematics

Application Date:30 September,2024 - 30 September,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
can we apply for diploma if we have passed 10th cbse lo

Yes, you can definitely apply for diploma courses after passing 10th CBSE. In fact, there are many diploma programs designed specifically for students who have completed their 10th grade.

Generally, passing 10th CBSE with a minimum percentage (often 50%) is the basic eligibility for diploma courses. Some institutes might have specific subject requirements depending on the diploma specialization.

There is a wide range of diploma courses available in various fields like engineering (e.g., mechanical, civil, computer science), computer applications, animation, fashion design, hospitality management, and many more.

You can pursue diplomas at various institutions like:


Read Complete Answer
Nitin Kumar 14 June,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Registrations 2024
PTE Registrations 2024
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer!

JEE Main high scoring chapters and topics
JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST
CBSE Class 10 compartment result 2024 soon at cbseresults.nic.in; websites to check
August 03, 2024 - 04:38 PM IST
CBSE 10th, 12th revaluation lot 2 result 2024 out at cbseresults.nic.in; passing marks
July 30, 2024 - 06:39 PM IST
CBSE: No open book exams for Classes 10, 12 this year; pilot only in a few schools
June 12, 2024 - 10:52 AM IST
CBSE Class 10 result 2024 revaluation application begins at cbse.gov.in; apply by May 24
May 21, 2024 - 02:20 PM IST

Stay up-to date with CBSE Class 10th News

Back to top