NCERT Solutions for Class 12 Maths Chapter 12 Exercise 12.1 - Linear Programming
Linear programming involves finding the optimal value of variables that solves a certain problem. This has a wide variety of real life applications such as charting travel paths, buisness and economics, physics based problems and many more. Class 12 maths chapter 12 exercise 12.1 solutions covers graphical methods to solve linear programming problems. The chapter deals with mathematically analysing constraints and conditions to get the best possible solution to day-to-day problems.
This Story also Contains
- Class 12 Maths Chapter 12 Exercise 12.1 Solutions: Download PDF
- NCERT Solutions Class 12 Maths Chapter 12: Exercise 12.1
- Topics covered in Chapter 12 Linear Programming: Exercise 12.1
- Also see-
- NCERT Solutions Subject Wise
- Subject Wise NCERT Exemplar Solutions
NCERT solutions for exercise 12.1 Class 12 Maths gives practice questions to understand linear programming problems. These solutions of NCERT are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2025-26. The answers are designed as per the students demand covering comprehensive, step by step solutions of every problem.
Class 12 Maths Chapter 12 Exercise 12.1 Solutions: Download PDF
Students can find all exercise enumerated in NCERT Book together using the link provided below. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts.
NCERT Solutions Class 12 Maths Chapter 12: Exercise 12.1
Answer:
The region determined by constraints,
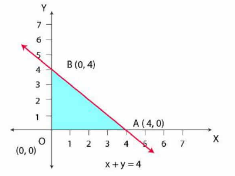
The region A0B represents the feasible region
The corner points of the feasible region are
Maximize
The value of these points at these corner points are :
Corner points | ||
12 | ||
0 | ||
16 | maximum |
The maximum value of Z is 16 at
Answer:
The region determined by constraints,
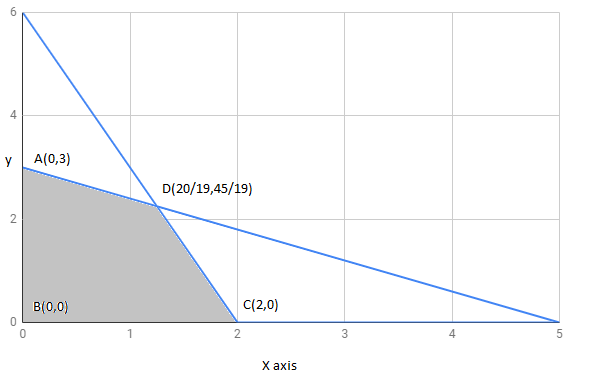
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
6 | ||
-12 | Minimum | |
0 | ||
16 |
The minimum value of Z is -12 at
Answer:
The region determined by constraints,
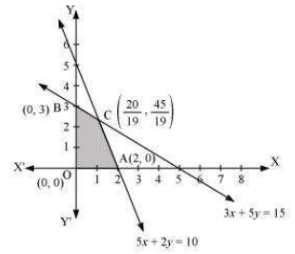
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
9 | ||
0 | ||
10 | ||
Maximum |
The maximum value of Z is
Answer:
The region determined by constraints
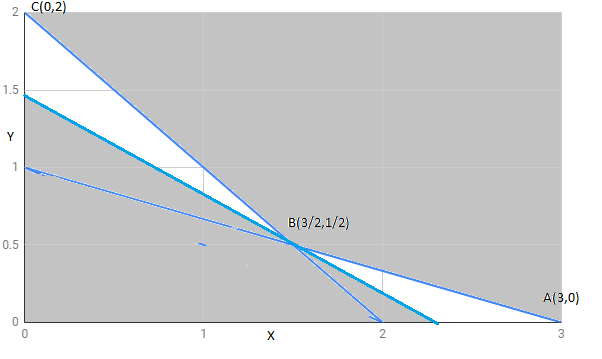
The feasible region is unbounded as shown.
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | ||
9 | ||
7 | Minimum | |
10 | ||
The feasible region is unbounded, therefore 7 may or may not be the minimum value of Z .
For this, we draw
We can see a feasible region has no common point with.
Hence, Z has a minimum value of 7 at
Answer:
The region determined by constraints,
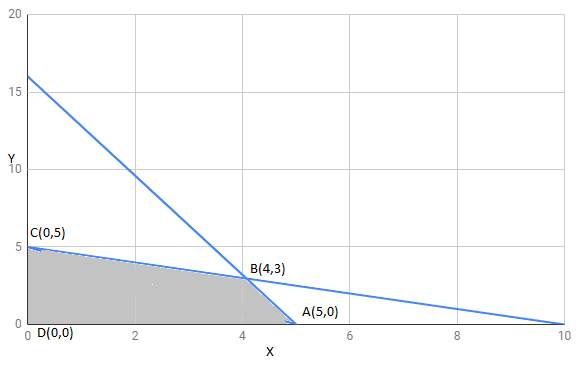
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
15 | ||
18 | Maximum | |
10 | ||
The maximum value of Z is 18 at
Question 6: Solve the following Linear Programming Problems graphically: Minimise
Show that the minimum of Z occurs at more than two points.
Answer:
The region determined by constraints
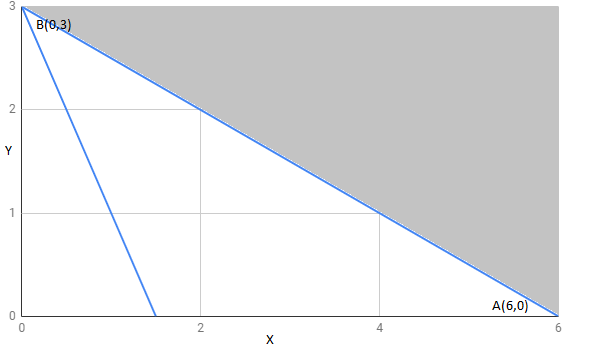
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | |
6 | |
6 |
Value of Z is the same at both points.
If we take any other point like
Thus the minimum value of Z occurs at more than 2 points .
Therefore, the value of Z is minimum at every point on the line
Answer:
The region determined by constraints,
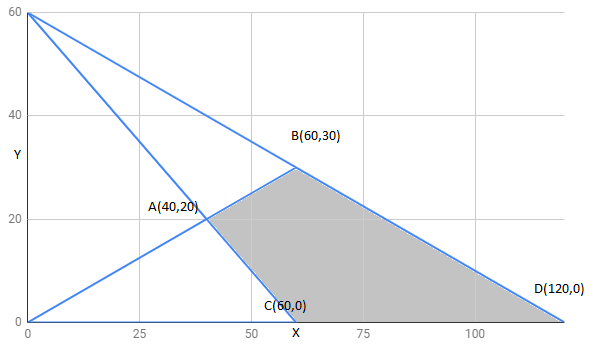
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
400 | ||
600 | Maximum | |
300 | Minimum | |
600 | maximum |
The minimum value of Z is 300 at
Answer:
The region determined by constraints
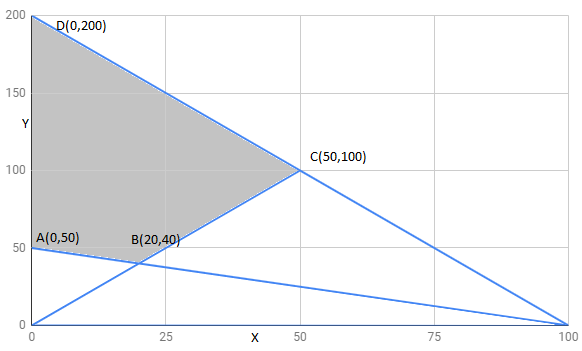
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | ||
100 | Minimum | |
100 | Minimum | |
250 | ||
400 | Maximum |
The minimum value of Z is 100 at all points on the line segment joining points
The maximum value of Z is 400 at
Answer:
The region determined by constraints
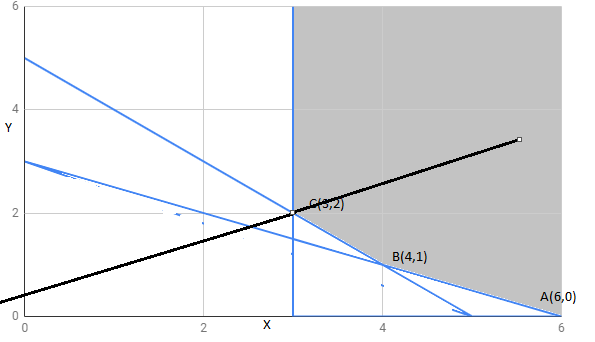
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | ||
- 6 | minimum | |
-2 | ||
1 | maximum | |
The feasible region is unbounded, therefore 1 may or may not be the maximum value of Z.
For this, we draw
We can see the resulting feasible region has a common point with a feasible region.
Hence , Z =1 is not maximum value , Z has no maximum value.
Answer:
The region determined by constraints
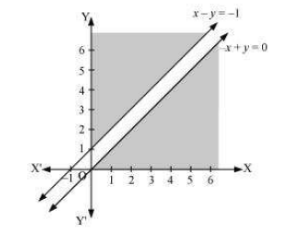
There is no feasible region and thus, Z has no maximum value.
Topics covered in Chapter 12 Linear Programming: Exercise 12.1
Linear programming is generally defined as the technique for maximising or minimising a linear function of several variables, like input or output cost. The following are some of the basic terminology used in linear programming problems.
- Objective Function: Let Z = ax + by be a linear function, where a, b are the constants. Linear objective function goes by the computation of the maximum or the minimum of X
- Decision Variables: Let Z = ax + by be a linear objective function. Then the variables x and y are called decision variables.
- Constraints: Constraints are the limitations or restrictions imposed on the decision variables.
- Optimization problem: A problem that asks to maximise or minimise a linear function limited to certain constraints.
- Optimal (feasible) solution: Any point in the feasible region that gives the maximum or minimum value of the objective function is called an optimal solution.
Theorems
- Theorem 1: Let R be the feasible region (convex polygon) for a linear programming problem and let
- Theorem 2: Let R be the feasible region for a linear programming problem, and let
Method Of Solving A Linear Problem
Find the feasible region of the problem and find the vertices.
Find the objective function Z = ax + by. Let M and m be the largest and the smallest points of the problem
When the area is bounded. "M" and "m" are maximum and minimum values. If a feasible area is unbounded then
ax + by > M, no common points with the feasible region.
- ax + by < m, no common points with the feasible region.
Also see-
NCERT Solutions Subject Wise
Subject Wise NCERT Exemplar Solutions
Frequently Asked Questions (FAQs)
For CBSE Class 12 Maths exam one question of 5 marks is expected from the chapter linear programming.
The linear programming questions will have an objective function. Either maximise or minimize the it according to the given constrains.
Graphical method is used to solve the problems in Class 12 chapter 12
There are three exercises including miscellaneous.
Ten questions are explained in the NCERT Class 12 chapter exercise 1
There are 5 solved examples before exercise 12.1
Solving NCERT exercise give more conceptual understanding and students will be able to clear their doubts and can understand the are where they have to improve.
First understand the concepts and practice solved example. Then move on to the exercise and try to solve it yourself. If you have any doubts look in to the Class 12 Maths chapter 12 exercise 12.1 solutions.
Questions related to CBSE Class 12th
On Question asked by student community
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
The CBSE Sahodaya Class 12 Pre-Board Chemistry Question Paper for the 2025-2026 session is available for download on the provided page, along with its corresponding answer key.
The Sahodaya Pre-Board exams, conducted in two rounds (Round 1 typically in December 2025 and Round 2 in January 2026), are modeled precisely
Hello,
You can get the Class 11 English Syllabus 2025-26 from the Careers360 website. This resource also provides details about exam dates, previous year papers, exam paper analysis, exam patterns, preparation tips and many more. you search in this site or you can ask question we will provide you the
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
