NCERT Solutions for Exercise 13.9 Class 9 Maths Chapter 13 - Surface Area and Volumes

Q2 The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in Fig $\small 13.32$ . Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius $\small 1.5\hspace{1mm}cm$ and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per $\small cm^2$ and black paint costs 5 paise per $\small cm^2$ .

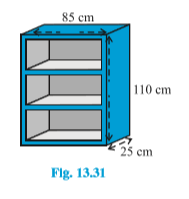
Answer:

Given,

The radius of the wooden spheres = $r_1 = \frac{21}{2}\ cm$

$\therefore$ The surface area of a single sphere = $4\pi r_1^2$

$\\ = 4\times\frac{22}{7}\times\frac{21}{2}\times\frac{21}{2} \\ = 22\times3\times21$

$= 1386\ cm^2$

Again, the Radius of the cylinder support = $\small r_2 = 1.5\hspace{1mm}cm$

Height of the support = $h = 7\ cm$

$\therefore$ The base area of the cylinder = $\pi r_2^2 = \frac{22}{7}\times1.5\times1.5 = 7.07\ cm^2$

Now, Cost of painting $1\ cm^2$ silver = $25\ paise = Rs.\ 0.25$

$\therefore$ Cost of painting 1 wooden sphere = Cost of painting $(1386-7.07)\ cm^2$ silver

= $Rs. (0.25\times1378.93) = Rs.\ 344.7325$

Now, Curved surface area of the cylindrical support = $2\pi r_2 h$

$\\ = 2\times\frac{22}{7}\times1.5\times7 \\ = 22\times3 \\ = 66\ cm^2$

Now, Cost of painting $1\ cm^2$ black = $5\ paise = Rs.\ 0.05$

$\therefore$ Cost of painting 1 such stand = Cost of painting $66\ cm^2$ silver = $Rs. (0.05\times66) = Rs.\ 3.3$

$\therefore$ The total cost of painting 1 sphere and its support = $Rs.\ (344.7325+3.3) = Rs.\ 348.0325$

Therefore, total cost of painting 8 such spheres and their supports = $Rs.\ (8\times348.0325) = Rs.\ 2784.26$

Q3 The diameter of a sphere is decreased by $\small 25\%$ . By what per cent does its curved surface area decrease?

Answer:

Let the radius of the sphere be $r$

Diameter of the sphere = $2r$

According to question,

Diameter is decreased by $\small 25\%$

So, the new diameter = $\frac{3}{4}\times2r = \frac{3r}{2}$

So, the new radius = $r' = \frac{3r}{4}$

$\therefore$ New surface area = $4\pi r'^2 = 4\pi (\frac{3r}{4})^2$

$\therefore$ Decrease in surface area = $4\pi r^2 - 4\pi (\frac{3r}{4})^2$

$= 4\pi r^2[1 -\frac{9}{16} ]$

$= 4\pi r^2[\frac{7}{16} ]$

$\therefore$ Percentage decrease in the surface area = $\frac{Difference\ in\ areas}{Original\ surface\ area}$

$= \frac{4\pi r^2[\frac{7}{16}]}{4\pi r^2}\times100 \%$

$= \frac{7}{16}\times100 \%$

$= 43.75 \%$