NCERT Solutions for Exercise 13.1 Class 9 Maths Chapter 13 - Surface Area and Volumes

Q1 (i) A plastic box $\small 1.5\hspace {1mm}m$ long, $\small 1.25\hspace {1mm}m$ wide and $\small 65\hspace {1mm}cm$ deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine: The area of the sheet required for making the box.

Answer:

Given, dimensions of the plastic box

Length, $l = 1.5\ m$

Width, $b = 1.25\ m$

Depth, $h = 65\ cm = 0.65\ m$

(i) The area of the sheet required for making the box (open at the top)= Lateral surface area of the box. + Area of the base.

= $2(bh+hl)+lb$

$\\ = 2(1.25\times0.65+0.65\times1.5)+1.5\times1.25 \\ = 2(0.8125+ 0.975)+1.875= 5.45$

The required area of the sheet required for making the box is $5.45\ m^2$

Q1 (ii) A plastic box $\small 1.5\hspace {1mm} m$ long, $\small 1.25\hspace {1mm} m$ wide and $\small 65\hspace {1mm} cm$ deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine: The cost of sheet for it, if a sheet measuring $\small 1m^2$ costs Rs 20.

Answer:

Given, dimensions of the plastic box

Length, $l = 1.5\ m$

Width, $b = 1.25\ m$

Depth, $h = 65\ cm = 0.65\ m$

We know, area of the sheet required for making the box is $5.45\ m^2$

(ii) Cost for $\small 1m^2$ of sheet = Rs 20

$\therefore$ Cost for $5.45\ m^2$ of sheet = $5.45\times20 = 109$

Required cost of the sheet is $Rs.\ 109$

Q2 The length, breadth and height of a room are $\small 5\hspace {1mm}m$ , $\small 4\hspace {1mm}m$ and $\small 3\hspace {1mm}m$ respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of $\small Rs \hspace {1mm} 7.50$ per $\small m^2$ .

Answer:

Given,

Dimensions of the room = $5\ m\times4\ m\times3\ m$

Required area to be whitewashed = Area of the walls + Area of the ceiling

= $2(lh+bh) + lb$

$\\ = 2(5\times4+4\times3)+ 5\times4 \\ = 2(32)+20 = 74\ m^2$
Cost of white-washing per $\small m^2$ area = $\small Rs \hspace {1mm} 7.50$
Cost of white-washing $74\ m^2$ area = $Rs (74 \times 7.50)$
$= Rs.\ 555$

Therefore, the required cost of whitewashing the walls of the room and the ceiling is $Rs.\ 555$

Q3 The floor of a rectangular hall has a perimeter $\small 250\hspace {1mm} m$ . If the cost of painting the four walls at the rate of Rs 10 per $\small m^2$ is Rs 15000, find the height of the hall. [ Hint : Area of the four walls $\small =$ Lateral surface area.]

Answer:

Given,

The perimeter of rectangular hall = $\small 250\hspace {1mm} m$

Cost of painting the four walls at the rate of Rs 10 per $\small m^2$ = Rs 15000

Let the height of the wall be $h\ m$

$\therefore$ Area to be painted = $Perimeter\times height$

$= 250h\ m^2$

$\therefore$ Required cost = $250h\times10\ m^2 = 15000\ m^2$

$\\ \implies 2500h = 15000 \\ \implies h = \frac{150}{25} = 6\ m$

Therefore, the height of the hall is $6\ m$

Q4 The paint in a certain container is sufficient to paint an area equal to $\small 9.375\hspace{1mm} m^2$ . How many bricks of dimensions $\small 22.5\hspace {1mm}cm \times 10\hspace {1mm}cm \times 7.5\hspace {1mm}cm$ can be painted out of this container?

Answer:

Given, dimensions of the brick = $\small 22.5\hspace {1mm}cm \times 10\hspace {1mm}cm \times 7.5\hspace {1mm}cm$

We know, Surface area of a cuboid = $2(lb+bh+hl)$

$\therefore$ The surface area of a single brick = $2(22.5\times10+10\times7.5+7.5\times22.5)$

$= 2(225+75+166.75) = 937.5\ cm^2 = 0.09375\ m^2$

$\therefore$ Number of bricks that can be painted = $\frac{Total\ area\ the\ container\ can\ paint}{Surface\ area\ of\ a\ single\ brick}$

$= \frac{9.375}{0.09375} = 100$

Therefore, the required number of bricks that can be painted = 100

Q5 (i) A cubical box has each edge $\small 10 \hspace{1mm}cm$ and another cuboidal box is $\small 12.5 \hspace{1mm}cm$ long, $\small 10 \hspace{1mm}cm$ wide and $\small 8 \hspace{1mm}cm$ high.

Which box has the greater lateral surface area and by how much?

Answer:

Given,

Edge of the cubical box =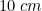

Dimensions of the cuboid =

(ii) The total surface area of the cubical box =

The total surface area of the cuboidal box =

Clearly, the total surface area of a cuboidal box is greater than the cubical box.

Difference between them =

Q5 (ii) A cubical box has each edge $\small 10 \hspace {1mm}cm$ and another cuboidal box is $\small 12.5 \hspace {1mm}cm$ long, $\small 10 \hspace {1mm}cm$ wide and $\small 8 \hspace {1mm}cm$ high.

Which box has the smaller total surface area and by how much?

Answer:

Given,

Edge of the cubical box =

Dimensions of the cuboid =

(ii) The total surface area of the cubical box =

The total surface area of the cuboidal box =

Clearly, the total surface area of a cuboidal box is greater than the cubical box.

Difference between them =

Q6 (i) A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is $\small 30 \hspace{1mm}cm$ long, $\small 25 \hspace{1mm}cm$ wide and $\small 25 \hspace{1mm}cm$ high.What is the area of the glass?

Answer:

Given, dimensions of the greenhouse = $30\ cm \times25\ cm \times25\ cm$

Area of the glass = $2[lb + lh + bh]$
$\\ = [2(30 \times 25 + 30 \times 25 + 25 \times 25)] \\ = [2(750 + 750 + 625)] \\ = (2 \times 2125) \\ = 4250\ cm^2$
Therefore, the area of glass is $4250\ cm^2$

Q6 (ii) A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high. How much of tape is needed for all the 12 edges?

Answer:

Given, dimensions of the greenhouse = $30\ cm \times25\ cm \times25\ cm$

(ii) Tape needed for all the 12 edges = Perimeter = $4(l+b+h)$

$4(30+25+25) = 320\ cm$

Therefore, $320\ cm$ of tape is needed for the edges.

Q7 Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions $\small 25\hspace {1mm}cm \times 20\hspace {1mm}cm \times 5 \hspace {1mm}cm$ , and the smaller of dimensions $\small 15\hspace {1mm}cm \times 12\hspace {1mm}cm \times 5 \hspace {1mm}cm$ . For all the overlaps, $\small 5\%$ of the total surface area is required extra. If the cost of the cardboard is Rs 4 for $\small 1000\hspace {1mm}cm^2$ , find the cost of cardboard required for supplying 250 boxes of each kind.

Answer:

Given,

Dimensions of the bigger box = $\small 25\hspace {1mm}cm \times 20\hspace {1mm}cm \times 5 \hspace {1mm}cm$ ,

Dimensions of smaller box = $\small 15\hspace {1mm}cm \times 12\hspace {1mm}cm \times 5 \hspace {1mm}cm$

We know,

Total surface area of a cuboid = $2(lb+bh+hl)$

$\therefore$ Total surface area of the bigger box = $2(25\times20+20\times5+5\times25)$

$= 2(500+100+125) = 1450\ cm^2$

$\therefore$ Area of the overlap for the bigger box = $5\%\ of\ 1450\ cm^2 = \frac{5}{100}\times1450 = 72.5\ cm^2$

Similarly,

Total surface area of the smaller box = $2(15\times12+12\times5+5\times15)$

$= 2(180+60+75) = 630\ cm^2$

$\therefore$ Area of the overlap for the smaller box = $5\%\ of\ 630\ cm^2 = \frac{5}{100}\times630 = 31.5\ cm^2$

Since, 250 of each box is required,

$\therefore$ Total area of carboard required = $250[(1450+72.5)+(630 + 31.5)] = 546000\ cm^2$

Cost of $\small 1000\hspace {1mm}cm^2$ of the cardboard = Rs 4

$\therefore$ Cost of $\small 546000\hspace {1mm}cm^2$ of the cardboard = $\small Rs. (\frac{4}{1000}\times546000) = Rs. 2184$

Therefore, the cost of the cardboard sheet required for 250 such boxes of each kind is $\small Rs.\ 2184$

Q8 Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height $\small 2.5\hspace {1mm}m$ , with base dimensions $\small 4\hspace {1mm}m\times 3\hspace {1mm}m$ ?

Answer:

Given, Dimensions of the tarpaulin = $4\ m\times 3\ m \times2.5\ m$

The required amount of tarpaulin = Lateral surface area of the shelter + Area of top

= $2(lh + bh )+ lb$ Required

$\\ = 2(4\times2.5 + 3\times2.5 )+ 4\times3 \\ = 2(10+7.5) + 12 = 47\ m^2$

Therefore, $47\ m^2$ tarpaulin is required.