NCERT Solutions for Exercise 13.7 Class 9 Maths Chapter 13

NCERT Solutions for Exercise 13.7 Class 9 Maths Chapter 13 - Surface Area and Volumes

Edited By Vishal kumar | Updated on Oct 17, 2023 09:35 AM IST

NCERT Solutions for Class 9 Maths Exercise 13.7 Chapter 13 Surface Areas and Volumes- Download Free PDF

The concept of volume of the right circular cone is discussed in NCERT Solutions for Class 9 Maths exercise 13.7. Cone is a three-dimensional form that narrows smoothly from a flat base to a point. There are two types of cones in mathematics: right circular cones and oblique cones. A right circular cone is a form of cone whose axis is perpendicular to the plane of the base, as shown in exercise 13.7 Class 9 Maths. The space or the capacity of the cone is known as the volume of the cone. The Pythagoras Theorem defines slant height as the distance between the vertex or apex and a point on the outer line of the circular base of the cone. The formula l²=r²+h² is used to calculate the slant height of a right circular cone. The volume of the right circular cone can be estimated using the right circular cone's dimensions, such as its radius and height.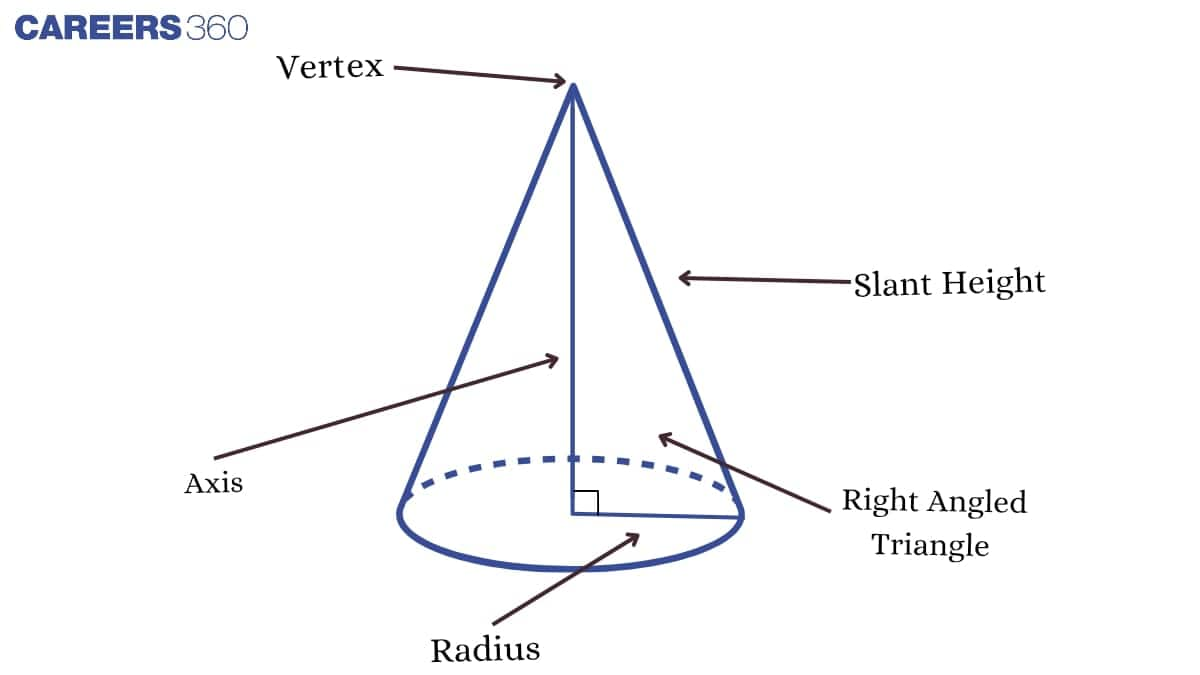

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions for Class 9 Maths Exercise 13.7 Chapter 13 Surface Areas and Volumes- Download Free PDF
Download the PDF of NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Exercise 13.7
Access Surface Area and Volumes Class 9 Maths Chapter 13 Exercise: 13.7
More About NCERT Solutions for Class 9 Maths Exercise 13.7
Benefits of NCERT Solutions for Class 9 Maths Exercise 13.7
Key Features of NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volume Exercise 13.7
NCERT Solutions of Class 10 Subject Wise

NCERT Solutions for Exercise 13.7 Class 9 Maths Chapter 13 - Surface Area and Volumes

The volume of the right circular cone is the subject of nine questions in NCERT solutions for NCERT book Class 9 Maths chapter 13 exercise 13.7. The 9th class maths exercise 13.7 answers are thoughtfully created by subject experts from Careers360. They are presented in a straightforward and detailed manner, making complex geometry concepts easy to understand. Additionally, these class 9 maths chapter 13 exercise 13.7 solutions are available in PDF format, enabling students to access them offline for completing assignments and homework with ease. The following tasks are included along with NCERT syllabus class 9 Maths chapter 13 exercise 13.7 .

**According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 11.

Download the PDF of NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Exercise 13.7

Download PDF

Access Surface Area and Volumes Class 9 Maths Chapter 13 Exercise: 13.7

Q1 (i) Find the volume of the right circular cone with radius 6 cm, height 7 cm

Answer:

Given,

Radius = $r =6\ cm$

Height = $h =7\ cm$

We know,

Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ Required volume = $\frac{1}{3}\times\frac{22}{7}\times6^2\times7$

$\\ = 22\times2\times6 \\ = 264\ cm^3$

Q1 (ii) Find the volume of the right circular cone with: radius $\small 3.5$ cm, height 12 cm

Answer:

Given,

Radius = $r =3.5\ cm$

Height = $h =12\ cm$

We know,

Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ Required volume = $\frac{1}{3}\times\frac{22}{7}\times3.5^2\times12$

$\\ = 22\times0.5\times3.5\times4 \\ = 11\times14 \\ = 154\ cm^3$

Q2 (i) Find the capacity in litres of a conical vessel with radius 7 cm, slant height 25 cm

Answer:

Given,

Radius = $r =7\ cm$

Slant height = $l = \sqrt{r^2 + h^2} = 25\ cm$

Height = $h =\sqrt{l^2-r^2} = \sqrt{25^2-7^2}$

$= \sqrt{(25-7)(25+7)} = \sqrt{(18)(32)}$

$= 24\ cm$

We know,
Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ Volume of the vessel= $\frac{1}{3}\times\frac{22}{7}\times7^2\times24$

$\\ = 22\times7\times8\\ = 154\times8 \\ = 1232\ cm^3$

$\therefore$ Required capacity of the vessel =

$= \frac{1232}{1000} = 1.232\ litres$

Q2 (ii) Find the capacity in litres of a conical vessel with height 12 cm, slant height 13 cm

Answer:

Given,

Height = $h =12\ cm$

Slant height = $l = \sqrt{r^2 + h^2} = 13\ cm$

Radius = $r =\sqrt{l^2-h^2} = \sqrt{13^2-12^2}$

$= \sqrt{(13-12)(13+12)} = \sqrt{(1)(25)}$

$= 5\ cm$

We know,
Volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ Volume of the vessel= $\frac{1}{3}\times\frac{22}{7}\times5^2\times12$

$\\ = \frac{22}{7}\times25\times4\\ = \frac{2200}{7}\ cm^3$

$\therefore$ Required capacity of the vessel =

$= \frac{2200}{7\times1000} = \frac{11}{35}\ litres$

Q3 The height of a cone is 15 cm. If its volume is 1570 $\small cm^3$ , find the radius of the base. (Use $\small \pi =3.14$ )

Answer:

Given,

Height of the cone = $h =15\ cm$

Let the radius of the base of the cone be $r\ cm$

We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ $\frac{1}{3}\times3.14\times r^2\times15 = 1570$

$\\ \Rightarrow 3.14\times r^2\times5 = 1570 \\ \Rightarrow r^2 = \frac{1570}{15.7} \\ \Rightarrow r^2 = 100 \\ \Rightarrow r = 10\ cm$

Q4 If the volume of a right circular cone of height 9 cm is $\small 48\pi \hspace{1mm}cm^3$ , find the diameter of its base.

Answer:

Given,

Height of the cone = $h =9\ cm$

Let the radius of the base of the cone be $r\ cm$

We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ $\frac{1}{3}\times\pi\times r^2\times9 = 48\pi$

$\\ \Rightarrow 3r^2 = 48 \\ \Rightarrow r^2 = 16\\ \Rightarrow r = 4\ cm$

Therefore the diameter of the right circular cone is $8\ cm$

Q5 A conical pit of top diameter $\small 3.5$ m is 12 m deep. What is its capacity in kilolitres?

Answer:

Given,

Depth of the conical pit = $h =12\ m$

The top radius of the conical pit = $r = \frac{3.5}{2}\ m$

We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ The volume of the conical pit =

$= \frac{1}{3}\times\frac{22}{7}\times \left (\frac{3.5}{2} \right )^2\times12$

$\\ = \frac{1}{3}\times\frac{22}{7}\times \frac{3.5\times 3.5}{4}\times12 \\ \\ = 22\times 0.5\times 3.5 \\ = 38.5\ m^3$

Now, $1\ m^3 = 1\ kilolitre$

$\therefore$ The capacity of the pit = $38.5\ kilolitre$

Q6 (i) The volume of a right circular cone is $\small 9856\hspace{1mm}cm^3$ . If the diameter of the base is 28 cm, find height of the cone

Answer:

Given, a right circular cone.

The radius of the base of the cone = $r = \frac{28}{2} = 14\ cm$

The volume of the cone = $\small 9856\hspace{1mm}cm^3$

(i) Let the height of the cone be $h\ m$

We know,
The volume of a right circular cone = $\frac{1}{3}\pi r^2 h$

$\therefore$ $\frac{1}{3}\times\frac{22}{7}\times(14)^2\times h = 9856$

$\\ \Rightarrow \frac{1}{3}\times\frac{22}{7}\times14\times14\times h = 9856 \\ \Rightarrow \frac{1}{3}\times22\times2\times14\times h = 9856 \\ \Rightarrow h = \frac{9856\times3}{22\times2\times14} \\ \\ \Rightarrow h =48\ cm$

Therefore, the height of the cone is $48\ cm$

Q6 (ii) The volume of a right circular cone is $\small 9856\hspace{1mm}cm^3$ . If the diameter of the base is 28 cm, find slant height of the cone

Answer:

Given, a right circular cone.

The volume of the cone = $\small 9856\hspace{1mm}cm^3$

The radius of the base of the cone = $r = \frac{28}{2} = 14\ cm$

And the height of the cone = $h = 48\ cm$

(ii) We know, Slant height, $l = \sqrt{r^2+h^2}$

$\\ \Rightarrow l = \sqrt{14^2+48^2} \\ \Rightarrow l = \sqrt{196+2304} = \sqrt{2500} \\ \Rightarrow l = 50\ cm$

Therefore, the slant height of the cone is $50\ cm$ .

Q7 (iii) The volume of a right circular cone is $\small 9856\hspace{1mm}cm^3$ . If the diameter of the base is 28 cm, find curved surface area of the cone

Answer:

Given, a right circular cone.

The radius of the base of the cone = $r = \frac{28}{2} = 14\ cm$

And Slant height of the cone = $l = 50\ cm$

(iii) We know,

The curved surface area of a cone = $\pi r l$

$\therefore$ Required curved surface area= $\frac{22}{7}\times14\times50$

$\\ = 22\times2\times50 \\ = 2200\ cm^2$

Q7 A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.

Answer:

When a right-angled triangle is revolved about the perpendicular side, a cone is formed whose,

Height of the cone = Length of the axis= $h = 12\ cm$

Base radius of the cone = $r = 5\ cm$

And, Slant height of the cone = $l = 13\ cm$

We know,

The volume of a cone = $\frac{1}{3}\pi r^2 h$

The required volume of the cone formed = $\frac{1}{3}\times\pi\times5^2\times12$

$\\ = \pi\times25\times4 \\ = 100\pi\ cm^3$

Therefore, the volume of the solid cone obtained is $100\pi\ cm^3$

Q8 If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.

Answer:

When a right-angled triangle is revolved about the perpendicular side, a cone is formed whose,

Height of the cone = Length of the axis= $h = 5\ cm$

Base radius of the cone = $r = 12\ cm$

And, Slant height of the cone = $l = 13\ cm$

We know,

The volume of a cone = $\frac{1}{3}\pi r^2 h$

The required volume of the cone formed = $\frac{1}{3}\times\frac{22}{7}\times12^2\times5$

$\\ = \pi\times4\times60 \\ = 240\pi\ cm^3$

Now, Ratio of the volumes of the two solids = $\\ = \frac{100\pi}{240\pi}$

$\\ = \frac{5}{12}$

Therefore, the required ratio is $5:12$

Q9 A heap of wheat is in the form of a cone whose diameter is $\small 10.5$ m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.

Answer:

Given,

Height of the conical heap = $h = 3\ m$

Base radius of the cone = $r = \frac{10.5}{2}\ m$

We know,

The volume of a cone = $\frac{1}{3}\pi r^2 h$

The required volume of the cone formed = $\frac{1}{3}\times\frac{22}{7}\times\left (\frac{10.5}{2} \right )^2\times3$

$\\ = 22\times\frac{1.5\times10.5}{4} \\ = 86.625\ m^3$

Now,

The slant height of the cone = $l = \sqrt{r^2+h^2}$

$\\ \Rightarrow l = \sqrt{3^2+5.25^2} = \sqrt{9+27.5625} \approx 6.05$

We know, the curved surface area of a cone = $\pi r l$

The required area of the canvas to cover the heap = $\frac{22}{7}\times\frac{10.5}{2}\times6.05$

$= 99.825\ m^2$

Benefits of NCERT Solutions for Class 9 Maths Exercise 13.7

• The solved example before the exercise 13.7 Class 10 Maths and the NCERT solutions for Class 9 Maths exercise 13.7 are crucial since they cover questions about the volume of the right circular cone.

• If students can answer all of the questions in exercise 13.7 Class 10 Maths they will be able to grasp the hit-or-miss cone concept as well as the notion of finding the proper circular cone as described in Class 9 Maths chapter 13 exercise 13.7

• For Class 9 final exams, students may receive either short or lengthy answer questions from the types discussed inclass 9 maths ex 13.7.

Key Features of NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volume Exercise 13.7

Comprehensive Coverage: Exercise 13.7 class 9 maths covers a wide range of problems related to surface areas and volumes, ensuring students have a thorough understanding of the concepts.
Expert-Crafted Solutions: The 9th class maths exercise 13.7 answers are expertly crafted to provide step-by-step explanations, making it easier for students to grasp complex topics.
Alignment with CBSE Syllabus: The class 9 maths ex 13.7 solutions adhere to the CBSE syllabus, making them an ideal resource for homework, assignments, and exam preparation.
PDF Format: Class 9 ex 13.7 solutions are available in PDF format, allowing students to access and download them for offline use, ensuring accessibility and convenience.

Also See:

NCERT Solutions of Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. The slant height of a right circular cone is _________

The slant height of a right circular cone is l^2=r^2+h^2.

2. The volume of the right circular cone is ________

The volume of the right circular cone is pi r^2 h/3

3. The cube's volume is calculated using _______ units.

Cubic units are used to measure the volume of the cube

4. Funnel is a _______ a)Cylinder b)Cone c)Sphere

Funnel is a cone. Option (b) cone.

5. Define slant height.

The Pythagoras Theorem defines slant height as the distance between the vertex or apex and a point on the outer line of the circular base of the cone.

6. According to NCERT solutions for Class 9 Maths chapter 13 exercise 13.7 , what are the types of cones?

Mathematically, There are two types of cones in ,

right circular cones
oblique cones.

7. According to NCERT solutions for Class 9 Maths chapter 13 exercise 13.4 , whether the volume of a regular cone or right circular cone and the oblique cone is the same?

Yes, The formula for the volume of a regular cone or right circular cone and the oblique cone is the same.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

BHU School Eligibility 2025: Admission Criteria for Class 6, 9 & 11

Jan 11, 2025

SoSE Delhi School Admission Eligibility Criteria 2025: Requirements & Guidelines

Jan 10, 2025

MGGS School Admission Form 2025: Apply Online for Admission

Jan 10, 2025

Dental Courses after 12th - Eligibility Criteria & Top Institutes

Jan 10, 2025

Jamia Millia Islamia School Class 9 Admissions 2025 - Know Details of Application Process, Eligibility, Fees

Jan 10, 2025

BHU School Entrance Test Admit Card 2025 - Download Class 9, 11 SET Admit Card @ bhuonline.in

Jan 10, 2025

Silverzone STEM Result 2024-25 – Check STEM Olympiad Results Online

Jan 10, 2025

Silverzone ABHO Result 2024-25 - Check Akhil Bhartiya Hindi Olympiad Results Here

Jan 10, 2025

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:18 December,2024 - 30 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:18 December,2024 - 30 January,2025

Admit Card

Result

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Exam Pattern

Answer Key

Result

Manipur Board 12th Examination

Admit Card Date:30 December,2024 - 26 March,2025

Exam Pattern

Admit Card

Result

National Means Cum-Merit Scholarship

Application Date:31 December,2024 - 24 January,2025

Eligibility Criteria

Application Process

Exam Pattern

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is