ALLEN Coaching
ApplyRegister for ALLEN Scholarship Test & get up to 90% Scholarship
A circle is a geometrical closed figure whose every point is at an equal distance from the point, called centre of the circle. The sphere is a round shape figure, or in other words sphere is a three-dimensional circle. The distance between the centre and the point that lies at the boundary or the circumference of the sphere is called the radius. The diameter of the sphere is given by 2r, where r is the radius of the sphere. The total area covered by the surface of a sphere in a three-dimensional space is known as the surface area of the sphere. The amount of space occupied by the sphere is known as the volume of the sphere, and half of the sphere is called a Hemisphere.

Class 9th maths exercise 11.2 answers are a significant component of Chapter 11. It consists of nine questions, each with multiple parts. The NCERT solutions have been meticulously crafted by subject matter experts from Careers360, ensuring they are presented in simple and detailed language for enhanced understanding. Furthermore, students can conveniently access the PDF version of these class 9 maths chapter 11 exercise 11.2 solutions, allowing them to study offline at their convenience without the need for an internet connection. The nine questions in Class 9 Maths Chapter 11 Exercise 11.2 are based on the notion of surface areas and volumes of spheres as per the NCERT Books. Class 9 Maths chapter 11 exercise 11.2 thoroughly explains the concepts of surface area and volume.
**As per the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 11.
Q1 (i) Find the surface area of a sphere of radius:
Answer:
We know,
The surface area of a sphere of radius
Q1 (ii) Find the surface area of a sphere of radius:
Answer:
We know,
The surface area of a sphere of radius
Q1 (iii) Find the surface area of a sphere of radius:
Answer:
We know,
The surface area of a sphere of radius
Q2 (i) Find the surface area of a sphere of diameter: 14 cm
Answer:
Given,
The diameter of the sphere =
We know,
The surface area of a sphere of radius
Q2 (ii) Find the surface area of a sphere of diameter: 21 cm
Answer:
Given,
The diameter of the sphere =
We know,
The surface area of a sphere of radius
Q2 (iii) Find the surface area of a sphere of diameter:
Answer:
Given,
The diameter of the sphere =
We know,
The surface area of a sphere of radius
Q3 Find the total surface area of a hemisphere of radius 10 cm. (Use
Answer:
We know,
The total surface area of a hemisphere = Curved surface area of hemisphere + Area of the circular end
Answer:
Given,
We know,
The surface area of a sphere of radius
Therefore, the required ratio is
Answer:
Given,
The inner radius of the hemispherical bowl =
We know,
The curved surface area of a hemisphere =
Now,
Cost of tin-plating
Therefore, the cost of tin-plating it on the inside is
Q6 Find the radius of a sphere whose surface area is
Answer:
Given,
The surface area of the sphere =
We know,
The surface area of a sphere of radius
Therefore, the radius of the sphere is
Answer:
Let diameter of Moon be
We know,
The surface area of a sphere of radius
Therefore, the ratio of the surface areas of the moon and earth is
Answer:
Given,
The inner radius of the bowl =
The thickness of the bowl =
We know, Curved surface area of a hemisphere of radius
Therefore, the outer curved surface area of the bowl is
Answer:
Given,
The radius of the sphere =
Answer:
Given,
The radius of the sphere = r
\thereforeThe surface area of the sphere =
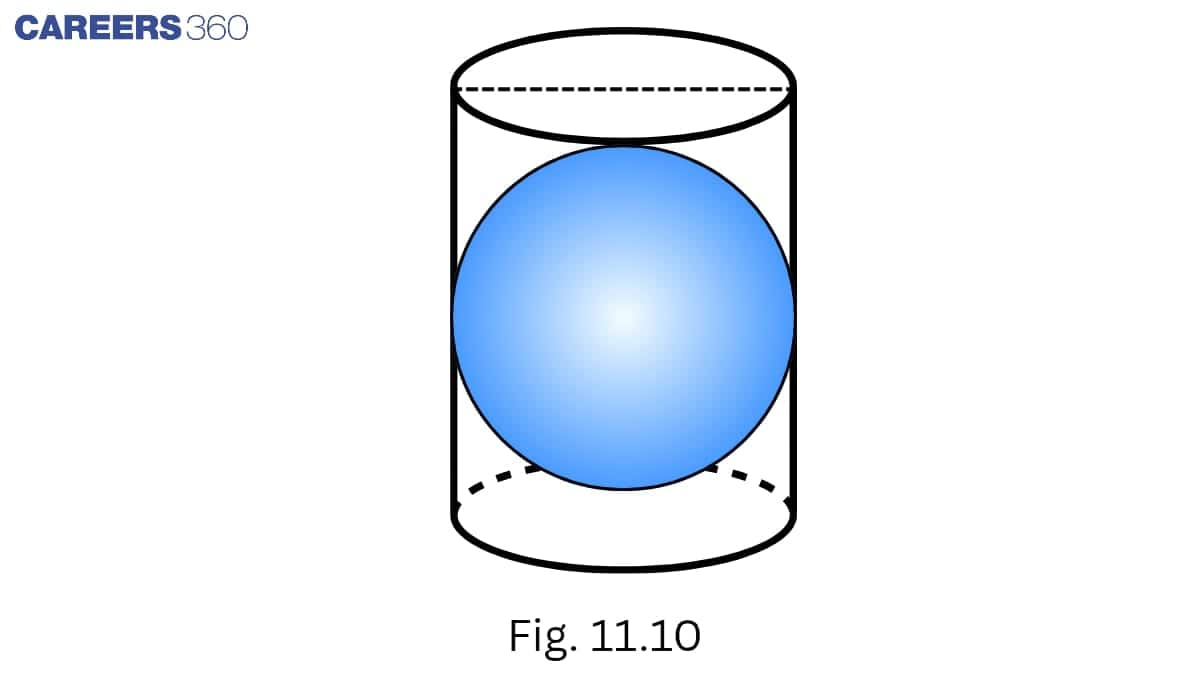
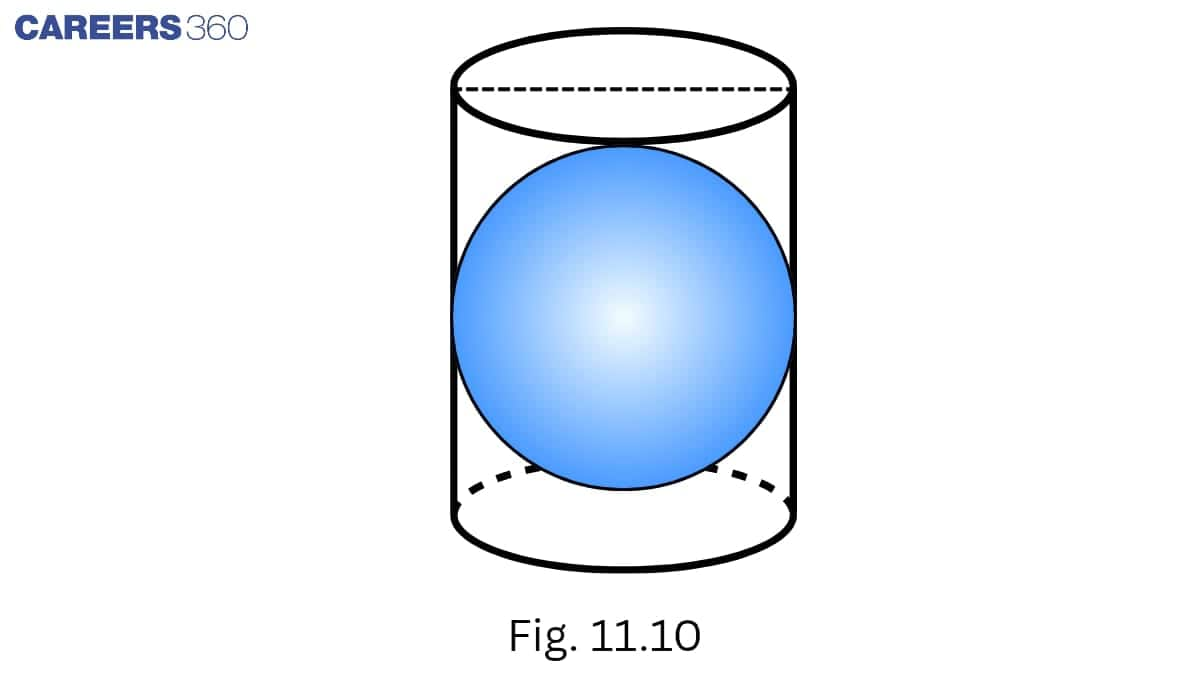
According to the question, the cylinder encloses the sphere.
Hence, the diameter of the sphere is the diameter of the cylinder.
Also, the height of the cylinder is equal to the diameter of the sphere.
We know, the curved surface area of a cylinder =
=
Therefore, the curved surface area of the cylinder is
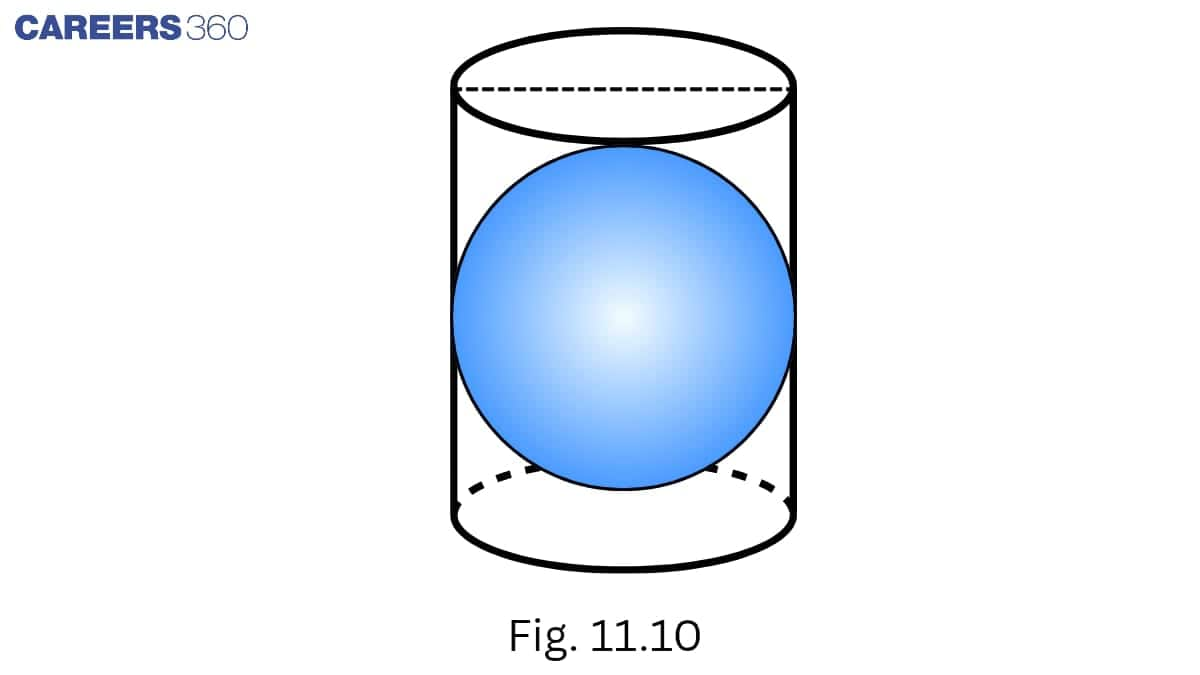
Answer:
The surface area of the sphere =
And, Surface area of the cylinder =
So, the ratio of the areas =
Also Read:
The NCERT solutions for Class 9 Maths exercise 11.2 are mainly focused on the surface area and the volume of the sphere. The surface area of the sphere is calculated by the product of four times the area of the circle.
The total surface area of the hemisphere is equal to
Also See:
Students must check the NCERT solutions for Class 9 Maths and Science given below:
Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:
A three-dimensional object with a round shape is called a sphere, according to NCERT solutions for Class 9 Maths chapter 13 exercise 13.4 .
Radius is the distance between surface and centre of the sphere whereas the diameter is the distance from one point to another point on the surface of the sphere, passing through the centre.
The sphere has a surface area of 4πr^2 .
Surface area can be divided into two categories. They are.
Area of Lateral Surface
Area of Total Surface
The total surface area of hemisphere is 3πr^2
The Lateral surface area of hemisphere is 2πr^2 .
According to NCERT solutions for Class 9 Maths chapter 13 exercise 13.4 , When a sphere is cut at the exact centre along its diameter which leaves two equal hemispheres.
Admit Card Date:17 April,2025 - 17 May,2025
Exam Date:01 May,2025 - 08 May,2025

Register for ALLEN Scholarship Test & get up to 90% Scholarship

Get up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes

This ebook serves as a valuable study guide for NEET 2025 exam.

This e-book offers NEET PYQ and serves as an indispensable NEET study material.
As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
We endeavor to keep you informed and help you choose the right Career path. Sign in and access our resources on Exams, Study Material, Counseling, Colleges etc.