NCERT Solutions for Class 7 Maths Chapter 4 Expressions Using Letter Numbers
Have you ever thought about how numbers and letters combine to form an algebraic expression? In the Class 7 Maths NCERT Chapter 4 Expressions using letter-numbers, students will be able to express the relationship between letters and numbers and their pattern mathematically. Additionally, they will also deepen their existing knowledge of arithmetic expressions and further understand the concept of simplifying algebraic expressions. The primary purpose of these NCERT solutions for Class 7 Maths is to provide students with clear and articulate answers to textbook exercises in a step-by-step manner, enabling learners to understand the concepts thoroughly and answer similar questions independently. Many toppers rely on NCERT Solutions because they are aligned with the latest syllabus.
This Story also Contains
- NCERT Solutions for Class 7 Maths Chapter 4 Expressions Using Letter-Numbers: Download Free PDF
- NCERT Solutions for Class 7 Maths Chapter 4 Expressions using Letter-Numbers: Exercise
- Expressions Using Letter-Numbers Class 7 NCERT Solutions: Topics
- NCERT Solutions for Class 7 Maths Chapter 4 Expressions Using Letter-Numbers: Notes
- Class 7 Maths Chapter 4 Expressions Using Letter-Numbers Solutions: Extra Question
- Why are Class 7 Maths Chapter 4 Expressions Using Letter-Numbers Question Answers Important?
- NCERT Solutions for Class 7 Maths Chapter Wise
- NCERT Books and NCERT Syllabus

Algebraic expressions turn numbers and letters into powerful methods for solving problems. Experienced Careers360 teachers curate these NCERT solutions for class 7 to make learning easier for students. These solutions to the 4th chapter of Class 7 provide detailed and step-by-step explanations for students. With the help of these solutions, they can practice the problems, verify their answer and strengthen their weak areas that need improvement. For detailed solutions, complete syllabus notes, and a free PDF download, refer to this NCERT article.
NCERT Solutions for Class 7 Maths Chapter 4 Expressions Using Letter-Numbers: Download Free PDF
Careers360 brings you NCERT Class 7 Maths Chapter 4 Expressions using Letter-Numbers solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 7 Maths Chapter 4 Expressions using Letter-Numbers: Exercise
Here are the NCERT Class 7 Maths Chapter 4 Expressions using Letter-Numbers question answers with clear and detailed solutions.
|
Expressions using Letter-Numbers Class 7 Question Answers Page number: 84-85 Number of Questions: 7 |
Question 1: Write formulas for the perimeter of:
(a) triangle with all sides equal.
(b) a regular pentagon (as we have learnt last year, we use the word ‘regular’ to say that all side lengths and angle measures are equal)
(c) a regular hexagon
Solution:
(a)
Formula of a triangle with three equal sides
= 3 × Side length
(b)
Formula of a regular Pentagon with five equal sides
= 5 × Side length
(c)
Formula of a regular Hexagon with six equal sides
= 6 × Side length
Question 2: Munirathna has a 20 m long pipe. However, he wants a longer watering pipe for his garden. He joins another pipe of some length to this one. Give the expression for the combined length of the pipe. Use the letter-number ‘k’ to denote the length in meters of the other pipe.
Solution:
Munirathna has a 20 m long pipe.
He joins another pipe of length k to this pipe.
So, total length of the pipe = (20 + k) m
Hence, the correct answer is (20 + k) m.
Question 3: What is the total amount Krithika has, if she has the following numbers of notes of ₹100, ₹20 and ₹5? Complete the following table:
|
|
|
|
|
|
|
|
| |
|
| |||
|
|
|
| |
|
|
|
|
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 4: Venkatalakshmi owns a flour mill. It takes 10 seconds for the roller mill to start running. Once it is running, each kg of grain takes 8 seconds to grind into powder. Which of the expressions below describes the time taken to complete grind ‘y’ kg of grain, assuming the machine is off initially?
(a) 10 + 8 + y
(b) (10 + 8) × y
(c) 10 × 8 × y
(d) 10 + 8 × y
(e) 10 × y + 8
Solution:
It takes 10 seconds for the roller mill to start running.
Each kg of grain takes 8 seconds to grind into powder.
So, y kg of grain will take = 8y seconds to grind into powder.
∴ Total time taken
= Time to start the machine + Time to grind y kg of grain
= (10 + 8y) seconds
Hence, the correct answer is option (d).
Question 5: Write algebraic expressions using letters of your choice.
(a) 5 more than a number
(b) 4 less than a number
(c) 2 less than 13 times a number
(d) 13 less than 2 times a number
Solution:
Let the initial number be k.
|
|
|
|
|
|
|
|
Question 6: Describe situations corresponding to the following algebraic expressions:
(a) 8 × x + 3 × y
(b) 15 × j – 2 × k
Solution:
(a)
The sum of 8 times x and 3 times y.
(b)
Subtraction 2 times k from 15 times j.
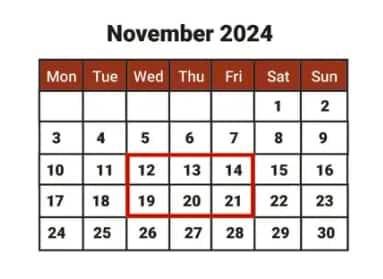
Question 7: In a calendar month, if any 2 × 3 grid full of dates is chosen as shown in the picture, write expressions for the dates in the blank cells if the bottom middle cell has the date ‘w’.
|
|
|
Solution:
As w = 20
So, 19 = w - 1
21 = w + 1
12 = w - 8
13 = w - 7
and 14 = w - 6
So, the complete table is as follows.
|
|
|
|
|
|
|
|
|
Expressions using Letter-Numbers Class 7 Question Answers Page number: 93-94 Number of Questions: 2 |
Question 1: Add the numbers in each picture below. Write their corresponding expressions and simplify them. Try adding the numbers in each picture in a couple of different ways and see that you get the same thing.
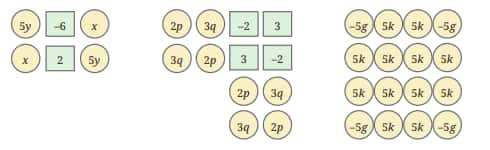
Solution:
We will check it in two ways.
Adding randomly:
(i)
$5y+(−6)+x+x+2+5y$
$=10y+2x−4$
(ii)
$2p+3q+(−2)+3+3q+2p+3+(−2)+2p+3q+3q+2p$
$=8p+12q+2$
(iii)
$-5g + 5k + 5k + (-5g) + 5k + 5k + 5k +$
$ 5k + 5k + 5k + 5k + 5k + (-5g) + 5k + 5k + (-5g)$
$= 60k - 20g$
Adding like terms together:
(i)
$(5y+5y)+(x+x)+(2−6)$
$=10y+2x+(−4)$
$=2x+10y−4$
(ii)
$(2p×4)+(3q×4)+(2×−2)+(3×2)$
$=8p+12q+(−4)+6$
$=8p+12q+2$
(iii)
$(5k×12)+(−5 g×4)$
$=60k+(−20 g)$
$=60k−20 g$
As we can see, the result will be the same no matter how we add the numbers from the pictures.
Question 2: Simplify each of the following expressions:
(a) p + p + p + p, p + p + p + q, p + q + p – q,
(b) p – q + p – q, p + q – p + q,
(c) p + q – (p + q), p – q – p – q
(d) 2d – d – d – d, 2d – d – d – c,
(e) 2d – d – (d – c), 2d – (d – d) – c,
(f) 2d – d – c – c
Solution:
(a)
p + p + p + p = 3p
p + p + p + q = 3p + q
p + q + p – q = 2q
(b)
p − q + p – q = 2p -2q
p + q – p + q = 2q
(c)
p + q − (p + q) = p + q – p – q = 0.
p – q – p – q = -2q
(d)
2d – d – d – d = 2d – 3d = -d
2d – d – d – c = 2d – 2d – c = -c
(e)
2d – d − (d – c) = 2d – d – d + c = 2d – 2d + c = c
2d − (d − d) – c = 2d – 0 – c = 2d – c
(f) 2d – d – c – c = d – 2c
|
Expressions using Letter-Numbers Class 7 Question Answers Page number: 102-105 Number of Questions: 15 |
For the problems asking you to find suitable expression(s), first try to understand the relationship between the different quantities in the situation described. If required, assume some values for the unknowns and try to find the relationship.
Question 1: One plate of Jowar roti costs ₹30, and one plate of Pulao costs ₹20. If x plates of Jowar roti and y plates of pulao were ordered in a day, which expression(s) describe the total amount in rupees earned that day?
(a) 30x + 20y
(b) (30 + 20) × (x + y)
(c) 20x + 30y
(d) (30 + 20) × x + y
(e) 30x – 20y
Solution:
If one plate of Jowar roti costs ₹30,
Then x plates of Jowar roti cost 30x.
If one plate of Pulao costs ₹20,
Then y plates of pulao cost 20y.
Total = 30x + 20y
Hence, the correct answer is option (a).
Question 2: Pushpita sells two types of flowers on Independence Day: champak and marigold. ‘p’ customers only bought champak, ‘q’ customers only bought marigold, and ‘r’ customers bought both. On the same day, she gave away a tiny national flag to every customer. How many flags did she give away that day?
(a) p + q + r
(b) p + q + 2r
(c) 2 × (p + q + r)
(d) p + q + r + 2
(e) p + q + r + 1
(f) 2 × (p + q)
Solution:
Let the set of customers who bought only Champak = p
Let the set of customers who bought only marigolds = q
Let the set of customers who bought both champak and marigold = r
∴ Total customers = p + q + r
Hence, the correct answer is option (a).
Question 3: A snail is trying to climb along the wall of a deep well. During the day it climbs up ‘u’ cm and during the night it slowly slips down ‘d’ cm. This happens for 10 days and 10 nights.
(a) Write an expression describing how far away the snail is from its starting position.
(b) What can we say about the snail’s movement if d > u?
Solution:
(a)
Daytime movement: The snail climbs up u cm during the day.
Nighttime movement: The snail slips down d cm during the night.
Net movement in a day = (u - v)
Net movement in 10 days = 10(u - v)
Hence, after 10 days and nights, the snail is 10(u - v) cm away from its starting position.
(b)
If d > u, it means the snail is slipping down more than it climbs up during each 24-hour cycle.
That also means, every day and night, the net distance snail will climb will be 0.
Hence, the snail will never escape the well, as it is effectively moving downward each day.
Question 4: Radha is preparing for a cycling race and practices daily. The first week, she cycles 5 km every day. Every week, she increases the daily distance cycled by ‘z’ km. How many kilometres would Radha have cycled after 3 weeks?
Solution:
In the first week, Radha cycles 5 km every day.
Total distance covered after that week = 7 × 5 = 35
Next week, Radha cycles (5 + z) km every day.
Total distance covered after that week = 7(5 + z)
Next week, Radha cycles (5 + z + z) km every day.
Total distance covered after that week = 7(5 + 2z)
∴ Total distance covered in 3 weeks by Radha
= 35 + 7(5 + z) + 7(5 + 2z)
= 35 + 35 + 7z + 35 + 14z
= 105 + 21z
Hence, the correct answer is (105 + 21z) km.
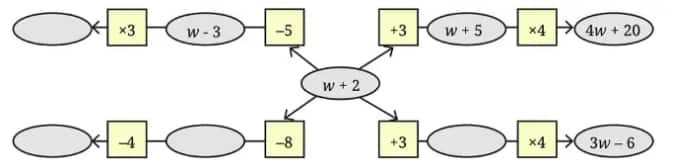
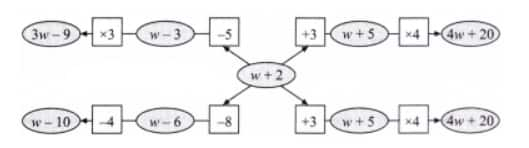
Question 5: In the following figure, observe how the expression w + 2 becomes 4w + 20 along one path. Fill in the missing blanks on the remaining paths. The ovals contain expressions, and the boxes contain operations.
Solution:
Question 6: A local train from Yahapur to Vahapur stops at three stations at equal distances along the way. The time taken in minutes to travel from one station to the next station is the same and is denoted by t. The train stops for 2 minutes at each of the three stations.
(a) If t = 4, what is the time taken to travel from Yahapur to Vahapur?
(b) What is the algebraic expression for the time taken to travel from Yahapur to Vahapur?
[Hint: Draw a rough diagram to visualise the situation]
Solution:
(a)
A local train from Yahapur to Vahapur stops at three stations at equal distances.
So, the train stops 3 times for 2 minutes each.
Total stoppage time = 3 × 2 = 6 minutes
The time taken in minutes to travel from one station to the next station is the same and is denoted by t.
Here t = 4
So, total time in travelling = 4 × 4 = 16 minutes
Hence, the total time taken to travel from Yahapur to Vahapur = 6 + 16 = 22 minutes
(b)

The time taken in minutes to travel from one station to the next station is the same and is denoted by t.
Total time in travelling = 4t
The train stops 3 times for 2 minutes each.
Total stoppage time = 3 × 2 = 6 minutes
Hence, the total time taken to travel from Yahapur to Vahapur = (4t + 6) minutes.
Question 7: Simplify the following expressions:
(a) 3a + 9b – 6 + 8a – 4b – 7a + 16
(b) 3 (3a – 3b) – 8a – 4b – 16
(c) 2 (2x – 3) + 8x + 12
(d) 8x – (2x – 3) + 12
(e) 8h – (5 + 7h) + 9
(f) 23 + 4(6m – 3n) – 8n – 3m – 18
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 8. Add the expressions given below:
(a) 4d – 7c + 9 and 8c – 11 + 9d
(b) – 6f + 19 – 8s and – 23 + 13f + 12s
(c) 8d – 14c + 9 and 16c – (11 + 9d)
(d) 6f – 20 + 8s and 23 – 13f – 12s
(e) 13m – 12n and 12n – 13m
(f) – 26m + 24n and 26m – 24n
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 9: Subtract the expressions given below:
(a) 9a – 6b + 14 from 6a + 9b – 18
(b) – 15x + 13 – 9y from 7y – 10 + 3x
(c) 17g + 9 – 7h from 11 – 10g + 3h
(d) 9a – 6b + 14 from 6a – (9b + 18)
(e) 10x + 2 + 10y from –3y +8 – 3x
(f) 8g + 4h – 10 from 7h – 8g + 20
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 10: Describe situations corresponding to the following algebraic expressions:
(a) 8x + 3y
(b) 15x – 2x
Solution:
|
|
|
|
|
|
|
|
|
Question 11: Imagine a straight rope. If it is cut once as shown in the picture, we get 2 pieces. If the rope is folded once and then cut as shown, we get 3 pieces. Observe the pattern and find the number of pieces if the rope is folded 10 times and cut. What is the expression for the number of pieces when the rope is folded r times and cut?

Solution:
When the rope is not folded and cut once → we get 2 pieces.
When the rope is folded once and cut → we get 3 pieces.
When the rope is folded twice and cut → we get 4 pieces.
When the rope is folded 3 times and cut → we get 5 pieces.
So, the pattern is:
Number of pieces = Number of folds + 2
So, if the rope is folded 10 times and cut, we get 10 + 2 = 12 pieces
When the rope is folded r times and cut, we get (r + 2) pieces.
Question 12: Look at the matchstick pattern below. Observe and identify the pattern. How many matchsticks are required to make 10 such squares? How many are required to make w squares?

Solution:
For one square, it needs 4 matchsticks.
For 2 squares, it needs 7 matchsticks.
For 3 squares, it needs 10 matchsticks.
So, the pattern is:
Total match sticks = Number of squares × 3 + 1
So, for 10 squares, we need (10 × 3 + 1) = 31 matchsticks
For w squares, we need [(w × 3) + 1] = (3w + 1) matchsticks
Question 13: Have you noticed how the colours change in a traffic signal? The sequence of colour changes is shown below. Find the colour at positions 90, 190, and 343. Write expressions to describe the positions for each colour.

Solution:
Red positions: 1, 5, 9, 13,
Yellow positions: 2, 4, 6, 8, 10, …..
Green positions: 3, 7, 11, 15.......
Let's first check the patterns.
For red lights:
Each term increases by 4.
So, the formula for the nth red position = (4n - 3), where n = 1, 2, 3, …..
For yellow lights:
These are all even numbers.
So, the formula for the nth yellow position = 2n, where n = 1, 2, 3, …..
For Green lights:
Each term increases by 4.
So, the formula for the nth green position = (4n - 1), where n = 1, 2, 3, …..
As we can see, all the even-numbered positions will show a yellow traffic signal light.
90 and 190 are even numbers. So, they will show yellow lights.
343 = 4 × 86 - 1, which is the pattern for Green lights.
Question 14: Observe the pattern below. How many squares will be there in Step 4, Step 10, and Step 50? Write a general formula. How would the formula change if we want to count the number of vertices of all the squares?

Solution:
Step 1: 5 squares
Step 2: 9 squares
Step 3: 13 squares
So, the pattern for the number of squares in the nth step is: 4n + 1, where n = 1, 2, 3, ….
In step 4: 4 × 4 + 1 = 17 squares
In step 10: 4 × 10 + 1 = 41 squares
In step 50: 4 × 50 + 1 = 201 squares
We know that a square has 4 vertices.
For (4n - 1) squares, the total vertices will be 4(4n + 1).
So, to count the vertices, the pattern will be 4(4n + 1), where n = 1, 2, 3, .....
Question 15: Numbers are written in a particular sequence in this endless 4-column grid.
(a) Give expressions to generate all the numbers in a given column (1, 2, 3, 4).
(b) In which row and column will the following numbers appear:
(i) 124 (ii) 147 (iii) 201
(c) What number appears in row r and column c?
(d) Observe the positions of multiples of 3.
Do you see any pattern in it? List other patterns that you see.
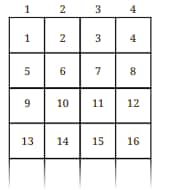
Solution:
(a)
Let r be the row number.
Column 1: 1, 5, 9, 13,…… which starts at 1 and adds 4 each row.
So, number in the rth row of column 1 = 4 × (r – 1) + 1
Column 2: 4 × (r – 1) + 2
Column 3: 4 × (r – 1) + 3
Column 4: 4 × (r – 1) + 4
If c is the column number, then the general formula to generate all numbers is 4 × (r – 1) + c.
(b)
(i) We divide each number by 4 to find its row and column
124 ÷ 4 ⇒ Quotient = 31 and remainder is 0
∴ 124 = 4 × 31 + 0 or 4 × 30 + 4
Comparing it with 4 × (r – 1) + c, we get,
r – 1 = 30, c = 4
So, r = 31 and c = 4
So, the row is 31 and the column is 4
(ii) 147 ÷ 4 ⇒ Quotient = 36 and remainder is 3
∴ 147 = 4 × 36 + 3
Comparing it with 4 × (r – 1) + c, we get,
r – 1 = 36, c = 3
So, 147 will appear at row 36 + 1 = 37 and column 3
(iii) 201 ÷ 4 ⇒ Quotient = 50 and remainder is 1
∴ 201 = 4 × 50 + 1
Comparing it with 4 × (r – 1) + c, we get,
r – 1 = 50, c = 1
So, 201 will appear at row 51 and column 1.
(c)
The number that appears in row r and column c is 4(r – 1) + c.
(d)
Every third number is a multiple of 3.
We can observe that even numbers always appear in column 2 and column 4.
Odd numbers always appear in column 1 and column 3.
Every row has 2 odd and 2 even numbers.
The sum of each row increases by 16.
Expressions Using Letter-Numbers Class 7 NCERT Solutions: Topics
Students will explore the following topics in NCERT Class 7 Maths Chapter 4 Expressions Using Letter-Numbers:
- The Notion of Letter-Numbers
- Revisiting Arithmetic Expressions
- Omission of the Multiplication Symbol in Algebraic Expressions
- Simplification of Algebraic Expressions
- Pick Patterns and Reveal Relationships
NCERT Solutions for Class 7 Maths Chapter 4 Expressions Using Letter-Numbers: Notes
Careers360 has prepared these Class 7 Expressions Using Letter-Numbers Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Class 7 Maths Expressions Using Letter-Numbers question answers and solve them independently from next time.
Arithmetic Expressions
Addition: Addition is the process of combining two or more numbers to find their total or sum.
Example: You have 7 apples, and your friend gives you 3 more apples.
Now you have 7 + 3 = 10 apples
Subtraction: Subtraction is the process of taking away one number from another to find the difference between them.
Example: You have 9 chocolates. You eat 4 chocolates.
Now you have 9 – 4 = 5 chocolates left.
Multiplication: Multiplication is the process of adding a number to itself a certain number of times. It is the repeated addition of the same number.
Example: You have 3 baskets. Each basket has 6 mangoes.
So total mangoes = 6 + 6 + 6 = 18
Or simply, 6 × 3 = 18
Division: Division is the process of splitting a number into equal parts or groups. It shows how many times one number is contained in another.
Example: You have 12 biscuits and you want to share them equally among 3 friends.
Each friend will get 12 ÷ 3 = 4 biscuits.
Omission of the Multiplication Symbol in Algebraic Expressions
In algebra, the multiplication sign is usually omitted to avoid confusion with the variable x. Instead of writing the multiplication symbol, we write terms side by side.
Example: Instead of writing 4 × x, we write 4x
Instead of writing a × b, we write ab
Instead of writing 3 × a × b, we write 3ab
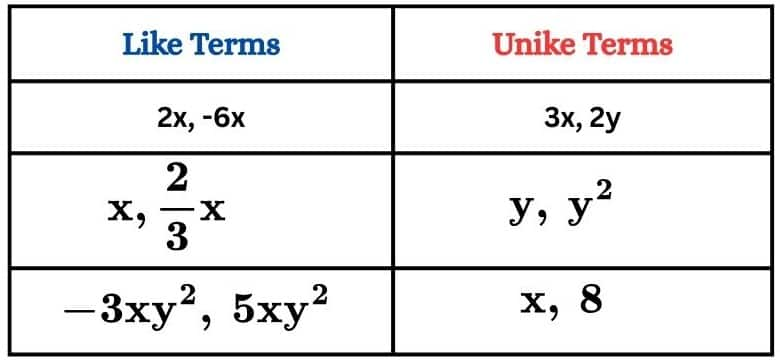
Like terms and Unlike terms
Like terms have the same variables to the same power. Like terms can be combined.
Unlike terms are the exact opposite. They have different variables and different powers. They can't be combined.
Simplification of Algebraic Expressions
Simplification of algebraic expressions means reducing a given expression to its simplest form by combining like terms and performing operations such as addition, subtraction, multiplication, or division.
Here are the steps of simplification.
1. Remove brackets using distributive law, if any.
Example: $3(x+4)=3 x+12$
2. Combine like terms (terms that have the same variables with the same powers).
Example: $5 x+7 x=12 x$
3. Arrange terms neatly, usually in standard form (highest power first).
Example: $2+7 x+x^2=x^2+7 x+2$
4. Simplify constants and perform arithmetic operations.
Example: $12-5+x=7+x$
Class 7 Maths Chapter 4 Expressions Using Letter-Numbers Solutions: Extra Question
Question:
Simplify the expression:
$3 x+7+5 x-4+2$
Solution:
To simplify, we know we have to first group the like terms.
Here, like terms are $3x,5x$ and $7,-4,2$
So,
$3 x+7+5 x-4+2$
$=8x+5$
Hence, the correct answer is $(8x+5)$.
Why are Class 7 Maths Chapter 4 Expressions Using Letter-Numbers Question Answers Important?
The chapter Expressions Using Letter-Numbers will introduce students in class 7 to an essential branch of mathematics, algebra. The chapter also includes important concepts, such as simplifying algebraic expressions and omitting the multiplication symbols in algebraic expressions. Here’s why the Class 7 Maths Expressions Using Letter-Numbers question answers are important.
- Practising questions from this chapter will help students in future during the reasoning questions, as they will be already familiar with the concept of expressing numbers using letters.
- Expressions are used to represent everyday situations mathematically, like cost, area, or speed. Solving questions helps students relate maths to real-world problems.
- Questions from this chapter often appear in school exams and Olympiads. So, checking these solutions will help students to improve their confidence and scoring ability.
NCERT Solutions for Class 7 Maths Chapter Wise
We at Careers360 compiled all the NCERT class 7 Maths solutions in one place for easy student reference. The following links will allow you to access them.
NCERT Books and NCERT Syllabus
Students can also check the Class 7 NCERT Books and the NCERT Syllabus here:
Frequently Asked Questions (FAQs)
The topics discussed in the NCERT Class 7 Maths Chapter 4 Expressions using Letter-Numbers are:
- The Notion of Letter-Numbers
- Revisiting Arithmetic Expressions
- Omission of the Multiplication Symbol in Algebraic Expressions
- Simplification of Algebraic Expressions
- Pick Patterns and Reveal Relationships
Class 7 Maths Chapter 4 Solutions provide step-by-step solutions, clear examples for simplifying expressions, combining like terms, and applying the formulas in practical scenarios.
A letter-number is a symbol (like x or y) that represents an unknown number or changing quantity, helping to write general rules and formulas.
Like terms have the same variable part (e.g. 5c and 10c). To combine, just add or subtract their coefficients:
5c + 10c = 15c
Convert statements like "5 more than a number x" into x + 5, or "cost of 7 items at Rs. c" into 7c. Class 7 Maths Chapter 4 Solutions provides many such examples.
Students can download Expressions Using Letter-Numbers Class 7 Solutions PDF from trusted educational sources such as Careers360. Students can find the free downloadable PDF in this article itself.
A coefficient is the number multiplied by a variable.
Example: In 7x, the coefficient is 7.
A variable is a symbol, usually a letter like x, y, or n, that stands for a number whose value can change.
Example: In 2x + 3, x is the variable.
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
