NCERT Solutions for Class 7 Maths Chapter 1 Large Number Around Us
From population data to astronomical distances, we are surrounded by large numbers. NCERT Class 7 Chapter 1 Large Numbers Around Us introduces us to this exciting world of large numbers. In this chapter, we will learn how to read, write, and compare large numbers in both the Indian and international systems. Understanding large numbers will build a strong foundation for the students and enhance their problem-solving abilities. This article includes NCERT textbook exercise solutions, proper notes on the chapter, key topics, and points to remember, which will help students grasp the core concepts of the chapter with clarity and confidence. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus.
This Story also Contains
- NCERT Solutions for Class 7 Maths Chapter 1 Large Numbers Around Us: Download Free PDF
- NCERT Solutions for Class 7 Maths Chapter 1 Large Numbers Around Us Solutions: Exercise
- NCERT Large Numbers Around Us Class 7 Chapter 1 Maths: Topics
- Class 7 Maths Chapter 1 Large Numbers Around Us Solutions: Extra Question
- NCERT Solutions for Class 7 Maths Chapter 1 Large Numbers Around Us: Notes
- NCERT Solutions for Class 7 Maths Chapter 1 - Points to Remember
- Why are Class 7 Maths Chapter 1 Large Numbers Around Us Question Answers Important?
- NCERT Solutions for Class 7 Maths Chapter-wise
- NCERT Books and Syllabus

This article contains comprehensive solutions for all the questions in this chapter. These NCERT Solutions for Class 7 Maths offer detailed and step-by-step explanations to support students. With the help of these solutions, they can practice the problems, verify their answer and strengthen their weak areas that need improvement. This will also clear their doubts and provide them with a proper understanding of the chapter's concepts. These NCERT Solutions for Class 7 are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 7 Maths Chapter 1 Large Numbers Around Us: Download Free PDF
Careers360 brings you NCERT Class 7 Maths Chapter 1 Large Numbers Around Us question answers, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 7 Maths Chapter 1 Large Numbers Around Us Solutions: Exercise
Below are the detailed Class 7 Maths Chapter 1 Large Numbers Around Us question answers provided in the textbook.
|
Large Numbers Around Us Class 7 Question Answers |
Figure it Out
Q1: According to the 2011 Census, the population of the town of Chintamani was about 75,000. How much less than one lakh is 75,000?
Answer:
One lakh = 1,00,000
Now, 1,00,000 – 75,000 = 25,000
So, 75,000 is 25,000 less than one lakh.
Q2: The estimated population of Chintamani in the year 2024 is 1,06,000. How much more than one lakh is 1,06,000?
Answer:
One lakh = 1,00,000
Now, 1,06,000 – 1,00,000 = 6,000.
So, 1,06,000 is 6,000 more than one lakh.
Q3: By how much did the population of Chintamani increase from 2011 to 2024?
Answer:
To find the increase, we subtract the 2011 population from the 2024 estimated population.
– Calculation: 1,06,000 (2024 pop) – 75,000 (2011 pop) = 31,000.
The population increased by 31,000 from 2011 to 2024.
|
Large Numbers Around Us Class 7 Question Answers Page Number: 6 Question: 1 |
Figure it Out
For each number given below, write expressions for at least two different ways to obtain the number through button clicks. Think like Chitti and be creative.
(a) 8300 (b) 40629 (c) 56354 (d) 66666 (e) 367813
Answer:
(a) 8300
First way: (8 × 1000) + (3 × 100) = 8300
Second way: (5 × 1000) + (30 × 100) + (30 × 10) = 8300
(b) 40629
First way: (4 × 10,000) + (6 × 1,00) + (2 × 10) + (9 × 1) = 40,000 + 600 + 20 + 9 = 40,629.
Second way: (406 × 100) + (29 × 1) = 40,600 + 29 = 40,629.
(c) 56354
First way: (5 × 10,000) + (6 × 1,000) + (3 × 100) + (5 × 10) + (4 × 1) = 50,000 + 6,000 + 300 + 50 + 4 = 56,354
Second way: (563 × 100) + (5 × 10) + (4 × 1) = 56,300 + 50 + 4 = 56,354
(d) 66666
First way: (6 × 10000) + (6 × 1000) + (6 × 100) + (6 × 10) + (6 × 1) = 66666
Second way: (66 × 1000) + (6 × 100) + (6 × 10) + (6 × 1) = 66666
(e) 367813
First way: (3 × 100000) + (6 × 10000) + (7 × 1000) + (8 × 100) + (1 × 10) + (3 × 1) = 367813
Second way: (30 × 10000) + (60 × 1000) + (70 × 100) + (81 × 10) + (3 × 1) = 367813
|
Large Numbers Around Us Class 7 Question Answers Page Number: 7 Questions: 3 |
Figure it Out
Q1: For the numbers in the previous exercise, find out how to get each number by making the smallest number of button clicks and write the expression.
Answer:
(a) 8300
(8 × 1,000) + (3 × 100) = 8300
8300 can be obtained in (8 + 3) = 11 clicks.
(b) 40629
(4 × 10,000) + (6 × 100) + (2 × 10) + (9 × 1) = 40629
40629 can be obtained in (4 + 6 + 2 + 9) = 21 clicks.
(c) 56354
(5 × 10,000) + (6 × 1,000) + (3 × 100) + (5 × 10) + (4 × 1) = 56354
56354 can be obtained in (5 + 6 + 3 + 5 + 4) = 23 clicks.
(d) 66666
(6 × 10,000) + (6 × 1,000) + (6 × 100) + (6 × 10) + (6 × 1) = 66666
66666 can be obtained in (6 + 6 + 6 + 6 + 6) = 30 clicks.
(e) 367813
(3 × 1,00,000) + (6 × 10,000) + (7 × 1,000) + (8 × 100) + (1 × 10) + (3 × 1) = 367813
367813 can be obtained in (3 + 6 + 7 + 8 + 1 + 3) = 28 clicks.
Q2: Do you see any connection between each number and the corresponding smallest number of button clicks?
Answer:
The smallest number of button clicks equals the sum of the digits in the number's place value form, using the largest possible button for each digit.
Therefore, the smallest number of button clicks for each number is the sum of its digits.
Q3: If you notice, the expressions for the least button clicks also give the Indian place value notation of the numbers. Think about why this is so.
Answer:
The Indian place value system helps in identifying and differentiating between numbers easily by grouping them into thousands, lakhs, crores, etc.
|
Large Numbers Around Us Class 7 Question Answers Page Number: 9 Questions: 3 |
Figure it Out
Q1: Read the following numbers in Indian place value notation and write their number names in both the Indian and American systems: (a) 4050678, (b) 48121620, (c) 20022002, (d) 246813579, (e) 345000543, (f) 1020304050.
Answer:
(a) 4050678
Indian: 40,50,678 = Forty lakh fifty thousand six hundred seventy-eight.
American: 4,050,678 = Four million fifty thousand six hundred seventy-eight.
(b) 48121620
Indian: 4,81,21,620 = Four crore eighty-one lakh twenty-one thousand six hundred twenty.
American: 48,121,620 = Forty-eight million one hundred twenty-one thousand six hundred twenty.
(c) 20022002
Indian: 2,00,22,002 = Two crore twenty-two thousand two.
American: 20,022,002 = Twenty million twenty-two thousand two.
(d) 246813579
Indian: 24,68,13,579 = Twenty-four crore sixty-eight lakh thirteen thousand five hundred seventy-nine.
American: 246,813,579 = Two hundred forty-six million eight hundred thirteen thousand five hundred seventy-nine.
(e) 345000543
Indian: 34,50,00,543 = Thirty-four crore fifty lakh five hundred forty-three.
American: 345,000,543 = Three hundred forty-five million five hundred forty-three.
(f) 1020304050
Indian: 1,02,03,04,050 = One Arab two crore three lakh four thousand fifty.
American: 1,020,304,050 = One billion, two million three hundred four thousand fifty.
Q2: Write the following numbers in Indian place value notation: (a) One crore one lakh one thousand ten, (b) One billion one million one thousand one, (c) Ten crore twenty lakh thirty thousand forty, (d) Nine billion eighty million seven hundred thousand six hundred.
Answer:
(a) One crore one lakh one thousand ten
⇒ 1,01,01,010
(b) One billion one million one thousand one
⇒ 1,001,001,001
(c) Ten crore twenty lakh thirty thousand forty
⇒ 10,20,30,040
(d) Nine billion eighty million seven hundred thousand six hundred
⇒ 9,080,700,600
Q3: Compare and write ‘<’, ‘>’ or ‘=’: (a) 30 thousand ____ 3 lakhs (b) 500 lakhs ______ 5 million (c) 800 thousand ____ 8 million (d) 640 crore ______ 60 billion.
Answer:
(a) 30,000 (< ) 3,00,000
⇒ 30 thousand (<) 3 lakhs.
(b) 5,00,00,000 (> ) 5,000,000
⇒ 500 lakhs (>) 5 million.
(c) 8,00,000 (< ) 5,000,000
⇒ 800 thousand (<) 8 million.
(d) 6,40,00,00,000 (< ) 60,000,000,000
⇒ 640 crore (< ) 60 billion.
|
Large Numbers Around Us Class 7 Question Answers Page Number: 14 Questions: 2 |
Figure it Out
Q1: Find quick ways to calculate these products:
(a) 2 × 1768 × 50,
(b) 72 × 125 [Hint: 125 = $\frac{1000}8$ ],
(c) 125 × 40 × 8 × 25
Answer:
(a) 2 × 1768 × 50
= 2 × 50 × 1768
= 100 × 1768
= 17680.
(b) 72 × 125
= 72 × $\frac{1000}8$
= 9 × 1000
= 9000
(c) 125 × 40 × 8 × 25
= 125 × 8 × 40 × 25
= 1000 × 1000
= 10,00,000.
Q2: Calculate these products quickly.
(a) 25 × 12 = _____________,
(b) 25 × 240 = _____________,
(c) 250 × 120 = _____________,
(d) 2500 × 12 =_____________,
(e) ______×______= 120000000
Answer:
(a) 25 × 12
= $\frac{100}4$ × 12
= 100 × 3
= 300.
(b) 25 × 240
= $\frac{100}4$ × 240
= 100 × 60
= 6000.
(c) 250 × 120
= $\frac{1000}4$ × 120
= 1000 × 30
= 30000.
(d) 2500 × 12
= $\frac{10000}4$ × 12
= 10,000 × 3
= 30,000.
(e) 1200 × 1,00,000 = 12,00,00,000.
|
Large Numbers Around Us Class 7 Question Answers Page Number: 19 Questions: 14 |
Figure it Out
Q1: Using all digits from 0 – 9 exactly once (the first digit cannot be 0) to create a 10-digit number, write the —
(a) Largest multiple of 5 (b) Smallest even number
Answer:
(a) Largest multiple of 5 = 9876543210 (ends in 0, divisible by 5).
(b) Smallest even number = 1023456798 (ends in 2, even).
Q2: The number 10,30,285 in words is Ten lakhs thirty thousand two hundred eighty five, which has 43 letters. Give a 7-digit number name which has the maximum number of letters.
Answer:
77,77,777 (Seventy-seven lakhs seventy-seven thousand seven hundred seventy-seven).
This has 61 letters, making it one of the longest 7-digit numbers.
Q3: Write a 9-digit number where exchanging any two digits results in a bigger number. How many such numbers exist?
Answer:
A 9-digit number where exchanging any two digits results in a bigger number = 987654321. Only one such number exists.
Q4: Strike out 10 digits from the number 12345123451234512345 so that the remaining number is as large as possible.
Answer:
Striking out smaller numbers 1,2,3,4 from the given number, we get 5534512345.
Q5: The words ‘zero’ and ‘one’ share letters ‘e’ and ‘o’. The words ‘one’ and ‘two’ share a letter ‘o’, and the words ‘two’ and ‘three’ also share a letter ‘t’. How far do you have to count to find two consecutive numbers which do not share an English letter in common?
Answer:
Let’s check:
one & two share o
two & three share t, e
three & four share r
four & five share f
five & six share i
Six & seven share s
seven & eight share e
eight & nine share e, i, n
nine & ten share n, e
It shows that all consecutive numbers have at least one common letter.
So, there is no such pair of consecutive numbers that do not share an English letter in common.
Q6: Suppose you write down all the numbers 1, 2, 3, 4, …, 9, 10, 11, ... The tenth digit you write is ‘1’ and the eleventh digit is ‘0’, as part of the number 10. (a) What would the 1000th digit be? At which number would it occur? (b) What number would contain the millionth digit? (c) When would you have written the digit ‘5’ for the 5000th time?
Answer:
(a) Digits from 1 to 9 = 9 digits
Digits from 10 to 99 = 90 numbers × 2 = 180 digits
Total digits from 1 to 99 = 189 digits
Remaining digits to reach 1000th digit = 1000 – 189 = 811
Numbers with 3 3-digit numbers = 811/3 = 270 full numbers + 1 digit left over.
The first 3-digit number is 100
270th 3 digit number is 100 + 270 – 1 = 369
The next number is 370.
The first digit of 370, which is 3, is the 1000th digit.
(b) Let's calculate:
1-9: 9 × 1=9 digits
10-99: 90 × 2 = 180 digits
100-999: 900 × 3 = 2700 digits
1000-9999: 9000 × 4 = 36,000 digits
10000-99999: 90,000 × 5 = 450,000 digits
100000-999999: 900,000 × 6 = 5,400,000 digits
So, the millionth digit must lie within the 100000-999999 range (6-digit numbers).
Let's subtract the earlier ranges first:
Total digits before 6-digit numbers:
9 + 180 + 2700 + 36000 + 450000 = 488,889 digits
Digits remaining to reach 1,000,000:
1,000,000 - 488,889 = 511,111 digits
Each 6-digit number = 6 digits
511111/6 = 85,185, full numbers = 511,110 digits, with 1 digit left
Start of 6-digit numbers: 100000
85,185th number =100000 + 85184 = 185184
So, the millionth digit is the first digit of the number 185185.
(c) Single-digit numbers (1-9): 1 (only 5)
Two-digit numbers (10-99)
- (15, 25, 35,..., 95), totalling 9 occurrences.
- 50, 51, 52, ..., 59, totalling 10 occurrences.
Thus, 19 occurrences of the digit 5 in the range 10-99.
Total occurrences so far: $1+19=20$
Three-digit numbers (100-999)
(i) Units position: Numbers like 105, 115, ....., 995 contribute 10 occurrences per 100 numbers. Across 900 numbers, there are 90 occurrences.
(ii) Tens position: Numbers like 150-159, 250-259, ......, 950-959 also contribute 10 occurrences per 100 numbers, and 90 occurrences in all.
(iii) Hundreds position: Numbers like 500-599 contribute 100 occurrences in this range.
Thus, 90 (units) + 90 (tens) + 100 (hundreds) = 280 occurrences
Total occurrences so far: $20+280=300$
Four-digit numbers (1000-9999)
Now it gets more intense! Here, 5 appears in four positions (units, tens, hundreds, thousands):
(i) Units position: Every 10 numbers, e.g., 1005, 1015, ..., 9995 = 900 occurrences total.
(ii) Tens position: 1050-1059, 1150-1159, ..., 9950-9959. That's 900 occurrences total.
(iii) Hundreds position: 1500-1599,2500-2599,..., 9500-9599 = 900 occurrences total.
(iv) Thousands position: 5000-5999 $=1000$ occurrences
Adding these up: 900 (units) +900 (tens) +900 (hundreds) +1000 (thousands) $=3700$ occurrences
Total occurrences so far: $300+3700=4000$
Numbers starting from 10000 onward
For the 5000th number, we require $5000-4000=1000$ more numbers that lie in 10001-10999.
(v) Among 10000-10999, one digit 5 appears in 100 numbers (e.g., 10005, 10015,....., 10995).
The digit 5 appears in 100 numbers (e.g., 10050-10059, ..., 10950-10959).
The digit 5 appears in 100 numbers (e.g., 10500-10599).
Total 4000 + 300 = 4300
In 11000-11999
5 at unit place = 100
5 at tens place = 100
5 at a hundred place = 100
Total 4300 + 300 = 4600
In 12000-12999
4600 + 300 = 4900
In 13000-13999
Unit = 100
Total = 5000
Final number = 13995
Q7: A calculator has only ‘+10,000’ and ‘+100’ buttons. Write an expression describing the number of button clicks to be made for the following numbers: (a) 20,800, (b) 92,100, (c) 1,20,500, (d) 65,30,000, (e) 70,25,700.
Answer:
(a) 20,800
$(2 \times 10,000)+(8 \times 100)=20,000+800=20,800(10$ clicks $)$.
(b) 92,100
$(9 \times 10,000)+(21 \times 100)=90,000+2,100=92,100(30$ clicks $)$.
(c) $1,20,500$
$(12 \times 10,000)+(5 \times 100)=1,20,000+500=1,20,500$ ( 17 clicks).
(d) $65,30,000$
$(653 \times 10,000)=65,30,000(653$ clicks $)$.
(e) 70,25,700
$(702 \times 10,000)+(57 \times 100)=70,20,000+5,700=70,25,700$ ( 759 clicks).
Q8: How many lakhs make a billion?
Answer:
1 billion = 1000 million = 1000 × 10 lakhs = 10,000 lakhs.
Q9: You are given two sets of number cards numbered from 1 – 9. Place a number card in each box below to get the (a) largest possible sum, (b) smallest possible difference of the two resulting numbers.
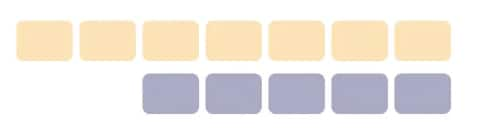
Answer:
(a)
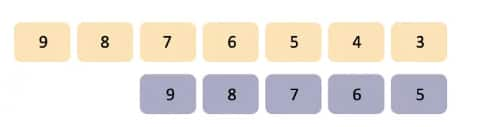
To get the largest possible sum, both the 7-digit and 5-digit numbers need to be the largest.
7-digit number = 98,76,543
5-digit number = 98,765
Sum = 98,76,543 + 98,765 = 99,75,308.
(b)
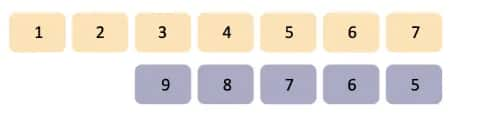
To get the smallest possible difference, the 7-digit number needs to be the smallest, and the 5-digit number needs to be the largest.
7-digit number = 12,34,567
5-digit number = 98,765
Difference = 12,34,567 – 98,765 = 11,35,802
Q10: You are given some number cards: 4000, 13000, 300, 70000, 150000, 20, and 5. Using the cards, get as close as you can to the numbers below using any operation you want. Each card can be used only once to make a particular number.
(a) 1,10,000: Closest I could make is 4000 × (20 + 5) + 13000 = 1,13,000
(b) 2,00,000:
(c) 5,80,000:
(d) 12,45,000:
(e) 20,90,800:
Answer:
(a) 1,10,000:
Closest estimate = 70,000 + (4,000 × 5) + 13,000 = 1,03,000.
(b) 2,00,000:
Closest estimate = 1,50,000 + 70,000 – (4,000 × 5) = 2,00,000.
(c) 5,80,000:
Closest estimate = (1,50,000 × 4) – (4000 × 5) = 5,80,000.
(d) 12,45,000:
Closest estimate = (1,50,000 × 8) + (13,000 × 4) – 4,000 = 12,48,000.
(e) 20,90,800:
Closest estimate = (1,50,000 × 14) + 4000 – 13000 = 20,91,000.
Q11: Find out how many coins should be stacked to match the height of the Statue of Unity. Assume each coin is 1 mm thick.
Answer:
Statue of Unity = 180 metres = 180,000 mm.
Coins $=180,000 \div 1=1,80,000$ coins.
Q12: Grey-headed albatrosses have a roughly 7-foot wingspan. They are known to migrate across several oceans. Albatrosses can cover about 900 – 1000 km in a day. One of the longest single trips recorded is about 12,000 km. How many days would such a trip take to cross the Pacific Ocean, approximately?
Answer:
Total trip = 12,000 km
Distance covered in a day = 900 – 1000 km
Estimated Number of days if it flies 900 km/day = 12,000/900 = 13.3 days
Estimated Number of days if it flies 1000 km/day = 12,000/1,000 = 12 days
∴ It would take approximately 12 to 14 days for a grey-headed albatross to complete a 12,000 km trip across the Pacific Ocean.
Q13: A bar-tailed godwit holds the record for the longest recorded non-stop flight. It travelled 13,560 km from Alaska to Australia without stopping. Its journey started on 13 October 2022 and continued for about 11 days. Find out the approximate distance it covered every day. Find out the approximate distance it covered every hour.
Answer:
Total distance = 13,560 km
Duration = 11 days
Each day = 24 hours
Duration in hours = 11 × 24 = 264 hours
Distance covered per day = (13,560 km)/(11 days) = 1232.73 km or 1233 km.
Distance covered per hour = (13,560 km)/(264 hours) = 51.36 km or 51 km.
Q14: Bald eagles are known to fly as high as 4500 – 6000 m above the ground level. Mount Everest is about 8850 m high. Aeroplanes can fly as high as 10,000 – 12,800 m. How many times bigger are these heights compared to Somu’s building?
Answer:
Height of Somu’s building = 40 m
(i) Bald eagles’ flight height = 4500 – 6000 m
Lower estimate = $\frac{4500}{40}$ = 112.5
Upper estimate = $\frac{6000}{40}$ = 150
∴ Bald eagles fly about 112 to 150 times higher than Somu’s building.
(ii) Mount Everest height = 8850 m
$\frac{8850}{40}$ = 221.25
∴ Mount Everest is about 221 times taller than Somu’s building.
(iii) Aeroplanes flight height = 10,000 – 12,000 m
Lower estimate = (10,000 )/(40 ) = 250
Upper estimate = (12,000 )/(40 ) = 320
∴ Aeroplanes fly about 250 to 320 times higher than Somu’s building.
NCERT Large Numbers Around Us Class 7 Chapter 1 Maths: Topics
Topics you will learn in NCERT Class 7 Maths Chapter 1 Large Numbers Around Us include:
- A Lakh Varieties!
- Reading and Writing Numbers
- Land of Tens
- Of Crores and Crores!
- Exact and Approximate Values
- Patterns in Products
- Did You Ever Wonder…?
Class 7 Maths Chapter 1 Large Numbers Around Us Solutions: Extra Question
Question:
The population of four metro cities is given below:
-
Delhi: 1,67,87,941
-
Mumbai: 1,24,42,373
-
Kolkata: 1,47,87,779
-
Chennai: 1,08,66,444
(a) Arrange the populations in ascending order.
(b) Arrange the populations in descending order.
(c) Which city has the largest population, and which has the smallest?
Answer:
(a) Ascending order (smallest to largest):
Chennai (1,08,66,444) < Mumbai (1,24,42,373) < Kolkata (1,47,87,779) < Delhi (1,67,87,941)
(b) Descending order (largest to smallest):
Delhi (1,67,87,941) > Kolkata (1,47,87,779) > Mumbai (1,24,42,373) > Chennai (1,08,66,444)
(c) Largest population: Delhi (1,67,87,941)
Smallest population: Chennai (1,08,66,444)
NCERT Solutions for Class 7 Maths Chapter 1 Large Numbers Around Us: Notes
Careers360 has prepared these Class 7 Large Numbers Around Us Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Large Numbers Around Us NCERT solutions and solve them independently from next time.
Indian Number System
Digits are similar to → ones, tens, hundreds, thousands, lakhs, crores, etc.
Commas are inserted after 3 digits from the right (hundreds), then after each 2 digits.
Example:
5,26,75,384 → Five crore twenty-six lakh seventy-five thousand three hundred eighty-four.
International Number System
Digits are similar to → ones, tens, hundreds, thousands, lakhs, crores, etc.
Commas are inserted every 3 digits from the right.
Example:
123,456,789 → One hundred twenty-three million four hundred fifty-six thousand seven hundred eighty-nine
Comparison of Numbers
We can compare numbers digit by digit, from the left.
Keep in mind that a number with higher digits is always larger.
Example:
5,00,000 is greater than 50,000
9,98,000 is greater than 9,80,000
Estimation and Rounding Off
We can apply approximation or estimation of large numbers for simpler calculations.
Rounding Rules:
If the digit to the right is 5 or above, then we add 1 to the digit.
If the digit to the right is less than 5, then we leave the same digit unchanged.
Examples:
3,786 → nearest to 100 = 3,800
68,490 → nearest to 1,000 = 68,000
1,29,468 → nearest 10,000 = 1,30,000
Application of Large Numbers in Day-to-Day Life
Population: India has a population of about 1.4 billion.
Distance: The distance between the Earth and the Sun is approximately 149,600,000 km.
Money: Salaries, budgets of the government, and profits of businesses are usually in lakhs and crores.
Data: Scores in sports, views on social media, and storage in gigabytes, such as 1 GB = 1,000,000,000 bytes.
Important Terms
| Lakh | 1,00,000 (Indian) |
| Crore | 1,00,00,000 (Indian) |
| Million | 1,000,000 (International) |
| Billion | 1,000,000,000 (International) |
| Estimation | Approximating a number |
| Rounding Off | Simplifying a number based on place value |
| Place Value | The value of a digit depends on its position |
NCERT Solutions for Class 7 Maths Chapter 1 - Points to Remember
Check the following important points to understand and solve Class 7 Maths Chapter 1 Large Numbers Around Us question answers effectively.
- The Indian Number System has lakh (1,00,000) and crore (1,00,00,000).
- The International Number System has million (1,000,000) and billion (1,000,000,000).
- In the Indian system, commas occur after 3 digits, then after each 2 digits.
- In the International system, commas occur after every 3 digits from the right.
- When comparing large numbers, start verifying from the leftmost digit.
- A number with a higher number of digits is always larger than one with fewer digits.
- Estimation facilitates quick computation with big numbers.
- While rounding, if the following digit is 5 or higher, round up; otherwise, round down.
Why are Class 7 Maths Chapter 1 Large Numbers Around Us Question Answers Important?
The first chapter of class 7, Large Numbers Around Us, is an important part of the Number system. Many important concepts, such as how to write and evaluate large numbers, Exact and Approximate Values, and finding patterns in them, are discussed in these solutions. Here’s why the Class 7 Maths Large numbers around us question answers are important.
- Dealing with large numbers is essential for future chapters, such as integers, algebra, data handling, and practical arithmetic, in Classes 8 to 10.
- This chapter connects maths with real-world applications such as population data, distance between planets, money in the economy, and big calculations seen in newspapers and news reports.
- In this chapter, Exercises in Land of Tens and Reading and Writing Numbers help students work comfortably with very large numbers and avoid calculation mistakes.
- By practising these NCERT question answers, students score better in school exams and develop a strong base for future competitive exams like NTSE, Olympiads, and more.
NCERT Solutions for Class 7 Maths Chapter-wise
Access all NCERT Class 7 Maths solutions from one place using the links below.
NCERT Books and Syllabus
Students can also check the NCERT Books and the NCERT Syllabus here:
Frequently Asked Questions (FAQs)
The greatest 6-digit number is 999999, and the smallest 7-digit number is 1000000.
Large numbers appear in population data, distances between cities, national income, votes, sports scores, and scientific calculations.
These NCERT solutions, prepared by experts at Careers360, strengthen concept clarity, improve calculation accuracy, and help students handle word problems involving large numbers confidently.
Numbers are grouped in thousands and millions.
For example, 1,234,567 is read as one million two hundred thirty-four thousand five hundred sixty-seven.
Exact values give the precise number, while approximate values are rounded off for easier understanding.
Large numbers are used in real life, such as population data, distances in space, money transactions, and statistics.
Yes, many educational platforms, such as Careers360, offer free downloadable PDFs of NCERT Large Numbers Around Us Class 7 Solutions. Students can find the free downloadable PDF in this article itself.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
