• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 8.1 Class 10 Maths Chapter 8 - Introduction to Trigonometry

NCERT Solutions for Exercise 8.1 Class 10 Maths Chapter 8 - Introduction to Trigonometry

Edited By Ramraj Saini | Updated on Nov 27, 2023 08:44 AM IST | #CBSE Class 10th

NCERT Solutions For Class 10 Maths Chapter 8 Exercise 8.1

NCERT Solutions for Exercise 8.1 Class 10 Maths Chapter 8 Introduction to Trigonometry are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 maths ex 8.1 deal with the concept of trigonometry and trigonometric ratios. The Branch of Mathematics that deals with the measurement of sides and angles of a triangle is known as trigonometry. Trigonometric Ratios are nothing but the ratios of the sides of a right triangle with respect to its acute angles. Trigonometrically, there are six ratios.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 8 Exercise 8.1
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1
  3. Assess NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1
  4. More About NCERT Solutions for Class 10 Maths Exercise 8.1: Trigonometric Ratios
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 8.1:
  6. NCERT Solutions Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 8.1 Class 10 Maths Chapter 8 - Introduction to Trigonometry
NCERT Solutions for Exercise 8.1 Class 10 Maths Chapter 8 - Introduction to Trigonometry

NCERT solutions for exercise 8.1 Class 10 Maths chapter 8 Introduction to Trigonometry focuses on trigonometry and trigonometric ratios including sine, cosine, tangent, cosecant, secant and cotangent. 10th class Maths exercise 8.1 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1

Download PDF

Assess NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1

Introduction to Trigonometry class 10 chapter 8 Exercise: 8.1

Q1 In \Delta \: ABC , right-angled at B, AB = 24 \: cm , BC = 7 \: cm . Determine : (i)\; \sin A, \cos A (ii)\; \sin C, \cos C

Answer:

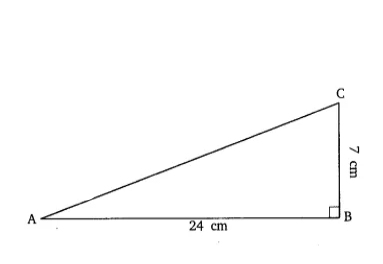
1635935005859 We have,
In \Delta \: ABC , \angle B = 90, and the length of the base (AB) = 24 cm and length of perpendicular (BC) = 7 cm
So, by using Pythagoras theorem,
\\AC^2 = AB^2 + BC^2\\ AC = \sqrt{AB^2+BC^2}
Therefore, AC = \sqrt{576+49}
AC = \sqrt{625}
AC = 25 cm

Now,
(i) \sin A = P/H = BC/AB = 7/25
\cos A = B/H = BA/AC = 24/25

(ii) For angle C, AB is perpendicular to the base (BC). Here B indicates to Base and P means perpendicular wrt angle \angle C
So, \sin C = P/H = BA/AC = 24/25
and \cos C = B/H = BC/AC = 7/25

Q2 In Fig. 8.13, find \tan P - \cot R .

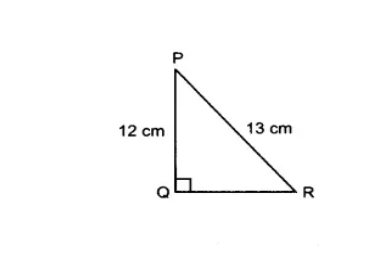
1635935041656

Answer:


We have, \Delta PQR is a right-angled triangle, length of PQ and PR are 12 cm and 13 cm respectively.
So, by using Pythagoras theorem,
QR = \sqrt{13^2-12^2}
QR = \sqrt{169-144}
QR = \sqrt{25} = 5\ cm

Now, According to question,
\tan P -\cot R = \frac{RQ}{QP}-\frac{QR}{PQ}
= 5/12 - 5/12 = 0

Q3 If \sin A=\frac{3}{4}, calculate \cos A and \tan A .

Answer:

Suppose \Delta ABC is a right-angled triangle in which \angle B = 90^0 and we have \sin A=\frac{3}{4},
So,
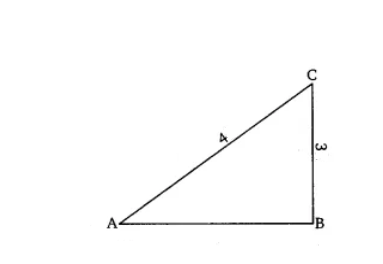
1635935058122

Let the length of AB be 4 unit and the length of BC = 3 unit So, by using Pythagoras theorem,
AB = \sqrt{16-9} = \sqrt{7} units
Therefore,
\cos A = \frac{AB}{AC} = \frac{\sqrt{7}}{4} and \tan A = \frac{BC}{AB} = \frac{3}{\sqrt{7}}

Q4 Given 15 \: \cot A=8, find \sin A and \sec A .

Answer:

We have,
15 \: \cot A=8, \Rightarrow \cot A =8/15
It implies that In the triangle ABC in which \angle B =90^0 . The length of AB be 8 units and the length of BC = 15 units

Now, by using Pythagoras theorem,
AC = \sqrt{64 +225} = \sqrt{289}
\Rightarrow AC =17 units

So, \sin A = \frac{BC}{AC} = \frac{15}{17}
and \sec A = \frac{AC}{AB} = \frac{17}{8}

Q5 Given \sec \theta =\frac{13}{12}, calculate all other trigonometric ratios.

Answer:

We have,
\sec \theta =\frac{13}{12},

It means the Hypotenuse of the triangle is 13 units and the base is 12 units.
Let ABC is a right-angled triangle in which \angle B is 90 and AB is the base, BC is perpendicular height and AC is the hypotenuse.

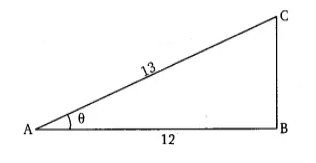
1635935082533 By using Pythagoras theorem,
BC = \sqrt{169-144}=\sqrt{25}
BC = 5 unit

Therefore,
\sin \theta = \frac{BC}{AC}=\frac{5}{13}
\cos \theta = \frac{BA}{AC}=\frac{12}{13}

\tan \theta = \frac{BC}{AB}=\frac{5}{12}

\cot \theta = \frac{BA}{BC}=\frac{12}{5}

\sec \theta = \frac{AC}{AB}=\frac{13}{12}

\csc \theta = \frac{AC}{BC}=\frac{13}{5}

Q6 If \angle A and \angle B are acute angles such that \cos A = \cos B , then show that \angle A =\angle B .

Answer:

We have, A and B are two acute angles of triangle ABC and \cos A =\cos B

sdfgjhkjhdcgv According to question, In triangle ABC,
\cos A =\cos B


\frac{AC}{AB}=\frac{BC}{AB}
\Rightarrow AC = AB
Therefore, \angle A = \angle B [angle opposite to equal sides are equal]

Q7 If \cot \theta =\frac{7}{8}, evaluate: (i)\; \frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)} (ii)\; \cot ^{2}\theta

Answer:

Given that,
\cot \theta =\frac{7}{8}
\therefore perpendicular (AB) = 8 units and Base (AB) = 7 units
Draw a right-angled triangle ABC in which \angle B =90^0
Now, By using Pythagoras theorem,
AC^2 = AB^2+BC^2
AC = \sqrt{64 +49} =\sqrt{113}

So, \sin \theta = \frac{BC}{AC} = \frac{8}{\sqrt{113}}
and \cos \theta = \frac{AB}{AC} = \frac{7}{\sqrt{113}}

\Rightarrow \cot \theta =\frac{\cos \theta}{\sin \theta} = \frac{7}{8}
(i)\; \frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}
\Rightarrow \frac{(1-\sin^2\theta)}{(1-\cos^2\theta)} = \frac{\cos^2\theta}{\sin^2\theta} = \cot ^2\theta
=(\frac{7}{8})^2 = \frac{49}{64}

(ii)\; \cot ^{2}\theta
=(\frac{7}{8})^2 = \frac{49}{64}

Q8 If 3\cot A=4, check wether \frac{1-\tan ^{2}A}{1+\tan ^{2}A}=\cos ^{2}A-\sin ^{2}A or not.

Answer:

Given that,
3\cot A=4,
\Rightarrow \cot = \frac{4}{3} = \frac{base}{perp.}
ABC is a right-angled triangle in which \angle B =90^0 and the length of the base AB is 4 units and length of perpendicular is 3 units
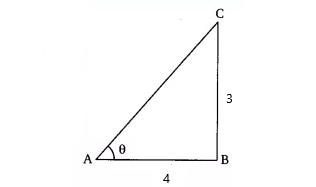
1635935097081

By using Pythagoras theorem, In triangle ABC,
\\AC^2=AB^2+BC^2\\ AC = \sqrt{16+9}\\ AC = \sqrt{25}
AC = 5 units

So,
\tan A = \frac{BC}{AB} = \frac{3}{4}
\cos A = \frac{AB}{AC} = \frac{4}{5}
\sin A = \frac{BC}{AC} = \frac{3}{5}
\frac{1-\tan ^{2}A}{1+\tan ^{2}A}=\cos ^{2}A-\sin ^{2}A
Put the values of above trigonometric ratios, we get;
\Rightarrow \frac{1-9/4}{1+9/4} = \frac{16}{25}-\frac{9}{25}
\Rightarrow -\frac{5}{13} \neq \frac{7}{25}
LHS \neq RHS

Q9 In triangle ABC , right-angled at B , if \tan A =\frac{1}{\sqrt{3}}, find the value of:

(i) \sin A\: \cos C + \cos A\: \sin C
(ii) \cos A\: \cos C + \sin A\: \sin C

Answer:

Given a triangle ABC, right-angled at B and \tan A =\frac{1}{\sqrt{3}} \Rightarrow A=30^0

FireShot%20Capture%20151%20-%20Careers360%20CMS%20-%20cms-articles%20-%20learn According to question, \tan A =\frac{1}{\sqrt{3}} = \frac{BC}{AB}
By using Pythagoras theorem,
\\AC^2 = AB^2+BC^2\\ AC = \sqrt{1+3} =\sqrt{4}
AC = 2
Now,
\\\sin A = \frac{BC}{AC} = \frac{1}{2}\\ \sin C =\frac{AB}{AC} = \frac{\sqrt{3}}{2}\\ \cos A = \frac{AB}{AC} = \frac{\sqrt{3}}{2}\\ \cos C = \frac{BC}{AC} = \frac{1}{2}

Therefore,

(i) \sin A\: \cos C + \cos A\: \sin C
\\\Rightarrow \frac{1}{2}\times\frac{1}{2}+\frac{\sqrt{3}}{2}\times \frac{\sqrt{3}}{2}\\ \Rightarrow1/4 +3/4\\ \Rightarrow4/4 = 1

(ii) \cos A\: \cos C + \sin A\: \sin C
\\\Rightarrow \frac{\sqrt{3}}{2}\times \frac{1}{2}+\frac{1}{2}\times\frac{\sqrt{3}}{2}\\ \Rightarrow \frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}\\ \Rightarrow \frac{\sqrt{3}}{2}


Q10 In \Delta \: PQR , right-angled at Q , PR + QR = 25\: cm and PQ = 5 \: cm . Determine the values of \sin P, \cos P \: and\: \tan P.

Answer:

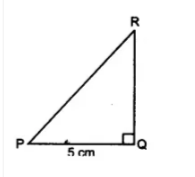
sdfghjkdfghj We have, PR + QR = 25 cm.............(i)
PQ = 5 cm
and \angle Q =90^0
According to question,
In triangle \Delta PQR,
By using Pythagoras theorem,
\\PR^2 = PQ^2+QR^2\\ PQ^2 =PR^2-QR^2 \\ 5^2= (PR-QR)(PR+QR)\\ 25 = 25(PR-QR) \\
PR - QR = 1........(ii)

From equation(i) and equation(ii), we get;
PR = 13 cm and QR = 12 cm.

therefore,
\\\sin P= \frac{QR}{PR}= 12/13\\ \cos P = \frac{PQ}{RP} = 5/13\\ \therefore \tan P = \frac{\sin P}{\cos P} = 12/5

Q11 State whether the following are true or false. Justify your answer.

(i) The value of \tan A is always less than 1.
(ii) \sec A=\frac{12}{5} for some value of angle A.
(iii) \cos A is the abbreviation used for the cosecant of angle A.
(iv) \cot A is the product of cot and A.
(v) \sin \Theta =\frac{4}{3} for some angle \Theta .

Answer:

(i) False,
because \tan 60 = \sqrt{3} , which is greater than 1

(ii) TRue,
because \sec A \geq 1

(iii) False,
Because \cos A abbreviation is used for cosine A.

(iv) False,
because the term \cot A is a single term, not a product.

(v) False,
because \sin \theta lies between (-1 to +1) [ -1\leq \sin \theta\leq 1 ]

More About NCERT Solutions for Class 10 Maths Exercise 8.1: Trigonometric Ratios

The NCERT solutions for Class 10 Maths exercise 8.1 also focused on the relationship between the trigonometric ratios. Exercise 8.1 Class 10 Maths consists of 11 questions based on trigonometric ratios and their relations. The sine is the ratio of the opposing side to the hypotenuse of a right-angle triangle.

The cosine is the ratio of the neighboring side to the hypotenuse of a right-angle triangle. The tangent is the ratio of the opposite side to the adjacent side of a right-angle triangle. The multiplicative inverse of sine is known as cosecant. Similarly, the multiplicative inverse of cosine is known as secant. The multiplicative inverse of the tangent is known as cotangent. Usage of Pythagoras theorem is also covered in exercise 8.1 Class 10 Maths. Students can use these Introduction to Trigonometry Class 10 notes to quick revision of the important concepts discussed in this chapter.

Benefits of NCERT Solutions for Class 10 Maths Exercise 8.1:

  • NCERT solutions for Class 10 Maths exercise 8.1 are important for first and second term exams as well as for higher grades. We should practice all the questions present in NCERT solutions for Class 10 Maths exercise 8.1 twice or thrice to attain good and high marks.
  • Exercise 8.1 Class 10 Maths, Trigonometric ratios are used in finding the missing sides or angles of the right-angle triangle.
  • By solving the NCERT solution for Class 10 Maths chapter 8 exercise 8.1 exercises, students can do any type of questions related to trigonometry easily by exploring the derivation of these formulas.

Also, see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What are the three basic trigonometric ratios according to NCERT solutions for Class 10 Maths chapter 8 exercise 8.1 ?

The three basic trigonometric ratios are sine, cosine and tangent. 

2. What is the sine function and write it’s formula?

The ratio of the opposite side to the hypotenuse of the right angle triangle is known as the sine.

Sin θ=opposite side/hypotenuse 

3. What is Cos ?

Cos means Cosine is the ratio of Adjacent Side and Hypotenuse

4. What is the relationship between sine, cosine and tangent functions ?

tan θ=sin θ/cos θ

5. What is the relationship between sine and cosecant functions ?

The multiplicative inverse of sine is known as the cosecant

6. What are the six trigonometric ratios according to NCERT solutions for Class 10 Maths chapter 8 exercise 8.1 ?

The six trigonometric ratios are 

  • Sine 

  • Cosine 

  • Tangent 

  • Cotangent 

  • Cosecant  

  • Secant.

7. How many questions and what type of questions are there in the NCERT solutions for Class 10 Maths chapter 8 exercise 8.1 ?

NCERT solutions for Class 10 Maths chapter 8 exercise 8. 1 consists of 11 Questions in which 7 are short answers, 3 of them are long answers and the remaining one is a short answer with reasoning and all the questions are based on trigonometric ratios. 

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 812 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
IBM
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
15 hours ago :
October 23, 2024 - 04:01 PM IST :
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST
CBSE conducts surprise inspections at 27 schools in Rajasthan, Delhi to curb menace of dummy schools
September 03, 2024 - 03:02 PM IST

Stay up-to date with CBSE Class 10th News

Back to top