JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
NCERT Solutions for Exercise 15.1 Class 9 Maths Chapter 15 - Probability
Edited By Sumit Saini | Updated on Jul 06, 2022 02:49 PM IST
A probability is a number that reflects the chance or likelihood that a particular event will occur. In this NCERT book class 9 chapter we will be studying a few basics of probability. Over to exercise 15.1 Class 9 Maths is an Introductory exercise covers the round ups after solved examples. Studying and understanding their concepts helps them to score more. In this NCERT exercise 15.1, we will be studying overall new concepts, Like chances of happening of event in values and percentage-wise. In chapter 15 of Class 9 NCERT Mathematics, the exercise initiates with questions related to calculating odds and happening of that particular event using basic definition of probability and rest questions will be solved using examples mentioned with chapter.
This Story also Contains
- Probability Class 9 Maths Chapter 15 Exercise: 15.1
- More About NCERT Solutions for Class 9 Maths Chapter 15 Exercise 15.1
- Benefits of NCERT Solutions for Class 9 Maths Chapter 15 Exercise 15.1
- NCERT Solutions of Class 10 Subject Wise
The NCERT syllabus Class 9 Maths chapter 15 exercise 15.1 is very basic level exercise to give a glance to students how Probability works and its concepts of which counts us on starting questions based on observations, maximum and minimum predicted values and many more. This chapter introduce us with real-life along with explanation of each problem detailed in NCERT Solutions for Class 9 Maths Chapter 15 exercise 15.1. Along with Class 9 Maths Chapter 1 exercise 15.1 the following exercises are also present.
Probability Class 9 Maths Chapter 15 Exercise: 15.1
Answer:
From the above question, the data of interest is,
Total Number of balls batswoman played = 30
Number of times batswoman hits a boundary =6
Therefore, we can say,
Number of times batswoman could not hit a boundary =24
P(she did not hit a boundary)
=24/30 =0.80
Ans:0.80
| Number of girls in a family | 2 | 1 | 0 |
| Number of families | 475 | 814 | 211 |
Answer:
From the above question, the data that we can take is,
Total Number of families= 475+814+211 = 1500
Number of families having 2 girls in the family =475
We know:
Empirical (or experimental) probability P(E) of this event can be written as
P(Family, chosen at random has 2 girls) =
= 475/1500 = 19/60
| Number of girls in a family | 2 | 1 | 0 |
| Number of families | 475 | 814 | 211 |
Answer:
From the above question, the data that we can take is,
Total Number of families= 475+814+211 = 1500
Number of families having 1 girl in the family =814
We know:
Empirical (or experimental) probability P(E) of this event can be written as
P(Family, chosen at random has 1 girl) =
= 814/1500 = 407/1500
| Number of girls in a family | 2 | 1 | 0 |
| Number of families | 475 | 814 | 211 |
Answer:
From the above question, the data that we can take is,
Total Number of families= 475+814+211 = 1500
Number of families having no girls in the family =211
We know:
Empirical (or experimental) probability P(E) of this event can be written as
P(Family, chosen at random has no girls) =
= 211/1500
Ans:= 211/1500
Answer:
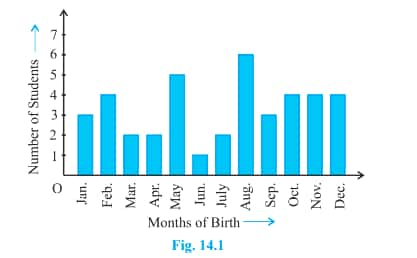
Total no. of students = 40
Total no. of students who all are born in August =6
P( a student of the class was born in August) =6/40
=3/20
Ans : 3/20
Outcome | 3 Heads | 2 Heads | 1 Head | 0 Head |
Frequencies | 23 | 72 | 77 | 28 |
Answer
Total number of times coins tossed = 200
Total number of possible outcomes = 72
Required probability = 72/200 => 9/25
Suppose a family is chosen. Find the probability that the family chosen is earning ` Rs. 10000 – Rs.13000 per month and owning exactly 2 vehicles.
| Monthly income (in Rs) | Vehicles per family | |||
| 0 | 1 | 2 | Above 2 | |
| Less than 7000 | 10 | 160 | 25 | 0 |
| 7000-10000 | 0 | 305 | 27 | 2 |
| 10000-13000 | 1 | 535 | 29 | 1 |
| 13000-16000 | 2 | 469 | 59 | 25 |
| 16000 or more | 1 | 579 | 82 | 88 |
Answer:
Although it is given that,
Total no. of families= 2400
Let us find this by adding all the cases
= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400
Earning Rs. 10000 – Rs.13000 per month and owning exactly 2 vehicles =29
P(Earning Rs. 10000–Rs.13000 per month and owning exactly 2 vehicles)= P 1
P 1 = 29/2400
| Monthly income (in Rs) | Vehicles per family | |||
| 0 | 1 | 2 | Above 2 | |
| Less than 7000 | 10 | 160 | 25 | 0 |
| 7000-10000 | 0 | 305 | 27 | 2 |
| 10000-13000 | 1 | 535 | 29 | 1 |
| 13000-16000 | 2 | 469 | 59 | 25 |
| 16000 or more | 1 | 579 | 82 | 88 |
Suppose a family is chosen. Find the probability that the family chosen is earning Rs.16000 or more per month and owning exactly 1 vehicle.
Answer:
Although it is given that,
Total no. of families= 2400
Let us find by this adding all the cases
= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400
Total no. of families earning Rs.16000 or more per month and owning exactly 1 vehicle = 579
P(earning Rs.16000 or more per month and owning exactly 1 vehicle )= P2
P2 = 579/2400
| Monthly income (in Rs) | Vehicles per family | |||
| 0 | 1 | 2 | Above 2 | |
| Less than 7000 | 10 | 160 | 25 | 0 |
| 7000-10000 | 0 | 305 | 27 | 2 |
| 10000-13000 | 1 | 535 | 29 | 1 |
| 13000-16000 | 2 | 469 | 59 | 25 |
| 16000 or more | 1 | 579 | 82 | 88 |
Suppose a family is chosen. Find the probability that the family chose is earning less than Rs. 7000 per month and does not own any vehicle.
Answer:
Although it is given that,
Total no. of families= 2400
Let us find by this adding all the cases
= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400
Total no. of families, those are earning less than Rs. 7000 per month and not having any vehicle = 10
P(earning less than Rs. 7000 per month and does not have any vehicle)= P3
P3 = 10/2400
=1/240
Ans: 1/240
| Monthly income (in Rs) | Vehicles per family | |||
| 0 | 1 | 2 | Above 2 | |
| Less than 7000 | 10 | 160 | 25 | 0 |
| 7000-10000 | 0 | 305 | 27 | 2 |
| 10000-13000 | 1 | 535 | 29 | 1 |
| 13000-16000 | 2 | 469 | 59 | 25 |
| 16000 or more | 1 | 579 | 82 | 88 |
Suppose a family is chosen. Find the probability that the family chose is earning `Rs.13000 – 16000 per month and owning more than 2 vehicles.
Answer:
Although it is given that,
Total no. of families= 2400
Let us find by this adding all the cases
= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400
Total number of families,those are earning Rs.13000 – 16000 per month and owning more than 2 vehicles = 25
P(earning Rs.13000 – 16000 per month and owning more than 2 vehicles)= P4
P4 = 25/2400
=1/96
Ans :1/96
| Monthly income (in Rs) | Vehicles per family | |||
| 0 | 1 | 2 | Above 2 | |
| Less than 7000 | 10 | 160 | 25 | 0 |
| 7000-10000 | 0 | 305 | 27 | 2 |
| 10000-13000 | 1 | 535 | 29 | 1 |
| 13000-16000 | 2 | 469 | 59 | 25 |
| 16000 or more | 1 | 579 | 82 | 88 |
Suppose a family is chosen. Find the probability that the family chosen is owning not more than 1 vehicle.
Answer:
Although it is given that,
Total no. of families= 2400
Let us find by this adding all the cases
= 10+0+1+2+1+160+305+535+469+579+25+27+29+59+82+0+2+1+25+88 =2400
Total number of families owning not more than 1 vehicle= 10+0+1+2+1+160+305+535+469+579 = 2062
Let, P(families owning not more than 1 vehicle)= P5
P5 = 2062/2400
Answer:
| Marks | Number of students |
| 0-20 | 2 |
| 20-30 | 10 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 20 |
| 60-70 | 15 |
| 70- above | 8 |
| Total | 90 |
From the above question, the data of our interest is:
Total no. of students =90
Total no. of students who obtained less than 20% in the mathematics test= 7
P(student obtained less than 20% in the mathematics test) = 7/90
Ans: 7/90
Q6 (ii) Refer to Table 14.7, Chapter 14. Find the probability that a student obtained marks 60 or above.
Answer:
| Marks | Number of students |
| 0-20 | 2 |
| 20-30 | 10 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 20 |
| 60-70 | 15 |
| 70- above | 8 |
| Total | 90 |
From the above question, the data of our interest is:
Total no. of students =90
Total no. of students who obtained marks 60 or above = 15+8 =23
P(a student obtains marks 60 or above) = 23/90
Ans: 23/90
| Opinion | Number of students |
| like | 135 |
| dislike | 65 |
Find the probability that a student is chosen at random likes statistics,
Answer:
From the above question, the data of our interest is:
Total no. of students =135+65 =200
Total no. of students who like statistics = 135
P(students like statistics )= 135/200 =27/40
Ans: 27/40
| Opinion | Number of students |
| like | 135 |
| dislike | 65 |
Find the probability that a student chosen at random does not like it.
Answer:
From the above question, the data of our interest is:
Total no. of students =135+65=200
Total no. of students who do not like it.= 65
P(a student does not like it) = 65/200
= 13/40
Ans: 13/40
Answer:
The distance (in km) of 40 engineers from their residene to their place of work were found as follows:
| 5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
| 19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
| 7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
| 12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Total no. of engineers = 40
Total no. of engineers who are living less than 7 km from their workplace = 9
Therefore we can say,
P(engineers who are living less than 7 km from their workplace)=
= 9/40
Ans: 9/40
Answer:
The distance (in km) of 40 engineers from their residene to their place of work were found as follows:
| 5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
| 19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
| 7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
| 12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Total no. of engineers = 40
Total no. of engineers who are living less than 7 km from their workplace = 31
Therefore we can say,
P(engineers who are living more than or equal to 7 km from their workplace)=31/40
Ans: 31/40
Answer:
The distance (in km) of 40 engineers from their residene to their place of work were found as follows:
| 5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
| 19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
| 7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
| 12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Hey, don't you think its too simple:
Well, there is no such engineer whose distance between residence and place of work is less than 1/2 km
Therefore,
engineer whose distance between residence and place of work is less than 1/2 km =0
P(engineer whose distance between residence and place of work is less than 1/2 km) = 0
Ans: 0
Answer:
This activity can be taken as a general problem:
Assumption:
Let the frequency of two-wheelers = x
Let the frequency of three-wheelers = y
Let the frequency of four-wheelers = z
Total no. of vehicles= x+y+z
therefore,
P(anyone vehicle out of the total vehicles I have observed is a two-wheeler) =
Answer:
This activity can be taken as a general problem:
Well, we know the divisibility by 3 is when the sum of all the digits is divisible by 3
So,
The student will write the number between 100-999
There are 900 3 - digit numbers , which are 100, 101, 102, 103, ..., 999.
The first 3-digit numbers that are exactly divisible by 3 is 102, 105, ..... 999
total numbers which are divisible by 3 = 300
P(the sum of all the digits is divisible by 3) = 300/900
=1/3
Ans: 1/3
Answer:
From the above question, the data of our interest is:
Total no. of bags = 11
Total no. of bags that contain more than 5 kg flour = 7
P(Bag contain more than 5 kg flour) = 7/11
Ans: 7/11
Answer:
The data is representing the concentration of sulfur dioxide in the air in parts per million (ppm) of a city. The data obtained for a month of 30 days is as follows:
| 0.03 | 0.08 | 0.08 | 0.09 | 0.04 | 0.17 |
| 0.16 | 0.05 | 0.02 | 0.06 | 0.18 | 0.20 |
| 0.11 | 0.08 | 0.12 | 0.13 | 0.22 | 0.07 |
| 0.08 | 0.01 | 0.10 | 0.06 | 0.09 | 0.18 |
| 0.11 | 0.07 | 0.05 | 0.07 | 0.01 | 0.04 |
Total no. of days =30
No. of days in which Conc. of sulfur dioxide in the interval 0.12 - 0.16 = 2
P(Conc. of sulphur dioxide in the interval 0.12 - 0.16) =2/30
Ans: 1/15
Answer:
The below-written data is representing the blood groups of 30 students study in class VIII.
A, B, O, O, B, A, O, O, AB, O, A, O, B, A, O
A, AB, O, A, A, B, A, B, O, O, O, AB, B, A, O
Total no. of students = 30
Total no. of students of this class who has blood group AB =3
P(Student of this class has blood group AB)= 3/30 => 1/10
Ans: 1/10
More About NCERT Solutions for Class 9 Maths Chapter 15 Exercise 15.1
Rest details of exercise 15.1 Class 9 Maths. Consist of normal probability problems based on the formula itself. As the problem number increases, the probability gets connection with statistics as in the analysis of data covered NCERT solutions for Class 9 Maths chapter 15 exercise 15.1. In the lasts of Class 9 Maths chapter 15 exercise, 15.1 shifting of probability to an interpretation of data gives a finite touch to best of Probability The Class 9 Maths chapter 15 exercise 15.1 gives attributes to classical theory problems in this chapter.
Also Read| Probability Class 9 Notes
Benefits of NCERT Solutions for Class 9 Maths Chapter 15 Exercise 15.1
Number one benefit of studying this exercise 15.1 Class 9 Maths is that Probability is one of the finest chapters whose existence gets repeated again and again and If we talk especially about NCERT solutions for Class 9 Maths chapter 15 exercise 15.1 solution of all the Numerical problems are there, which makes it easy to work on
Another benefit is Probability is easy to understand and scoring exercise in Class 9 Maths chapter 15 exercise 15.1
One last benefit of Class 9 Maths chapter 15 exercise 15.1 is that most short answers and MCQ comprise this chapter and exercise hence it would be easy for students to work on
Also, see-
NCERT Solutions of Class 10 Subject Wise
Frequently Asked Questions (FAQs)
1. What do you mean by chance?
Ans: An experiment is a well designed procedure that is carried out under strict supervision. The experiment is considered to be a chance if the outcome isn't known ahead of time.
2. What do you mean Formula of Probability?
Ans: P = n(a)/n(s) n(a) = number of favorable outcomes , n(s) = total number of outcomes
3. What is Equally-Likely Event in probability with one example?
Ans: Equally probable suggests that each experimental outcome has an equal chance of occurring. If you toss a fair, six-sided die, each face (1, 2, 3, 4, 5, and 6) has the same chance of appearing as the others.
4. What is of Impossible event?
Ans: The probability of impossible event is 0
5. In sample space s if P(a) = 0 then is A is an independent of any other event?
Ans: P(a) =0 that means it is an impossible event hence
A is not dependent on any other event
6. What is probability of happening of two event simultaneously according to set theory?
Ans: . P(AUB) = P(A) + P(B) – P(AB)
7. What is Mutually Exclusive events?
Ans: If two occurrences do not occur at the same time in probability theory, they are mutually exclusive or disjoint. The set of outcomes of a single coin toss, which can result in either heads or tails but not both, is a good example.
8. What is the expression of P(AUB) when both the events are mutually exclusive?
Ans: For mutually exclusive events P(AB) = 0
Hence expression is P(AUB) = P(A) + P(B).
Also Read
Articles
Get answers from students and experts
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Popular Course After 12th
Applications for Admissions are open.
JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
TOEFL ® Registrations 2024
ApplyAccepted by more than 11,000 universities in over 150 countries worldwide
Pearson | PTE
ApplyTrusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK
JEE Main high scoring chapters and topics
ApplyAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
ApplyAs per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
News and Notifications
Back to top