Aakash Repeater Courses
ApplyTake Aakash iACST and get instant scholarship on coaching programs.
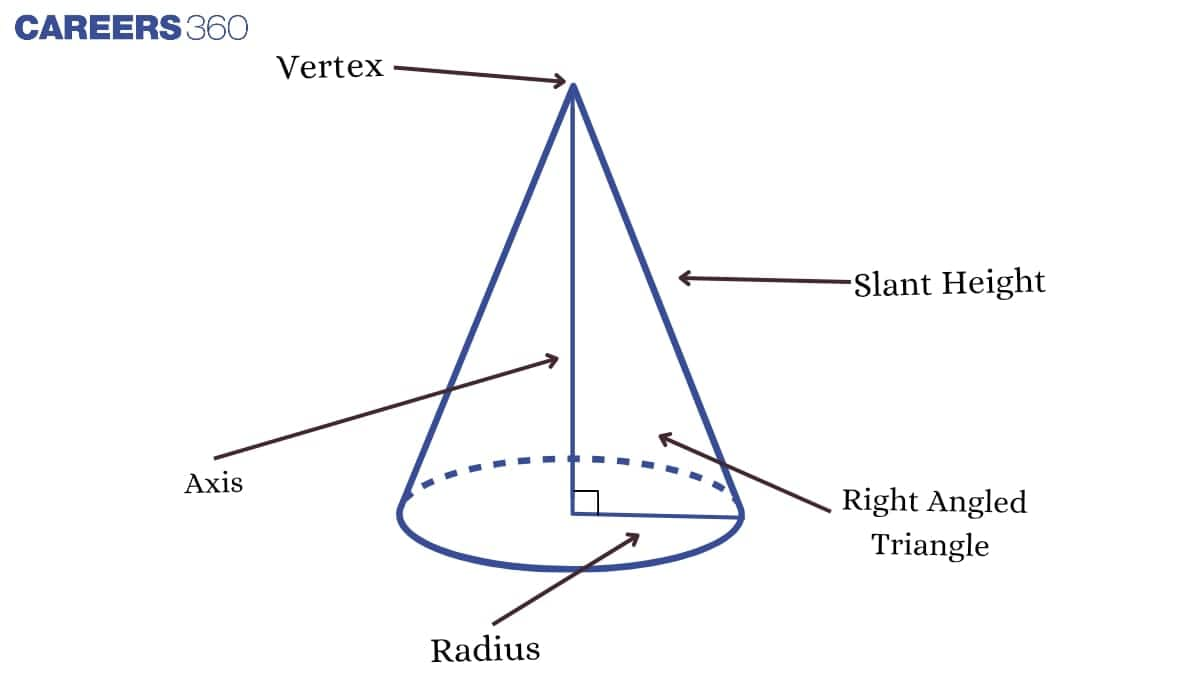
NCERT Solutions for Class 9 Maths exercise 11.1 deals with the concept of the right circular cone and its surface areas. A three-dimensional shape which narrows smoothly from a flat base to a point is known as a cone. Mathematically, there are two types of cones, namely the right circular cone and the oblique cone. A type of cone whose axis falls perpendicular to the plane of the base is known as the right circular cone. The distance from the vertex or apex to the point on the outer line of the circular base of the cone is known as the slant height, which is derived from the Pythagorean Theorem. The formula for calculating the slant height of the right circular cone is l2 = r2 + h2; from the formula, l can be calculated. The surface area of a right circular cone is the area covered by the surface of the right circular cone. Surface area can be divided into two categories. They are
Don't Miss: Best Courses after 10th | Competitive Exams after 10th

The curved surface area of the right circular cone, also known as the lateral surface area of the right circular cone, is the area covered by the curved surface of the cone. The total surface area of the right circular cone is the area occupied by the complete cone. NCERT solutions for Class 9 Maths chapter 11 exercise 11.1 include eight questions, according to the NCERT Books, seven of which are simple, and the remaining one may take some time to complete. This Class 9 Maths chapter 11 exercise 11.1 thoroughly explains the concepts of surface area and volume. Our Subject Matter Expert created the NCERT Solutions in an easy and understandable language.
** As per the CBSE Syllabus for 2023-24, please note that this chapter has been renumbered as Chapter 11.
Answer:
Given,
Base diameter of the cone = d=10.5 cm
Slant height = l=10 cm
We know, Curved surface area of a cone =πrl
∴ Required curved surface area of the cone=
=227×10.52×10=165 cm2
Q2 Find the total surface area of a cone, if its slant height is 21m and diameter of its base is 24m .
Answer:
Given,
Base diameter of the cone = d=24 m
Slant height = l=21 cm
We know, Total surface area of a cone = Curved surface area + Base area
=πrl+πr2=πr(l+r)
∴ Required total surface area of the cone=
=227×242×(21+12)=227×242×33=1244.57 m2
Q3 (i) Curved surface area of a cone is 308cm2 and its slant height is 14 cm. Find radius of the base .
Answer:
Given,
The curved surface area of a cone = 308cm2
Slant height =l=14 cm
(i) Let the radius of cone be r cm
We know, the curved surface area of a cone= πrl
∴ πrl=308⇒227×r×14=308⇒r=30844=7
Therefore, the radius of the cone is 7 cm
Answer:
Given,
The curved surface area of a cone = 308cm2
Slant height =l=14 cm
The radius of the cone is r= 7 cm
(ii) We know, Total surface area of a cone = Curved surface area + Base area
=πrl+πr2
=308+227×72=308+154=462 cm2
Therefore, the total surface area of the cone is 462 cm2
Q4 (i) A conical tent is 10 m high and the radius of its base is 24 m. Find slant height of the tent.
Answer:
Given,
Base radius of the conical tent = r=24 m
Height of the conical tent = h=10 m
∴ Slant height = l=h2+r2
=102+242=676=26 m
Therefore, the slant height of the conical tent is 26 m
Answer:
Given,
Base radius of the conical tent = r=24 m
Height of the conical tent = h=10 m
∴ Slant height = l=h2+r2=26 m
We know, Curved surface area of a cone =πrl
∴ Curved surface area of the tent
=227×24×26=137287 m2
Cost of 1 m2 of canvas = Rs. 70
∴ Cost of 137287 m2 of canvas =
Rs. (137287×70)=Rs. 137280
Therefore, required cost of canvas to make tent is Rs. 137280
Answer:
Given,
Base radius of the conical tent = r=6 m
Height of the tent = h=8 m
We know,
Curved surface area of a cone = πrl=πrh2+r2
∴ Area of tarpaulin required = Curved surface area of the tent
=3.14×6×82+62=3.14×6×10=188.4 m2
Now, let the length of the tarpaulin sheet be x m
Since 20 cm is wasted, effective length = x−20cm=(x−0.2) m
Breadth of tarpaulin = 3 m
∴[(x−0.2)×3]=188.4⇒x−0.2=62.8⇒x=63 m
Therefore, the length of the required tarpaulin sheet will be 63 m.
Answer:
Given, a conical tomb
The base diameter of the cone = d=14 m
Slant height =l=25 m
We know, Curved surface area of a cone =πrl
=227×142×25=22×25=550 m2
Now, Cost of whitewashing per 100m2 = Rs. 210
∴ Cost of whitewashing per 550m2 = Rs.(210100×550)
=Rs. (21×55)=Rs. 1155
Therefore, the cost of white-washing its curved surface of the tomb is Rs. 1155 .
Answer:
Given, a right circular cone cap (which means no base)
Base radius of the cone = r=7 cm
Height =h=24 cm
∴l=h2+r2
We know, Curved surface area of a right circular cone =πrl
∴ The curved surface area of a cap =
=227×7×242+72=22×625=22×25 =550 cm2
∴ The curved surface area of 10 caps = 550×10=5500 cm2
Therefore, the area of the sheet required for 10 caps = 5500 cm2
Answer:
Given, hollow cone.
The base diameter of the cone = d=40 cm=0.4 m
Height of the cone = h=1 m
∴ Slant height = l=h2+r2 =12+0.22
We know, Curved surface area of a cone = πrl=πrh2+r2
∴ The curved surface area of 1 cone = 3.14×0.2×1.04=3.14×0.2×1.02
=0.64056 m2
∴ The curved surface area of 50 cones =(50×0.64056) m2
=32.028 m2
Now, the cost of painting 1 m2 area = Rs. 12
∴ Cost of the painting 32.028 m2 area =Rs. (32.028×12)
=Rs. 384.336
Therefore, the cost of painting 50 such hollow cones is Rs. 384.34 (approx)
Also Read:
The NCERT solutions for Class 9 Maths exercise 11.1 is mainly focused on the surface area of the right circular cone. In exercise 11.1, Class 9 Maths, the curved surface area of a cone can be calculated by multiplying the area of the sector by the radius length. The area of the lateral surface plus the area of the circular base equals the total surface area of a closed right circular cone. V=13πr2h is the volume of a right circular cone, which is one-third of the product of the circular base's area and its height. Surface areas are measured in square units, but the volume of a cube is measured in cubic units.
Also See:
Students must check the NCERT solutions for Class 9 Maths and Science given below:
Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:
According to NCERT solutions for Class 9 Maths chapter 13 exercise 11.1 , A type of cone whose axis falls perpendicular on the plane of the base is known as the right circular cone.
The point formed at the end of the cone is known as the apex .
A cone has only one apex .
The total surface area of the cone is πr(l + r)
In the right cone, there are two surfaces. There are two types of surfaces: base and slanted surfaces .
The total surface area of a closed right circular cone is computed by adding the area of the lateral surface and the area of the circular base.

Take Aakash iACST and get instant scholarship on coaching programs.

This ebook serves as a valuable study guide for NEET 2025 exam.

This e-book offers NEET PYQ and serves as an indispensable NEET study material.

As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
As per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE