NCERT Solutions for Exercise 1.5 Class 9 Maths Chapter 1

NCERT Solutions for Exercise 1.5 Class 9 Maths Chapter 1 - Number Systems

Edited By Vishal kumar | Updated on Sep 30, 2023 10:14 AM IST

NCERT Solutions for Class 9 Maths Chapter 1: Number Systems Exercise 1.5- Download Free PDF

NCERT Solutions Class 9 Maths Chapter 1 Number Systems Exercise 1.5- NCERT Solutions for Class 9 Maths exercise 1.5 deals with the concepts of the type of numbers into rational and irrational numbers and also the use of certain mathematical operations. Mathematically, numbers are labelled into many units, particularly rational numbers, irrational numbers, natural numbers, whole numbers, integers and real numbers. Real numbers, as defined in exercise 1.5 Class 9 Maths are the combination of rational and irrational numbers, which might have positive or negative attributes. A number that can be broken down into parts and addressed as p/q where p and q are integers and q≠0 are rational numbers. Irrational numbers are numbers that can't be stated as a fraction with a number in the numerator and denominator.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions for Class 9 Maths Chapter 1: Number Systems Exercise 1.5- Download Free PDF
NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems Exercise 1.5
Access Number Systems Class 9 Chapter 1 Exercise: 1.5
More About NCERT Solutions for Class 9 Maths Exercise 1.5:
Benefits of NCERT Solutions for Class 9 Maths Exercise 1.5:
Key Features of class 9 maths chapter 1 exercise 1.5
NCERT Solutions of Class 10 Subject Wise
Subject Wise NCERT Exemplar Solutions

NCERT Solutions for Exercise 1.5 Class 9 Maths Chapter 1 - Number Systems

NCERT solutions for Class 9 Maths Chapter 1 exercise 1.5 includes five questions where four are lengthy and the remaining 1 among them is the brief solution which is based on the category of determining the numbers into rational and irrational numbers by using certain mathematical operations and the illustration of given numbers on the number line. The concepts associated with the number lines and mathematical operations are nicely defined in this Class 9 Maths chapter 1 exercise 1.5. The following exercises are also present along with Class 9 Maths Chapter 1 exercise 1.5.

The 9th class maths exercise 1.5 answers are authored by subject experts in straightforward language, ensuring ease of understanding. Additionally, they are accessible in PDF format, allowing students to download and utilize them conveniently.

NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems Exercise 1.5

Download PDF

Access Number Systems Class 9 Chapter 1 Exercise: 1.5

Q1 (i) Classify the following numbers as rational or irrational: $2-\sqrt{5}$

Answer:

Value of $\sqrt{5}$ is 2.23606798....
Now,
$\Rightarrow 2 - \sqrt{5} = 2 - 2.23606798... = -0.23606798...$
Now,
Since the number is in non-terminating non-recurring. Therefore, it is an irrational number.

Q1 (ii) Classify the following numbers as rational or irrational: $\left ( 3+\sqrt{23} \right )-\sqrt{23}$

Answer:

Given number is $\left ( 3+\sqrt{23} \right )-\sqrt{23}$

$\Rightarrow \left ( 3+\sqrt{23} \right )-\sqrt{23} = 3+\sqrt{23}-\sqrt{23} = 3$
Now, it is clearly a rational number because we can represent it in the form of $\frac{p}{q}$

Q1 (iii) Classify the following numbers as rational or irrational: $\frac{2\sqrt{7}}{7\sqrt{7}}$

Answer:

Given number is $\frac{2\sqrt{7}}{7\sqrt{7}}$

$\Rightarrow \frac{2\sqrt{7}}{7\sqrt{7}} = \frac{2}{7}$
As we can clearly see that it can be represented in $\frac{p}{q}$ form. Therefore, it is a rational number.

Q1 (iv) Classify the following numbers as rational or irrational: $\frac{1}{\sqrt{2}}$

Answer:

Given number is $\frac{1}{\sqrt{2}}$

$\Rightarrow \frac{1}{\sqrt{2}}= \frac{\sqrt{2}}{2}=\frac{1.41421356..}{2} =0.7071068...$
Now,
Clearly, as the decimal expansion of this expression is non-terminating and non-recurring. Therefore, it is an irrational number.

Q1 (v) Classify the following numbers as rational or irrational: $2\pi$

Answer:

Given number is $2\pi$
We know that the value of $\pi = 3.14159265...$
Now,
$\Rightarrow 2\pi = 2\times 3.14159265... = 6.2831853...$
Now,
Clearly, as the decimal expansion of this expression is non-terminating and non-recurring. Therefore, it is an irrational number.

Q2 (i) Simplify each of the following expressions: $(3+\sqrt{3})(2+\sqrt{2})$

Answer:

Given number is $(3+\sqrt{3})(2+\sqrt{2})$
Now, we will reduce it into
$\Rightarrow (3+\sqrt{3})(2+\sqrt{2})= 3.2+3.\sqrt{2}+\sqrt{3}.2+\sqrt{3}.\sqrt{2}$
$= 6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}$

Therefore, answer is $6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}$

Q2 (ii) Simplify each of the following expressions: $\left (3+\sqrt{3} \right )\left ( 3-\sqrt{3} \right )$

Answer:

Given number is

$\left (3+\sqrt{3} \right )\left ( 3-\sqrt{3} \right )$
Now, we will reduce it into
$\Rightarrow (3+\sqrt{3})(3-\sqrt{3})= \left ( (3)^2-(\sqrt{3})^2 \right )$ $\left ( using \ (a+b)(a-b)=a^2-b^2 \right )$
$=9 - 3 = 6$

Therefore, answer is 6

Q2 (iii) Simplify each of the following expressions: $\left (\sqrt{5}+\sqrt{2} \right )^{2}$

Answer:

Given number is $\left (\sqrt{5}+\sqrt{2} \right )^{2}$

Now, we will reduce it into
$\Rightarrow \left (\sqrt{5}+\sqrt{2} \right )^{2} = \left ( (\sqrt{5})^2+(\sqrt{2})^2+2.\sqrt{5}.\sqrt{2} \right )$ $\left ( using \ (a+b)^2=a^2+b^2 +2ab\right )$
$=5+2+2\sqrt{10}$
$=7+2\sqrt{10}$

Therefore, the answer is $7+2\sqrt{10}$

Q2 (iv) Simplify each of the following expressions: $\left (\sqrt{5}-\sqrt{2} \right )\left ( \sqrt{5}+\sqrt{2} \right )$

Answer:

Given number is $\left (\sqrt{5}-\sqrt{2} \right )\left ( \sqrt{5}+\sqrt{2} \right )$

Now, we will reduce it into
$\Rightarrow \left (\sqrt{5}-\sqrt{2} \right )\left ( \sqrt{5}+\sqrt{2} \right )= \left ( (\sqrt{5})^2-(\sqrt{2})^2 \right )$ $\left ( using \ (a+b)(a-b)=a^2-b^2\right )$
$=5-2$
$=3$

Therefore, the answer is 3 .

Q3 Recall, $\pi$ is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, $\pi=\frac{c}{d}$ ⋅ This seems to contradict the fact that $\pi$ is irrational. How will you resolve this contradiction?

Answer:

There is no contradiction.
When we measure a length with scale or any other instrument, we only obtain an approximate rational value. We never obtain an exact value.
For this reason, we cannot say that either c or d is irrational.
Therefore, the fraction $\frac{c}{d}$ is irrational. Hence, the value of $\pi$ is approximately equal to $\frac{22}{7} = 3.142857....$

Therefore, $\pi$ is irrational.

Q4 Represent $\sqrt{9.3}$ on the number line.

Answer:

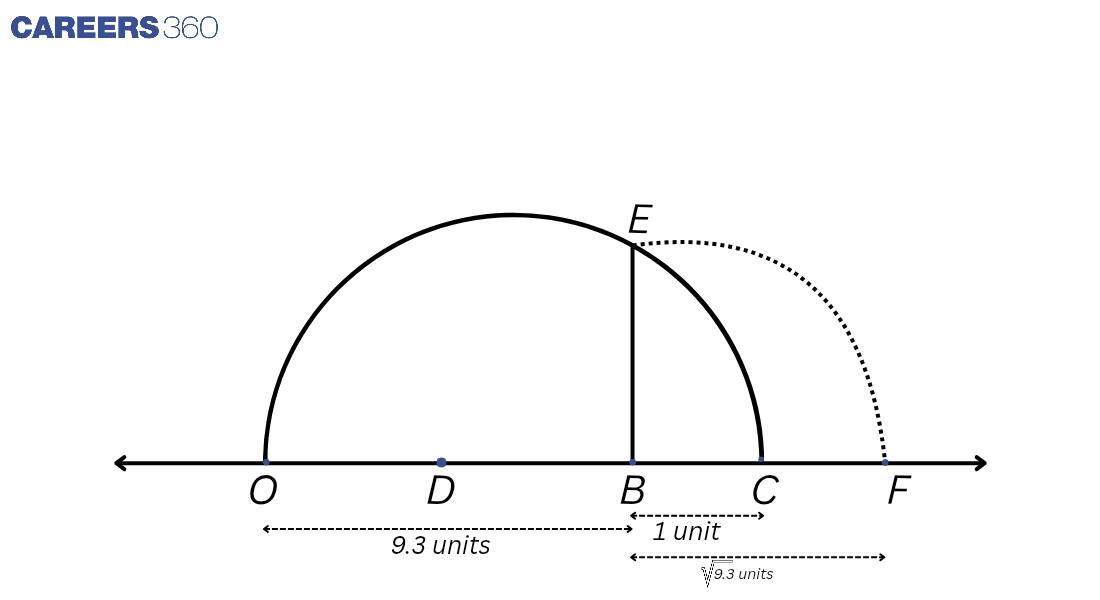
1639723609742 Draw a line segment OB of 9.3 unit. Then, extend it to C so that BC = 1 unit. Find the mid-point D of OC and draw a semi-circle on OC while taking D as its centre and OD as the radius. Now, Draw a perpendicular to line OC passing through point B and intersecting the semi-circle at E. Now, Take B as the centre and BE as radius, draw an arc intersecting the number line at F. the length BF is $9\sqrt{3}$ units.

Q5 (i) Rationalise the denominators of the following: $\frac{1}{\sqrt{7}}$

Answer:

Given number is $\frac{1}{\sqrt{7}}$

Now, on rationalisation, we will get

$\Rightarrow \frac{1}{\sqrt 7} = \frac{1}{\sqrt 7}\times \frac{\sqrt 7}{\sqrt 7 } = \frac{\sqrt7}{7}$

Therefore, the answer is $\frac{\sqrt7}{7}$

Q5 (ii) Rationalise the denominators of the following: $\frac{1}{\sqrt{7}-\sqrt{6}}$

Answer:

Given number is $\frac{1}{\sqrt{7}-\sqrt{6}}$

Now, on rationalisation, we will get

$\Rightarrow \frac{1}{\sqrt 7-\sqrt6} = \frac{1}{\sqrt 7-\sqrt 6}\times \frac{\sqrt 7+\sqrt 6 }{\sqrt 7+\sqrt 6 } = \frac{\sqrt7+\sqrt 6}{(\sqrt7)^2-(\sqrt6)^2} = \frac{\sqrt7+\sqrt6}{7-6}$ $= \sqrt7+\sqrt6$

Therefore, the answer is $\sqrt7+\sqrt6$

Q5 (iii) Rationalise the denominators of the following: $\frac{1}{\sqrt{5}+\sqrt{2}}$

Answer:

Given number is $\frac{1}{\sqrt{5}+\sqrt{2}}$

Now, on rationalisation, we will get

$\\= \frac{1}{\sqrt 5+\sqrt2} \\\\= \frac{1}{\sqrt 5+\sqrt 2}\times \frac{\sqrt 5-\sqrt 2 }{\sqrt 5-\sqrt 2 }\\\\ = \frac{\sqrt5-\sqrt 2}{(\sqrt5)^2-(\sqrt2)^2} \\\\= \frac{\sqrt5-\sqrt2}{5-2}$
$= \frac{\sqrt5-\sqrt2}{3}$

Therefore, the answer is $\frac{\sqrt5-\sqrt2}{3}$

Q5 (iv) Rationalise the denominators of the following: $\frac{1}{\sqrt{7}-2}$

Answer:

Given number is $\frac{1}{\sqrt{7}-2}$

Now, on rationalisation, we will get

$\Rightarrow \frac{1}{\sqrt 7-2} = \frac{1}{\sqrt 7- 2}\times \frac{\sqrt 7+ 2 }{\sqrt 7+ 2 } = \frac{\sqrt7+ 2}{(\sqrt7)^2-(2)^2} = \frac{\sqrt7+2}{7-4}$
$= \frac{\sqrt7+2}{3}$

Therefore, the answer is $\frac{\sqrt7+2}{3}$

Benefits of NCERT Solutions for Class 9 Maths Exercise 1.5:

• NCERT solutions for Class 9 Maths exercise 1.5 able us to develop our basic concepts regarding numbers and their characteristics.

• By solving the NCERT solution for Class 9 Maths chapter 1 exercise 1.5 exercises, it develops a strong foundation of Mathematical knowledge and of course more confidence in tackling new topics in our higher classes.

• Exercise 1.5 Class 9 Maths, will help us in learning how to perform operations on real numbers and this may help us in higher classes.

Key Features of class 9 maths chapter 1 exercise 1.5

Application of Concepts: This ex 1.5 class 9 often requires students to apply the concepts learned in the chapter to solve real-world problems.
Challenging Problems: Some class 9 maths ex 1.5 questions may be more challenging, requiring students to think critically and use problem-solving skills.
Practice for Competitive Exams: The questions in exercise 1.5 class 9 maths may serve as good practice for students preparing for competitive exams or Olympiads.
Enhances Problem-Solving Skills: Solving class 9 ex 1.5 problems enhances students' problem-solving and analytical skills.
Step-by-Step Solutions: Class 9 Maths Chapter 1 exercise 1.5 provides step-by-step solutions for Exercise 1.5 in the textbook or through supplementary materials, helping students understand the problem-solving process.
Self-assessment: After solving the questions in this exercise, students can assess their understanding of the chapter's concepts.
Preparation for Board Exams: 9th class maths exercise 1.5 answers are aligned with the CBSE board exam pattern, making it essential for board exam preparation.

Overall, Exercise 1.5 in Class 9 Maths serves as a crucial component of the curriculum, helping students practice and reinforce the mathematical concepts learned in the chapter.

Also see-

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. According to NCERT solutions for Class 9 Maths, 1 exercise 1.5 The associative property is applicable to ______

The associative property is applicable to Addition and Multiplication

Option (c) Addition and Multiplication

2. State true or false: The product of rational and irrational numbers is always an irrational number

Yes, the given statement is true. The product of a rational and an irrational number is always an irrational number.

3. Which property do the given statements hold? 2+3=3+2

2+3=3+2 holds the commutative property of addition.

4. Give one example for the commutative property of multiplication.

The example for the commutative property of multiplication is 5×2=2×5

5. Which of the two operations satisfy the condition of the associative property?

The two operations which satisfy the condition of the associative property are

Addition
Multiplication.

6. According to NCERT solutions for Class 9 Maths chapter 1 exercise 1.5, state the commutative property?

Commutative law states that when two numbers are added or multiplied together, a change in their locations has no effect on the outcome, according to NCERT solutions for Class 9 Maths chapter 1 exercise 1.5.

7. What is the total number of questions in the NCERT solutions for Class 9 Maths chapter 1 exercise 1.5 and What kind of questions are asked in NCERT solutions for Class 9 Maths chapter 1 exercise 1.5?

NCERT solutions for Class 9 Maths chapter 1 exercise 1.5 consists of 5 questions which are based on the classification of numbers into rational and irrational numbers by using certain operations and the representation of a given real number on the number line.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

AMU Class 1 Admission 2025: Application Process, Eligibility & Key Dates

Dec 30, 2024

Jamia Millia Islamia School Admission 2025: Application Process, Eligibility & Dates

Dec 30, 2024

SoSE Delhi School Admission 2025: All You Need to Know About Eligibility, Dates & Process

Dec 30, 2024

DBSE Result 2025, Check Delhi Board 10th, 12th Result

Dec 30, 2024

NMMS Chhattisgarh Result 2024-25: Check Merit List, Cut Off Marks

Dec 28, 2024

CBSE Scholarship 2024-25: Check CBSE Scholarships for Class 10, 12

Dec 27, 2024

HOS 12th Date Sheet 2025 - Haryana Open School Class 12 Exam Schedule

Dec 27, 2024

AMU School Admission 2025 - Know Application Process, Eligibility & Important Dates

Dec 27, 2024

Upcoming School Exams

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Admit Card

Result

National Institute of Open Schooling 10th examination

Late Fee Application Date:21 December,2024 - 31 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Late Fee Application Date:21 December,2024 - 31 December,2024

Application Process

Exam Pattern

Admit Card

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Exam Pattern

Answer Key

Result

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is