NCERT Solutions for Class 7 Maths Chapter 6 Number Play
Number Play shows that math isn’t just about answers, it’s about the joy of exploring patterns. Class 7 Maths NCERT Chapter 6 is an integral part of the syllabus and carries significant weightage in the final exam. This chapter briefly introduces patterns, the relationship between numbers, parity, magic square, Virahāṅka–Fibonacci Numbers, to students. The aim of these NCERT solutions for Class 7 Maths is to clear students' doubts about this chapter and provide them with important study material to learn all the necessary concepts. Many teachers recommend NCERT Solutions because they closely match the exam pattern.
This Story also Contains
- NCERT Solutions for Class 7 Maths Chapter 6 Number Play: Download Free PDF
- NCERT Solutions for Class 7 Maths Chapter 6 Number Play: Exercise
- Number Play Class 7 NCERT Solutions: Topics
- NCERT Solutions for Class 7 Maths Chapter 6 Number Play: Notes
- Class 7 Maths Chapter 6 Number Play Solutions: Extra Question
- Why are Class 7 Maths Chapter 6 Number Play Question Answers Important?
- NCERT Solutions for Class 7 Maths Chapter Wise
- NCERT Books and NCERT Syllabus

The Number Play chapter adds a new dimension of excitement to studying and learning mathematics. Curious minds will find patterns, tricks, and functions combined in this chapter. These NCERT solutions for Class 7 are created by experienced Careers360 teachers in a student-friendly manner, allowing students to understand all the Number Play Class 7 NCERT Solutions in a step-by-step approach and solve similar questions independently in the future. For full syllabus coverage and solved exercises, as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 7 Maths Chapter 6 Number Play: Download Free PDF
Careers360 brings you NCERT Class 7 Maths Chapter 6 Number Play solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 7 Maths Chapter 6 Number Play: Exercise
Here are the NCERT Class 7 Maths Chapter 6 Number Play question answers with clear and detailed solutions.
|
Number Play Class 7 Question Answers |
Question 1: Arrange the stick figure cutouts given at the end of the book, or draw a height arrangement such that the sequence reads:
(a) 0, 1, 1, 2, 4, 1, 5
(b) 0, 0, 0, 0, 0, 0, 0
(c) 0, 1, 2, 3, 4, 5, 6
(d) 0, 1, 0, 1, 0, 1, 0
(e) 0, 1, 1, 1, 1, 1, 1
(f) 0, 0, 0, 3, 3, 3, 3
Solution:
(a)
0, 1, 1, 2, 4, 1, 5
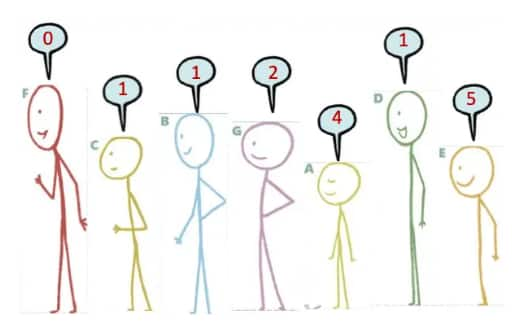
(b)
0, 0, 0, 0, 0, 0, 0
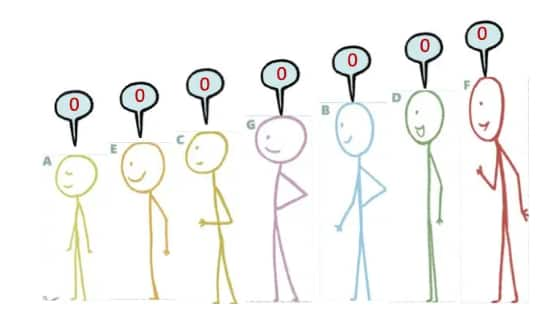
(c)
0, 1, 2, 3, 4, 5, 6
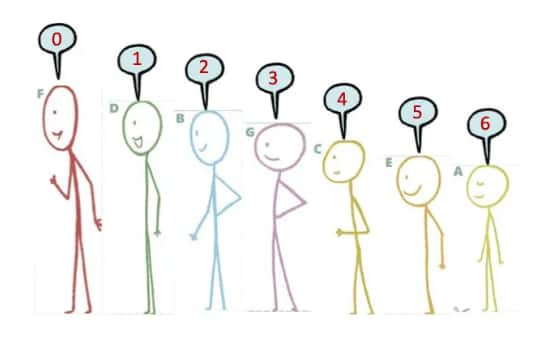
(d)
0, 1, 0, 1, 0, 1, 0
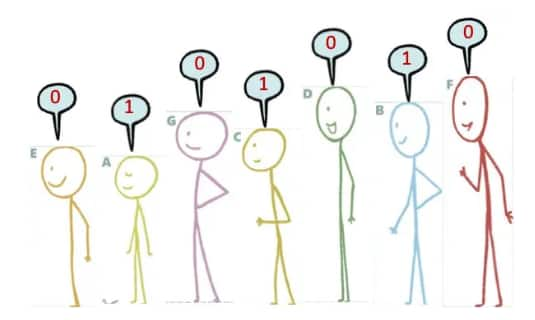
(e)
0, 1, 1, 1, 1, 1, 1

(f)
0, 0, 0, 3, 3, 3, 3
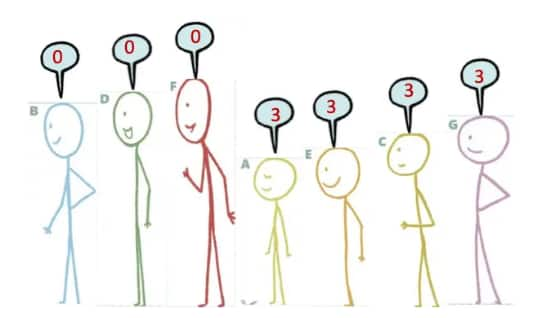
Question 2: For each of the statements given below, think and identify if it is Always True, Only Sometimes True, or Never True. Share your reasoning.
(a) If a person says ‘0’, then they are the tallest in the group.
(b) If a person is the tallest, then their number is ‘0’.
(c) The first person’s number is ‘0’.
(d) If a person is not first or last in line (i.e., if they are standing somewhere in between), then they cannot say ‘0’.
(e) The person who calls out the largest number is the shortest.
(f) What is the largest number possible in a group of 8 people?
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Number Play Class 7 Question Answers Page number: 131 Number of Questions: 3 |
Question 1: Using your understanding of the pictorial representation of odd and even numbers, find out the parity of the following sums:
(a) Sum of 2 even numbers and 2 odd numbers (e.g., even + even + odd + odd)
(b) Sum of 2 odd numbers and 3 even numbers
(c) Sum of 5 even numbers (d) Sum of 8 odd numbers
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 2: Lakpa has an odd number of ₹1 coins, an odd number of ₹5 coins and an even number of ₹10 coins in his piggy bank. He calculated the total and got ₹205. Did he make a mistake? If he did, explain why. If he didn’t, how many coins of each type could he have?
Solution:
Lakpa has an odd number of ₹1 coins.
1 × odd = odd
He has an odd number of ₹5 coins.
5 × odd = odd
He has an even number of ₹10 coins.
10 × even = Even
We know, Odd + Odd = Even
Then, Even + Even = Even
But 205 is not an even number.
So, it can’t be possible.
Question 3: We know that:
(a) even + even = even
(b) odd + odd = even
(c) even + odd = odd
Similarly, find out the parity for the scenarios below:
(d) even – even = ___________________
(e) odd – odd = ___________________
(f) even – odd = ___________________
(g) odd – even = ___________________
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Number Play Class 7 Question Answers Page number: 136 Number of Questions: 5 |
Question 1: How many different magic squares can be made using the numbers 1 – 9?
Solution:
A magic square means all rows, columns, and diagonals sum to the same number.
Here, Magic Sum $=\frac{1+2+3+4+5+6+7+8+9}{3}=\frac{45}{3}=15$
There can be one magic square using the numbers 1 to 9.
|
|
|
|
|
|
|
|
|
|
|
|
Question 2: Create a magic square using the numbers 2 – 10. What strategy would you use for this? Compare it with the magic squares made using 1 – 9.
Solution:
$
\text { Here, Magic Sum }=\frac{2+3+4+5+6+7+8+9+10}{3}=\frac{54}{3}=18
$
There can be a magic square possible with numbers $2-10$.
|
|
|
|
|
|
|
|
|
|
|
|
Both structures are the same. But the magic sum is different.
Question 3: Take a magic square, and
(a) Increase each number by 1
(b) Double each number in each case, is the resulting grid also a magic square? How do the magic sums change in each case?
Solution:
(a)
We can take the example of Questions 1 and 2 for this question.
Magic Square of numbers from 1 to 9.
|
|
|
|
|
|
|
|
|
|
|
|
After adding 1 to each number, we will get the following magic square.
|
|
|
|
|
|
|
|
|
|
|
|
(b)
If we double each number, the magic sum will also be doubled.
The magic sum increases from 15 to 30.
New magic square:
|
|
|
|
|
|
|
|
|
|
|
|
Question 4: What other operations can be performed on a magic square to yield another magic square?
Solution:
Here are some operations that can be performed on a magic square to yield another magic square.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 5: Discuss ways of creating a magic square using any set of 9 consecutive numbers
(like 2 – 10, 3 – 11, 9 – 17, etc.).
Solution:
Magic square using 2-10
Here, the magic sum = 18
|
|
|
|
|
|
|
|
|
|
|
|
We can add one with each number to get a magic square of 3-11.
Here, magic sum = 21
|
|
|
|
|
|
|
|
|
|
|
|
We have to add 6 to each number to get a magic square of 9-17.
Here, magic sum = 39
|
|
|
|
|
|
|
|
|
|
|
|
|
Number Play Class 7 Question Answers Page number: 137 Number of Questions: 5 |
Question 1: Using this generalised form, find a magic square if the centre number is 25.
Solution:
Generalised form of a magic square:
|
|
|
|
|
|
|
|
|
|
|
|
So, if the centre number is 25, the magic square will be:
|
|
|
|
|
|
|
|
|
|
|
|
Question 2: What is the expression obtained by adding the 3 terms of any row, column or diagonal?
Solution:
Let's take the last magic square as an example.
|
|
|
|
|
|
|
|
|
|
|
|
1st row sum = 28 + 21 + 26 = 75
1st column sum = 28 + 23 + 24 = 75
Diagonal sum = 28 + 25 + 22 = 75
As we can see, it gives the magic sum when we add three terms of any row, column, or diagonal.
Question 3: Write the result obtained by—
(a) Adding 1 to every term in the generalised form.
(b) Doubling every term in the generalised form
Solution:
Generalised form of a magic square:
|
|
|
|
|
|
|
|
|
|
|
|
(a)
Adding 1 to every term in the generalised form:
|
|
|
|
|
|
|
|
|
|
|
|
We can see that the magic square still holds, as the new magic sum = 3K + 3
(b)
Doubling every term in the generalised form
|
|
|
|
|
|
|
|
|
|
|
|
We can see that the magic square still holds, as the new magic sum = 2K
Question 4: Create a magic square whose magic sum is 60.
Solution:
In the magic square of 1 to 9, the magic sum is 15.
|
|
|
|
|
|
|
|
|
|
|
|
So, to get a magic sum of 60, we need to multiply every digit of the magic square from 1 to 9 by 4 as
15 × 4 = 60
|
|
|
|
|
|
|
|
|
|
|
|
Here,
Row sums:
32 + 4 + 24 = 60
12 + 20 + 28 = 60
16 + 36 + 8 = 60
Column sums:
32 + 12 + 16 = 60
4 + 20 + 36 = 60
24 + 28 + 8 = 60
Diagonals:
32 + 20 + 8 = 60
24 + 20 + 16 = 60
Question 5: Is it possible to get a magic square by filling nine non-consecutive numbers?
Solution:
Yes, a magic square can be formed with 9 non-consecutive numbers if they still follow an arithmetic progression.
For example, all even numbers, or numbers with a common difference.
Here is a magic square with 3,6,9,12,15,18,21,24,27.
As you can see, the common difference between all the numbers is 3.
|
|
|
|
|
|
|
|
|
|
|
|
Here, the magic sum = 45
But it is impossible to create a magic square if the 9 numbers are just random, non-consecutive numbers with no pattern.
|
Number Play Class 7 Question Answers Page number: 143-144 Number of Questions: 11 |
Question 1: A light bulb is ON. Dorjee toggles its switch 77 times. Will the bulb be on or off? Why?
Solution:
Initially, the light bulb is on.
So, if Dorjee toggles 1 time, then it will be off.
Subsequently, if he toggles two times, the bulb will be on again.
As we can see, after an odd number of times, the bulb is off, and after an even number of times, the bulb is on.
77 is an odd number.
So, the bulb will be off after Dorjee toggles its switch 77 times.
Question 2: Liswini has a large old encyclopedia. When she opened it, several loose pages fell out of it. She counted 50 sheets in total, each printed on both sides. Can the sum of the page numbers of the loose sheets be 6000? Why or why not?
Solution:
Total sheets = 50
Each sheet has one even and one odd page number.
Thus, the total of 50 sheets consists of 50 even numbers and 50 odd numbers.
We know that the sum of an even number of odd numbers is “Even”.
And the Sum of an even number of even numbers is also “Even”.
Thus, the total sum is even + even = even.=
Since 6000 is an even number, it is possible for the sum of the page numbers of the loose sheets to be 6000.
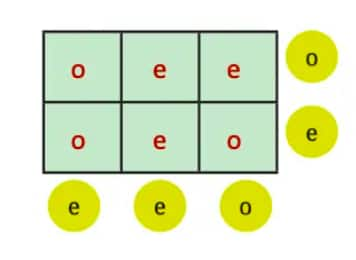
Question 3: Here is a 2 × 3 grid. For each row and column, the parity of the sum is written in the circle; ‘e’ for even and ‘o’ for odd. Fill the 6 boxes with 3 odd numbers (‘o’) and 3 even numbers (‘e’) to satisfy the parity of the row and column sums.
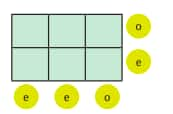
Solution:
Question 4: Make a 3 × 3 magic square with 0 as the magic sum. All numbers can not be zero. Use negative numbers, as needed.
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
Question 5: Fill in the following blanks with ‘odd’ or ‘even’:
(a) Sum of an odd number of even numbers is ______
(b) Sum of an even number of odd numbers is ______
(c) Sum of an even number of even numbers is ______
(d) Sum of an odd number of odd numbers is ______
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 6: What is the parity of the sum of the numbers from 1 to 100?
Solution:
In numbers from 1 to 100, there are 50 odd numbers and 50 even numbers.
We know that the sum of an even number of odd numbers is “Even”.
And the Sum of an even number of even numbers is also “Even”.
So, Even + Even = Even.
Hence, the parity of the sum of numbers from 1 to 100 is even.
Question 7: Two consecutive numbers in the Virahāṅka sequence are 987 and 1597. What are the next 2 numbers in the sequence? What are the previous 2 numbers in the sequence?
Solution:
A Virahāṅka sequence is a sequence where each number is the sum of the two preceding numbers.
So, the next number in the sequence = 987 + 1597 = 2584
After that, the next number in the sequence = 1597 + 2584 = 4181
Let the previous number of 987 in the sequence be x.
So, 1597 = x + 987
⇒ x = 1597 - 987 = 610
Let the previous number of 610 in the sequence be y.
So, 987 = y + 610
⇒ y = 987 - 610 = 377
Thus, the total sequence is:
377, 610, 987, 1597, 2584, 4181
Question 8: Angaan wants to climb an 8-step staircase. His playful rule is that he can take either 1 step or 2 steps at a time. For example, one of his paths is 1, 2, 2, 1, 2. In how many different ways can he reach the top?
Solution:
This problem is a variation of the Fibonacci sequence, where:
At each step, Angaan can either take 1 step or 2 steps.
And the number of ways to reach step n is the sum of the ways to reach step n−1 and step n−2.
So, f(n) = f(n-1) + f(n-2)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hence, the number of different ways Angaan can reach the top of the 8-step staircase is 34.
Question 9: What is the parity of the 20th term of the Virahāṅka sequence?
Solution:
Virahāṅka sequence:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,…
We can see a pattern.
1 (odd), 2 (even), 3 (odd), 5 (odd), 8 (even), 13 (odd), 21 (odd), 34 (even), 55 (odd), 89 (odd),…
This pattern repeats every 3 terms.
So, after 6 × 3 = 18 terms, the pattern will again be odd, even, odd.
19th term = odd
20th term = even
21st term = odd
Hence, the parity of the 20th term of the Virahāṅka sequence is “even”.
Question 10: Identify the statements that are true.
(a) The expression 4m – 1 always gives odd numbers.
(b) All even numbers can be expressed as 6j – 4.
(c) Both expressions 2p + 1 and 2q – 1 describe all odd numbers.
(d) The expression 2f + 3 gives both even and odd numbers.
Solution:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
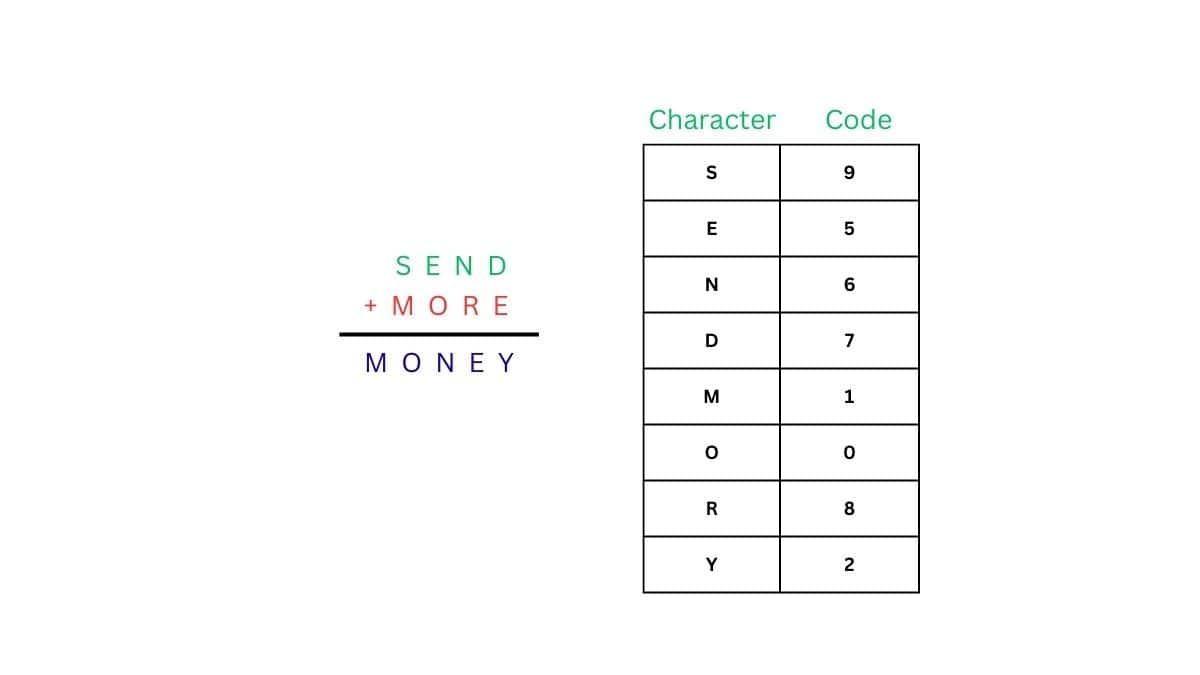
Question 11: Solve this cryptarithm:
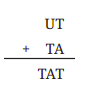
Solution:
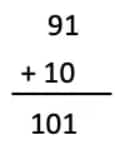
Where, U = 9, T = 1 and A = 0
Number Play Class 7 NCERT Solutions: Topics
Students will explore the following topics in NCERT Class 7 Maths Chapter 6 Number Play:
- Numbers Tell Us Things
- Picking Parity
- Some Explorations in Grids
- Nature’s Favourite Sequence: The Virahāṅka– Fibonacci Numbers!
- Digits in Disguise
NCERT Solutions for Class 7 Maths Chapter 6 Number Play: Notes
Careers360 has prepared these Class 7 Number Play Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Number Play NCERT solutions and solve them independently from next time.
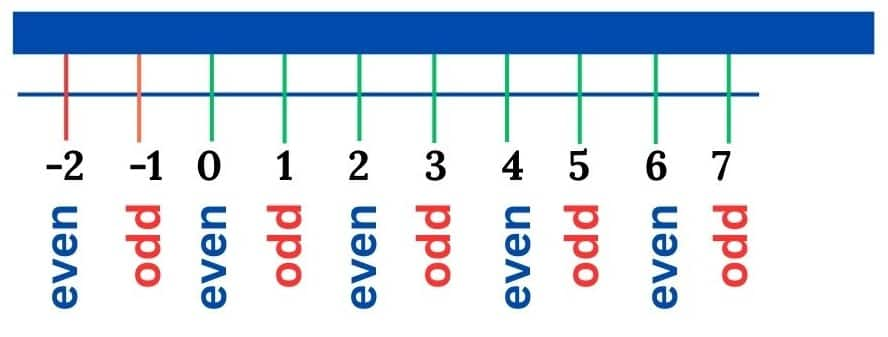
Parity
In mathematics, parity refers to whether an integer is even or odd.
-
An even number is divisible by 2 (remainder 0).
-
An odd number is not divisible by 2 (remainder 1).
So, parity tells us the “evenness” or “oddness” of an integer.
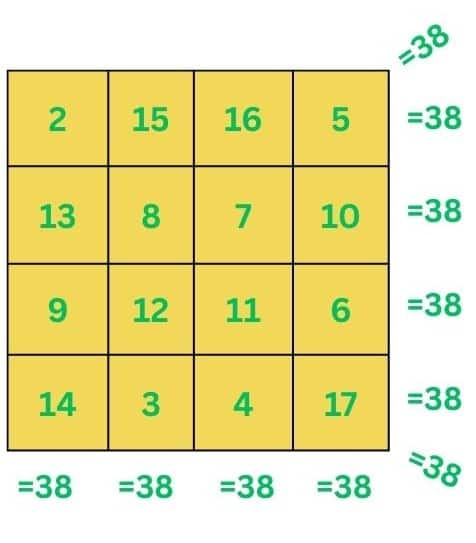
Magic Square in Mathematics
A Magic Square is a special square arrangement of numbers in which the sum of the numbers in each row, each column, and both diagonals is the same.
This common sum is called the magic constant or magic sum.
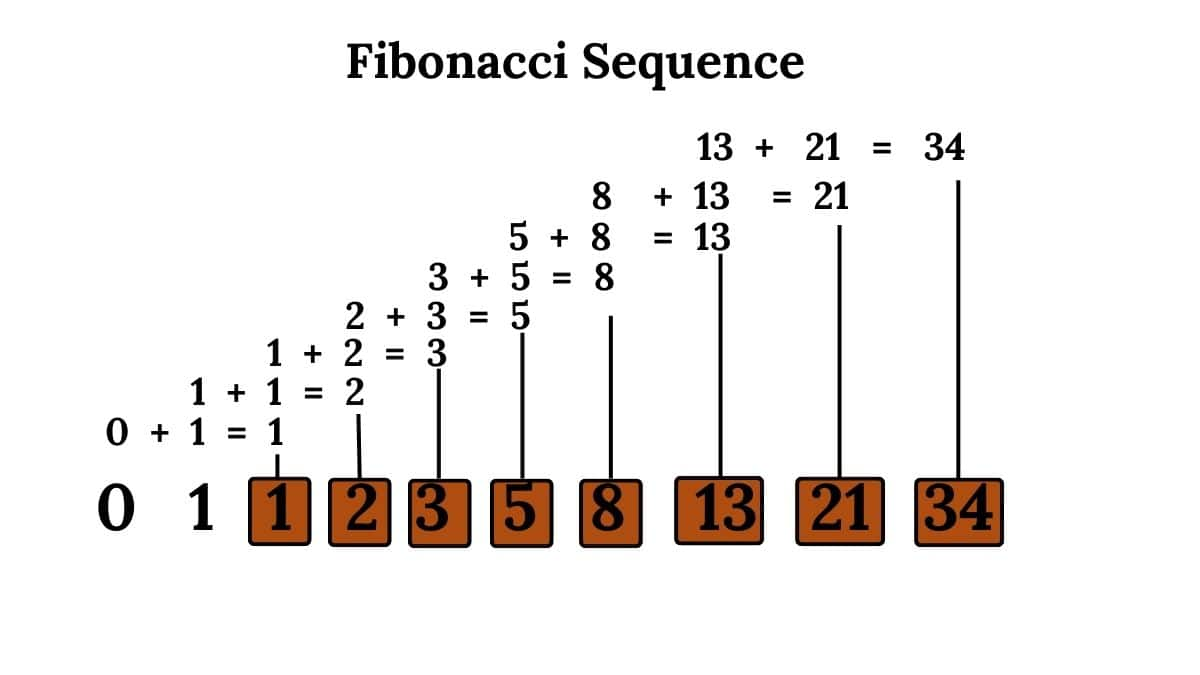
Fibonacci Numbers
The Fibonacci sequence is a series of numbers where each number is the sum of the two numbers before it.
$F_0=0, F_1=1, F_n=F_{n-1}+F_{n-2} \quad(n \geq 2)$
The Fibonacci numbers were first described by Virahāṅka in India for poetic meters. Fibonacci later introduced them to Europe with a different context.
Cryptarithm
A cryptarithm (also called an anagrammatic puzzle) is a mathematical puzzle in which each letter represents a single decimal digit.
Here are some rules that are followed in cryptarithm.
-
Different letters → different digits.
-
Same letter → same digit everywhere.
-
No number has a leading zero (so the leftmost letter of a multi-digit number ≠ 0).
-
The arithmetic (addition, subtraction, multiplication, etc.) must be correct once letters are replaced by digits.
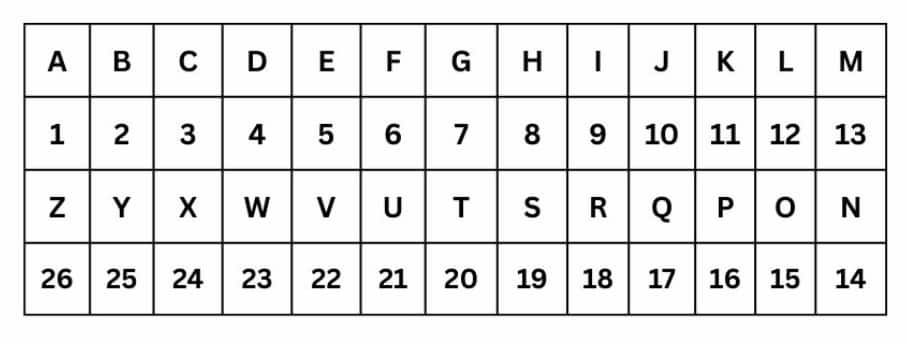
Place value of letters
Class 7 Maths Chapter 6 Number Play Solutions: Extra Question
Question:
The Fibonacci sequence is formed by adding the two previous numbers to get the next one: $0,1,1,2,3,5,8,13, \ldots$
Find the 10th term of the Fibonacci sequence.
Solution:
Let’s write the sequence step by step:
-
1st term = 0
-
2nd term = 1
-
3rd term = 0 + 1 = 1
-
4th term = 1 + 1 = 2
-
5th term = 1 + 2 = 3
-
6th term = 2 + 3 = 5
-
7th term = 3 + 5 = 8
-
8th term = 5 + 8 = 13
-
9th term = 8 + 13 = 21
-
10th term = 13 + 21 = 34
Hence, the correct answer is 34.
Why are Class 7 Maths Chapter 6 Number Play Question Answers Important?
The sixth chapter of class 6, titled Number Play, helps us see how numbers have patterns and special properties. It makes maths more fun by showing the hidden tricks and ideas behind numbers. These Class 7 Maths chapter 6 Number Play question answers help us understand these ideas better through simple problems and examples. Here are some more points on why these question answers are important.
- These solutions help us identify patterns in numbers and understand how they work together.
- Students learn about odd and even numbers, number grids, and special sequences such as the Fibonacci numbers.
- Practising Class 7 Maths chapter 6 Number Play question answers helps us in higher classes when you learn about sequences and patterns in detail.
NCERT Solutions for Class 7 Maths Chapter Wise
The links below allow students to access all the Maths Class 7 solutions from the NCERT book.
NCERT Books and NCERT Syllabus
Students can also check the NCERT Books and the NCERT Syllabus here:
Frequently Asked Questions (FAQs)
The topics discussed in the NCERT Solutions for Class 7 Maths Chapter 6 Number Play are:
- Numbers Tell Us Things
- Picking Parity
- Some Explorations in Grids
- Nature’s Favourite Sequence: The Virahāṅka– Fibonacci Numbers!
- Digits in Disguise
The chapter, Number Play, explores fun number patterns, magic squares, and even–odd sequences to build logical reasoning through puzzles and numeric games.
The chapter includes multiple “Figure It Out” activities and puzzles, such as height arrangements, magic squares, and sum and parity challenges, designed to strengthen conceptual understanding.
These Number Play Class 7 NCERT Solutions offer step-by-step explanations for every puzzle and pattern, helping students decode rules and improve problem-solving strategies.
A magic square is a 3×3 grid where all rows, columns, and diagonals sum to the same value. Students learn how to form them using consecutive numbers and how operations on grids change the constant sum.
Many educational platforms, such as Careers360, offer free downloadable PDFs of Class 7 Number Play Solutions. Students can find the free downloadable PDF in this article itself.
“Picking Parity” is about understanding even and odd numbers and how their properties change under addition, subtraction, and multiplication.
For example, even + even = even, while even + odd = odd.
The Virahāṅka–Fibonacci sequence is a famous pattern found in nature, where each number is the sum of the two before it (1, 1, 2, 3, 5, 8, 13...).
It appears in flowers, shells, and even art, showing how mathematics connects to nature.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
