CBSE Class 10: How Quadratic Equations Can Help You Make A Shot In Basketball

Understanding Quadratic Equations: The Basics

Before we delve into the world of basketball, let's revisit the basics of quadratic equations.
A quadratic equation is a second-order polynomial equation containing a single variable $x$.
It typically looks like this: $a x^2+b x+c=0$

Here, $x$ is the variable, and $a, b,$ and $c$ are constants. It is important to note that $a$ should not be equal to 0. The solutions to this equation are the values of $x$ that satisfy the equation and make it equal to zero. These solutions are known as the "roots" of the quadratic equation.

Methods to Solve Equations

Solving quadratic equations is like solving a puzzle. Sometimes, the equation can be factored easily, while at other times, you need a more sophisticated approach, such as completing the square or using the quadratic formula. Let's discuss these three techniques in detail.

Factoring Method

Factoring means expressing the quadratic equation as a product of two simpler expressions (binomials). Think of it as taking apart a Lego structure to see its smaller pieces.

Here's how it works:

Step 1: Start with the equation: $a x^2+b x+c=0$
Step 2: Identify $a, b$, and $c$.
Step 3: Find two numbers that multiply to $a \times c$ and add up to $b$.
Step 4: Split the middle term (bx) using those two numbers.
Step 5: Factor by grouping.
Step 6: Set each factor equal to zero to find $x$.

Let's see an example:

Equation: $x^2+5 x+6=0$

• ${a}=1, {~b}=5$, and ${c}=6$
• Numbers that multiply to ' $1 \times 6$ ' and add up to 5 are 2 and 3.
• Rewrite $5x$ as ' $2 {x}+3 x$ '.
• Factor: $(x+2)(x+3)=0$

Now, set each factor equal to zero:

$
\begin{aligned}
& x+2=0 \Rightarrow x=-2 \\
& x+3=0 \Rightarrow x=-3
\end{aligned}
$
So, the solutions are $x=-2$ and $x=-3$.

Completing the Square

This method transforms a quadratic equation into a perfect square form. It’s slightly longer but extremely useful when factoring doesn’t work.

Here's how it's done:

• Start with the quadratic equation in the form: $ax^2+bx+c=0$

• Divide the entire equation by $a$ to make the coefficient of $x^2$ equal to 1.

• Move the constant term ($\frac ca$) to the other side of the equation.

• Add and subtract the square of half of the coefficient of the $x$ term $\frac{b}{2 a}$.

The equation will then be in the form: $\left(x+\frac{b}{2 a}\right)^2=d$

Solve for $x$ to find the solutions.

Let's go through an example:

Equation: $x^2-6 x+8=0$

• Divide by $a$: $x^2-6 x+8=0$
• Move constant term: $\mathrm{x}^2-6 \mathrm{x}=-8$
• Add and subtract $(-\frac62 \times 1)^2= 9$

$
\begin{aligned}
& x^2-6 x+9=-8+9 \\
&\Rightarrow(x-3)^2=1
\end{aligned}
$

Now, take the square root of both sides:

$
\begin{aligned}
& x-3=\sqrt{ 1} \\
& \Rightarrow x-3= \pm 1
\end{aligned}
$
Solutions: $x=3 \pm 1$ that is $x=4$ and $x=2$

Quadratic Formula

When the equation isn’t easily factorable, the Quadratic Formula always works, as it is an effective method for students.

The formula goes as follows:
$x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$
Where:
$a=$ coefficient of $x^2$
$b=$ coefficient of $x$
$c=$ constant term
$\sqrt{b^2-4 a c}$ is called the discriminant

In this formula, $a, b,$ and $c$ are the coefficients from the original quadratic equation. The "±" symbol represents the two possible solutions, and the square root calculates the discriminant, which gives us insights into the nature of the roots.

In summary:

• Use Factoring for simple, clean quadratics.

• Use Completing the Square to understand structure and symmetry.

• Use the Quadratic Formula when nothing else works, as it is universal.

Also, read,
Smart Shopping CBSE Class 8: Comparing Quantities For Better Deals

Quadratic Equation Solver

Students can use the following link to solve and find the roots of quadratic equations in the form $ax^2+bx+c=0$. Values up to 12 can be checked there. Students can also plot the graph of the quadratic function and examine it at up to four different points. Additionally, the calculator displays key properties such as the discriminant, vertex coordinates, and the sum and product of roots, helping you understand how each coefficient affects the shape and position of the parabola.

Click on this link to use the Quadratic Equation Solver

For example:
Graph of $3x^2+4x+1=0$

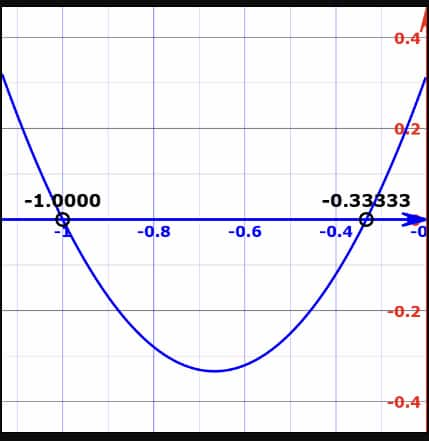
Roots are: $-1$ and $-0.33333$

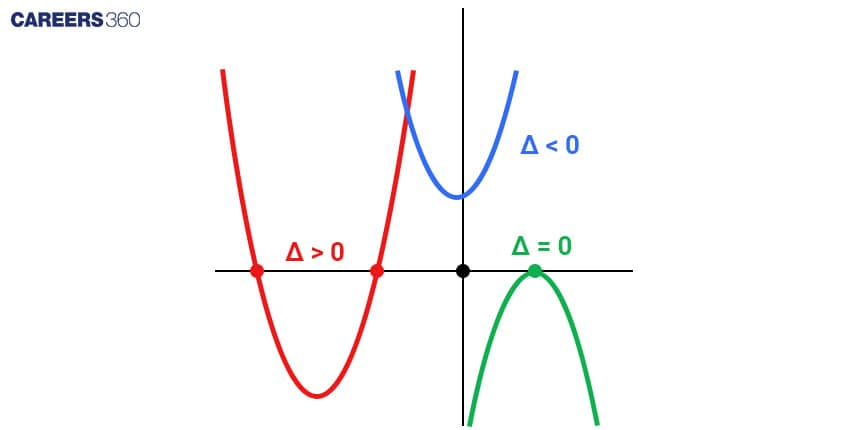
Discriminant and Root Classification

The discriminant (Δ) of a quadratic equation plays a crucial role in categorising its roots. The formula to calculate the discriminant is: Δ = $b^2-4 a c$

Based on the value of Δ, we can determine the nature of the roots:

• If Δ > 0, the equation has two distinct real roots.

• If Δ = 0, the equation has a single real root (a repeated root).

• If Δ < 0, the equation has two complex conjugate roots.

Understanding the discriminant helps us predict the behaviour of the equation without actually solving it.

Quadratic Equation Graphs

Graphs are powerful visual representations that provide insights into the behaviour of quadratic equations. By analysing the shape and key points of these graphs, we can understand how different coefficients and constants in quadratic equations affect their curves.
Let's explore the graphs of quadratic equations in various cases.

Case 1: [When $a$ is Positive]
When $a$ is positive, the graph of the quadratic equation opens upwards. This means the parabola has a minimum point. The larger the value of $a$, the narrower the parabola.

Example: $y=x^2$

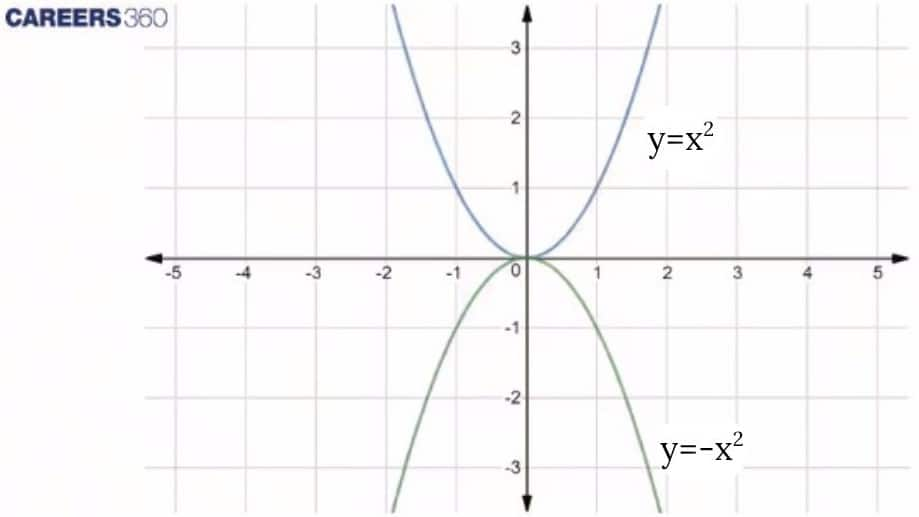
Case 2: [When $a$ is Negative]
When $a$ is negative, the graph of the quadratic equation opens downwards. The parabola has a maximum point. Again, the smaller the value of $a$, the wider the parabola.

Example: $y=-x^2$

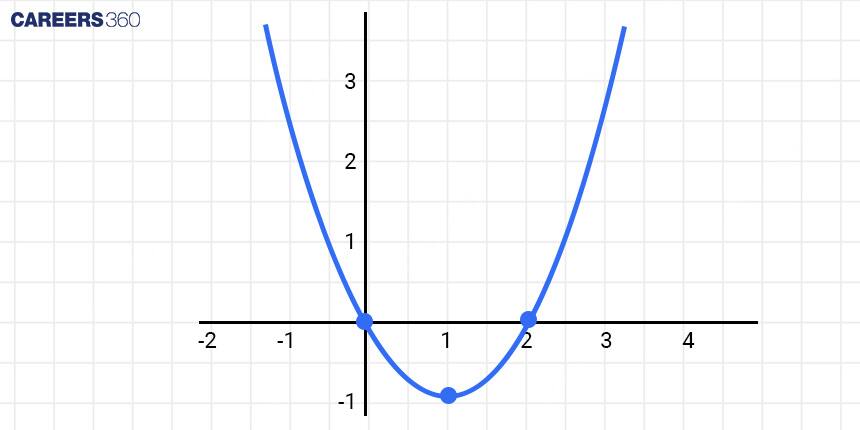
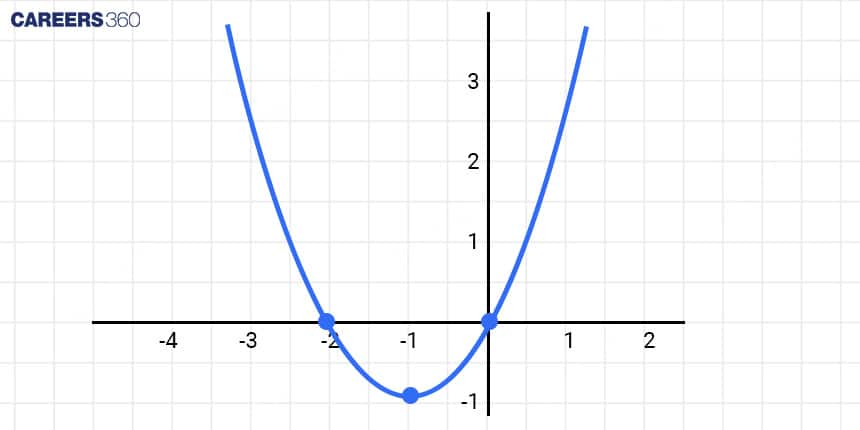
Case 3: [When$b$ is Positive or Negative]
The coefficient $b$ determines the horizontal shift of the parabola. If $b$ is positive, the parabola shifts to the left, and if $b$ is negative, it shifts to the right.

Examples:

• Positive $b$: $y=x^2-2 x$

• Negative $b$: $y=x^2+2 x$

Case 4: [Discriminant and Nature of Roots]
The discriminant (Δ) of a quadratic equation affects the number and nature of its roots. We can visualise this on the graph.

Δ > 0: Two real and distinct roots. The parabola intersects the x-axis at two points.

Δ = 0: One real repeated root. The parabola touches the x-axis at one point.

Δ < 0: Two complex conjugate roots. The parabola does not intersect the x-axis.

From Equations to Basketball: The Trajectory of a Shot

Now, let's transition from mathematics to the basketball court. When a basketball player takes a shot, the ball's path follows a curved trajectory. This trajectory is a result of the shot's initial velocity and the force of gravity pulling the ball downwards. This curving path is aptly described by quadratic equations.

Mathematics enables us to break down the elements of a basketball shot.

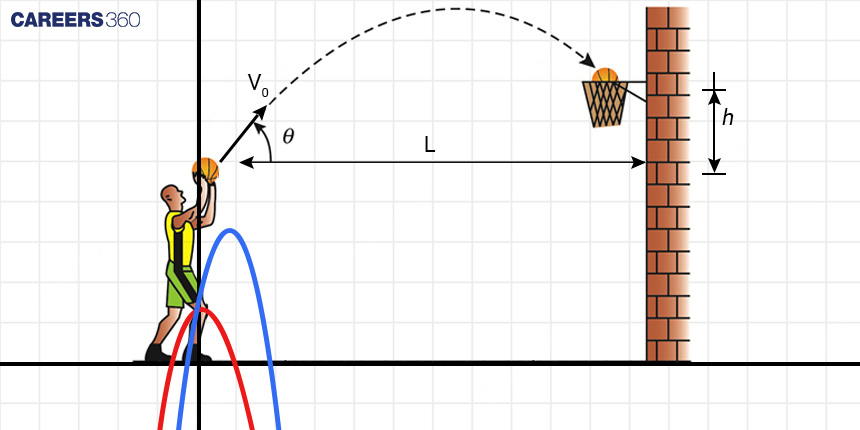
General Vertical Motion (with downward parabola)

Since the parabola opens downward, $a<0$. The vertical position $y$ of a ball over time $t$ can be written as:
$y=-\frac{1}{2} g t^2+v_0 \sin \theta t+h_0$

where:
$g=$ acceleration due to gravity
$v_0=$ initial velocity
$\theta=$ angle of projection
$h_0=$ initial height

Horizontal Motion
$x=v_0 \cos \theta t$

Trajectory Equation (eliminating t)
$y=x \tan \theta-\frac{g x^2}{2\left(v_0 \cos \theta\right)^2}+h_0$

Other form (if using feet and $g=32\ \mathrm{ft} / \mathrm{s}^2$)
$y=-16 t^2+v_0 \sin \theta t+h_0$

Must, Check,
Why You Should Give Mock Tests Even For Banking Exams?

The Quest for the Perfect Shot

A basketball player's ultimate goal is to nail the perfect shot – a shot that sails through the hoop with finesse. Achieving this requires understanding the interplay between the initial velocity $v$ and the angle of release. Quadratic equations hold the key to determining the parabolic arc that the ball will follow.

Different angles and velocities lead to various trajectories. By tinkering with these variables, players can fine-tune their shots. Quadratic equations help them comprehend the mechanics behind their shots and make informed decisions to enhance their accuracy.

Consider a basketball player who is aiming for a hoop placed at a height of 15 feet. The player of height 5 feet wants to shoot the ball at an angle of 45 degrees and an initial velocity of 50 feet per second. How far from the hoop should the player stand to make the shot?

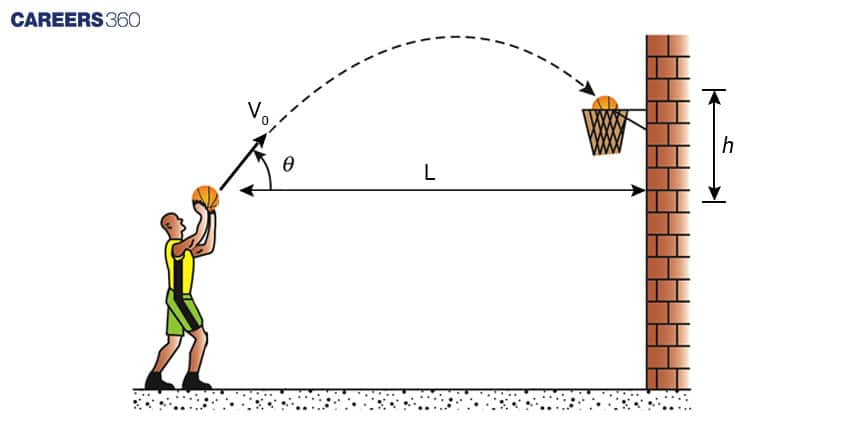
let's break down the key components of the problem:

• Initial angle of release $(θ)$: 45 degrees

• Initial velocity $(v_0)$: 50 feet per second

• Height of the hoop $(h)$: 15 feet - 5 feet = 10 feet (above the person)

• Acceleration due to gravity (g): 32 feet/ s²
  (negative since it's acting downward)

Quadratic equation for basketball written as

$y=-16 t^2+v_0 \sin \theta t+h_0$

After time t, the ball will reach the basket height:

$\begin{aligned} & -16 t^2+\frac{50}{\sqrt{2}} t-10=0 \\ & ⇒-16 t^2+35.36 t-10=0\end{aligned}$

Using the formula: $t=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$

Here: $a=-16, b=35.36, c=-10$
$t=\frac{-35.36 \pm \sqrt{(35.36)^2-4(-16)(-10)}}{2(-16)}$
$⇒t=\frac{-35.36 \pm \sqrt{1250.4-640}}{-32}$
$⇒t=\frac{-35.36 \pm \sqrt{610.4}}{-32}$
$⇒t=\frac{-35.36 \pm 24.71}{-32}$
Only positive time is meaningful:
So, $t=1.87$ seconds

Now, Horizontal distance, $x=v_0 \cos \theta t=50 \cos 45^{\circ}(1.87)=35.36 \times 1.87 \approx 65.85 \mathrm{ft}$

So, the basketball player should stand approximately 65.85 feet from the hoop to make a successful shot with an angle of 45 degrees and an initial velocity of 50 feet per second.

Understanding quadratic equations empowers players to adapt to different court positions, distances, and angles. Armed with this knowledge, players can adjust their shots dynamically, improving their overall accuracy and consistency.

Also, read,

• NCERT Books Class 10 Maths
• NCERT Syllabus Class 10 Maths
• NCERT Notes Class 10 Maths
• NCERT solutions for Class 10 Maths