NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2

NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 - Quadrilaterals

Vishal kumarUpdated on 22 May 2025, 03:14 PM IST

In the last exercise, the concept of quadrilaterals and their types and properties was explained. In this exercise, the concept of the midpoint theorem is used to solve the questions. The midpoint theorem is also called the midsegment theorem. According to this theorem, the line connecting the midpoint of the two sides of the triangle will be parallel to the third side and half its length.
The figure below shows a triangle ABC, and the line EF passes through the midpoints of the sides AB and AC. Since it divides the sides into two, AE = EB and AB = 2AE

NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 - Quadrilaterals

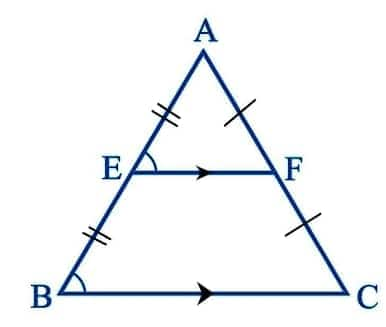
The two theorems that are present in the NCERT solutions for Class 9 Maths chapter 8 exercise 8.2 are:

The line segment joining the midpoints of the two sides of a triangle is parallel to the third side of the triangle (also known as the base of the triangle, generally).
The line segment that is drawn through the midpoint of one side of a triangle, and moves parallel to the third side of the triangle (base) bisects the other side of the triangle into two halves.

This chapter takes you into the study of quadrilaterals, four-sided shapes. 9th class maths exercise 8.2 answers provide practical problems and solutions to help you understand their properties and types. Access these free PDF solutions to improve your understanding, prepare for exams, and strengthen your math skills. The NCERT Solutions for Class 9 Maths Exercise 8.2 deal with concepts that are mostly related to triangles rather than quadrilaterals. The NCERT Books help students to access all the study material according to their requirements.

NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.2

Access Quadrilaterals Class 9 Chapter 8 Exercise: 8.2

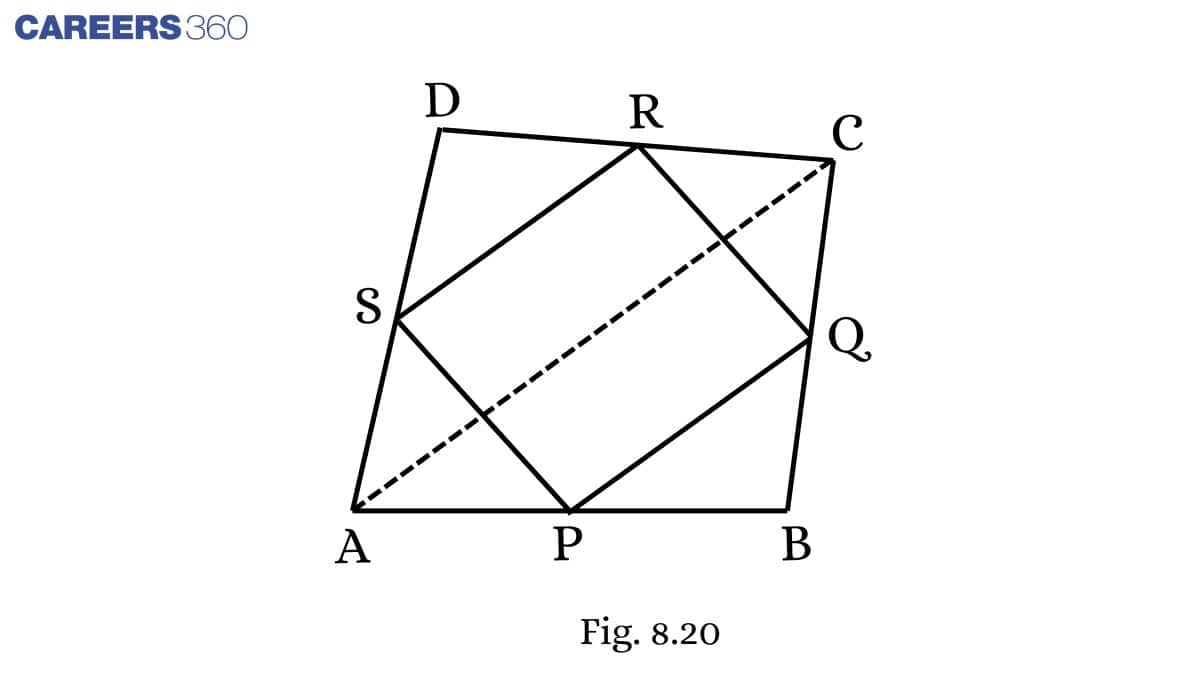
Q1 (i) ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.20 ). AC is a diagonal. Show that : SR∥AC and SR=12AC

Solution:

Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29 ). AC is a diagonal.

To prove:

SR∥AC and SR=12AC

Proof: In △ ACD,

S is the midpoint of DA. (Given)

R is the midpoint of DC. (Given)

By the midpoint theorem,

SR∥AC and SR=12AC

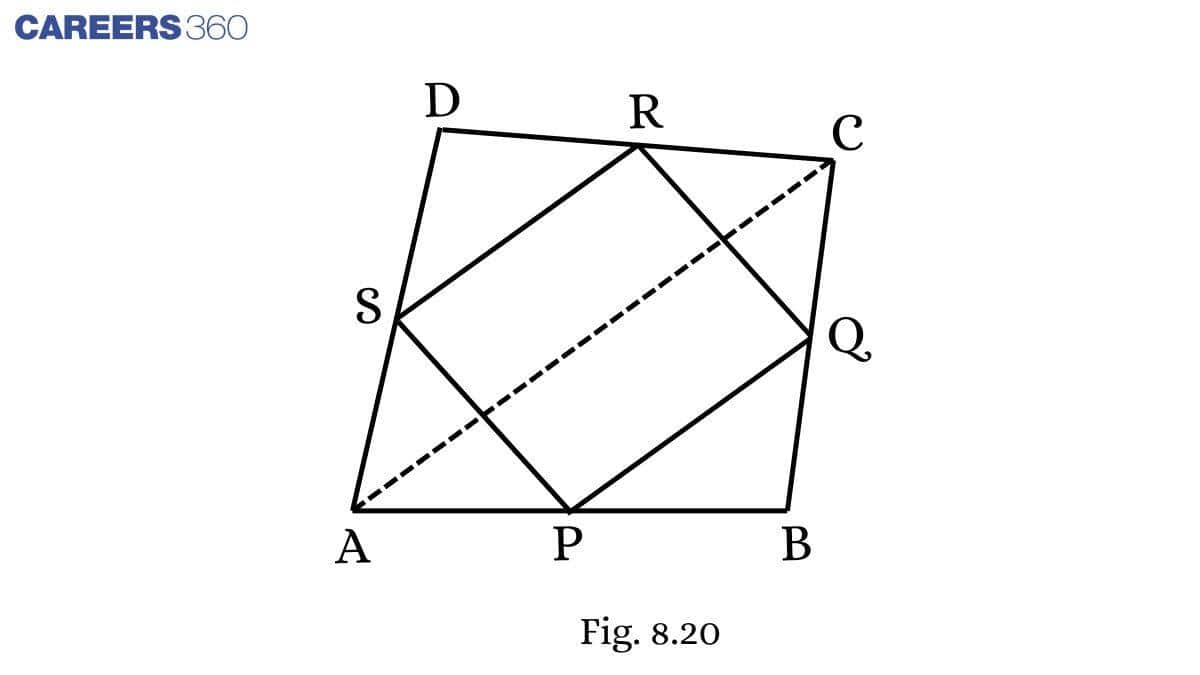
Q1 (ii) ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.20 ). AC is a diagonal. Show that : PQ=SR

Solution:

Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29 ). AC is a diagonal.

To prove : PQ=SR

Proof: In △ ACD,

S is the midpoint of DA. (Given)

R is the midpoint of DC. (Given)

By the mid-point theorem,

SR∥AC and SR=12AC ...........(1)

In △ ABC,

P is the midpoint of AB. (Given)

Q is the midpoint of BC. (Given)

By the mid-point theorem,

PQ∥AC and PQ=12AC ..............(2)

From 1 and 2, we get

PQ∥SR and PQ=SR=12AC

Thus, PQ=SR

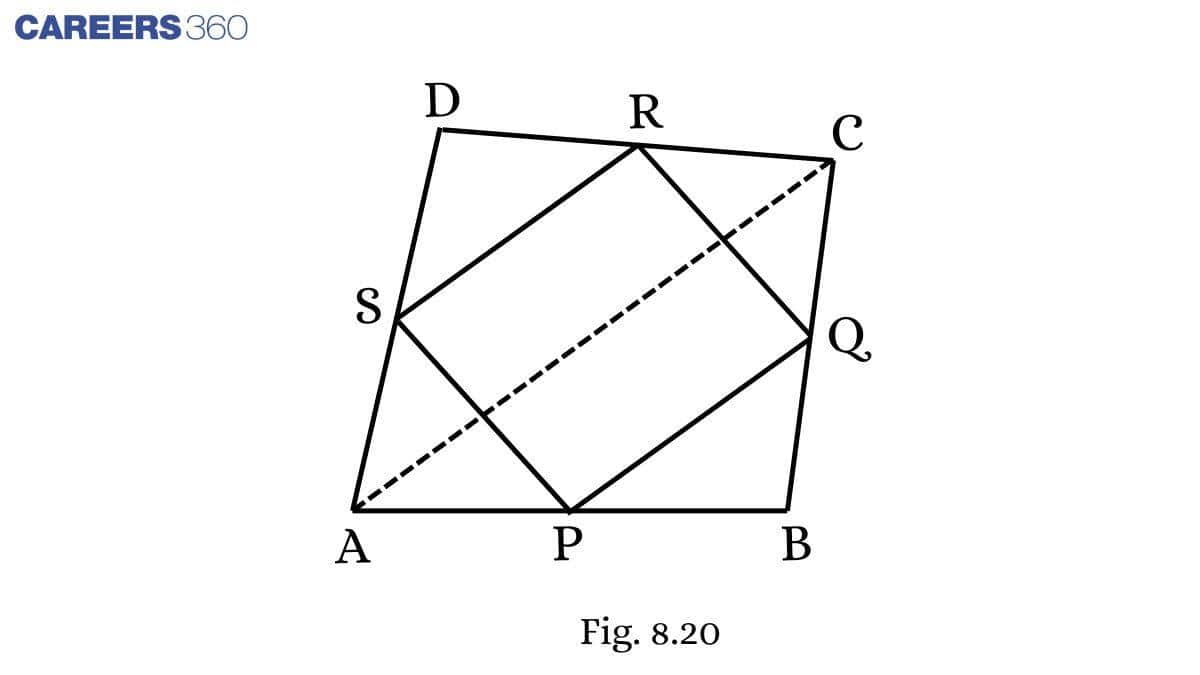
Q1 (iii) ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.20 ). AC is a diagonal. Show that : PQRS is a parallelogram.

Solution:

Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29 ). AC is a diagonal.

To prove: PQRS is a parallelogram.

Proof: In PQRS,

Since,

PQ∥SR and PQ=SR .

So, PQRS is a parallelogram.

Q2 ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

Solution:

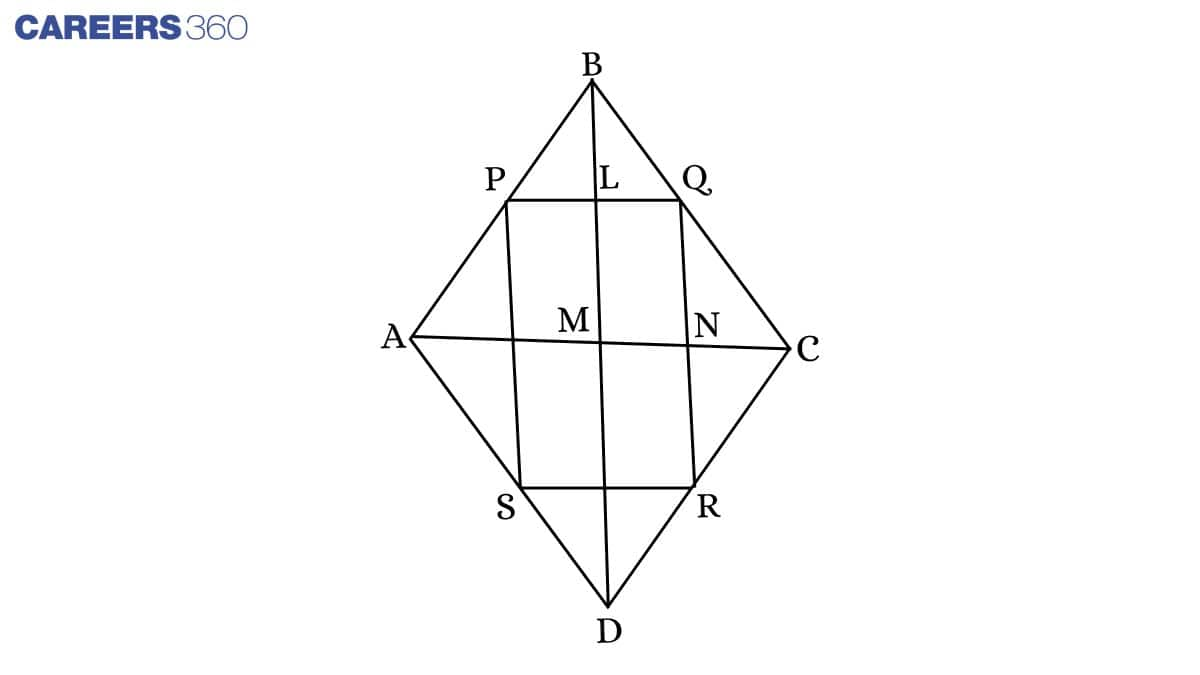
Given: ABCD is a rhombus in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC, BD are diagonals.

To prove: the quadrilateral PQRS is a rectangle.

Proof: In △ ACD,

S is the midpoint of DA. (Given)

R is the midpoint of DC. (Given)

By the midpoint theorem,

SR∥AC and SR=12AC ........(1)

In △ ABC,

P is the midpoint of AB. (Given)

Q is the midpoint of BC. (Given)

By the mid-point theorem,

PQ∥AC and PQ=12AC ...........(2)

From (1) and (2), we get

PQ∥SR and PQ=SR=12AC

Thus, PQ=SR and PQ∥SR

So, the quadrilateral PQRS is a parallelogram.

Similarly, in △ BCD,

Q is the midpoint of BC. (Given)

R is the midpoint of DC. (Given)

By the midpoint theorem,

QR∥BD

So, QN || LM .........(5)

LQ || MN ..........(6) (Since, PQ || AC)

From (5) and (6), we get

LMPQ is a parallelogram.

Hence, ∠ LMN= ∠ LQN (opposite angles of the parallelogram)

But, ∠ LMN= 90° (Diagonals of a rhombus are perpendicular)

So, ∠ LQN = 90°

Thus, a parallelogram whose one angle is a right angle is a rectangle. Hence, PQRS is a rectangle.

Q3 ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution:

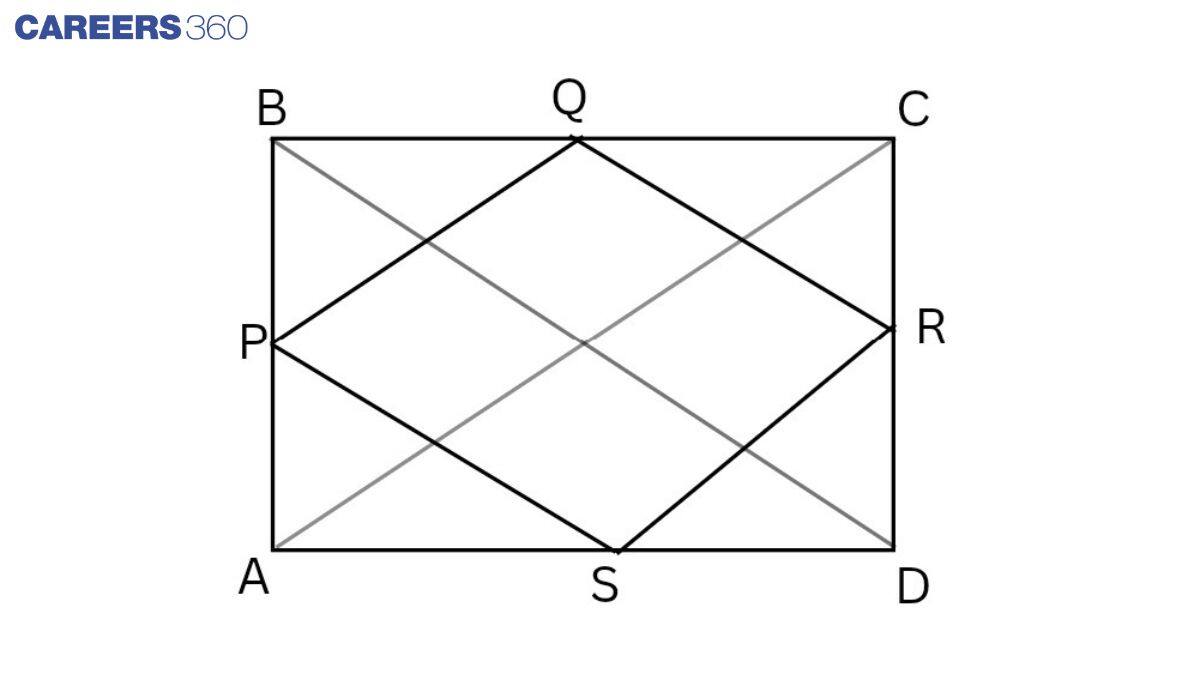
Given: ABCD is a rectangle and P, Q, R, and S are midpoints of the sides AB, BC, CD and DA, respectively.

To prove: the quadrilateral PQRS is a rhombus.

Proof:

In △ ACD,

S is the midpoint of DA. (Given)

R is the midpoint of DC. (Given)

By the midpoint theorem,

SR∥AC and SR=12AC ..........(1)

In △ ABC,

P is the midpoint of AB. (Given)

Q is the midpoint of BC. (Given)

By the midpoint theorem,

PQ∥AC and PQ=12AC ..........(2)

From (1) and (2), we get

PQ∥SR and PQ=SR=12AC

Thus, PQ=SR and PQ∥SR

So, the quadrilateral PQRS is a parallelogram.

Similarly, in △ BCD,

Q is the midpoint of BC. (Given)

R is the midpoint of DC. (Given)

By the midpoint theorem,

QR∥BD and QR=12BD ...........(3)

AC = BD........(4) (diagonals )

From (2), (3) and (4), we get

PQ = QR

Thus, a parallelogram whose adjacent sides are equal is a rhombus. Hence, PQRS is a rhombus.

Q4 ABCD is a trapezium in which AB∥DC , BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.21 ). Show that F is the mid-point of BC.

Solution:

Given: ABCD is a trapezium in which AB∥DC , BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30 ).

To prove: F is the midpoint of BC.

In △ ABD,

E is the midpoint of AD. (Given)

EG || AB (Given)

By the converse of the midpoint theorem,

G is the midpoint of BD.

In △ BCD,

G is the midpoint of BD. (Proved above)

FG || DC (Given)

By the converse of the midpoint theorem,

F is the midpoint of BC.

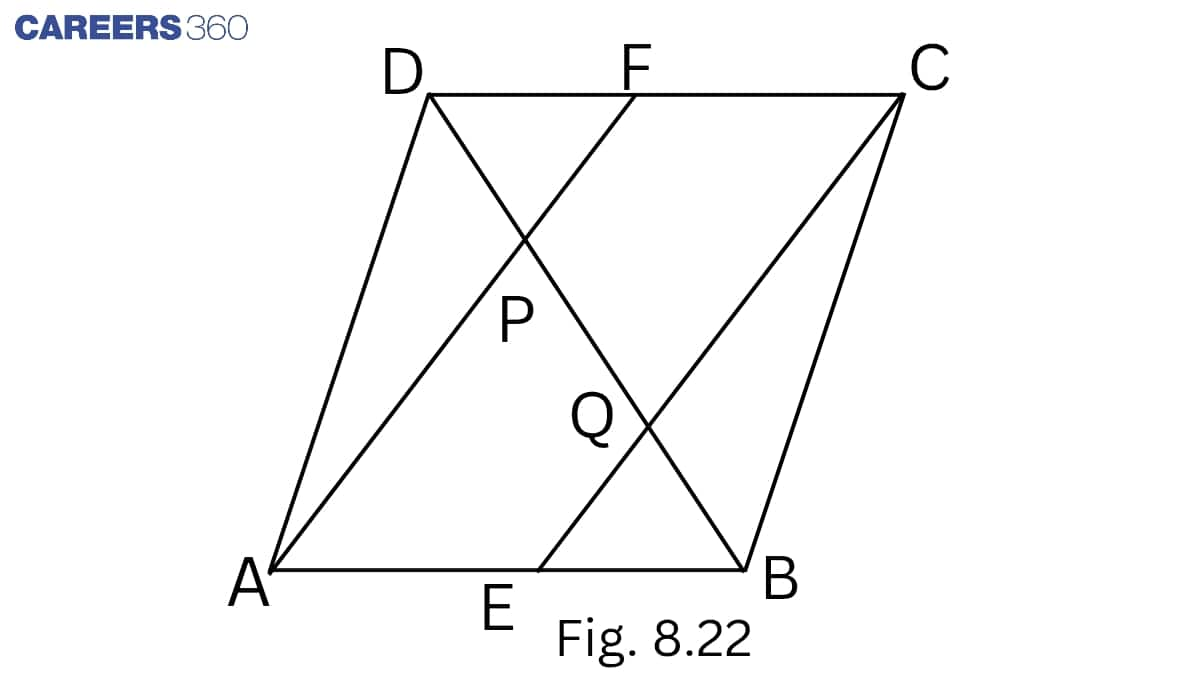
Q5 In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.22 ). Show that the line segments AF and EC trisect the diagonal BD.

Solution:

Given: In a parallelogram ABCD, E and F are the mid-points of sides AB and CD, respectively

To prove: the line segments AF and EC trisect the diagonal BD.

Proof: In quadrilateral ABCD,

AB = CD (Given)

12AB=12CD

⇒AE=CF (E and F are midpoints of AB and CD)

In quadrilateral AECF,

AE = CF (Given)

AE || CF (Opposite sides of a parallelogram)

Hence, AECF is a parallelogram.

In △ DCQ,

F is the midpoint of DC. (given )

FP || CQ (AECF is a parallelogram)

By the converse of the midpoint theorem,

P is the midpoint of DQ.

DP = PQ........(1)

In △ ABP,

E is the midpoint of AB. (given )

EQ || AP (AECF is a parallelogram)

By the converse of the midpoint theorem,

Q is the midpoint of PB.

PQ = QB........(2)

From (1) and (2), we have

DP = PQ = QB.

Hence, the line segments AF and EC trisect the diagonal BD.

Q6 (i) ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC .

Solution: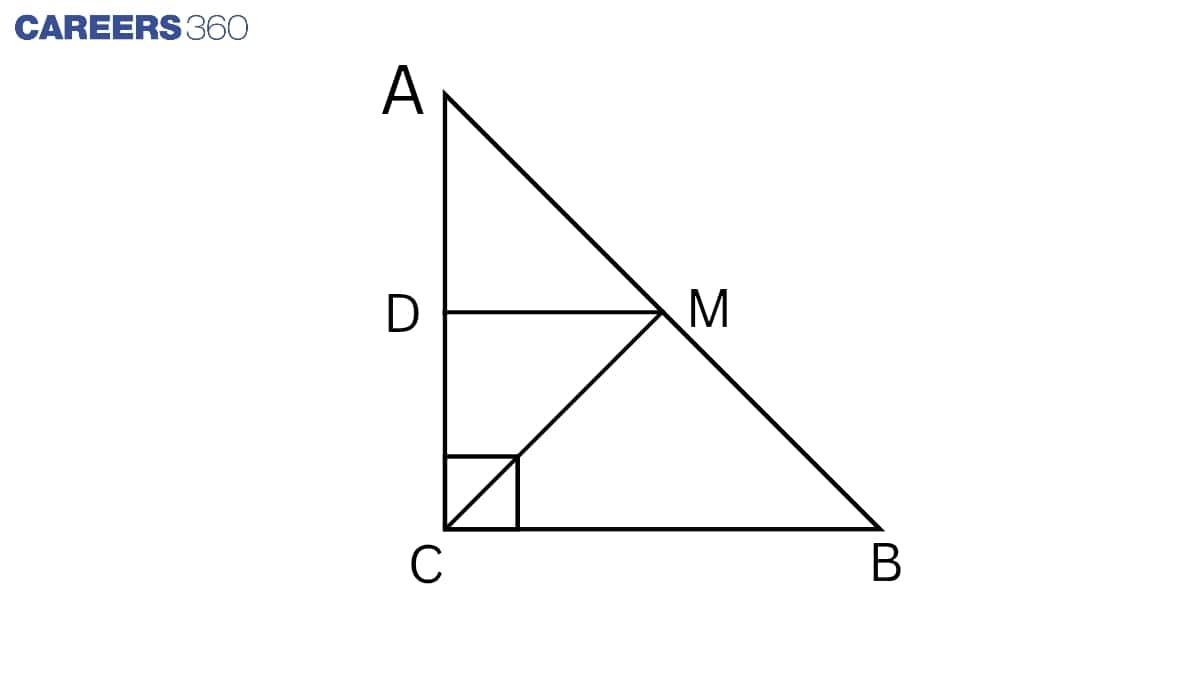

Given: ABC is a right-angled triangle right-angled at C. A line through the mid-point M of the hypotenuse AB and parallel to BC intersects AC at D.

To prove: D is the midpoint of AC.

Proof: In △ ABC,

M is the midpoint of AB. (Given)

DM || BC (Given)

By the converse of the midpoint theorem,

D is the midpoint of AC.

Q6(ii) ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC

Solution:

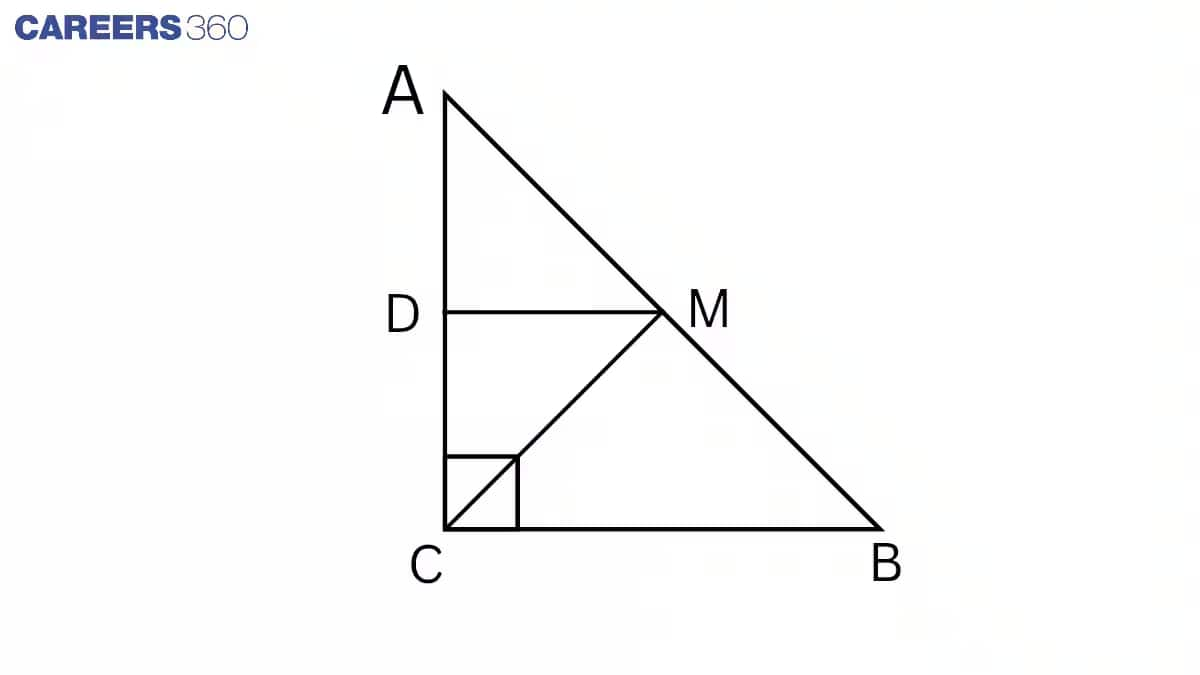
Given: ABC is a right-angled triangle right-angled at C. A line through the mid-point M of the hypotenuse AB and parallel to BC intersects AC at D.

To prove : MD⊥AC

Proof : ∠ ADM = ∠ ACB (Corresponding angles)

∠ ADM= 90∘ . ( ∠ ACB = 90∘ )

Hence, MD⊥AC .

Q6 (iii) ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM=MA=12AB

Solution:

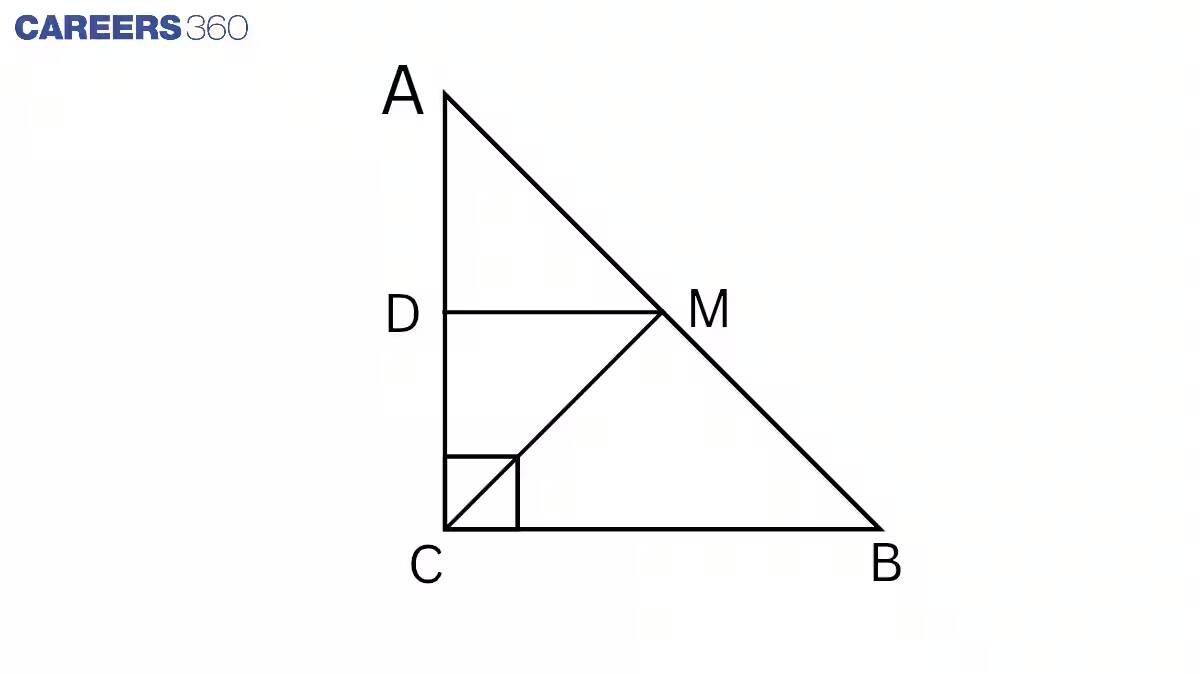
Given: ABC is a right-angled triangle right-angled at C. A line through the mid-point M of the hypotenuse AB and parallel to BC intersects AC at D.

To prove : CM=MA=12AB

Proof : In △ ABC,

M is the midpoint of AB. (Given)

DM || BC (Given)

By the converse of the midpoint theorem,

D is the midpoint of AC, i.e. AD = DC.

In △ AMD and △ CMD,

AD = DC (proved above)

∠ ADM = ∠ CDM (Each right angle)

DM = DM (Common)

△ AMD ≅ △ CMD (By SAS)

AM = CM (CPCT)

But , AM=12AB

Hence, CM=MA=12AB .

Also Read

Quadrilaterals Exercise 8.1

Topics covered in Chapter 8, Quadrilateral: Exercise 8.2

Midpoint algorithm - This algorithm defines the midpoint of the sides of the triangle. When these two midpoints join, then this line segment is parallel to the third side of the triangle. This is also applicable to the trapezium.
Properties and applications of the algorithm - Some applications are for solving for unknown sides and angles, proving parallelograms, solving problems related to triangles, etc.

Also, See

NCERT Solutions of Class 10 Subject Wise

Students must check the NCERT solutions for Class 9 Maths and Science given below:

Subject Wise NCERT Exemplar Solutions

Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:

Frequently Asked Questions (FAQs)

Q: What is the sum of all the angles of a quadrilateral and a triangle?

The sum of all the angles of a quadrilateral that has four sides is 360 and the sum of the angles of a triangle is 180 degrees. A triangle has three sides

Q: What is midpoint theorem?

The midpoint hypothesis expresses that assuming a line segment is drawn joining the midpoints of any different sides of a triangle it is parallels corresponding to the third side and is equivalent to half of the length of the third side.

Q: A line is drawn parallel to the base of a triangle passes through one of the mid-points of the side of the triangle. Find the point where it touches the third side?

It will also pass through the mid-point of the other side.

Q: A line parallel to the base passes through the mid-points of the side of triangle. What will be the area of that small triangle?

The area of the smaller triangle formed will be one-fourth of the area of the original triangle.

Q: A line parallel to the base passes through the mid-points of the side of triangle. What is the relation between the original triangle and the new smaller triangle formed?

The new smaller triangle will always be similar to the original triangle if it is formed by the line parallel to the base that passes through the mid-points of the side of the triangle.

Q: How many triangles are formed when all the diagonals are drawn inside a quadrilateral?

A total of four triangles are formed when all the diagonals are drawn inside a quadrilateral.

Q: What is the main concept of NCERT solutions for Class 9 Maths exercise 8.2?

NCERT solutions for Class 9 Maths exercise 8.2 is based mid-point theorem and its application.

Articles

IOQM Answer Key 2025: Download IOQM Solution PDF for All Sets

Sep 02, 2025

SOF IEO Sample Papers 2025-26 For Classes 1 to 12 (Free PDF)

Sep 02, 2025

IOQM Admit Card 2025: Download Indian Olympiad Qualifier in Mathematics Hall Ticket

Aug 29, 2025

Cambridge IGCSE Result 2025: Check Cambridge IGCSE Result Dates & Grading System

Aug 26, 2025

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is