NCERT Solutions for Class 7 Maths Chapter 5 Parallel and Intersecting Lines

From the railway tracks to the edges of a notebook, parallel and intersecting lines appear everywhere, all around us. In class 7, chapter 5, the students will get to know all about the lines that never meet or intersect one another, known as the parallel lines and also the lines that do intersect or meet each other, known as the intersecting lines. These basic geometric concepts are the foundation of advanced geometry, which will be taught in the higher classes. Therefore, it is essential to understand this chapter with a proper understanding and clarity, as this is where the NCERT Solutions for Class 7 Maths come into play.

This article contains comprehensive solutions for all the questions in this chapter. These NCERT Solutions provide detailed and step-by-step explanations for the students. With the help of these solutions, they can practice the problems, verify their answer and strengthen their weak areas that need improvement. This will also clear their doubts and give them a proper idea about the concepts of the chapter. Students can refer to the NCERT Solutions for Class 7 to access the subject-wise solutions of Class 7.

NCERT Solutions for Class 7 Maths Chapter 5 Parallel and Intersecting Lines Solutions (Exercise)

Figure it Out

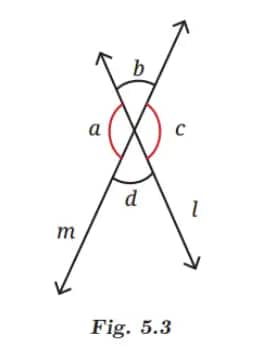
List all the linear pairs and vertically opposite angles you observe in Fig. 5.3:

Answer:

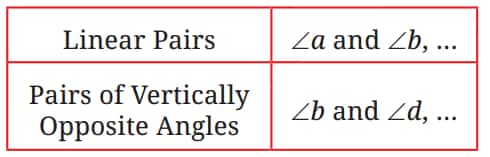
Linear pair angles: ∠a and ∠b; ∠b and ∠c; ∠c and ∠d; ∠a and ∠d.

Vertically opposite angles: ∠a and ∠c; ∠b and ∠d.

Figure it Out

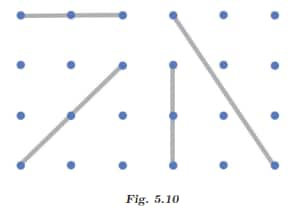
Q1: Draw some lines perpendicular to the lines given on the dot paper in Fig. 5.10.

Answer:

Draw lines that intersect the given lines at 90° angles, using a set square or protractor to ensure right angles. Do it Yourself.

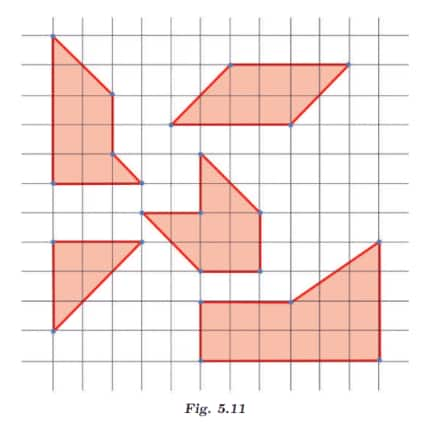
Q2: In Fig. 5.11, mark the parallel lines using the notation given above (single arrow, double arrow, etc.). Mark the angle between perpendicular lines with a square symbol.

(a) How did you spot the perpendicular lines?

(b) How did you spot the parallel lines?

Answer:

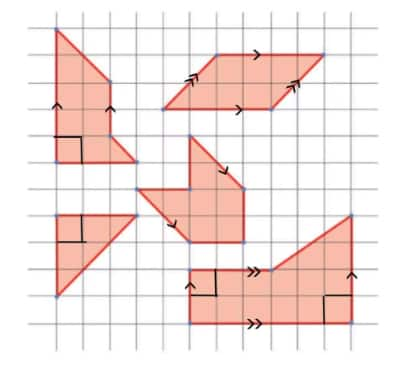
(a) Lines that intersect at a 90° angle are perpendicular.

(b) Lines that do not meet, no matter how far they are extended, are parallel.

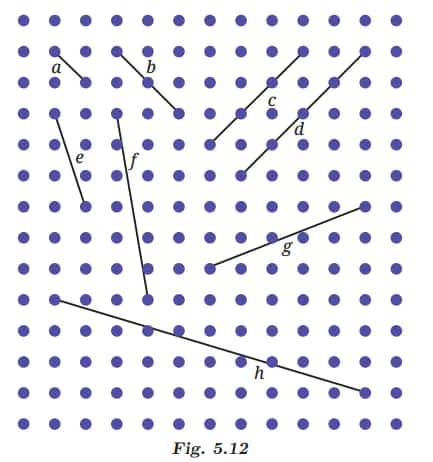
Q3: In the dot paper following, draw different sets of parallel lines. The line segments can be of different lengths but should have dots as endpoints.

Answer:

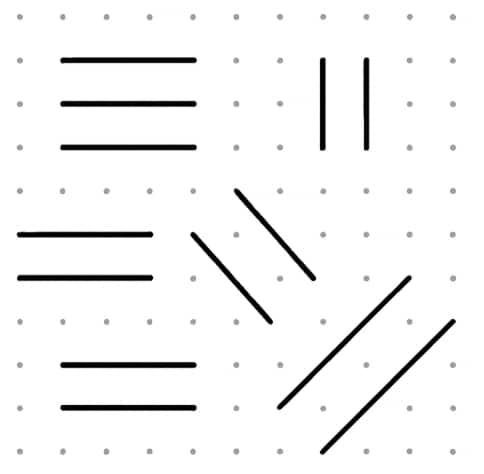
Q4: Using your sense of how parallel lines look, try to draw lines parallel to the line segments on this dot paper.

(a) Did you find it challenging to draw some of them?

(b) Which ones?

(c) How did you do it?

Answer:

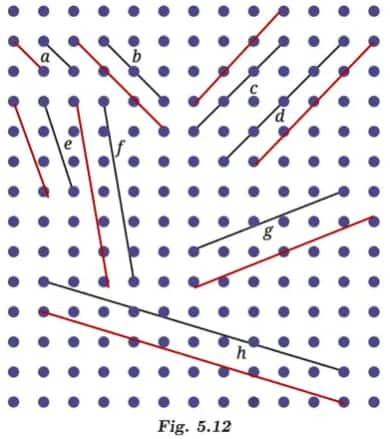
(a) Yes, some line segments are a little more difficult to draw than others.

(b) Line segments e, f, h, and g.

(c) Parallel lines are drawn by keeping them equidistant from the given lines.

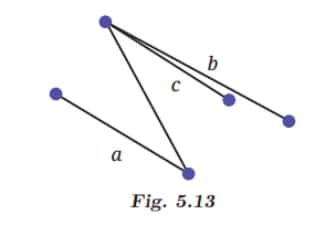
Q5: In Fig. 5.13, which line is parallel to line a – line b or line c? How do you decide this?

Answer:

In the given figure, line a is parallel to line c because these two lines are always the same distance apart and never meet, no matter how far they go.

Figure it Out

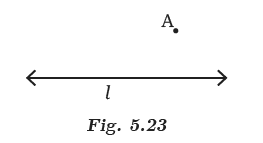
Can you draw a line parallel to l, that goes through point A? How will you do it with the tools from your geometry box? Describe your method.

Answer:

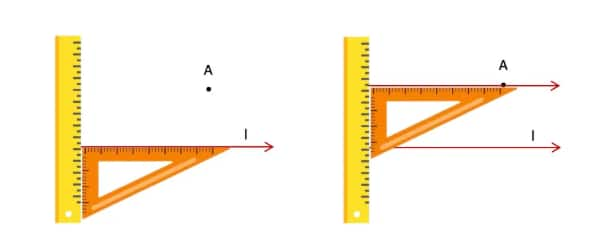
Step-by-step procedure:

• Align one edge of the set square with line l.

• Place a ruler along the other perpendicular edge.

• Slide the set square along the ruler until it reaches point A.

• Draw a line through A along the set square’s edge.

• This is the required line parallel to l.

Figure it Out

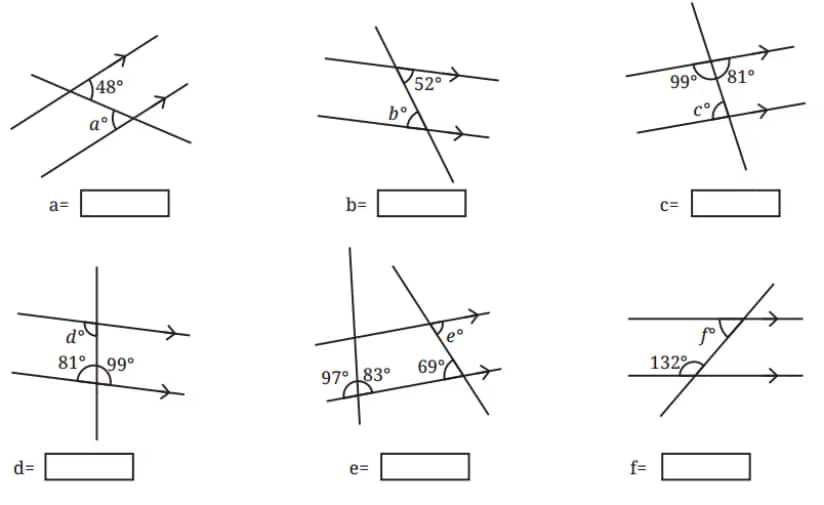
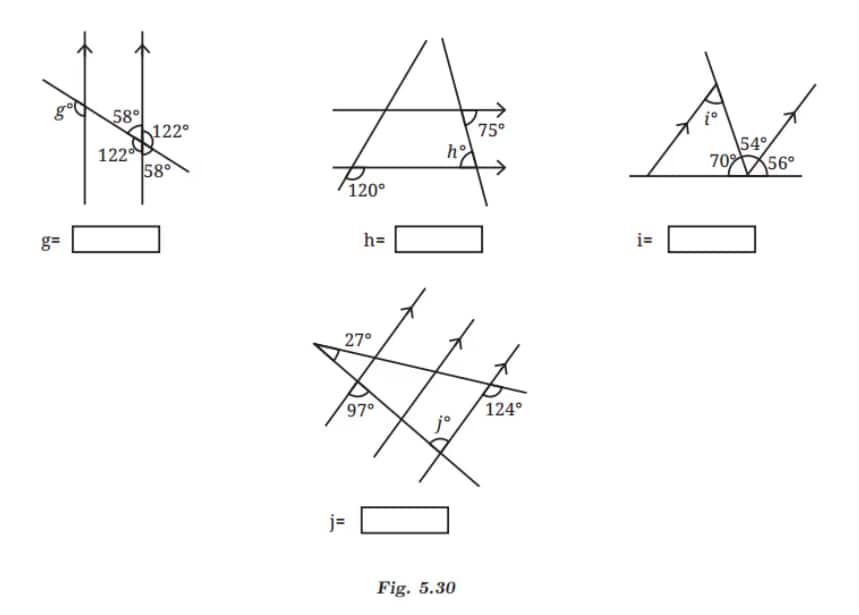
Q1: Find the angles marked below.

Answer:

(i) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠a = 48°.

(ii) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠b = 52°.

(iii) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠c = 81°.

(iv) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠d = 99°.

(v) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠e = 69°.

(vi) Since the sum of interior angles on the same side of a transversal is always equal to 180°. Therefore, ∠f + 132° = 180°
∠f = 180° – 132°
∠f = 48°.

(vii) Since corresponding angles formed by a transversal intersecting a pair of parallel sides are equal, ∠g = 122°.

(viii) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠h = 75°.

(ix) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠i = 54°.

(x) Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, ∠j = 97°.

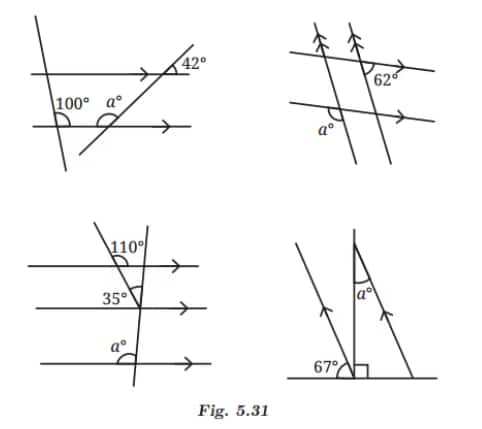
Q2: Find the angle represented by a.

Answer:

(i)

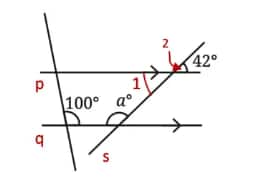
∠1 = ∠2 = 42° ……….(Vertically opposite angles)

Line p is parallel to q, and s is a transversal, then

∠a + ∠1 = 180° …………….(Sum of interior angles on the same side of the transversal)

⇒ ∠a + 42° = 180°

⇒ ∠a = 180° − 42°

⇒ ∠a = 138°

(ii)

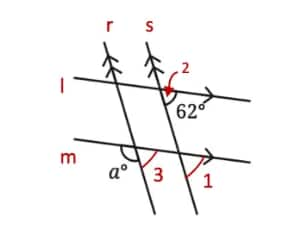
Line l is parallel to line m, and s is a transversal, then

∠1 = ∠2 = 62° ……………(Corresponding angles)

Line r is parallel to line s, and m is a transversal, then

∠1 = ∠3 = 62° ……………(Corresponding angles)

∠a + ∠3 = 180° …………..(Linear pair angles)

⇒ ∠a + 62° = 180°

⇒ ∠a = 180° − 62°

⇒ ∠a = 118°

(iii)

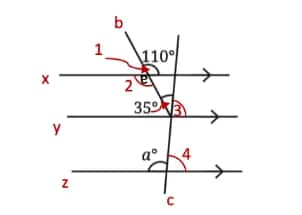
∠1 = ∠2 = 110° …… (Vertically opposite angles)

Line x is parallel to line y, and b is a transversal, then

∠2 = 35° + ∠3 ……… (Alternate interior angles)

⇒ 110° = 35° + ∠3

⇒110° – 35° = ∠3

⇒ ∠3 = 75°.

Line y is parallel to line z, and c is the transversal, then

∠3 = ∠4 = 75° ……. (Corresponding angles)

∠a + ∠4 = 180° ……… (Linear pair angles)

⇒ ∠a + 75° = 180°

⇒ ∠a = 180° – 75°

⇒ ∠a = 105°.

(iv)

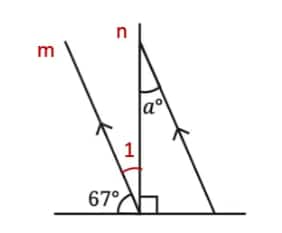
∠1 + 67° + ∠2 = 180° ……… (Sum of angles on a straight line)

⇒ ∠1 + 67° + 90° = 180°

⇒ ∠1 + 157° = 180°

⇒ ∠1 = 180° – 157°

⇒ ∠1 = 23°.

⇒ ∠1 = ∠a = 23° …… (Alternate interior angles).

Q3: In the figures below, what angles do x and y stand for?

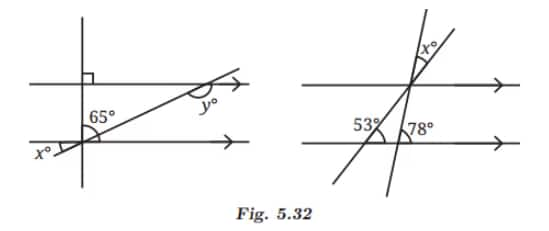
Answer:

(i)

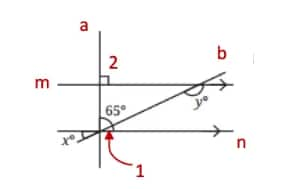
Line m is parallel to line n, and a is a transversal, then

∠2 = 65° + ∠1 ………(Corresponding angles)

⇒ 90° = 65° + ∠1

⇒ ∠1 = 90° – 65°

⇒ ∠1 = 25°.

⇒ ∠1 = x = 25° ………..(Vertically opposite angles)

Line m is parallel to line n, and b is a transversal, then

∠1 + ∠y = 180° ……………(Sum of interior angles on the same side of the transversal)

⇒ 25° + ∠y = 180°

⇒ ∠y = 180° – 25°

⇒ ∠y = 155°.

(ii)

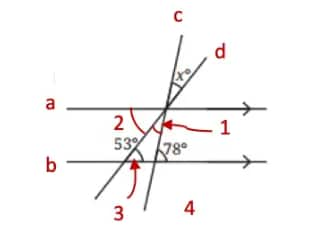
Line a is parallel to line b, and line d is a transversal, then

∠2 = ∠3 = 53° …………..(Alternate interior angles)

Also, line a is parallel to line b, and line c is a transversal, then

∠1 + ∠2 = ∠4 …………. (Alternate interior angles)

⇒ ∠1 + 53° = 78°

⇒ ∠1 = 78° – 53°

⇒ ∠1 = 25°.

Therefore, ∠1 = x = 25° ………….(Vertically opposite angles).

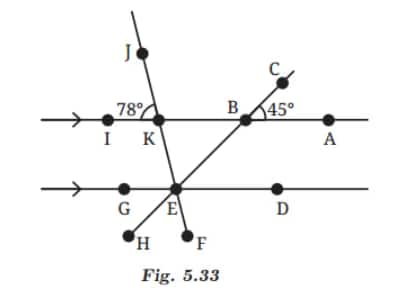
Q4: In Fig. 5.33, ∠ABC = 45° and ∠IKJ = 78°. Find angles ∠GEH, ∠HEF, and ∠FED.

Answer:

∠GEH = 45° (Exterior alternate angles)

∠FED = 78° (Exterior alternate angles)

So, ∠GEH + ∠HEF + ∠FED = 180° (all lie on a straight line)

⇒ 45° + ∠HEF + 78° = 180°

⇒ ∠HEF = 57°

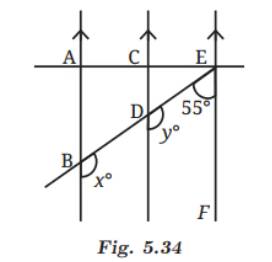
Q5: In Fig. 5.34, AB is parallel to CD, and CD is parallel to EF. Also, EA is perpendicular to AB. If ∠BEF = 55°, find the values of x and y.

Answer:

y° + 55° = 180° (Co-interior angles)

⇒ y° = 180° - 55° = 125°

Also, x° = y° ( Corresponding angles)

⇒ x° = y° = 125°.

Q6: What is the measure of angle ∠NOP in Fig. 5.35?

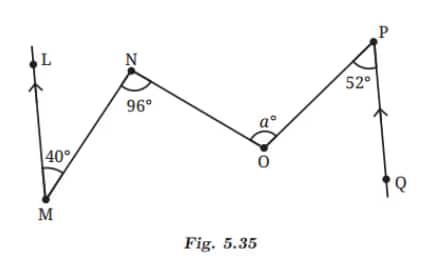
Answer:

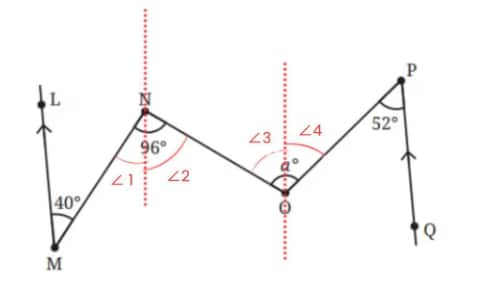
∠1 = 40° (Alternate angles are equal)

∠2 = 90° - 40° = 56°

∠3 = 56° (Alternate angles are equal)

∠4 = 52° (Alternate angles are equal)

So, ∠NOP = ∠a = 56° + 52° = 108°.

Parallel and Intersecting Lines Class 7 Maths Chapter 5 - Topics

Here, Students can find all the topics that are discussed in this chapter, Parallel and Intersecting Lines, class 7.

• Across the Line
• Perpendicular Lines
• Between Lines
• Parallel and Perpendicular Lines in Paper Folding
• Transversals
• Corresponding Angles
• Alternate Angles
• Consecutive Angle
• Parallel Illusions

NCERT Solutions for Class 7 Maths Chapter 5 Parallel and Intersecting Lines: Notes

Here are some key topics about the chapter given as notes to help the students get a clear understanding of the concepts.

Definitions

• Line: A straight path that can go infinitely in both directions.
• Line Segment: A portion of a line with two proper endpoints.
• Ray: A section of a line that starts from a point and extends indefinitely in one direction.
• Intersecting Lines: Lines which can intersect or cross one another at a point.
• Point of Intersection: The point where two lines meet each other.
• Parallel Lines: Lines that are on the same plane but never intersect with each other, regardless of how far out you draw them.
• Perpendicular Lines: Lines that meet each other and form a right angle (90°) at the point where they intersect.

Properties

• Lines that intersect each other meet at a point.
• Parallel lines never intersect and are always equidistant from each other.
• Perpendicular lines intersect each other at right angles.

Example:

• Examples of Parallel Lines are: Railway lines, lines in a notebook, and sides of a ruler.
• Examples of Intersecting Lines are: Scissors blades, crossed wires, and intersecting roads.
• Examples of Perpendicular Lines are: The corners of a square table, where walls meet the floor, and more.

Representation:

• Parallel lines are represented as: AB || CD
• Perpendicular lines are represented as: AB ⊥ CD

NCERT Solutions for Class 7 Maths Chapter 5 Parallel and Intersecting Lines - Points to Remember

Given below are some important points to remember about the chapter Parallel and Intersecting Lines:

• Every line is a straight line that extends indefinitely in both directions.
• A line segment is defined by its two endpoints.
• Lines intersect at precisely one point.
• Parallel lines never cut at any point and always remain at equal distances.
• A transversal is a line that intersects two or more lines.
• Lines that intersect create four angles at the intersection point.
• Vertically opposite angles are always congruent.
• The sum of two adjacent angles of two intersecting lines is 180°.
• If a transversal intersects two parallel lines, then it creates eight angles.

NCERT Solutions for Class 7 Maths Chapter Wise

Given below are the chapter-wise NCERT solutions for class 7 mathematics, provided in one place:

NCERT Solutions for Class 7 Subject Wise

It is very important for the students to practice the exercise questions during the exam preparation. So, the students can refer to the subject-wise solutions prepared by the subject matter experts at Careers360 using the link below.

• NCERT Solutions for Class 7 Maths
• NCERT Solutions for Class 7 Science

Also, check the NCERT Books and the NCERT Syllabus here:

• NCERT Syllabus Class 7 Maths
• NCERT Books Class 7
• NCERT Syllabus Class 7