NCERT Solutions for Class 7 Maths Chapter 14 Symmetry

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry - Download PDF

Edited By Ravindra Pindel | Updated on Feb 07, 2024 06:18 PM IST

NCERT Solutions for Maths Chapter 14 Symmetry Class 7: In mathematics, symmetry means that one shape becomes exactly like another when you move(turn, flip or slide) it in some way. In nature, tree leaves, beehives, flowers, and in the logo, symbols everywhere you can find various types of symmetrical designs. In this article, you will get CBSE NCERT class 7th maths chapter 14 solution . It is an important concept of the geometrical part used in artists, designing of jewellery or clothes, architects, car manufacturers, etc. In NCERT solutions for Class 7 Maths chapter 14 Symmetry, you will get many questions related to the order of symmetry which will give you more clarity of the concept.

Latest: NCERT Class 7 Maths: Chapterwise Important Formulas with Examples and Points

This Story also Contains

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry - Important Formulae
NCERT Solutions for Maths Chapter 14 Symmetry Class 7- Important Points
NCERT Solutions for Maths Chapter 14 Symmetry Class 7
NCERT Solutions for Maths Chapter 14 Symmetry Class 7 Exercise 14.1 Question:1 (a) Copy the figures with punched holes and find the axes of symmetry for the following:
NCERT Solutions for Class 7th Math Chapter 14 Symmetry Topic 14.3
NCERT Solutions for Class 7th Math Chapter 14 Symmetry Exercise 14.2
NCERT Solutions for Chapter 14 Maths Class 7 Symmetry Exercise 14.3
Symmetry Class 7 Maths Chapter 14-Topics

In this chapter of NCERT, there are 19 questions in three exercises. You will get detailed explanations of all these questions in CBSE NCERT solutions for Class 7 Maths chapter 14 Symmetry. You can get NCERT Solutions from Classes 6 to 12 by clicking on the above link. Here you will get NCERT Solutions for Class 7. It is advisable that you must complete the NCERT Class 7 Maths Syllabus as soon as possible and then refer to the given solutions.

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry - Important Formulae

Angle of Rotation in regular polygon = 360°/Number of sides

A half-turn = Rotation by 180°

A quarter-turn = Rotation by 90°

Reflection in the x-axis , ( X , Y ) → ( X , -Y )

Reflection in the y-axis , ( X , Y ) → ( -X , Y )

NCERT Solutions for Maths Chapter 14 Symmetry Class 7- Important Points

Line Symmetry:

If it can be divided into two identical parts by a line, there will be a line of symmetry.

Regular polygons have equal angles and equal sides so they have multiple lines of symmetry. The table given below shows the number of lines of symmetry in regular polygons.

Regular Polygons

Regular Hexagon

Regular

Pentagon

Square

Equilateral

Triangle

Number of the line of Symmetry

Angle of Rotation in regular polygon = 360°/Number of sides

Rotational Symmetry: When we rotate an object if it looks exactly the same , we say that it has rotational symmetry.

Centre of rotation: That fixed point about which object rotates.

Angles of rotation: The angle by which the object rotates.

Order of Rotational Symmetry:

The number of times an object looks exactly the same, in a complete turn

(360°) is called the order of rotational symmetry.

Some objects have only line of symmetry ( like letter E), some objects have only rotational symmetry ( like the letter S), and some have both symmetries ( like the letter H).

Formulas for Reflection:

Reflection in the x-axis , ( X , Y ) → ( X , -Y )

Reflection in the y-axis , ( X , Y ) → ( -X , Y )

Free download NCERT Solutions for Class 7 Maths Chapter 14 Symmetry PDF for CBSE Exam.

NCERT Solutions for Maths Chapter 14 Symmetry Class 7

Download PDF

NCERT Solutions for Class 7 Maths Chapter 14 Questions and Exercise

NCERT Solutions for Maths Chapter 14 Symmetry Class 7 Exercise 14.1
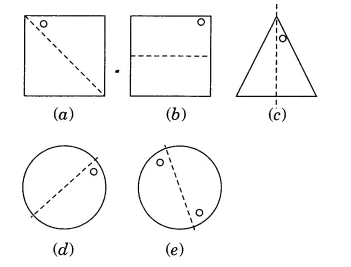
Question:1 (a) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 4656556

The axes of symmetry is as shown :

46564441

Question:1.(b) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 454454

The axes of symmetry is as shown :

1444655

Question: 1.(c) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 445465454

The axes of symmetry is as shown :

4544113215641

Question: 1.(d) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 4444145

The axes of symmetry is as shown :

445456444

Question: 1 .(e) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 4654511654

The axes of symmetry is as shown :

4444454

Question: 1 (f) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 454544546

The axes of symmetry is as shown :

445411466

Question: 1 (g) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 154454544

The axes of symmetry is as shown :

154545454545

Question: 1( h) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 114444466

The axes of symmetry are as shown :

154544444

Question: 1(i) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 15444545441

The axes of symmetry is as shown :

132323232

Question: 1(j) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 123154545

The axes of symmetry is as shown :

112121215

Question: 1.(k) Copy the figures with punched holes and find the axes of symmetry for the following:

Answer: 11545422

The axes of symmetry is as shown :

1215454544

Question:1.(l) Copy the figures with punched holes and find the axes of symmetry for the following:

4548487

Answer: 4548487

The axes of symmetry is as shown :

154544

Question: 2 Given the line(s) of symmetry, find the other hole(s):

Answer: The other holes from the symmetry are as shown :

1643868353545

Question:3 In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?

1643868450320

Answer:

The complete figures are as shown :

1643868390992

(a) square (b)triangle (c)rhombus

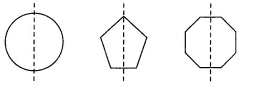
1643868391205

Question: 4 The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry

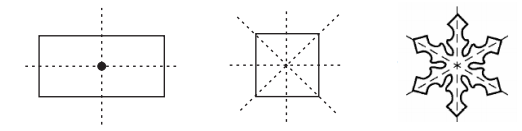
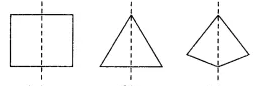
1643868544642 Identify multiple lines of symmetry, if any, in each of the following figures:

Answer:

The lines of symmetry of figures are:

(a)There are 3 lines of symmetry. Thus, it has multiple lines of symmetry.

1643868595122

(b) There are 2 lines of symmetry. Thus, it has multiple lines of symmetry.

1643868593196

(c)There are 3 lines of symmetry. Thus, it has multiple lines of symmetry.

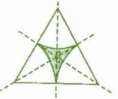
1643868594468

(d)There are 2 lines of symmetry. Thus, it has multiple lines of symmetry.

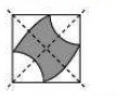
1643868593461

(e)There are 4 lines of symmetry. Thus, it has multiple lines of symmetry.

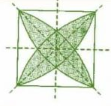
1643868594836

(f)There is 1 line of symmetry.

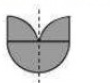
1643868592764

(g)There are 4 lines of symmetry. Thus, it has multiple lines of symmetry.

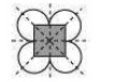
1643868593747

(h)There are 6 lines of symmetry. Thus, it has multiple lines of symmetry.

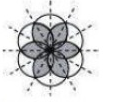
1643868594168

Question: 5 Copy the figure given here. Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?

Answer: The figure with symmetry may be as shown :

The figure with symmetry may be as shown :

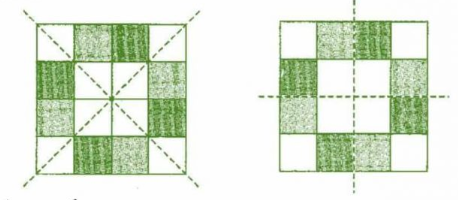
1643868628657

Yes,there more than one way .

Yes,the figure be symmetric about both the diagonals

Yes, there more than one way.

Yes,the figure be symmetric about both the diagonals

Question: 6 Copy the diagram and complete each shape to be symmetric about the mirror line(s):

Answer: The complete shape symmetric about the mirror line(s) are :

15787779

Question: 7 State the number of lines of symmetry for the following figures:

(a) An equilateral triangle (b) An isosceles triangle (c) A scalene triangle
(d) A square (e) A rectangle (f) A rhombus
(g) A parallelogram (h) A quadrilateral (i) A regular hexagon
(j) A circle

Answer:

(a) An equilateral triangle

The number of lines of symmetry = 3

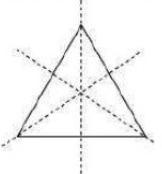
1643868681893

(b) An isosceles triangle

The number of lines of symmetry = 1

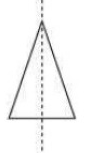
1643868679726

The number of lines of symmetry = 0

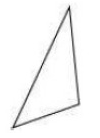
1643868680739

(d) A square

The number of lines of symmetry = 4

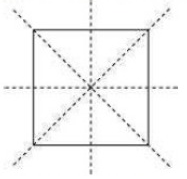
1643868682798

(e) A rectangle

The number of lines of symmetry = 2

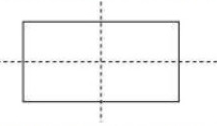
1643868680328

(f) A rhombus

The number of lines of symmetry = 2

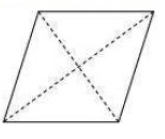
1643868681626

(g) A parallelogram

The number of lines of symmetry = 0

1643868681034

(h) A quadrilateral

The number of lines of symmetry = 0

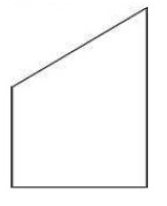
1643868681333

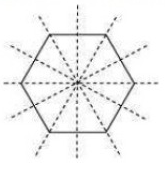
(i) A regular hexagon

The number of lines of symmetry = 6

1643868682331

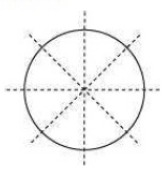
(j) A circle

The number of lines of symmetry = infinite

1643868682570

Question: 8 What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about?

(a) a vertical mirror

(b) a horizontal mirror

Answer: (a) a vertical mirror : A,H,I,M,O,T,U,V,W,X and Y

(b) horizontal mirror : B,C,D,E,H,I,O and X

Question: 9 Give three examples of shapes with no line of symmetry.

Answer: The three examples of shapes with no line of symmetry are :

1. Quadrilateral

2. Scalene triangle

3.Parallelogram

Question:10.(a) What another name can you give to the line of symmetry of an isosceles triangle?

Answer:The line of symmetry of an isosceles triangle is median or altitude.

Question: 10.(b) What other name can you give to the line of symmetry of

a circle?

Answer: The other name we can give to the line of symmetry of a circle is the diameter.

NCERT Solutions for Class 7th Math Chapter 14 Symmetry Topic 14.3

Question: 1.(a) Can you now tell the order of the rotational symmetry for an equilateral triangle?

Answer: An equilateral triangle has rotational symmetry at $120 \degree$ angle. The order of the rotational symmetry for an equilateral triangle is 3.

Question: 1.(b) How many positions are there at which the triangle looks exactly the same, when rotated about its centre by 120°?

Answer: All the triangles look same when rotated by $120 \degree$ . Thus, there are 4 positions at which the triangle looks exactly the same when rotated about its centre by 120°.

Question:2 Which of the following shapes (Fig 14.15) have rotational symmetry about the marked point.

654411544

Answer: Among the above-given shapes, (i),(ii) and (iv) have rotational symmetry about the marked point.

NCERT Solutions for Class 7th Math Chapter 14 Symmetry Exercise 14.2

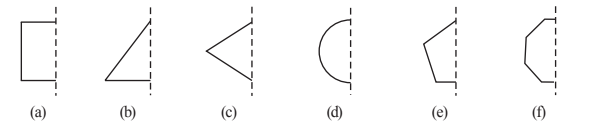
Question: 1 Which of the following figures have rotational symmetry of order more than 1:

Answer: Among the above-given shapes, (a),(b), (d),(e) and (f) have more than one rotational symmetry.

This is because, in these figures, a complete turn, more than 1 number of times, an object look exactly the same.

Question: 2 Give the order of rotational symmetry for each figure:

Answer: (a) The given figure has rotational symmetry about $180 \degree$ so it has ordered as 2.

(b) The given figure has rotational symmetry about $180 \degree$ so it has ordered as 2.

(d) The given figure has rotational symmetry about $90 \degree$ so it has ordered as 4.

(e) The given figure has rotational symmetry about $90 \degree$ so it has ordered as 4.

(f) The given figure has rotational symmetry about $72 \degree$ so it has ordered as 5.

(g) The given figure has rotational symmetry about $60 \degree$ so it has ordered as 6.

(h) The given figure has rotational symmetry about $120 \degree$ so it has ordered as 3.

NCERT Solutions for Chapter 14 Maths Class 7 Symmetry Exercise 14.3

Question: 1 Name any two figures that have both line symmetry and rotational symmetry

Answer: The two figures that have both line symmetry and rotational symmetry are :

(i) Equilateral triangle

(ii) Regular hexagon

Question:2(i) Draw, wherever possible, a rough sketch of

a triangle with both line and rotational symmetries of order more than 1.

Answer:

Line of symmetry as shown below :

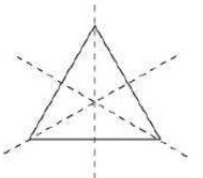
1643868736523

The rotational symmetry as shown below :

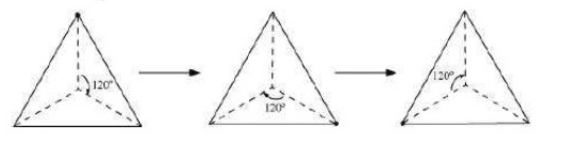
1643868736942

Question: 2(ii) Draw, wherever possible, a rough sketch of

a triangle with only line symmetry and no rotational symmetry of order more than 1.

Answer: A triangle with only line symmetry and no rotational symmetry of order more than 1 is isosceles triangle.

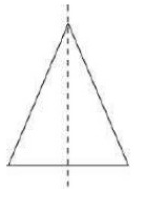
1643868755614

Question:2(iii) Draw, wherever possible, a rough sketch of

a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry

Answer: A quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry is a parallelogram.

Question: 2(iv) Draw, wherever possible, a rough sketch of

a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.

Answer: A quadrilateral with line symmetry but not a rotational symmetry of order more than 1 is kite.

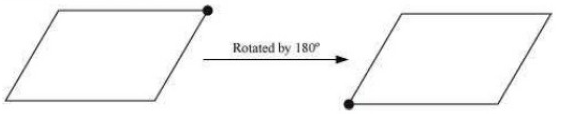
1643868803476

Question:3 If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?

Answer: Yes. If a figure has two or more lines of symmetry,than it should have rotational symmetry of order more than 1.

Question: 4 Fill in the blanks:

Shape	Centre of Rotation	Order of Rotation	Angle of Rotation
Square
Rectangle
Rhombus
Equilateral Triangle
Regular Hexagon
Circle
Semi-circle

Answer: The given table is completed as shown:

Shape	Centre of Rotation	Order of Rotation	Angle of Rotation
Square	intersection point of digonals.	4	$90 \degree$
Rectangle	Intersection point of digonals.	2	$180 \degree$
Rhombus	Intersection point of digonals.	2	$180 \degree$
Equilateral Triangle	Intersection point of medians.	3	$120 \degree$
Regular Hexagon	Intersection point of digonals.	6	$60 \degree$
Circle	centre of circle	infinite	any angle
Semi-circle	centre of circle	1	$360 \degree$

Question: 5 Name the quadrilaterals which have both line and rotational symmetry of order more than 1.

Answer:The quadrilaterals which have both line and rotational symmetry of order more than 1 are :

1. Rectangle

2. Square

3. Rhombus

Question: 6 After rotating by $60^{0}$ about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?

Answer: After rotating by $60^{0}$ about a centre, a figure looks exactly the same as its original position, then it will look symmetrical on rotating by $120 \degree,180 \degree,240 \degree,300 \degree,360 \degree.$ All angles are multiples of $60^{0}$ .

Question: 7 Can we have a rotational symmetry of order more than 1 whose angle of rotation is:

$(i)\: 45^{o}?$ $(ii)\: 17^{o}?$

Answer: We can observe that the angle of rotation is the factor of $360 \degree$ ,then it will have rotational symmetry of order more than 1.

(i) $45^{o}$ is a factor of $360 \degree$ so the figure having its angle of rotation as $45^{o}$ will have rotational symmetry of order more than 1.

(ii) $17^{o}$ is not a factor of $360 \degree$ so the figure having its angle of rotation as $17^{o}$ will not have rotational symmetry of order more than 1.

Symmetry Class 7 Maths Chapter 14-Topics

Lines of Symmetry For Regular Polygons
Rotational Symmetry
Line Symmetry And Rotational Symmetry

NCERT Solutions for Class 7 Maths Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Integers
Chapter 2	Fractions and Decimals
Chapter 3	Data Handling
Chapter 4	Simple Equations
Chapter 5	Lines and Angles
Chapter 6	The Triangle and its Properties
Chapter 7	Congruence of Triangles
Chapter 8	Comparing quantities
Chapter 9	Rational Numbers
Chapter 10	Practical Geometry
Chapter 11	Perimeter and Area
Chapter 12	Algebraic Expressions
Chapter 13	Exponents and Powers
Chapter 14	Symmetry
Chapter 15	Visualising Solid Shapes

NCERT Solutions for Class 7 Subject Wise

NCERT Solutions for Class 7 Maths

NCERT Solutions for Class 7 Science

Benefits of NCERT Solutions for Class 7th Chapter 14 Maths Symmetry

You will learn to identify different types of symmetry and also the order of the symmetry.
It will make your homework easy as you will find the detailed explanations of all the NCERT questions including practice questions given below every topic in this article.
You should try to solve all the NCERT questions including examples. If you facing difficulties in solving them, you can take help from these solutions.
After every topic, there are some practice questions given in the textbook to give you conceptual clarity. In NCERT solutions for Class 7 Maths chapter 14 Symmetry, you will find solutions to these practise questions also.

Happy learning!!!

Also Check NCERT Books and NCERT Syllabus here:

Also Read

NCERT Solutions for Class 7 Science Chapter 18 Wastewater Story

NCERT Solutions for Class 7 Science Chapter 17 Forests Our Lifeline

NCERT Solutions for Class 7 Science Chapter 16 Water A Precious Resource

NCERT Solutions for Class 7 Science Chapter 14 Electric Current and Its Effects

NCERT Solutions for Class 7 Science Chapter 13 Motion and Time

NCERT Solutions for Class 7 Science Chapter 12 Reproduction in Plants

Articles

Silverzone ABHO Result 2024-25 - Check Akhil Bhartiya Hindi Olympiad Results Here

Nov 20, 2024

Silverzone SKGKO Result 2024-25 – Check Your Scores and Performance

Nov 20, 2024

Education Loan for School Students in India – Eligibility, Benefits & Application Process

Nov 20, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Nov 20, 2024

Silverzone SKGKO Answer Key 2024-25: Download Smart Kid GK Olympiad Answer Key @ silverzone.org

Nov 20, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Nov 20, 2024

ICICI Education Loan: Eligibility, Interest Rates & Application Process

Nov 19, 2024

MPSOS 10th Result 2024 - Check MPSOS Class 10 December 2024 Exam Result @mpsos.nic.in

Nov 16, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Mock Test

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Result

Mock Test

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Admit Card

Result

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

Exam Pattern

Result

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry - Download PDF

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry - Important Formulae

NCERT Solutions for Maths Chapter 14 Symmetry Class 7- Important Points

NCERT Solutions for Maths Chapter 14 Symmetry Class 7

NCERT Solutions for Class 7 Maths Chapter 14 Questions and Exercise

NCERT Solutions for Maths Chapter 14 Symmetry Class 7 Exercise 14.1 Question:1 (a) Copy the figures with punched holes and find the axes of symmetry for the following:

NCERT Solutions for Class 7th Math Chapter 14 Symmetry Topic 14.3

NCERT Solutions for Class 7th Math Chapter 14 Symmetry Exercise 14.2

NCERT Solutions for Chapter 14 Maths Class 7 Symmetry Exercise 14.3

Symmetry Class 7 Maths Chapter 14-Topics

NCERT Solutions for Class 7 Maths Chapter Wise

NCERT Solutions for Class 7 Subject Wise

Benefits of NCERT Solutions for Class 7th Chapter 14 Maths Symmetry

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

National Institute of Open Schooling 10th examination

Mizoram Board of School Education 12th Examination

Mizoram Board 10th Examination

Punjab Board of Secondary Education 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app

NCERT Solutions for Maths Chapter 14 Symmetry Class 7 Exercise 14.1
Question:1 (a) Copy the figures with punched holes and find the axes of symmetry for the following: