NCERT Solutions For Class 8 Maths Chapter 11 Direct and Inverse Proportions
When one thing goes up, the other goes up too—or sometimes, comes down to balance it out. From sharing chocolates equally to understanding why speed reduces travel time, proportions are everywhere. You must have come across many situations where changes in one quantity result in changes in other quantities. In the world of mathematics, we say two quantities are in proportion if changes in one quantity cause corresponding changes in the other. Two quantities are in direct proportion when they increase or decrease together. It is like buying more apples will increase the total cost. While they are in inverse proportion, when one increases as the other decreases. It allows more workers to complete a job more quickly. In the NCERT Solutions for Class 8 Maths chapter 11, 'Direct and Inverse Proportions', students will learn the core concepts of proportions, along with solved examples and well-structured exercises.
This Story also Contains
- Direct and Inverse Proportions Class 8 Questions And Answers PDF Free Download
- NCERT Solutions for Class 8 Maths Chapter 11: Exercise Questions
- Direct and inverse proportions Class 8 Chapter 11: Topics
- Direct and Inverse Proportions Class 8 Solutions - Important Points
- NCERT Solutions for Class 8 Maths: Chapter Wise
Direct and inverse proportions are the scales on which life balances its give and take. You can also find solutions to these practice questions here. The main objective of these NCERT Solutions for Class 8 is to help students understand how quantities change together using direct and inverse proportions, making real-life calculations simple and logical. These Class 8 NCERT Solutions from Careers360 are designed by teachers with multiple years of experience in this field, keeping in line with the CBSE 2025-26 syllabus and exam trends. For syllabus, notes, and PDF, refer to this link: NCERT.
Direct and Inverse Proportions Class 8 Questions And Answers PDF Free Download
Students who wish to access the NCERT solutions for class 8, chapter 11, Direct and Inverse Proportions, can click on the link below to download the entire solution in PDF.
NCERT Solutions for Class 8 Maths Chapter 11: Exercise Questions
| Class 8 Maths Chapter 11 Question Answer: Exercise 11.1 Total Questions: 10 Page number: 136 |
Answer:
We say that x and y are in direct proportion, if $\frac{x}{y}=k$ or $x = ky.$
Hence in the given problem we have,
Charges for the parking:
y | x |
4 hours | Rs. 60 |
8 hours | Rs. 100 |
12 hours | Rs. 140 |
24 hours | Rs. 180 |
Considering x to be charged to be paid and y to be the parking time.
Then we calculate $\frac{x}{y}$ ,
For:- 4 hours: $\frac{60}{4}=\frac{15}{1}$ 8 hours : $\frac{100}{8}=\frac{25}{2}$
12 hours : $\frac{140}{12}=\frac{35}{3}$ 24 hours: $\frac{180}{24}=\frac{15}{2}$
Clearly, $\frac{x}{y}$ is not equal to some constant 'k', then we can say that
Parking charges are not in direct proportion to parking time.

![]()
Answer:
Suppose the parts of red pigment are x and the parts of the base are ' y '.
The requirement of the number of parts of base for 1 part of red pigment is 8,
and as the parts of red pigment increase, the parts of the base also increase in the same ratio. It is a case of direct proportion.
We can assume other parts of the base that will be required for red pigments as y1, y2, y3, and y4 for parts of pigments 4, 7, 12, and 20, respectively.

![]()
We make use of the relation of type $\frac{1}{8}=\frac{4}{y_1}$
That gives for the (i) case $y_1\times 1=8\times 4$
$⇒y_1=32$.
32 parts of the base will be required for the 4 parts of the red pigment.
(ii) If the parts of red pigment used is 7, then the parts of the base used will be
$\frac{1}{8}=\frac{7}{y_2}$
that gives $y_2\times 1=8\times 7$
$⇒y_2= 56$ .
56 parts of the base will be required for the 7 parts of the red pigment.
(iii) for 12 parts of red pigment : $\frac{1}{8}=\frac{12}{y_3}$
we have $y_3\times 1 = 8\times 12$
$⇒y_3=96$ .
So, 96 parts of the base will be required for the 12 parts of the red pigment.
(iv) for 20 parts of red pigment: $\frac{1}{8}=\frac{20}{y_4}$
we have $y_4\times 1 = 8\times 20$
$⇒y_4 = 160$ .
Hence, for the following parts of the red pigment, parts of the base are given :
Parts of the red pigment | 1 | 4 | 7 | 12 | 20 |
Parts of the base | 8 | 32 | 56 | 96 | 160 |
Answer:
As we know, the mL of red pigment is directly proportional to the mL of base.
We have to calculate for the mL of red pigment used when we mix 1800mL of base,
So, for 1 part of red pigment requires 75mL of base is required, then we
$\frac{\text{redpigment(mL)}}{\text{base(mL)}}= \frac{1}{75}$ .
So for 1800mL of the base, mL of the red pigment should be mixed
$\frac{\text{redpigment(mL)}}{1800mL}= \frac{1}{75}$
$⇒\text{redpigment(mL)}=\frac{1800}{75}=24$ mL
Hence, for the 1800 mL of base, we will mix 24 parts of red pigment.
Answer:
Given that, a machine is capable of filling 840 bottles in 6 hours. So, we can say that it is directly proportional to the time.
We can assume that bottles it will fill in five hours would be ' x '
So we got the relation; $\frac{840}{6}=\frac{x}{5}$ ,
Solving for x we will get $840\times 5 = 6\times x$
$⇒x= \frac{840\times 5}{6}= 700$ .
The machine will fill 700 bottles in 5 hours.
![]()
Answer:
We can calculate it easily,
Given that for 50,000 times enlarged, the photograph of a bacteria attains a length of 5cm.
So, we have to calculate the actual length of the bacteria(assume it to be ' x 'cm) that is when the photograph is enlarged to 1 time
Knowing that the microscope's zoom has a direct relation with the length of bacteria observed So, we get the relation ;
$\frac{50000}{1}=\frac{5}{x}$ cm
Solving the equation for x, we get;
$x=\frac{5cm}{50,000}=1\times 10^{-4}$ cm
The actual length of the bacteria is $10^{-4}$ cm, which is too small to be observed with the naked eye.
Now, calculating the length of bacteria when the photograph is enlarged 20,000 times,
Assume it as ' y '.
So, we get this relation
$\frac{20,000}{50,000}=\frac{y}{5}$
Solving for y we get;
$y=\frac{20,000\times 5cm}{50,000} = 2$ cm .
So, if the photograph is enlarged 20,000 times, only then the enlarged length would be 2 cm.

![]()
Answer:
Given that the mast of the model ship is 9 m high, while the mast of the actual ship is 12 m.
If the length of the ship given is 28m then,
Length of the model ship can be obtained from the direct proportion relation of mast height and length of ship.
We obtained the relation:
$\frac{\text { height of mast }(\text { model })}{\text { height of mast }(\text { actual })}=\frac{\text { length of ship }(\text { model })}{\text { length of ship }(\text { actual })}$
So, by the relationship we have;
Let us assume that the length of the model ship is ' x '
$\frac{9cm}{1200cm} = \frac{x}{2800cm}$ $\because$ (1m = 100cm)
After solving this relation, we get,
$x=\frac{9\times 2800}{1200}= 21$ cm,
The length of the model ship is 21cm.
Answer:
Here, given that 2 kg of sugar contains $9\times 10^6$ crystals.
So, we have to find the number of crystals in 5 kg of sugar as well as in 1.2 kg of sugar:
As here, we will assume that all crystals have the same dimensions i.e., length, breadth, and width. Then the weight of sugar follows a direct proportion with the number of crystals as increasing the number of crystals, there will be an increase in the weight also.
(i) For 5 kg of sugar:
Let the number of crystals be 'x', then,
We have the relation:
$\frac{5kg}{2kg}=\frac{x}{9\times 10^6}$ , calculating x from this relation,
$x=\frac{5kg\times 9\times 10^6}{2kg}=22.5\times 10^6$ .
Therefore, 5 kg of sugar contains $22.5\times 10^6$ sugar crystals.
(ii) For 1.2 kg sugar:
Let the number of crystals be 'y' then,
We have the relation:
$\frac{1.2kg}{2kg}=\frac{y}{9\times 10^6}$ .
Calculating similarly for y, we get
$y=5.4\times 10^6$.
Therefore, 1.2 kg of sugar contains $5.4\times 10^6$ sugar crystals.
Answer:
Given that Rashmi has a road map with a scale of 1cm representing 18km.
So we have a direct relation between scale distance and distance driven on the road.
For 72 km she drove on a road. The Distance covered in the map would be 'x' cm.
$\frac{1cm}{18km}=\frac{x}{72km}$ ,
$x=\frac{72}{18}cm$
$x=4cm$
Hence, for 72km driven on the road, we have to move a distance of 4cm on the map.
Question 9: A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time.
(i) the length of the shadow cast by another pole 10 m 50 cm high
(ii) the height of a pole that casts a shadow 5m long.
Answer:
Consider that there is a direct proportionality relation between pole height with pole shadow.
So we have a 5m 60cm high vertical pole that casts a shadow of 3m 20cm long.
(i) for the length of the shadow cast by another pole of 10 m 50cm high would be ' x ' cm;
$\frac{560cm}{320cm}=\frac{1050cm}{x}$
Finding x from the equation, we get;
$x=600cm$ .
Therefore for a 10m 50cm pole, we would get a shadow of 600cm or 6m length.
(ii) The height of a pole which casts a shadow of 5m long let it be 'y'
A similar relation holds here also, so we can apply it once more
$\frac{560cm}{320cm}=\frac{y}{500cm}$ ,
we get $y=875cm$
$y= 8m\ 75cm$.
Thus, the height of a pole that casts a shadow of 5m long is 8m 75cm.
Question 10: A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Answer:
If the speed of the truck remains the same, then we can say that the distance travelled by the truck is directly proportional to the time.
After taking 5 hours, the truck will travel a distance of let's say ' x ';
Hence, we obtain the relation:
$\begin{aligned} & \frac{14 \mathrm{~km}}{25 \text { minutes }}=\frac{x}{5 \times 60 \text { minutes }} \\ & x=\frac{14 \mathrm{~km} \times 5 \times 60 \text { minutes }}{25 \text { minutes }}=168 \mathrm{~km} ;\end{aligned}$
Thus, the truck would travel a distance of 168 km in 5 hours.
| Class 8 Maths Chapter 11 Question Answer: Exercise: 11.2 Total Questions: 11 Page number: 141-142 |
Question 1: Which of the following are in inverse proportion?
(i) The number of workers on a job and the time to complete the job.
(ii) The time taken for a journey and the distance traveled at a uniform speed.
(iii) Area of cultivated land and the crop harvested.
(iv) The time taken for a fixed journey and the speed of the vehicle.
(v) The population of a country and the area of land per person.
Answer:
(i) As the number of workers on a job increases, the time taken to complete the job decreases, hence it is an inverse proportion.
(ii) Distance and time are directly proportional to each other as time increases you could travel more distance compared to if you get less time to travel. Hence, it is not an inverse proportion.
(iii) Both the area of cultivated land and crop harvested are directly proportional, the more the area of cultivated more crop harvested. Hence it is not an inverse proportion.
(iv) With more speed if you are traveling lesser the time taken for a fixed journey to complete. Hence it is an inverse proportion.
(v) The population of a country if increases, then there would be lesser area available per person, Hence, it is an inverse proportion.
Number of winners | 1 | 2 | 4 | 5 | 8 | 10 | 20 |
Prize for each winner (in Rs.) | 1,00,000 | 50,000 | .... | .... | .... | .... | .... |
Answer:
Let us assume that the number of winners 4, 5, 8, 10, and 20 are x1, x2, x3, x4, and x5 respectively, and given that the prize money of Rs. 1,00,000 is to be divided equally amongst the winners.
Thus we have,
For 4 winners:
$\frac{Rs.1,00,000}{4}=Rs.25,000$
So Rs. 25,000 to be distributed among each.
For 5 winners:
$\frac{Rs.1,00,000}{5}=Rs.20,000$
So Rs. 20,000 be distributed among each.
For 8 winners:
$\frac{Rs.1,00,000}{8}=Rs.12,500$
So Rs. 12,500 to be distributed among each.
For 10 winners:
$\frac{Rs.1,00,000}{10}=Rs.10,000$
So Rs. 10,000 each would get.
Similarly, for 20 winners:
$\frac{Rs.1,00,000}{20}=Rs.5,000$
So Rs. 5000 each would get.
Hence, we have;
Number of winners (x) | 1 | 2 | 4 | 5 | 8 | 10 | 20 |
Prize for each winner (in ? ) (y) | 1,00,000 | 50,000 | 25,000 | 20,000 | 12,500 | 10,000 | 5,000 |
Two quantities x and y are said to be inverse proportional if they satisfy the given relation;
xy=k; where k is a constant.
Calculating xy:
$xy=1\times1,00,000=1,00,000$
$xy=2\times50,000=1,00,000$
$xy=4\times25,000=1,00,000$
$xy=5\times20,000=1,00,000$
$xy=8\times12,500=1,00,000$
$xy=10\times10,000=1,00,000$
$xy=20\times5,000=1,00,000$
We can see that the prize money given to an individual winner is inversely proportional.
![]()
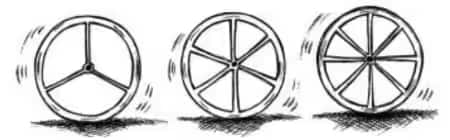
Number of spokes | 4 | 6 | 8 | 10 | 12 |
The angle between a pair of consecutive | .... | .... | .... |
Answer:
(i) Calculating the angle formed when using a different number of spokes:
The angle formed when using 8, 10, and 12 numbers of spokes a1,a2, and a3 respectively.
Hence, we have
For 8 spokes:
$\frac{360^{\circ}}{8} = 45^{\circ}$
For 10 spokes:
$\frac{360^{\circ}}{10} = 36^{\circ}$
For 12 spokes:
$\frac{360^{\circ}}{12} = 30^{\circ}$
Number of spokes (x) | 4 | 6 | 8 | 10 | 12 |
The angle between a pair of consecutive spokes (y) | 90° | 60° | 45° | 36° | 30° |
Calculating xy:
$4\times90^{\circ} = 6\times60^{\circ} = 8\times45^{\circ}=10\times36^{\circ}=12\times30^{\circ}=360^{\circ}$
Hence, we say that the number of spokes (x) and the angle formed (y) between them are in inverse proportion to each other.
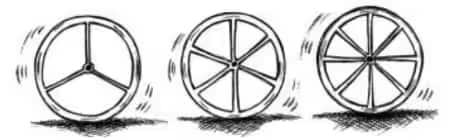
Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.
![]()
Number of spokes (x) | 4 | 6 | 8 | 10 | 12 |
The angle between a pair of consecutive spokes (y) | 90° | 60° | 45° | 36° | 30° |
Answer:
The angle between a pair of consecutive spokes on a wheel with 15 spokes is calculated as:
As we know, the constant value k = 360, then we can easily calculate the angle for 15 spokes:
$\frac{360^{\circ}}{15}=24^{\circ}$
Hence angle made is 24 degrees.
How many spokes would be needed, if the angle between a pair of consecutive spokes is $40^{\circ}$?
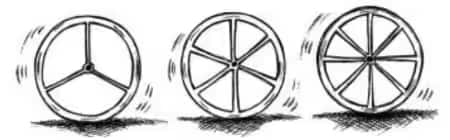
![]()
Number of spokes (x) | 4 | 6 | 8 | 10 | 12 |
The angle between a pair of consecutive spokes (y) | 90° | 60° | 45° | 36° | 30° |
Answer:
If the angle between a pair of consecutive spokes is $40^{\circ}$ then,
Number of spokes needed would be $\frac{360^{\circ}}{40^{\circ}}=9$
Hence, the required number of spokes for having 40 degrees of angle is 9
Answer:
Given that the box of sweets is divided among 24 children, getting 5 sweets each.
If the number of children is reduced by 4 then the number of children now is $24-4=20$
As here if the number of children increases then the number of sweets they will get decreases hence we can say that there exists an inverse relationship between them.
Hence,
If we assume:
Number of children before (x1) = 24
Number of sweets each would get before (y1) = 5
And the number of children after reduction (x2) = 20
And the number of sweets each would get after reduction is y2
Then the relation holds;
$x_1\times y_1=x_2\times y_2$
$24\times 5=20\times y_2$
$y_2= 6$
Hence, each child will get 6 sweets.
Answer:
The farmer has 20 animals to feed for 6 days, and after that farmer adds 10 more animals to feed, which to 20+10 = 30. So, assume that food will now long last to ' x ' days.
As the number of animals increases the required food increases but the day up to which the food will long last decreases.
Hence there exists an inverse proportion between the number of days and the number of animals.
So, we can write the relation as:
$20\times 6 = 30\times x$ or $x= 4$ days.
The food will last for about 4 days if 30 animals are there.
Answer:
Here, the situation is given that a contractor estimates that 3 persons could rewire Jasminder's house in 4 days.
Now, as the number of people increases the time they take to complete the job will decrease.
Hence, there is an inverse relationship between the number of persons and the time they took.
Jasmine now uses 4 persons instead of 3, then we can assume the time 4 persons will take be ' x '
So, we can write the relation as:
$3\times 4 = 4\times x$ days
$x= 3 $ days
Thus, the 4 people complete the job in 3 days.
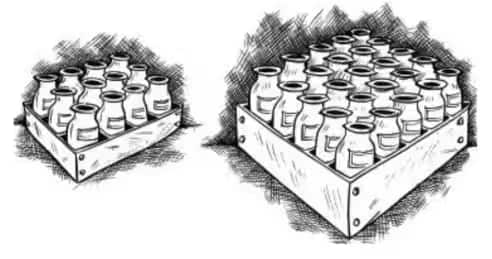
![]()
Answer:
We can easily calculate the required number of boxes to be filled, let us assume it to be 'x'
Given that a batch of bottles were packed in 25 boxes with 12 bottles in each box, Hence the total number of bottles will be $= 25\times 12 = 300$ .
So, as they produced the same number of bottles every batch and as the number of boxes increased the bottles in each box decreased
Hence, there is an inverse relation here,
$25\times 12 = 20\times x$
or $x=15$ boxes.
If the batch is packed using 20 bottles in each box then 15 boxes would be filled.
Answer:
Given that a factory requires 42 machines to produce a given number of articles in 63 days
Then we know that as the number of machines increases the time taken to produce a given number of articles decreases. Hence, there is an inverse relation here,
And let the number of machines required to produce the same number of articles in 54 days be 'x'.
Then the relation;
$42\times 63days = x\times 54days$
or $x = 49$ .
Hence, 49 machines would be required to produce the articles in 54 days.
Answer:
Given that, a car has a speed of 60 km/h, it is travelling to a destination and takes 2 hours to complete it.
Speed and time are inversely related to each other.
Assume the time it would take when travelling 80km/h be 'x'
Therefore, we can write the equation when the car travels at a speed of 80 km/h.
$2hours\times 60km/h = x\times 80km/h$
or $x= 1.5 hours$ or $1 hour\ and\ 30 minutes.$
Question 10(i): Two persons could fit new windows in a house in 3 days.
One of the people fell ill before the work started. How long would the job take now?
Answer:
Here, given that 2 persons could fit new windows in a house in 3 days.
(i) 1 person has fallen ill so, now the number of persons remaining is only one. Assume that the only person who is working takes the time of 'x' days.
Hence, we could write the inverse relation as;
$2persons\times 3 days = 1 person\times x days$
or $x= 6$ days
One person will take 6 days to complete that window job.
Question 10 (ii): Two persons could fit new windows in a house in 3 days.
How many people would be needed to fit the windows in one day?
Answer:
(ii) So, now we are calculating the number of persons that would be needed to fit the windows in one day. Let it be 'y'.
So from the previous part (I), we have the relation;
$2 persons\times 3 days = y\ persons\times 1 day$.
or $y = 6$ persons
Hence, the required number of persons would be 6.
Answer:
Given :
A school has 8 periods a day each of 45 minutes duration.
So, if the school hours of school is fixed, then there exists an inverse relationship between each period duration and the number of periods.
We can take the time of each period to be 't' if the school has 9 periods a day.
Hence, we can write the relation as;
$8\times 45 = 9\times t$
or $t = 40$ minutes
The time of each period would be 40 minutes when 9 periods are there in one day.
Direct and inverse proportions Class 8 Chapter 11: Topics
The topics discussed in the NCERT Solutions for class 8, chapter 11, Direct and inverse proportions, are:
- Introduction
- Direct Proportion
- Inverse Proportion
Direct and Inverse Proportions Class 8 Solutions - Important Points
Proportions
Proportions are represented by the symbol ∝. For example, if p is proportional to q, it's denoted as p ∝ q. If p is inversely proportional to q, it's represented as "p ∝ 1/q." In both cases, the value of 'p' changes with 'q,' or when 'q' changes, 'p' changes. The proportionality constant represents the relationship between these values, and it indicates that two ratios, such as p/q and r/s, are equivalent, i.e., p/q = r/s.
Direct Proportion or Variation
Two quantities, a and b, are in direct proportion if they change together in such a way that the ratio of their corresponding values remains constant. This is represented as a/b = k, where k is any positive number. For example, if the number of items bought increases, the total cost of purchase also increases.
Inverse Proportion
Two quantities, x and y, are in inverse proportion if an increase in x leads to a proportional decrease in y (and vice versa) in a way that the product of their corresponding values remains constant. This is represented as xy = k. For example, if the number of people increases, the time taken to finish food decreases, or if the speed increases, the time required to cover a given distance decreases.
Properties of Proportion
The important properties of proportion are:
Addendo: If $a:b=c:d$ then $a+c:b+d$
Subtrahendo: If $a:b=c:d$ then $a-c:b-d$
Dividendo: If $a:b=c:d$ then $a-b:b=c-d:d$
Componendo: If $a:b=c:d$ then $a+b:b=c+d:d$
Alternendo: If $a:b=c:d$ then $a:c=b:d$
Invertendo: If $a:b=c:d$ then $b:a=d:a$
Componendo and dividendo: If $a:b=c:d$ then $a+b:a-b=c+d:c-d$
NCERT Solutions for Class 8 Maths: Chapter Wise
For students' preparation, Careers360 has gathered all Class 8 Maths NCERT solutions here for quick and convenient access.
NCERT Solutions for Class 8 - Subject Wise
Students can find subject-wise solutions for various subjects from the links below.
NCERT Books and NCERT Syllabus
The following links will take students to the latest CBSE syllabus and some reference books.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
